《1   引言 》

1   引言 　 　

从 Yeh[1] 对水库调度优化的回顾中可以看出，不存在通用的算法，采用什么方法，取决于所考虑的水库系统的特征、可获取的数据、目标和约束条件。一般来说，可以使用的方法包括线性规划（LP）、动态规划（DP）和非线性规划（NLP）。

水库调度从本质上来说，是在一个时间段内对水库放水过程的控制，是一个动态过程问题。水库来水过程和描述水库状态的水位或蓄水量是动态变化的，根据这些客观动态变化，按水库调度的目标确定在整个调度过程中水库放水全过程的决策或控制策略。然而，上述水库调度的优化模型方法中，除动态规划外，都不能很好描述水库调度过程中的这种动态性。

动态规划方法是 Bellman （1957）为解决多阶段决策问题提出的，是一种适应于多阶段优化决策过程的方法，它在水库调度的优化中得到了广泛的应用。这是由于大部分水资源系统所具有的非线性和随机性可以转换为动态规划模型；而且，对于一个拥有众多变量的高度复杂的问题，它能够有效地将其分解为一系列可以递归求解的子问题。

动态规划方法将实际的连续过程离散为一个多阶段过程，使得问题处理起来较为方便，但是在离散过程中有可能一些重要的信息被遗漏了，它从理论上不能描述水库调度中来水变化过程、水位变化过程和放水过程的全部信息，实际上它是一种离散地描述水库调度全过程的近似动态优化方法，只适应于作为实际应用的近似计算，而不能用于确定的理论分析。其次，动态规划问题的求解大部分采用的是数值算法，从控制的角度来说，求出来的解是开环解，也就是说解只与离散时间有关，这对实际应用来说可能是方便的，但对于理论分析来说就很不方便了。如要分析参数对解的影响，只能通过变换参数在离散时间点上反复求解，才能对其有个大概近似的了解，而不能对其精确解或精确解的特性得到任何深刻的理解。造成这些问题的主要原因是动态规划只是一种适应于多阶段离散动态过程的近似描述方法，而不能精确描述连续动态变化过程的精确特性。本质上，水库调度是一个追求某个作为放水控制（决策）过程函数（常称为目标函数）的最优控制问题。由于放水控制过程作为控制决策量是时间的函数，因此水库调度追求的目标实际上是一个由水库调度中各种约束条件决定的在放水控制函数类上的泛函。虽然这种泛函描述形式对水库调度是精确的，但很少有人从这个精确描述水库调度问题的框架研究水库优化调度问题。 Massé 在 1946 年讨论了单水库水力发电的最优控制。他通过经济学推理和利用变分法的广义形式进行严格的数学推导得到了结果。 Hubert[2] 对 Massé的方法进行了简单推广，得到了一些更一般的结果。 Massé 的工作也是在连续时间的框架下进行的，由于注重经济学解释， Massé 并没有将水库调度问题描述成标准的最优控制问题，而只是将其描述成下泄流量的泛函，并给予下泄流量一个积分约束，这样的描述并不能刻画水库调度过程的动态特性。由于他采用变分法对模型进行求解，因此并未考虑对于下泄流量本身（设备能力）的约束。由此得到的是最优控制应满足的必要条件，要求出具体的解必须采用反复试算方法，也就是数值算法，因此在一定程度上也存在分析上的困难。

状态由微分方程描述的泛函极值问题更适应于用最大值原理处理和研究，因此，笔者提出了用最优控制理论描述水库调度问题和用最大值原理分析最优放水控制策略的特性和表示方式。目前有关这种方法的文献很少，而且绝大部分是利用离散的最大值原理来求解，这与精确研究水库调度的连续控制过程的特性相背离，而采用连续的最大值原理来解决水库调度问题的文献基本没有。

《2   水库调度的最优控制数学模型》

2   水库调度的最优控制数学模型 　 　

以水库供水发电多目标控制为例，水库调度是在一个时间段内根据水库运行规律对水库放水过程进行控制，以使整个时间段内的综合效益最大。水库运行规律实际上是水库蓄水量的动态变化规律，控制的放水过程是定义在时间上的、由水库调度中各种约束条件决定的一类控制函数，而综合效益是一个性能指标函数，它是前述放水控制函数的函数，即泛函。很明显，水库调度实际上是一种最优控制过程。

《2.1 状态方程》

2.1 状态方程

把水库蓄水量作为状态变量，由于水库蓄水量动态变化率是由水库的出库流量与入库流量之差决定的。因此，水库蓄水量变化规律可用以下模型描述（常称为水量平衡方程、最优控制的状态方程）：

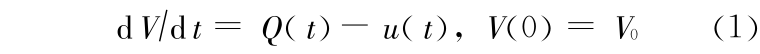
其中 V 为水库蓄水量（m3），t 为时间（s），Q（t）为水库入流（m3 /s），假定来水过程已知，且为常量。

式（1）为连续时间的微分方程，将其转换为离散时间的差分方程即为传统的水量平衡方程

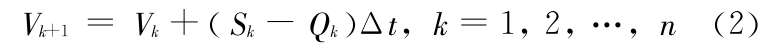
《2.2 容许控制集合》

2.2 容许控制集合

将水库下泄流量作为控制变量，一般存在以下约束：

1）航运、生态与环境约束

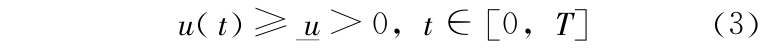
其中 u 为水库下泄流量（m3 /s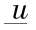）， 为满足下游航运、生态与环境所需要的最小流量，设为常量。另外，对于多泥沙河流，例如黄河，还存在为满足冲沙要求所需的最小流量。

2）水轮机最大过水量约束

其中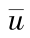 为水轮机最大过水量，这里设为常量。

3）水轮机预想出力约束

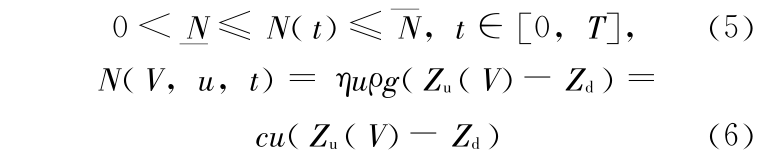
其中 N 为发电出力（kW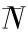）， 为水轮机预想出力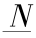， 为水轮机技术最小出力，均设为常量。ρ 为水的密度（kg/m3）， g 为重力加速度（m/s2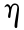）， 为发电效率及单位转换， c 为发电常数， Zu（V）为上游水位与水库蓄水量的函数关系，可由水位库容曲线求得，为已知。

因此，容许控制集合为

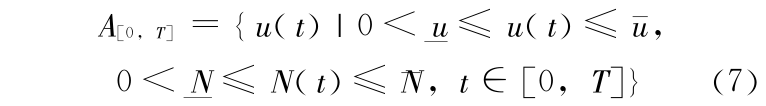
《2.3 约束条件》

2.3 约束条件

1）防洪限制约束

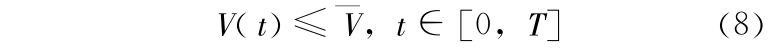
其中 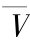为防洪限制水库蓄水的最高值，为常量。

2）灌溉、旅游、供水、养殖及野生动物保护约束

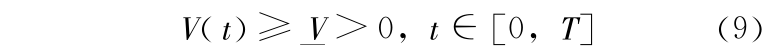
其中 为满足灌溉、旅游、供水、养殖及野生动物保护要求水库必须维持的最低蓄水量，为常量。

约束条件实质上是水库的死水位、枯水期消落水位与最高洪水位、汛期限制水位，这些都是水库调度的前提条件。实际应用中还需考虑淤积因素。

《2.4 性能指标》

2.4 性能指标

由于实际的水利水电工程大多为多目标应用，这里考虑供水和发电的综合性能指标。发电效益指标是以某一固定时间段内的发电效益最大为目标

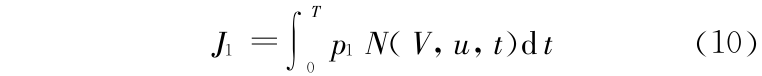
其中 J1 为发电效益（元）， T 为固定终端时间， p1 为供电价格（元/kW· h），由于目前国内供电采用电量电价，p1 为常数。

在发电效益指标的基础上考虑下游的用水需求，即最大化供水效益

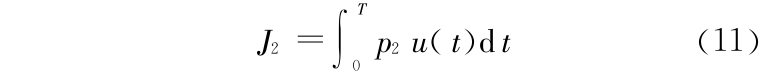
其中直接将下泄发电流量作为供水量（未考虑从水库上游引水）， p2 为单位供水量所产生的效益（元/m3 ·s-1 ），为常数。供水效益是整个过程中的供水量所产生的经济效益。

用加权法将多目标问题转变为单目标问题，即

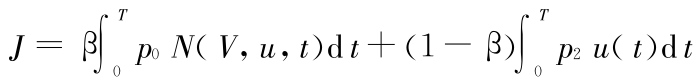
其中 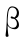∈［0，1］为权重系数，需要根据实际情况进行确定。

水库调度的最优控制数学模型为

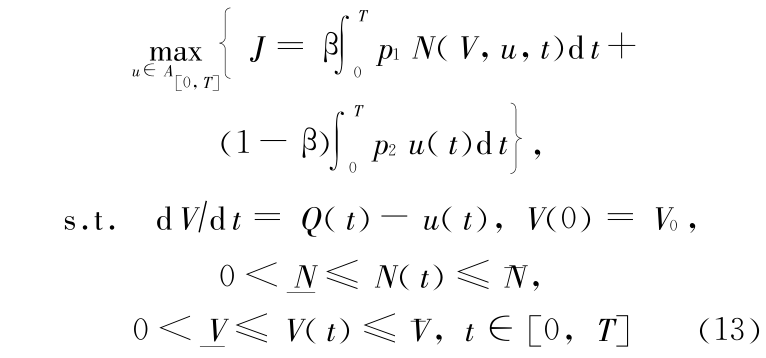
式（13）与离散时间的动态规划模型相对应，为具有状态约束与状态控制混合约束的最优控制问题。其表述为：寻求一个容许控制 u（t）∈ A［0，T］，使得式（1）在该控制作用下从初态 V（0）＝ V0 出发，且满足状态约束式（8）、式（9）和状态－控制混合约束式（5），整个过程在固定的终端时间 T 结束，且使性能指标 J 达到最大。

《3   水库调度的最优放水过程特性 》

3   水库调度的最优放水过程特性 　 　

考虑到处理问题与分析问题的方便，将式（13）模型简化为

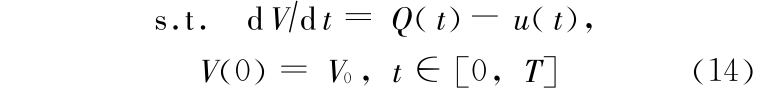
即暂不考虑将会使问题的处理大为复杂的状态约束和状态－控制混合约束，此时，

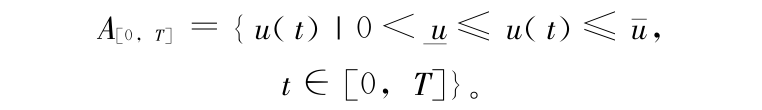
同时，考虑到变量的实际意义和便于将结果与动态规划的结果进行比较，以验证其有效性，假设 0 < 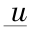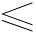Q   ，且 V0 ， T 满足（Q - ） T ＋ V0 ＞ V ，即保证水库下泄流量在整个过程中保持最大时，在终端时间水库中的存水量不会低于死库容。

利用最大值原理对其求解得：

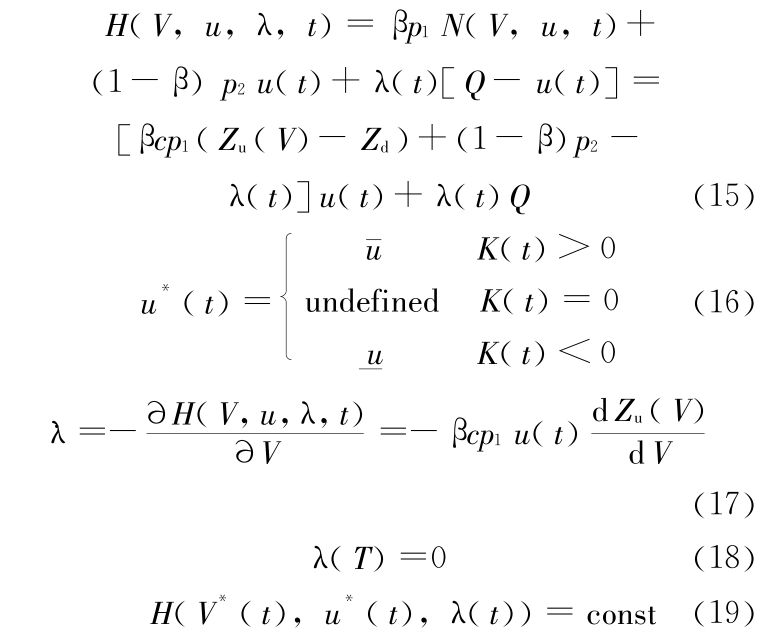
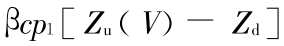
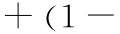
式（16）中的 K（t）＝ 称为开关函数。由于 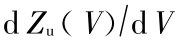＞ 0 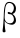，＞ 0 ，c ＞ 0 ，p1 > 0 ， u ＞ 0 ，故由式（17）知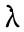＜ 0 ，结合式（18）便得到

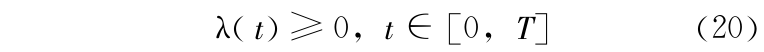
对于由状态方程及其初值与式（17）、式（18）组成的两点边值问题，通常不容易求得解析解，而需用数值方法求解。为了能够得到具体的结果，仅对 Zu（V）为一次函数的情形进行分析。

设 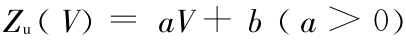，式（15）和式（17）变为

此时 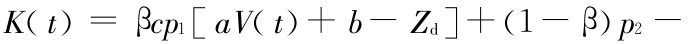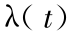，将其对时间求导得

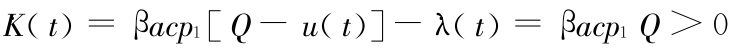
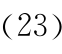
即 K（t）为一严格单调增函数。

由于 K（t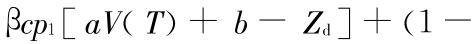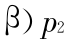）＝ 及 Zu（V）＞ Zd ，故 K（T）＞ 0 。对于 K（0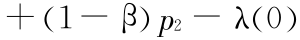）＝，并不能确定其符号，对其分两种情况讨论，结论以命题形式给出。

命题 1   在满足 K（0） 0 即

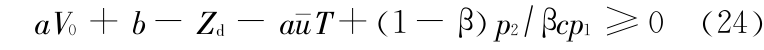
及前述假设的条件下，要使综合效益最大，水库的下泄流量在整个过程中保持最大，此时水库蓄水量随时间不断减小直至 V *（T），其变化率为 Q - 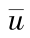，水库上游水位逐渐降低直至 Zd（V *（T））。

控制与状态变量的变化趋势如图 1 所示。

《图 1》

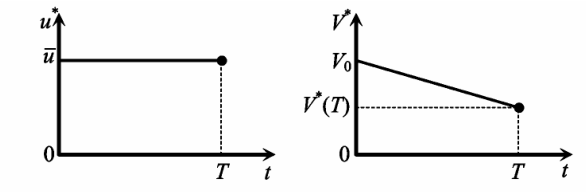
图 1 控制变量与状态变量

Fig.1 Control variable and state variable

式（24）中 Zu（V0）- Zd 为初始的发电水头，即初始时刻水库的上游水位与下游水位之差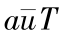； 是在整个过程中保持下泄量最大所得到的放水量造成的上游水位变化量，则式（24）表示在整个过程中保持下泄量最大所得到的放水量造成的上游水位变化量与初始时刻的发电水头之差小于一个常量  。

此时综合效益为

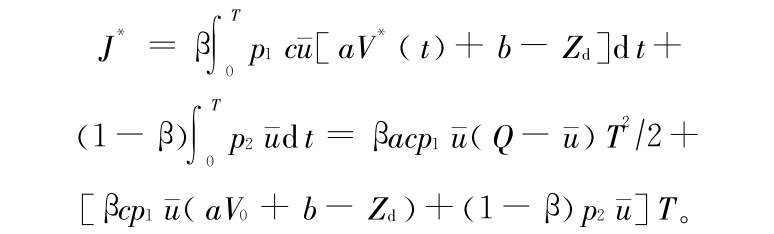
命题 2 　在满足 K（0）＜ 0 即

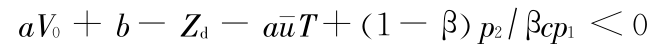
及前述假设的条件下，要使综合效益最大，则在整个过程的［0，tc）阶段，水库下泄流量保持为最小，水库蓄水量逐渐增大直至 V *（tc），水库上游水位逐渐增高直至 Zd（V *（tc）））；在［tc，T］阶段，水库下泄流量保持为最大，水库蓄水量逐渐减小直至 V *（T），水库上游水位逐渐降低直至 Zd（V *（T））。控制与状态变量的变化趋势如图 2 所示。

命题２中的转换时间为

《图 2》

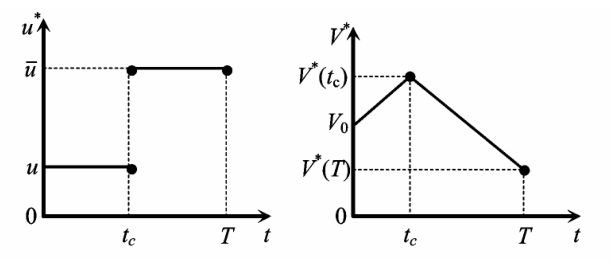
图 2 控制变量与状态变量

Fig.2 Control variable and state variable

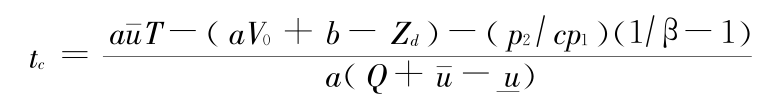
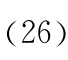
与前一种情况类似，式（25）表示，在整个过程中保持下泄流量为最大所得到的放水量造成的上游水位的变化量与初始时刻发电水头之差小于一个常量 。同时，从式（26）可以看到，只有满足式（25），tc 才大于零。此时综合效益为

《4   分析 》

4   分析 　 　

1）对于命题 1 的第一种情况，最优控制对于发电和供水而言都是最优的。对命题 2 的第二种情况，显示出发电与供水之间的矛盾。从供水的角度来说，希望在整个过程中保持下泄流量为最大，但这样就损失了一部分发电效益。此时的最优控制利用决策者对两个目标赋予的权重系数来解决矛盾，见式（26）。当 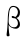减小，1 - 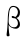增大，即决策者对供水效益的重视程度增加时，tc 减小，下泄流量保持最高的时长增加，供水效益增加，而发电效益减少。

2）通过以上模型求解过程可以看到，得到的最优控制为 bang-bang 控制，造成这种结果的原因主要是： a . 目标函数及 Hamilton 函数是关于 u 的线性函数； b. u 受到不等式约束 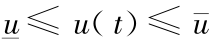。这种 bang-bang 控制的形式与实际生产中的情况有些差异，造成差异的根源主要有两个：假设来水为常量；未考虑状态约束和状态－控制混合约束。

3）在 3 节中为了分析处理的方便，要求参数满足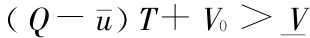 。现假设除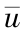增大外，其余参数均不变，考虑到实际的水库调度过程，要在水量平衡约束与水库下泄流量约束下（未考虑其他约束），控制水库下泄流量，使得水库从起始库容 V0 开始，在终端时间 T 达到要求状态（比如死库容 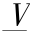），从而使得在整个周期［0，T］内的发电量最大，因此，可以认为此时相当于求解最优控制问题：

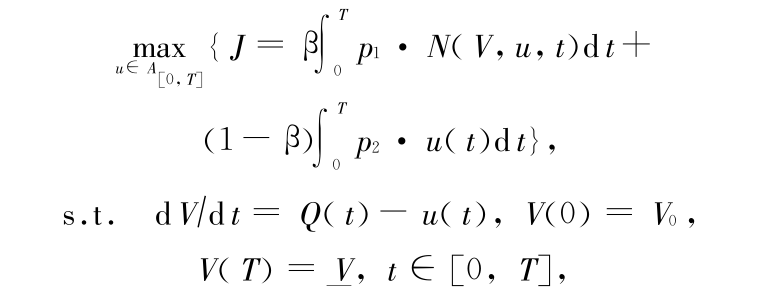
其中 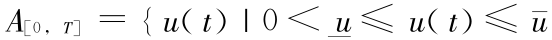，t ∈［0，T］｝，0 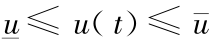＜ 。通过与第 3 节类似的分析，可以求得：

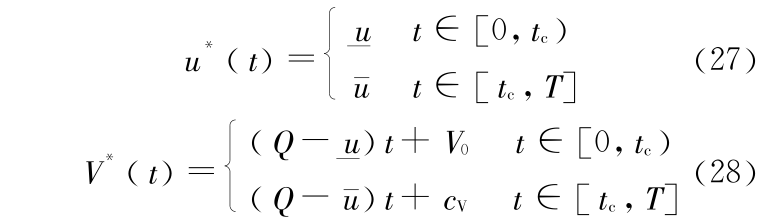
其中 tc 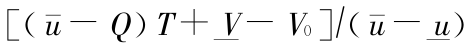＝，cV 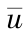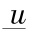＝（ －） tc + V0 。可以看到，要使 tc 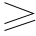0 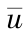， 必须满足（ Q - 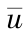） T ＋ V0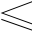 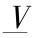，即若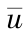 不满足此条件就回到了命题１的情况。在满足此条件的前提下，情况与命题 2 的情况类似，求解最优控制策略的关键在于确定 tc 。由于 ＞ 0 ，故 tc 随着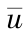 增大而增大，当 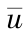→＋∞时，tc → T 。

《5   算例 》

5   算例 　 　

针对某大型水电站水库，其相应参数分别为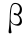： = 0.7 ，p1 = 0.35 ，p2 ＝ 0.95 ，c = 8.5 ， = 2.354 7 × 10-8 ，b = 540.907 4 ，Zd = 503.6 m ，正常蓄水位为 588 m ，死水位为 558 m ， Q = 322 m3 /s 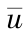， = 956 m3 /s 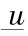， = 213 m3 /s ，考虑到前述的假设要求，将规划周期设为 20 d ，即 T = 480 h ，起调水位为 586 m 。运用动态规划对其进行求解得到 u *（t）＝ 956 m3 /s ，V *（t）＝（Q - 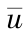） t ＋ V0 ，最优综合效益为5.372 3 × 108 元。用提出的方法进行求解，得到了与动态规划相同的结果，如图 3 所示。

《图 3》

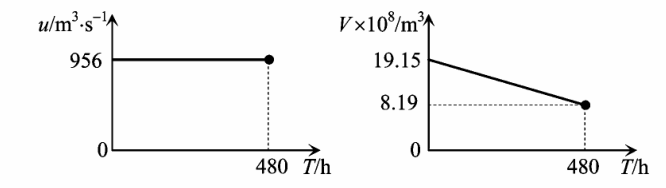
图 3 水库蓄水量和水库下泄流量

Fig.3 V *（t） and u（t）

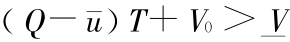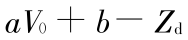
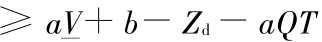
由于假设参数满足 ，对其进行变换后可得到 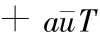，而对于一般的大型水电站水库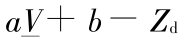， ＞ ，即满足条件式（24），此时的解为命题 1 的情况，与动态规划的结果相同。该模型并未显式地考虑状态约束，为了分析问题的方便，对参数的取值范围进行了约束，实际上起到了与状态约束类似的效果。此算例虽然简单，却足以验证所提出的方法有效性。

《6   结论 》

6   结论 　 　

用最优控制理论描述的水库调度模型，精确地描述了水库调度的连续动态变化过程。在对典型的水库调度最优控制数学模型进行一定程度地简化后，利用最大值原理得到了最优控制的特性与表示形式，进一步得到了状态的演变过程，为水库调度的进一步分析打好了基础。针对算例，将其与动态规划的结果进行了对比，验证了方法的有效性。下一步需要进行的工作包括利用最大值原理对包含状态约束的模型进行求解，并考虑来水非常量的情形。