Model of Fuzzy Geometric Programming in Economical Power Supply Radius and Optimum Seeking Method

Abstract

The choice of power supply radius for transformer substations is a complicated problem. A fuzzy geometric programming model of power supply radius under the fuzzy environment, including problems of soft constraints and fuzzy functions with fuzzy coefficients, is built in order to determine the best choice with less investment and lower energy loss. From the model built in this paper more information can be collected and more satisfactory results can be obtained compared with other static and dynamic optimum mathematical models such as controlling models and classical geometric programming ones.

Content

《1 引言》

1 引言

随着我国电力事业的大发展, 变电所供电半径的优选, 是一个有实际价值的问题。目前, 已建立了静态和动态的优化数学模型^[1,2]。但是, 供电半径在复杂的实际环境下选择将更加困难。为了使所建立的模型包含的信息量更大, 适应面更广, 利用Fuzzy集的理论, 将1987年提出的Fuzzy几何规划应用于变电所经济供电半径的优选。它比经典模型的结果有更准确、应用更广泛等特点。

《2 Fuzzy几何规划模型的建立》

2 Fuzzy几何规划模型的建立

考虑城市110 kV变电所直接降压为10 kV向用户供电, 采用年费用法建立模型。设^[1]:

1) 供电范围是以110 kV变电所为中心, R为半径的圆内, 且10 kV配电网为辐射形结构;

2) 不考虑投资过程, 投资费用是在一定负荷水平下发生的年运行费μ;

3) 投资回收期确定为抵偿年限N (8～10年) , 即总投资在抵偿年限内回收。

4) 整个电网覆盖面上负荷密度均匀。

于是, 用年费用法建立的静态模型如下:

$F = Ζ / Ν + μ,$ $F = Ζ / Ν + μ,$

其中, F为年费用, Z为总投资费用。

单位容量的年费用函数可表示为

$\begin{array}{l} F_{0} = F / S = \\ [(Ζ_{b} + Ζ_{1}) / Ν + μ_{1} + μ_{2} + μ_{3}] / S, (1) \end{array}$ $\begin{array}{l} F_{0} = F / S = \\ [(Ζ_{b} + Ζ_{1}) / Ν + μ_{1} + μ_{2} + μ_{3}] / S, (1) \end{array}$

根据文献[2], 有:

$Ζ_{b} = a_{1} + b_{1} S (2)$ $Ζ_{b} = a_{1} + b_{1} S (2)$

为110 kV变电所建设投资费。

$Ζ_{1} = L (Μ a_{2} + b_{2} S_{1}) (3)$ $Ζ_{1} = L (Μ a_{2} + b_{2} S_{1}) (3)$

为10 kV中压配电网主干线建设投资费。其中:M=Scosφ /P_av为10kV中压配电网出线回路数, L=ER (km) 为10 kV中压配电网出线每回路线路长度, E为地形修正系数, S_l为110 kV变电所全部的10 kV中压配电网主干线导线总截面积 (mm²) , l是导线的长度 (km) 。

$μ_{1} = Η (Ζ_{b} + Ζ_{1}) (4)$ $μ_{1} = Η (Ζ_{b} + Ζ_{1}) (4)$

为110 kV变电所和10 kV中压配电网线路的运行费用的不变部分 (大修、小修、折旧费) 与总投资的正比例函数。

$μ_{2} = Δ Ρ τ C_{0} = 7.26 \frac{E ρ J τ C_{0}}{U_{Ν} \cos^{2} φ \sqrt{σ}} S^{3 / 2} 10^{- 5} (5)$ $μ_{2} = Δ Ρ τ C_{0} = 7.26 \frac{E ρ J τ C_{0}}{U_{Ν} \cos^{2} φ \sqrt{σ}} S^{3 / 2} 10^{- 5} (5)$

为全年10 kV线路损失费。

而110 kV变电所变压器的损失费用为^[3]:

$μ_{3} = (8760 C_{0} Κ_{F e} + C_{0} τ_{b} Κ_{c u}) γ S_{Ν L}^{3 / 4} ‚ (6)$ $μ_{3} = (8760 C_{0} Κ_{F e} + C_{0} τ_{b} Κ_{c u}) γ S_{Ν L}^{3 / 4} ‚ (6)$

其中, γ为变压器的台数。

将式 (2) ～ (6) 代入式 (1) , 得

$\begin{array}{l} F_{0} = (\frac{1}{Ν} + Η) (\frac{a_{1}}{S} + b_{1}) + E [\sqrt{\frac{S}{π σ Κ_{c}}} \cdot \\ (\frac{a_{2} \cos φ}{Ρ_{a v}} + \frac{b_{2}}{\sqrt{3} U_{Ν} J}) + 7.26 \frac{ρ J τ C_{0}}{U_{Ν} \cos^{2} φ} \frac{10^{- 5}}{\sqrt{σ}}] S^{1 / 2} + \\ (8760 C_{0} Κ_{F e} + C_{0} τ_{b} Κ_{c u}) \frac{S_{Ν L}^{3 / 4}}{S_{Ν}} 。 (7) \end{array}$ $\begin{array}{l} F_{0} = (\frac{1}{Ν} + Η) (\frac{a_{1}}{S} + b_{1}) + E [\sqrt{\frac{S}{π σ Κ_{c}}} \cdot \\ (\frac{a_{2} \cos φ}{Ρ_{a v}} + \frac{b_{2}}{\sqrt{3} U_{Ν} J}) + 7.26 \frac{ρ J τ C_{0}}{U_{Ν} \cos^{2} φ} \frac{10^{- 5}}{\sqrt{σ}}] S^{1 / 2} + \\ (8760 C_{0} Κ_{F e} + C_{0} τ_{b} Κ_{c u}) \frac{S_{Ν L}^{3 / 4}}{S_{Ν}} 。 (7) \end{array}$

式中:H为对总投资提取的年运行费的年提取系数;S为变电所容量 (kVA) ;a₁为投资中与变电所容量无关部分的系数 (元) ;a₂为10 kV线路投资中与导线截面无关的每公里的投资 (元/km) ;b₁为投资中与变电所容量有关部分的系数 (元/kVA) ;b₂为10 kV线路投资中与导线截面有关部分的系数 (元/km·mm²) ;σ为平均负荷密度 (kW/km²) ;K_c为容截比 (110 kV变电所宜取2.2～2.5) ; P_av为每一回路线路平均负荷 (kW) ;U_N为中压配电网额定电压 (本文为10 kV) ;J为导线经济电流密度 (A/mm²) ;ρ为导线电阻率 (Ω·mm²/km) ;τ为年平均最大负荷损耗小时数;C₀为损耗电度成本电费 (元/kW·h) ;K_Fe为变压器的铁损系数 (≈0.0085 kW/ (kVA) ^3/4) ;τ_b为变压器的铜损耗等值小时数;K_cu为变压器的铜损系数 (≈0.055 kW/ (kVA) ^3/4) ;S_NL为每台变压器的额定负荷 (kVA) ;S_N为每台变压器额定容量 (kVA) ;静态模型的目标函数确定为单位容量的年费用最小, 即min F₀ 。

由于负荷、投资过程和电价等因素是不确定的, 含有大量的随机现象和模糊现象。然而, 经典的模型忽略这些重要的现象, 这会使模型失真, 且其适应性将受到很大的限制。这里将目标函数F₀作模糊化处理, 使单位容量的年费用模糊最小, 即

《图1》

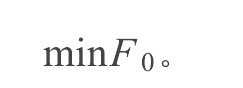
但变电所的容量是非负的, 即S>0。F₀是关于S的指数多项式函数^[4], 因此, 问题可转化为在容量S>0的约束下求年费用模糊最小, 其模型为

《图2》

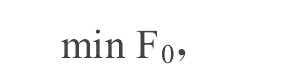
《图3》

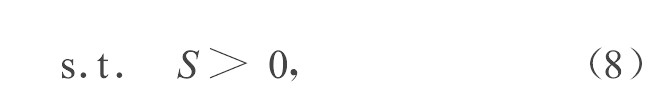
即为Fuzzy正项几何规划模型。其中目标函数F₀的系数既可为普通正实数, 也可为在某一区间内变化的正Fuzzy数。

求解式 (8) , 获得其Fuzzy最优解^[4,5,6]后, 再利用公式

$\begin{array}{l} R = \sqrt{\frac{S}{π σ Κ_{c}}}, (9) \\ n_{b} = \frac{1}{π R^{2}} = \frac{Ν_{b}}{Q}, (10) \\ Ν_{b} = \frac{Q}{π R^{2}}, (11) \end{array}$ $\begin{array}{l} R = \sqrt{\frac{S}{π σ Κ_{c}}}, (9) \\ n_{b} = \frac{1}{π R^{2}} = \frac{Ν_{b}}{Q}, (10) \\ Ν_{b} = \frac{Q}{π R^{2}}, (11) \end{array}$

获得变电所平均供电半径R, 单位面积上变电所的个数n_b和变电所的平均个数N_b。这里Q为城市电网供电区域面积 (km²) 。

《3 模型的求解》

3 模型的求解

对于Fuzzy几何规划模型式 (8) , 已有多种解法^[4,5,7], 以下用数值实例来介绍其中两种解法。为简便计算, 取一组参数值如下:

N=10, cosφ=0.9, τ =2 400 h, E =1.3, C₀ = 0.06元/ kW·h, H = 8.0 %, ρ =31.5 Ω·mm²/km, U_N=10 kV, J =1.15 A/mm², a₁=510 000元, b₁=50元/ kVA, a₂ = 18 640元/ km, b₂ = 89元 / km·mm², P_av=4 000 kW, K_c = 2.2, Q = 49.03 km², K_Fe =0.008 5 kW/ (kVA) ^3/4, K_cu= 0.055 kW (kVA) ^3/4。

将它们代入式 (1) , 便得

$F_{0} = 91 800 S^{- 1} + 0.77 S^{1 / 2} σ^{- 1 / 2},$ $F_{0} = 91 800 S^{- 1} + 0.77 S^{1 / 2} σ^{- 1 / 2},$

代入式 (8) , 即为

《图4》

由于误差, 例如变电所和中压配电线的投资费用系数的波动及电价随时间变化的影响等因素, 目标函数具有一定的伸缩性。而σ是一个参变数, 单位为kW/km², 经测定宜取:1 566.3, 3 234.9, 4 877.6, 5 915, 8 300, 11 044。

本文取定参数σ=5 915 kW/km², 且以式 (12) 为例来讨论它的两种情形的求解:模型Ⅰ, 目标函数在某允许域内伸缩;模型Ⅱ, 目标函数的系数在某一区间内波动。

称

$D = J - m - 1 = \sum_{i} J_{i} - m - 1$ $D = J - m - 1 = \sum_{i} J_{i} - m - 1$

为原几何规划及其对偶规划的困难度^[5]。其中, J为原几何规划的项数, m是变量的个数。

《3.1模型Ⅰ》

3.1模型Ⅰ

规划模型为

《图5》

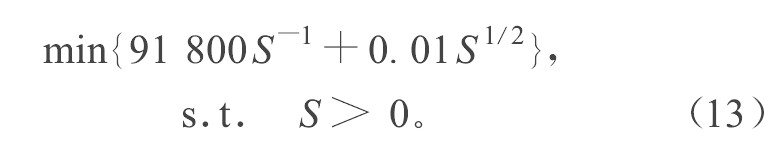
求解式 (13) , 此等价于解三个确定性几何规划, 其求解步骤^[5,6]归纳如下:

1) 解确定性几何规划

$\begin{array}{l} \min {91 800 S^{- 1} + 0.01 S^{1 / 2}}, \\ s . t . S > 0 。 (14) \end{array}$ $\begin{array}{l} \min {91 800 S^{- 1} + 0.01 S^{1 / 2}}, \\ s . t . S > 0 。 (14) \end{array}$

它的对偶规划为

$\begin{array}{l} \max d = \max (\frac{91 800}{w_{1}})^{w_{1}} (\frac{0.01}{w_{2}})^{w_{2}}, \\ s . t . w_{1} + w_{2} = 1, - w_{1} + w_{2} / 2 = 0, \\ w_{1}, w_{2} \geq 0 ‚ \end{array}$ $\begin{array}{l} \max d = \max (\frac{91 800}{w_{1}})^{w_{1}} (\frac{0.01}{w_{2}})^{w_{2}}, \\ s . t . w_{1} + w_{2} = 1, - w_{1} + w_{2} / 2 = 0, \\ w_{1}, w_{2} \geq 0 ‚ \end{array}$

最优解为w₁ = 1/3, w₂ = 2/3;目标最优值为d₀=3.9571。从而得到确定性几何规划式 (14) 的近似最优解为S₀≈69 595 kVA。

2) 解确定性几何规划

$\begin{array}{l} \min {91 800 S^{- 1} + 0.01 S^{1 / 2}}, \\ s . t . 0 < S \leq S_{0} + t_{1} = 71 320 。 (15) \end{array}$ $\begin{array}{l} \min {91 800 S^{- 1} + 0.01 S^{1 / 2}}, \\ s . t . 0 < S \leq S_{0} + t_{1} = 71 320 。 (15) \end{array}$

其中t₁=1 725是根据试验, 且由公式^[8]

《图6》

确定, 这里k=1/λ, λ为在区间[0, 1]中适当选取的数。

求解规划式 (15) 得, d₁=3.960 9。

3) 解确定性几何规划

$\begin{array}{l} \max α, \\ s . t . S + 1 725 α \leq 71 320, \\ - 91 800 S^{- 1} - 0.01 S^{1 / 2} - Ζ_{0} α \leq - d_{1}, \\ S > 0 ‚ \end{array}$ $\begin{array}{l} \max α, \\ s . t . S + 1 725 α \leq 71 320, \\ - 91 800 S^{- 1} - 0.01 S^{1 / 2} - Ζ_{0} α \leq - d_{1}, \\ S > 0 ‚ \end{array}$

其中Z₀=d₁-d₀=0.003 8。将其化为

$\begin{array}{l} \max α = \min (1 - α) \\ s . t . \frac{- 91 800 S^{- 1} - 0.01 S^{1 / 2}}{- 3.960 9 + 0.003 8 α} \leq 1 ‚ \\ S / (71 320 - 1 725 α) \leq 1, \\ S > 0 。 \end{array}$ $\begin{array}{l} \max α = \min (1 - α) \\ s . t . \frac{- 91 800 S^{- 1} - 0.01 S^{1 / 2}}{- 3.960 9 + 0.003 8 α} \leq 1 ‚ \\ S / (71 320 - 1 725 α) \leq 1, \\ S > 0 。 \end{array}$

它的项数J=4, 变量个数m=2, 困难度D=4-2-1 , 对偶规划为

$\begin{array}{l} \max (\frac{1 - α}{w_{00}})^{w_{00}} (\frac{- 91 800 / w_{01}}{- 3.960 9 + 0.003 8 α})^{w_{01}} \cdot \\ (\frac{- 0.001 / w_{02}}{- 3.960 9 + 0.003 8 α})^{w_{02}} (\frac{1 / w_{11}}{71 320 - 1 725 α})^{w_{11}} \cdot \\ (w_{01} + w_{02})^{w_{01} + w_{02}} w_{11}^{w_{11}} ； (16) \\ s . t . w_{00} = 1, w_{01} + w_{02} = 1, \\ - w_{01} + w_{02} / 2 + w_{11} = 0, \\ w_{00}, w_{01}, w_{02}, w_{11} \geq 0 。 (17) \end{array}$ $\begin{array}{l} \max (\frac{1 - α}{w_{00}})^{w_{00}} (\frac{- 91 800 / w_{01}}{- 3.960 9 + 0.003 8 α})^{w_{01}} \cdot \\ (\frac{- 0.001 / w_{02}}{- 3.960 9 + 0.003 8 α})^{w_{02}} (\frac{1 / w_{11}}{71 320 - 1 725 α})^{w_{11}} \cdot \\ (w_{01} + w_{02})^{w_{01} + w_{02}} w_{11}^{w_{11}} ； (16) \\ s . t . w_{00} = 1, w_{01} + w_{02} = 1, \\ - w_{01} + w_{02} / 2 + w_{11} = 0, \\ w_{00}, w_{01}, w_{02}, w_{11} \geq 0 。 (17) \end{array}$

式 (17) 的一般解为

$\begin{array}{l} {\begin{cases} w_{01} = 1 - w_{02} \\ w_{11} = 1 - \frac{3}{2} w_{02} \end{cases} \Rightarrow \\ {\begin{cases} w = (w_{00}, 1 - w_{02}, w_{02}, 1 - \frac{3}{2} w_{02})^{Τ}, \\ 0 \leq w_{02} \leq \frac{2}{3} \end{cases} \end{array}$ $\begin{array}{l} {\begin{cases} w_{01} = 1 - w_{02} \\ w_{11} = 1 - \frac{3}{2} w_{02} \end{cases} \Rightarrow \\ {\begin{cases} w = (w_{00}, 1 - w_{02}, w_{02}, 1 - \frac{3}{2} w_{02})^{Τ}, \\ 0 \leq w_{02} \leq \frac{2}{3} \end{cases} \end{array}$

这是一维线性约束优化问题。如取w₀₂=2/3, 得

$w = (w_{00}, w_{01}, w_{02}, w_{11})^{Τ} = (1, \frac{1}{3}, \frac{2}{3}, 0)^{Τ} ‚$ $w = (w_{00}, w_{01}, w_{02}, w_{11})^{Τ} = (1, \frac{1}{3}, \frac{2}{3}, 0)^{Τ} ‚$

对偶规划的目标函数为

$\bar{d} = (1 - α) \frac{(- 275 400)^{1 / 3} (- 0.015 015)^{2 / 3}}{- 3.960 9 + 0.003 8 α} 。$ $\bar{d} = (1 - α) \frac{(- 275 400)^{1 / 3} (- 0.015 015)^{2 / 3}}{- 3.960 9 + 0.003 8 α} 。$

利用式子

$1 - α = \bar{d} \Rightarrow - 3.960 9 + 0.003 8 α = - 3.959 67 ‚$ $1 - α = \bar{d} \Rightarrow - 3.960 9 + 0.003 8 α = - 3.959 67 ‚$

即得α=0.337, 从而

$d = \frac{- 3.960 9 + 0.003 8 α}{1 - α} \bar{d} = 3.960 9 ‚$ $d = \frac{- 3.960 9 + 0.003 8 α}{1 - α} \bar{d} = 3.960 9 ‚$

获得式 (13) 的最小值为3.960 9。利用公式^[5]

$\begin{array}{l} {\begin{cases} 91 800 S^{- 1} = \frac{1}{3} \times 3.960 9 \\ 0.01 S^{1 / 2} = \frac{2}{3} \times 3.960 9 \end{cases} (18) \\ \Rightarrow {\begin{cases} S_{1} \approx 69 530 \\ S_{2} \approx 69 728 ‚ \end{cases} \\ S = (S_{1} + S_{2}) / 2 \approx 69 629 ‚ \end{array}$ $\begin{array}{l} {\begin{cases} 91 800 S^{- 1} = \frac{1}{3} \times 3.960 9 \\ 0.01 S^{1 / 2} = \frac{2}{3} \times 3.960 9 \end{cases} (18) \\ \Rightarrow {\begin{cases} S_{1} \approx 69 530 \\ S_{2} \approx 69 728 ‚ \end{cases} \\ S = (S_{1} + S_{2}) / 2 \approx 69 629 ‚ \end{array}$

即得到模型Ⅰ的近似最优解为S= 69 629, 近似Fuzzy最优值为3.960 9。由式 (9) ～ (11) , 得:

$R \approx 1.31 ‚ Ν_{b} = \frac{49.03}{π R^{2}} \approx 9.1 。$ $R \approx 1.31 ‚ Ν_{b} = \frac{49.03}{π R^{2}} \approx 9.1 。$

当σ取5 915, 110 kV变电所经济容量S=69 629∈[69 530, 69 728] 时, 经济供电半径R≈1.31 km。该市需建设110 kV变电所计算值9.1个。

《3.2模型Ⅱ》

3.2模型Ⅱ

假定模型中函数的系数为在区间内变化的Fuzzy数。设式 (12) 的目标函数的第二个系数 $\tilde{c}$ $\tilde{c}$ ₂∈[0.008, 0.03] , 其隶属函数为^[5]:

$φ (c_{2}) = {\begin{cases} 0 c_{2} \leq 0.008 \\ \frac{(c_{2} - 0.008)^{2}}{0.000 484} 0.008 < c_{2} < 0.03 。 \\ 1 c_{2} \geq 0.003 \end{cases} (19)$ $φ (c_{2}) = {\begin{cases} 0 c_{2} \leq 0.008 \\ \frac{(c_{2} - 0.008)^{2}}{0.000 484} 0.008 < c_{2} < 0.03 。 \\ 1 c_{2} \geq 0.003 \end{cases} (19)$

由式 (19) 有φ (c₂) ≥α, 则得 $c_{2} = 0.008 + 0.22 \sqrt{1 - α}$ $c_{2} = 0.008 + 0.22 \sqrt{1 - α}$ , 规划式 (12) 变为

$\begin{array}{l} \min {91 800 S^{- 1} + (0.008 + 0.22 \sqrt{1 - α}) S^{1 / 2}}, \\ s . t . S > 0 。 (20) \end{array}$ $\begin{array}{l} \min {91 800 S^{- 1} + (0.008 + 0.22 \sqrt{1 - α}) S^{1 / 2}}, \\ s . t . S > 0 。 (20) \end{array}$

此为含Fuzzy系数的正项几何规划, 即为模型Ⅱ, 它的对偶形式为

$\begin{array}{l} \max (\frac{91 800}{w_{0}})^{w_{0}} (\frac{0.008 + 0.022 \sqrt{1 - α}}{w_{1}})^{w_{1}} ‚ \\ s . t . w_{0} + w_{1} = 1, - w_{0} + w_{1} / 2 = 0, \\ w_{0}, w_{1} \geq 0 ‚ α \in [0 ‚ 1] 。 \end{array}$ $\begin{array}{l} \max (\frac{91 800}{w_{0}})^{w_{0}} (\frac{0.008 + 0.022 \sqrt{1 - α}}{w_{1}})^{w_{1}} ‚ \\ s . t . w_{0} + w_{1} = 1, - w_{0} + w_{1} / 2 = 0, \\ w_{0}, w_{1} \geq 0 ‚ α \in [0 ‚ 1] 。 \end{array}$

解得w₀ =1/3, w₁ = 2/3。当取α=0.8时, 有d≈3.688 7。利用模型Ⅰ的求解步骤3中的式 (18) , 获得式 (20) 的最优解为S=74 660.45 。S和d亦即为模型Ⅱ的近似最优解和最优值。且当取α=0.8时, 由式 (9) ～ (11) , 得R=1.35, N_b≈8.56。

《4 结果比较分析》

4 结果比较分析

将静态模型、动态模型^[1]、本文模型Ⅰ, Ⅱ的计算结果列于表1。

表1 S, R和N_b的比较表

Table 1 Comparison of S, R and N_b

《表1》

σ=5 915 kW·km^-2	S/kVA	R/km	N_b
静态	66 100	1.27	9.68
动态	71 320	1.32	8.96
几何规划	69 595	1.27	9.2
模型Ⅰ	69 629	1.31	9.09
模型Ⅱ	74 660.45	1.35	8.56

对于不同的σ_j可计算出110 kV变电所的经济容量S_j, 经济供电半径R_j和变电所的个数N_b 。

实际上, 该市在2001年前将规划建设6～10个110 kV变电所, 上述结果与实际比较符合, 可应用于城市电网规划。但从表1中看到, 动态模型优于静态模型, Fuzzy几何规划模型Ⅰ和Ⅱ明显优于静态模型和几何规划模型, 甚至比动态模型更优。同时, 对于高负荷水平, 表1中变电所选的容量偏小, 变电所的个数偏多, 这主要是没有考虑负荷的变化增长过程及变电所建设的投资过程 (土地征用费及配电线的建设费等的增长) , 使得经典模型及其方法在城市电网建设中执行起来比较困难。但用模型Ⅰ和Ⅱ考虑目标的伸缩、系数的波动 (当然, 约束条件的伸缩与其系数的波动亦可作类似的讨论, 在此略去) 。这样模型可包含更多的信息, 给人们的决策留有充分的余地。决策者可根据实际需求进行调整。例如, 可选择经济容量偏大, 变电所个数偏少的最优方案, 以期达到最佳的效果。

如果再考虑变电所和中压配电线路的投资费用系数, 以及电价随时间变化等因素的影响, 其效果将会更好些。

《5 结束语》

5 结束语

本文建立的模型, 对于确定的阈值α和城区的不同平均负荷密度σ_j , 在变电所允许的经济容量S_j下, 可以很快求出平均供电半径R_j 。当Fuzzy几何规划的困难度D>0时, 可用搜索法求相应的形如式 (16) 、式 (17) 的参数几何规划最优解。这样, 利用Fuzzy几何规划, 建立一个系统控制模型, 根据实际需求调整其参数α, σ_j 和S_j (j=1, …, r) , 使之在变电所的最大经济容量之下, 求得最经济的供电半径, 而使年费用最小。

Show More