固体微结构表面稳定性在冶金、微电子、化工和生物医药等方面具有十分重要的意义。现有的研究发现，在表面张力和其他因素的联合作用下，微结构的表面会发生失稳[1 ~ 3] 。软物质的弹性模量、剪切模量远小于金属等固体，因此，在表面张力作用下易发生变形，表面效应更为明显，易发生失稳现象。正如 Tanaka 等实验所发现的[4] ，丙烯酰胺微柱形胶体在一定条件下会产生泡状和竹节状等失稳现象。假设在发生失稳的初始阶段，是线性小变形范围且无质量迁移和物质扩散行为的弹性失稳。笔者的目的就是研究柱形胶体发生弹性失稳的条件及其影响因素。

对于弹性固体微结构的稳定性，前人做了许多研究工作。例如，一个半无限大的固体在表面张力的作用下表面的形貌会发生变化[5 ~ 9] ；须状微结构在受拉时会发生轴向失稳[10 ~ 12] ；发生轴向失稳的同时也会发生径向失稳[13 ,14] 。对这些失稳的研究采用的方法是：考虑质量的迁移或物质扩散行为，从能量角度出发，通过比较失稳前后的能量差，导出发生失稳的条件，并考虑表面能对结构稳定性的影响，但是没有进一步考虑表面张力引起的应变能的改变，也没有讨论微结构的尺寸、材料属性与稳定性的相关性。对于 Tanaka 等的试验发现的柱形胶体失稳，可以认为表面效应是影响形变的主要因素。 B. Barriere 等针对柱形胶体的弹性失稳问题进行了详细研究[15] ，但在求解过程中采用了位移边界条件，等于施加了一个径向位移约束，实质上是表面张力与外场的联合作用下的柱形体失稳问题，没有反映出表面张力单独作用下柱形体是否会发生弹性失稳。 K. G. Kornev 等研究了半无限大自由表面的薄膜仅在表面张力作用下会发生弹性失稳，失稳与薄膜厚度及材料属性相关[5 ,16] ，表现了微结构失稳的尺寸相关性，揭示了仅有表面作用也会导致薄膜发生弹性失稳。对于柱形胶体来说，在表面作用下是否也会产生尺寸与材料属性相关的弹性失稳？笔者针对该问题做了研究，采用能量泛函变分的方法，得到失稳判据方程，其与柱形体的半径、失稳的波长及材料的属性相关。

《1   柱形胶体弹性失稳分析 》

1   柱形胶体弹性失稳分析 　 　

表面弹性失稳的模型如图 1 所示，该模型是半径为 R 的各向同性长圆柱形胶体，仅在表面张力 作用下，表面会发生弹性失稳。实线表示表面张力作用下失稳前的形貌，点划线表示柱形体的可能的失稳形貌。

《图 1》

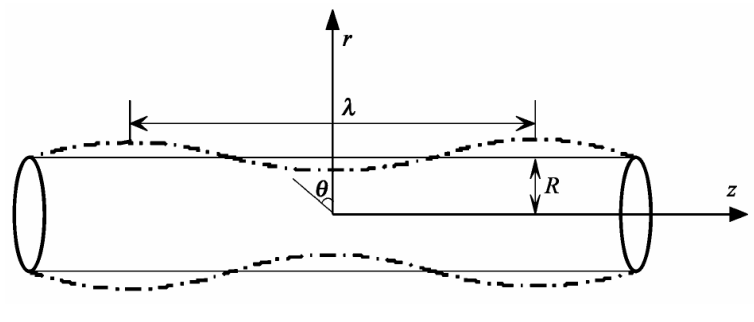
图 1 各向同性柱形体在表面张力作用下的失稳

Fig.1 The instability patterns of isotropic gel cylinder on the surface stress

令扰动波长为 ，波数为 k = 2π/ ，圆柱体长为 L0 且 L0 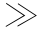 。柱形体的各点用柱坐标系（r，θ，z）描述，r 为径向坐标，柱形体的表面 r ＝ R ，取 θ 方向位移 uθ＝ 0 ，即可简化为轴对称问题。

系统的能量泛函可以写成：

式中  为弹性能 , 为表面能。

变形后的形态如图 2 所示， ur 为 r 方向位移；uz 为 z 方向位移；z 方向的位移增量为 dz ＋ duz ；r 方向的位移增量为 dur，这与初始状态 r ＝ R 时的情况相比，表面积为 dS ＝（R ＋ ur）［（dz ＋ duz）2 + （dur）2 ] 1/2 ，令初始状态柱面积微元 d S0＝ Rdθdz ，则发生失稳后为

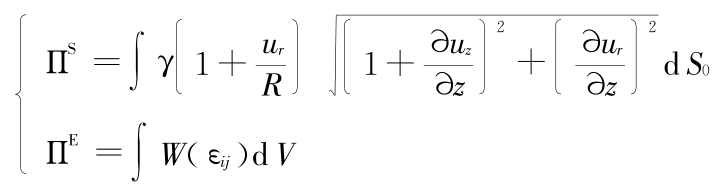
式中 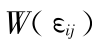是应变能密度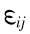， 是应变张量，dV 是柱形体体积微元。

《图 2》

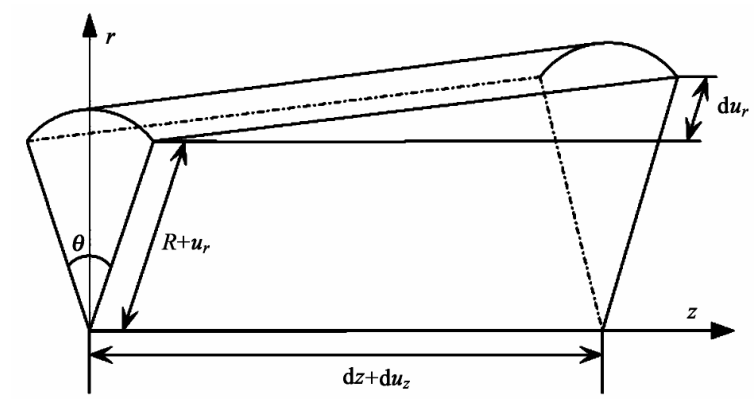
图 2 柱形体失稳后的微元体示意图

Fig.2 The sketch of gel cylinder instability

将式（2）代入式（1），对位移取变分，并分步积分，略去高阶小量，由于柱形体的两个端面平衡，可得到能量泛函变分为

式中 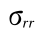为径向应力，为切向应力，并且由于位移 的任意性，且考虑系统无体力，由此可得平衡方程为

同时也可以得到边界条件为

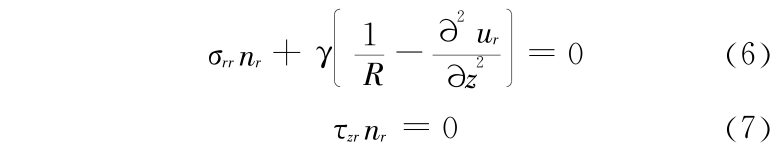
初始状态 r = R 时为柱面，仅受表面张力的作用，径向位移 ur 仅与径向坐标 r 相关，则  ，轴向位移 uz 仅与轴向坐标 z 有关，θ 向位移 uθ = 0 ，同样也是一个轴对称问题，由失稳后的边界条件式（6）和式（7）退化，可以得到初始状态的的边界条件为

式中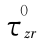 和 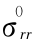 为无初始状态的应力，外法线方向矢量 n ＝（1，0，0）

对于无失稳的初始状态求解，可将位移解设为

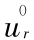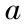式中 和 分别是初始状态 r 方向和 z 方向位移， 为待定系数，运用虎克定律将式（10）和式（11）代入式（4）和式（5），并利用边界条件式（8）和式（9）可以解得

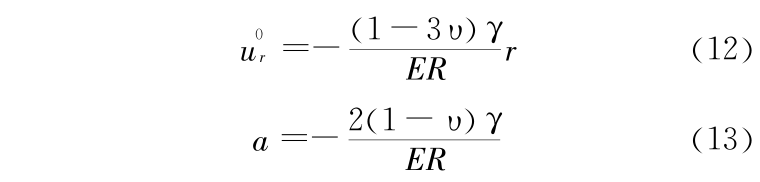
式中 E 为弹性模量，υ 为波松比，由此 z 向位移可以表示为

对于柱形体失稳后的轴对称问题，其应力张量 σ 和位移矢量 u 仅是 r 和 z 的函数，可用柱坐标下的应力函数方法得知，应力和位移完全由双调和函数 Ф（r，z）决定。双调和函数 Ф（r，z）满足

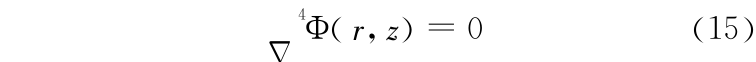
对于柱面上应力作用的解答，可以设应力函数为

式中 e 为失稳后的小扰动振幅，I0（kr）和 I1（kr）分别是零阶和一阶的修正 Bessel 函数， A 和 B 是两个待定的常数。由此失稳后体内的应力和位移可以很容易由式（16）导出，例如，满足平衡条件的径向应力可以写为

式中

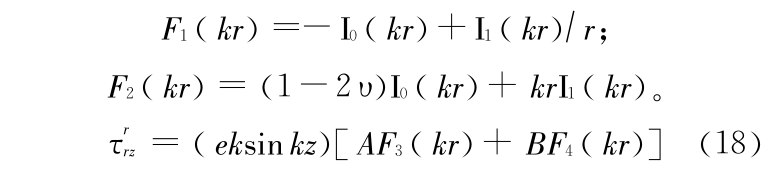
式中

失稳后的边界条件式（6）和式（7）包含了初始状态的边界条件式（8）和式（9），因此失稳后的应力边界条件为

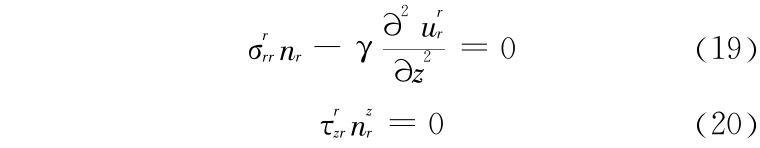
将式（17）和式（18）代入式（19）和式（20）可得

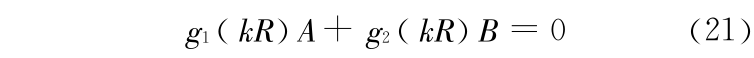
式中

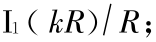
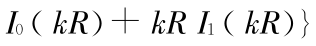，是反映材料属性的内禀尺度。

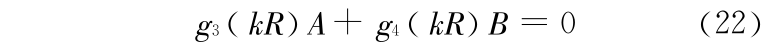
式中  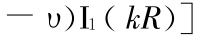；，显然联立方程（21）和（22）是一个齐次方程组，而得不到 A 和 B 的非零解，只能得到 A 和 B 有非零解的判据，该判据就是方程组的系数行列式为零：

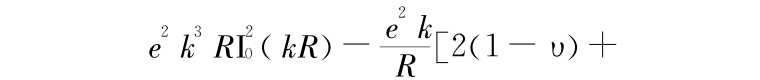
《2   讨论》

2   讨论 　 　

可以看出判据方程式（23）是关于半径、内禀尺度和波长的方程，这 3 个变量都是长度量纲，对其无量纲化，有两种方式，一种是取内禀尺度为基本量，将半径和波长化为无量纲的半径和波长。另一种取半径为基本量，将内禀尺度和波长无量纲化。先讨论第一种情况：

取内禀尺度 L0 为基本量，可以将判据方程无量纲化：

显然，这是一个关于无量纲化的失稳半径 R * = R/L0 和波长 = 2π/ kL0，以半径 R *为横坐标，波长 为纵坐标，如图 3 所示。

《图 3》

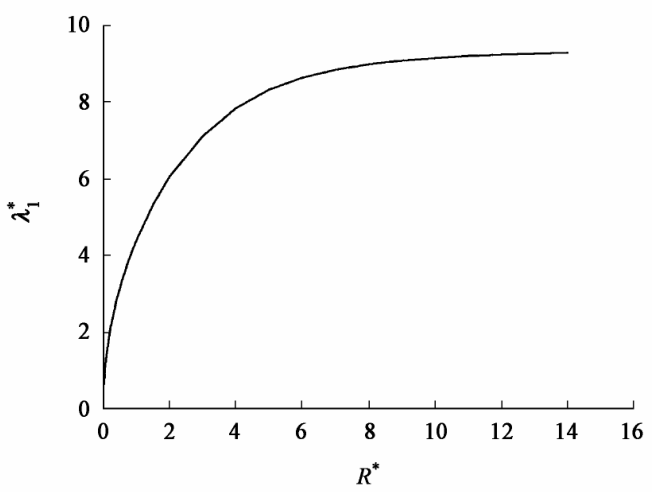
图 3 内禀尺度为基本量，柱体发生失稳的波长与半径间的关系

Fig.3 The relation between the wavelength and the radius with the intrinsic scale being basic variable

图３曲线对应材料会发生失稳的点。在内禀尺度为基本量情况下，随着半径的增大，波长也逐渐增大。在半径很小时，微小的半径变化会引起波长的急剧变化，此时半径对表面效应贡献明显。随着半径的增大，波长增速逐渐变缓，最后趋近于某一个固定值。当波长小于该固定值时，应力松弛造成弹性能的减小大于表面能的增加，从而发生失稳；当波长大于该固定值时，表面能的增加大于应力松弛造成的弹性能的减小，因而不会发生失稳。 A . Boudaoud 等讨论了 Tanaka 等的试验中柱形胶体失稳在出现泡状时，失稳的波长与半径是成比例的，在出现竹节状时失稳的波长与半径的平方根成正比 [17] 。由此可见笔者的结果与其趋势是一样的。

另一种无量纲化的方法是取初始半径 R 为基本量，可得无量纲的判据方程为

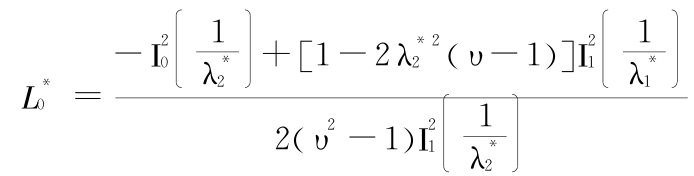
显然，这是一个关于无量纲内禀尺度 = L0 /R 和无量纲波长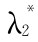 = 2π/ kR 的隐式方程，以内禀尺度 为横坐标，以波长λ倡 2 为纵坐标，如图 4 所示。

《图 4》

图 4 以半径为基本量，无量纲失稳波长与内禀尺度之间关系

Fig.4 The relation between intrinsic scale and wavelength with radius being basic variable

由图 4 可以看出，当内禀尺度很小，对应材料很硬或者表面张力很小时，波长也很小，这反映了表面效应不容易观察到；当内禀尺度为零时，无表面作用，显然不会失稳；随着内禀尺度的增大，对应材料很软或者表面张力很大时，波长也增大；失稳的波长较大，失稳现象容易观察到，反映了表面效应比较明显。

由图 3 和图 4 及以上的讨论可以看出，柱形体发生失稳是材料的内禀、半径和失稳波长三者相互影响的结果。

《3   结论 》

3   结论 　 　

笔者采用一个简单的弹性模型，对包括表面能和表面应力造成的弹性能的能量泛函进行位移变分，求出了非经典的边界条件，得到了失稳判据方程，发现对于固定的材料来说，随着半径的增大，发生失稳的波长也增大；对于金属类硬物质，很难发生失稳；而对于胶体类软物质，则较容易发生失稳。这是由于软物质的内禀尺度大，即刚度小，更容易发生形变的缘故。

致谢：感谢中国科学技术大学力学和机械工程系何陵辉教授的指导；感谢加拿大温哥华英属哥伦比亚大学机械工程系田利安与作者进行讨论。