《1 前言》
1 前言
高斯数值积分是一种有效的高精度数值计算方法。在工程数值计算、固体物理学、光电子学等领域常用来对难以获得解析解的积分进行数值计算。例如,在工程电磁场计算中常用的贝塞尔函数[1] ,如果采用其级数解来计算,需考虑很复杂的递推稳定性问题;反之,若从它的积分形式出发来计算,采用数个节点的高斯积分,即可获得满意的数值精度。在 X 射线衍射中的线形分析和光谱学中,Voigt 函数能较好地描述 X 射线衍射峰和光谱峰的线形,但该函数没有解析的积分解;固体物理学中热容表达式中的德拜函数也无解析的积分解。用高斯数值积分则可方便地计算这些积分。
n 个节点数值积分可表示为

式中 ρ(x)是在积分区间( ,b)上的正权重函数,
,b)上的正权重函数,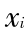 和
和  是与函数
是与函数  无关的节点和权重因子。合理地选择不同的节点 x1 , x2 ,…, xn ,使数值积分公式(1)对次数
无关的节点和权重因子。合理地选择不同的节点 x1 , x2 ,…, xn ,使数值积分公式(1)对次数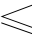 2n - 1 的多项式精确成立,即为高斯积分公式,它的代数精度为 2n - 1 。在所有的 n 个节点积分公式中,高斯积分有最高的代数精度。
2n - 1 的多项式精确成立,即为高斯积分公式,它的代数精度为 2n - 1 。在所有的 n 个节点积分公式中,高斯积分有最高的代数精度。
可以证明,积分公式(1)为高斯积分的充要条件是积分节点为正交多项式的根[2] 。不同的高斯积分公式如高斯-勒让德、高斯-拉盖尔、高斯-厄米、高斯-切比雪夫积分的积分区间和正权重函数不同 [3] 。高斯-勒让德、高斯-拉盖尔、高斯-厄米、高斯-切比雪夫的正权重函数和积分区间分别为 1 和[ -1 ,1 ] ,e-x 和[0 ,∞), 和(-∞,+∞),(1 - x2)-1/2 和[ -1 ,1]。
和(-∞,+∞),(1 - x2)-1/2 和[ -1 ,1]。
很多文献可以查到高斯积分公式的节点 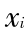 和权重因子
和权重因子  值 [4 ~ 6] 。对于非振荡的被积函数,只需要用数个节点来计算,便可获得良好的积分精度,更高的精度可用更高次的公式来获得。现能查到的高斯-勒让德、高斯-拉盖尔、高斯-厄米积分的最高次节点和权重因子分别为 96 ,15 和 20[4] 。
值 [4 ~ 6] 。对于非振荡的被积函数,只需要用数个节点来计算,便可获得良好的积分精度,更高的精度可用更高次的公式来获得。现能查到的高斯-勒让德、高斯-拉盖尔、高斯-厄米积分的最高次节点和权重因子分别为 96 ,15 和 20[4] 。
为了获得更精确的积分值,需要有更高次的积分节点和权重因子。由于计算机的精度有限,其舍入误差往往会在多项式的次数很高或自变量很大的情况下,给多项式值的计算带来很大误差,导致高阶积分节点及权重因子的计算很困难[7] 。计算正交多项式的节点可以用牛顿法或魏尔斯特拉斯法[8] ,但计算表明,对于高阶正交多项式,要获得全部的根很困难。 G. V. Milovanovic'等给出了一个计算正交多项式根的算法[9] ,但需给出足够精确的初始值。对于 n →∞ 的勒让德正交多项式 Pn(x),也可用渐进展开以获得其零点,Pn(x)的第 k 个零点渐进展开通常有两类,第一类展开需用到贝塞尔函数 J0(x)的第 k 个根,第二类则包含了三角函数[10] 。数值实验表明,对于给定的 n ,这些近似展开的精度在很大程度上依赖于 k 的取值范围(1 k
k  [ n/2 ])。 F. G. Lether 等发展了勒让德多项式 Pn(x)的第 n 个正零点的极小化最大三角近似[10] ,可获得 n
[ n/2 ])。 F. G. Lether 等发展了勒让德多项式 Pn(x)的第 n 个正零点的极小化最大三角近似[10] ,可获得 n 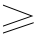 2 时 4.2 个有效位数,用于估计勒让德多项式根的初始值,以便迭代求解。 P. N. Swarztrauber 比较了计算高斯-勒让德积分的节点和权重因子的三种方法:本征值方法,Yakimiw 方法和 Fourier-Newton 法 [11] 。本征值方法的节点和权重误差随 n 的增长分别为 O(n)和 O(n2);Yakimiw 方法的节点和权重误差则为 O(1),逐点相关误差是一致的,即使在积分端点处节点趋近于 0 时,所有权重 r 仍具有相同的有效位数,但在 x =± 1 处,由于机器精度的原因,高斯-勒让德节点的二次群聚使得根产生合并甚至交换; Fourier-Newton法基于直接计算变换点θi = arccos xi ,不发生群聚。 E. Babolian 等把积分限
2 时 4.2 个有效位数,用于估计勒让德多项式根的初始值,以便迭代求解。 P. N. Swarztrauber 比较了计算高斯-勒让德积分的节点和权重因子的三种方法:本征值方法,Yakimiw 方法和 Fourier-Newton 法 [11] 。本征值方法的节点和权重误差随 n 的增长分别为 O(n)和 O(n2);Yakimiw 方法的节点和权重误差则为 O(1),逐点相关误差是一致的,即使在积分端点处节点趋近于 0 时,所有权重 r 仍具有相同的有效位数,但在 x =± 1 处,由于机器精度的原因,高斯-勒让德节点的二次群聚使得根产生合并甚至交换; Fourier-Newton法基于直接计算变换点θi = arccos xi ,不发生群聚。 E. Babolian 等把积分限  ,b 看作两个变量,以获得较精确的单项式
,b 看作两个变量,以获得较精确的单项式  = x j 的高斯积分公式[12] 。然而,此方法的应用范围很有限。
= x j 的高斯积分公式[12] 。然而,此方法的应用范围很有限。
为了获得高次勒让德多项式、拉盖尔多项式和厄米多项式的根,以用于高斯积分,笔者也尝试了数值方法中的多种非线性求根方法,如二分法、割线法、抛物线法(穆勒法)、x = g(x)的简单迭代法、牛顿法、牛顿下山法、林士谔-赵访熊法(劈因子法),这些方法在求解高次正交多项式时,都存在如下问题:无法找到全部根,迭代精度进行到一定程度便无法进行迭代,不能获得所需的迭代精度,或者迭代过程无法收敛。
笔者提出了高精度高次勒让德、拉盖尔和厄米多项式的一种求根方法:先在不影响它们的根的情况下,对其定义稍作变化,然后在一定范围内尝试以不同步长来搜索其全部根所在的区间范围,再以常用的根迭代办法来求根。实验表明这种方法———笔者称作搜索迭代法(SIM ,scan-iteration method)是非常有效的,能正确获得高次正交多项式的全部根,计算速度很快,精度高。
《2 高次多项式的计算》
2 高次多项式的计算
《2.1 勒让德多项式》
2.1 勒让德多项式
勒让德多项式定义为

式中 - 1  x
x  1 。
1 。
勒让德多项式有递推关系:
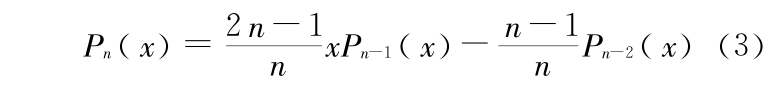
假设仅在第 1 和第 2 个计算步骤中存在舍入误差,由于该误差传播的影响,Pn(x),Pn - 1(x),Pn -2(x)分别变为  ,满足公式(3)。让
,满足公式(3)。让  ,则可得到方程
,则可得到方程

式中 bn =(2n - 1)/n , cn =-(n - 1)/n 。称式(4)为式(3)的误差方程。
当 n 很大时,bn → 2 , cn → 1 ,式(4)近似为
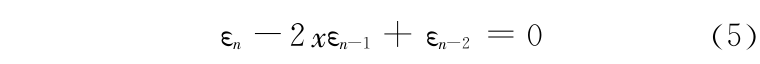
式(5)为线性齐次差分方程,其特征方程为

式(6)的根为 r1 = x + i (1 - x 2)1/2 ,r2 = x - i (1 - x 2)1/2 。
此处 i 为虚数单位。|r1|=1,|r2|= 1 。根据递推稳定性定理[1] ,可知递推关系式(3)是稳定的。由 P0 = 1 ,P1 = x 和式(3),勒让德多项式的值能在可控的误差下做向前递推计算。
高斯-勒让德积分的权重因子为

式中 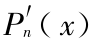 是勒让德多项式 Pn 的导数,其计算式为
是勒让德多项式 Pn 的导数,其计算式为
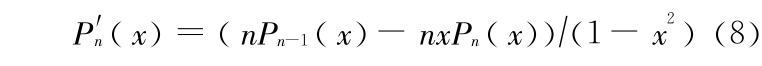
《2.2 拉盖尔多项式》
2.2 拉盖尔多项式
在大多数文献中,拉盖尔多项式定义为
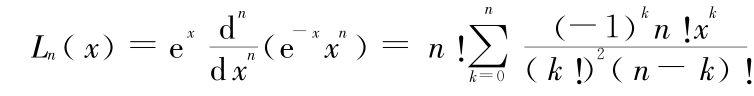

式中 x ∈[0 ,∞)。可以看到 Ln(x)∝(n !)2 ,它的值随着 n 值的增加迅速增大,致使计算机发生计算溢出错误。现在看一个具体算例,拉盖尔多项式的系数  可由如下递推关系计算:
可由如下递推关系计算:

计算得  (k = 0 ,…, n),
(k = 0 ,…, n), ,把所有的
,把所有的  ×
×  的值相加,记为算法 1 ;再用较精确的算法(记为算法 2)来计算拉盖尔多项式[6] :
的值相加,记为算法 1 ;再用较精确的算法(记为算法 2)来计算拉盖尔多项式[6] :

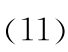
表 1 列出了幂次为5 ,100的拉盖尔多项式用双精度(其大小为 10 字节,数值范围为 3.6 × 10-4 951 ~ 1.1 × 104 932 ,有效小数点为 9 ~ 20 位)的计算结果。
从表 1 可以看到,对于 L5(x),算法 1 和算法 2 给出了一致的计算结果。而对于 L100(x),在小变量 x = 0.1 时尚给出相同数量级的计算结果,而当 x = 1,10,100 时,两种计算结果的差别是巨大的,连符号都相反,因此计算结果不可信。
《表 1》
表 1 两种算法计算 L100(x)和 dL5(x)的结果比较
Table 1 Comparison of computational results between L100(x) and L5(x) obtained by two algorithms

式(9)定义的拉盖尔多项式的递推关系为
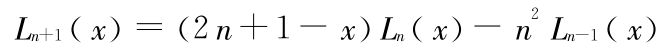

此递推关系是不稳定的。如果采用式(12)来计算拉盖尔多项式 Ln(x),舍入误差将会随着递推的进行而不断被放大,致使难以获得多项式的精确值。
笔者要获得的是拉盖尔多项式的根,为此可对拉盖尔多项式稍做修改,将拉盖尔多项式定义为
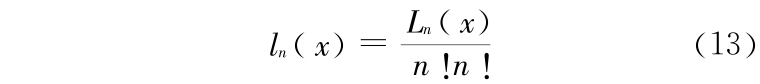
方程(13)与方程(9)有相同的根,但它的值不再正比于(n !)2 。相应地,式(13)的递推关系为

式(14)的误差方程为
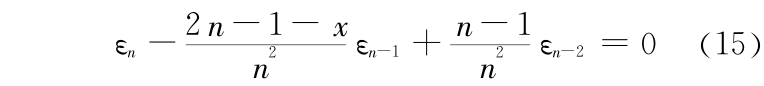
当 n 是很大的自变量时,对于一定的 x 值,式(15)变为

这表明向前递推关系式(14)是稳定的。由

则能在可控制的误差下由递推关系式(14)来计算拉盖尔多项式 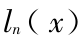 。
。
高斯-拉盖尔的积分重因子计算式为

《2.3 厄米多项式》
2.3 厄米多项式
厄米多项式定义为

式中 x ∈(-∞,+∞);

其关系为 Hn(x)=(-1)n H(x)。
如果 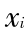 是 Hn(x)的根,-
是 Hn(x)的根,-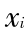 也是它的根。当求方程(19)的根时,可以先在区间[0 ,+∞)上求解 [ n/2 ]个根,然后借此关系获得它所有的根。
也是它的根。当求方程(19)的根时,可以先在区间[0 ,+∞)上求解 [ n/2 ]个根,然后借此关系获得它所有的根。
厄米多项式(19)的递推关系为

从式(19)可以看出,厄米多项式的值正比于 n !,这使得在计算它的值时容易发生计算溢出。为了避免计算溢出,把厄米多项式的定义稍做变换,记为 hn ,
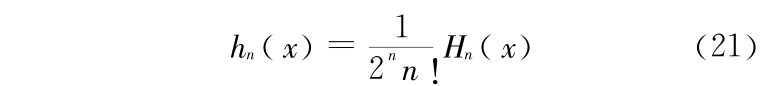
由式(20)、式(21)可得 hn 的递推关系为


Hn 和 hn 具有相同的根。方程(22)的误差方程为

当 n 值很大时,方程(23)变为

这表明式(22)向前递推计算是稳定的。根据式(22),得

可在可控误差下计算  的值。
的值。
高斯-厄米积分权重因子的计算式为
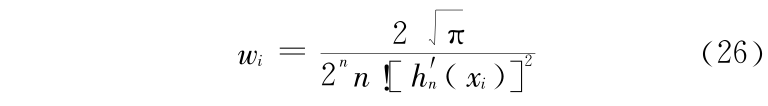
《3 由搜索迭代法求高次多项式的根》
3 由搜索迭代法求高次多项式的根
现在来讨论上述多项式的一种求根方法。用此种方法可以很容易获得高精度的高次勒让德、拉盖尔和厄米多项式的根。
上述 n 次正交多项式在其定义区间有 n 个互异的根。 n 次勒让德多项式和厄米多项式分别在(0 ,1)和(0 ,+∞)区间有[ n/2 ]个根 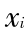 ,剩余的根则为-
,剩余的根则为-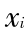 (i = 0 ,1 ,2 ,…,[ n/2 ])和 0(当 n 是奇数时); n 阶拉盖尔多项式则在(0 ,+∞)区间有 n 个根。对于任一有限值 n ,这些多项式的根都在一有限的范围内。例如当 n =10,100,1000时,拉盖尔多项式的根全部分别位于(0.1 ,30)、(0.01 ,374.99)和(0.001 ,3 943.248)区间,厄米多项式的根则全部分别位于(0.3 ,3.5)、(0.1 ,13.5)和(0.03 ,44.21)区间。
(i = 0 ,1 ,2 ,…,[ n/2 ])和 0(当 n 是奇数时); n 阶拉盖尔多项式则在(0 ,+∞)区间有 n 个根。对于任一有限值 n ,这些多项式的根都在一有限的范围内。例如当 n =10,100,1000时,拉盖尔多项式的根全部分别位于(0.1 ,30)、(0.01 ,374.99)和(0.001 ,3 943.248)区间,厄米多项式的根则全部分别位于(0.3 ,3.5)、(0.1 ,13.5)和(0.03 ,44.21)区间。
另外,对于任何根 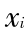 而言,多项式的值在根两侧 x ,y( x <
而言,多项式的值在根两侧 x ,y( x <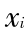 < y)处的正负号相反。
< y)处的正负号相反。
根据多项式的这些特点,对 n 次数多项式,可以在一定的区间范围(0 ,R)确定出[ n/2 ]个根所在的区间范围(rx,i , ry,i )(i = 0 ,1 ,2 ,…,[ n/2 ],对于拉盖尔多项式,[ n/2 ]应为 n)。由于高次多项式的根很多,用多项式曲线来确定各个根的区间的方法不实用,因此采用了自动搜索方法,如图1所示(图中“RootNo”用于存储根数目,“MaxNo”用于存储程序所允许的最大搜索次数,“ P(xj )”表示变量为“ xj ”的多项式的值,“Sign( P(xj ))”表示 P(xj )的符号。对于勒让德多项式,即 R ≡ 1)。先假设一个相对较小的范围 R 和搜索步进 S 进行搜索。如果[ n/2 ]个根区间(rx,i , ry,i )(i =0,1 ,2 ,…,[ n/2 ])被搜索到,则搜索停止;否则再减小步进 S 重新进行搜索。如此反复,直到[ n/2 ]个根区间全部搜索到或者搜索次数{R/S}大于最大的允许搜索次数({R/S}表示取 R/S 值的整数部分)时停止搜索。
《图 1》

图 1 搜索根区间流程图
Fig.1 Flow diagram of searching root
可以看出,只要设定的(0 ,R)区间范围包含了所有 n 次正交多项式的根,则只需步进 S 的值足够小,根的区间总可以被全部找到。
找到多项式的[ n/2 ]或 n 个根区间后,再用通常的迭代方法如割线法、牛顿法、二分法进行求解所需精度的根。笔者称这种求根方法为搜索迭代求求解法(SIM)。
以下讨论以 SIM 方法求解正高精度正交多项式的根中出现的问题。
割线迭代法的格式为

在多项式求根迭代过程中,当迭代进行到一定程度后,会出现 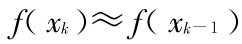 的情况,此时
的情况,此时  -
-  → 0 ,容易导致计算机的计算溢出,迭代过程无法进行。此时,可尝试用牛顿迭代法以避免出现此种情形,即
→ 0 ,容易导致计算机的计算溢出,迭代过程无法进行。此时,可尝试用牛顿迭代法以避免出现此种情形,即

可以看到,式(28)中  的收敛由
的收敛由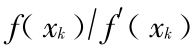 决定,当
决定,当  达到某一精度时,由于有
达到某一精度时,由于有 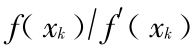 ≈
≈  的近似关系,迭代收敛速度将显著下降。这种情况在求拉盖尔多项式的根时常出现。例如对于求
的近似关系,迭代收敛速度将显著下降。这种情况在求拉盖尔多项式的根时常出现。例如对于求 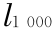 的根时中间的一个迭代系列:
的根时中间的一个迭代系列:

在这种情形下,要获得更高精度的根非常困难。此时,采用二分法(bisection method)可获得令人满意的迭代精度。用牛顿法和二分法来求解拉盖尔多项式的根的一个比较例子见表 2 。可以看出,在此情形下,二分法的收敛速度显著快于牛顿法。
《表 2》
表 2 用牛顿法和二分法求  的根时两种方法的比较
的根时两种方法的比较
Table 2 Comparison of Newton and bisection method to extract roots of 

如果  → 0 ,可采用割线法迭代格式(25)进行迭代求根,以避免由于
→ 0 ,可采用割线法迭代格式(25)进行迭代求根,以避免由于  被
被  除而导致的计算溢出。
除而导致的计算溢出。
数值实验表明,用搜索-割线法迭代求解高斯-勒让德、高斯-厄米积分的节点、用搜索-二分法迭代求解的高斯-拉盖尔的积分节点,可获得满意的迭代精度。
定勒让德多项式、拉盖尔多项式、厄米多项式的根范围(0 ,R)为(0 ,1),(0 , 3 944)和(0 , 50),迭代精度为 10-20 ,求根所花费的时间< 10 min 。这些结果表明,搜索迭代求解算法是一种有效的正交多项式求根方法。
基于以上搜索迭代算法,编写了一个计算程序 PolynominalRoot 对勒让德多项式、拉盖尔多项式、厄米多项式求根。对于 n = 80 和 96 的勒让德多项式、 n = 12 和 15 的拉盖尔多项式、n = 20 的厄米多项式的求根和权重因子的结果与文献[4]给出的结果完全一致。只要给出正确的寻根范围 R ,计算的速度也很快。例如,对于 n < 100 的多项式的求根,在 2 392 MHz CPU 、256 M 内存的 IBM 计算机上求解时,所需时间不超过 1 min ;n = 1 000时,设定勒让德多项式、拉盖尔多项式、厄米多项式的根范围(0 ,R)为(0 ,1),(0 , 3 944)和(0 , 50),迭代精度为 10-20 ,求根所花费的时间< 10 min 。这些结果表明,搜索迭代求解算法是一种有效的正交多项式求根方法。
《4 结语 》
4 结语
研究了高次勒让德多项式、拉盖尔多项式和厄米多项式的高精度根的数值求解方法。先对拉盖尔多项式、厄米多项式的定义稍做变化后,获得了计算多项式值的稳定递推关系。通过搜索-迭代算法,先在一定的根范围内搜索到多项式所有的根区间,再以常用的迭代求根方法如割线法、二分法或牛顿法等进行求解,可获得所需精度的根。在获得高精度的正交多项式的根后,可给出高次高斯积分的积分节点和积分权重因子。














 京公网安备 11010502051620号
京公网安备 11010502051620号




