抛物形缓坡方程的数值研究

摘要

对2种典型的抛物形缓坡方程进行比较系统的数值研究。通过对4种典型地形上的波浪变形的数值模拟，详细讨论了网格节点数对数值解精度的影响、模型对初始入射角的敏感程度、非线性项对数值结果的影响等。研究结果可为实际应用抛物形缓坡方程研究大区域复杂地形上的波浪传播提供一定的理论指导。

正文

《1 前言》

1 前言

抛物形缓坡方程由Radder^[1] 首次提出, 是研究波浪变形的一类有效数学模型。它们综合考虑了由于地形变化或障碍物作用而引起的波浪折射、绕射及浅化效应, 在理论上比射线理论先进, 在数值求解方面比椭圆型缓坡方程简单得多, 此外它们与射线理论一样, 可以用于较大区域的波浪变形预报。该类模型的最大缺点是波浪必须沿某一主要方向传播, 也就是所谓的小角度限制, 尽管一些学者采用极值原理^[2]、付立叶变换^[3,4] 和保角变换^[5] 对这一限制进行了一定程度的弥补, 但这3个模型仍存在角度限制, 而且模型本身及数值求解比弥补前的方程要复杂得多。除受入射角度的限制外, 该类模型难以考虑主传播方向上的波浪反射, 这也是抛物形缓坡方程不尽人意的地方, 但总体说来, 抛物形缓坡方程的优越性超过其限制, 其精度可以满足工程实际需要, 因而应用较广。由于高阶和保角变换模型本身或求解方法比较复杂, 因此只对小角度和极值原理抛物形缓坡方程进行比较系统的数值研究, 并对4种典型的实验或假想地形进行波浪变形的数值模拟, 以对这两种抛物形缓坡方程有比较全面的认识。

《2 数学模型》

2 数学模型

《2.1抛物形缓坡模型的基本控制方程》

2.1抛物形缓坡模型的基本控制方程

《2.1.1 小角度抛物形缓坡方程小角度线性抛物形缓坡方程为》

2.1.1 小角度抛物形缓坡方程小角度线性抛物形缓坡方程为

$\frac{\partial A}{\partial x} = [i (k - \bar{k}) - \frac{1}{2 F} \frac{\partial F}{\partial x}] A + \frac{i}{2 F} \frac{\partial}{\partial y} (E \frac{\partial A}{\partial y}) ‚ (1)$ $\frac{\partial A}{\partial x} = [i (k - \bar{k}) - \frac{1}{2 F} \frac{\partial F}{\partial x}] A + \frac{i}{2 F} \frac{\partial}{\partial y} (E \frac{\partial A}{\partial y}) ‚ (1)$

式中A为与时间无关的复振幅, k为波数, $\bar{k}$ $\bar{k}$ 为纵轴方向 (y方向) 上k的平均值, F=kCC_g, E=CC_g, C=ω/k为波相速, ω为波浪角频率, C_g为波群速, x为波浪传播的主方向, y为纵轴方向, $i = \sqrt{- 1}$ $i = \sqrt{- 1}$ 。对非线性波浪传播问题, Kirby和Dalrymple^[6] 给出了弱非线性Stokes波传播的抛物形缓坡方程

$\begin{array}{l} \frac{\partial A}{\partial x} = [i (k - \bar{k}) - \frac{1}{2 F} \frac{\partial F}{\partial x}] A + \\ \frac{i}{2 F} \frac{\partial}{\partial y} (E \frac{\partial A}{\partial y}) - i \frac{D}{2} | A |^{2} A 。 (2) \end{array}$ $\begin{array}{l} \frac{\partial A}{\partial x} = [i (k - \bar{k}) - \frac{1}{2 F} \frac{\partial F}{\partial x}] A + \\ \frac{i}{2 F} \frac{\partial}{\partial y} (E \frac{\partial A}{\partial y}) - i \frac{D}{2} | A |^{2} A 。 (2) \end{array}$

式 (2) 中的最后一项为非线性作用项, 也是式 (2) 与式 (1) 唯一不相同的地方, 系数D为

$D = k^{3} \frac{C}{C_{g}} \frac{\cosh 4 k d + 8 - 2 \tanh^{2} k d}{8 \sinh^{4} k d},$ $D = k^{3} \frac{C}{C_{g}} \frac{\cosh 4 k d + 8 - 2 \tanh^{2} k d}{8 \sinh^{4} k d},$

其中d为静水深。

《2.1.2 极值原理抛物形缓坡方程极值原理抛物形缓坡方程为[2]》

2.1.2 极值原理抛物形缓坡方程极值原理抛物形缓坡方程为[2]

$\begin{array}{l} C_{g} \frac{\partial A}{\partial x} = [E^{'} + \frac{1}{2} \frac{\partial C_{g}}{\partial x}] A - \\ \frac{b_{1}}{ω k} \frac{\partial^{2}}{\partial x \partial y} (E \frac{\partial A}{\partial y}) + F^{'} \frac{\partial}{\partial y} (E \frac{\partial A}{\partial y}) = 0, (3) \end{array}$ $\begin{array}{l} C_{g} \frac{\partial A}{\partial x} = [E^{'} + \frac{1}{2} \frac{\partial C_{g}}{\partial x}] A - \\ \frac{b_{1}}{ω k} \frac{\partial^{2}}{\partial x \partial y} (E \frac{\partial A}{\partial y}) + F^{'} \frac{\partial}{\partial y} (E \frac{\partial A}{\partial y}) = 0, (3) \end{array}$

其中 $E^{'} = i (\bar{k} - a_{0} k) C_{g} + \frac{i C_{g}}{2} D | A |^{2}$ $E^{'} = i (\bar{k} - a_{0} k) C_{g} + \frac{i C_{g}}{2} D | A |^{2}$ ; $F^{'} = \frac{i}{ω} (a_{1} - b_{1} \frac{\bar{k}}{k}) + \frac{b_{1}}{ω} [\frac{k_{x}}{k^{2}} + \frac{(C_{g})_{x}}{2 k C_{g}}]$ $F^{'} = \frac{i}{ω} (a_{1} - b_{1} \frac{\bar{k}}{k}) + \frac{b_{1}}{ω} [\frac{k_{x}}{k^{2}} + \frac{(C_{g})_{x}}{2 k C_{g}}]$ ;a₀, a₁, b₁为根据最大可偏离主传播方向的角度θ_a而确定的系数, 其他变量的含义同前。

采用有限差分法对式 (2) 和式 (3) 进行离散, 得到的离散格式见文献[7]。离散得到的代数方程组可采用有关线性或非线性方程组的数值方法求解, 从而得到计算域内的波要素分布。

《2.2抛物形缓坡方程的边界条件》

2.2抛物形缓坡方程的边界条件

《2.2.1 入射边界条件》

2.2.1 入射边界条件

入射边界条件可由实测值给出或者由某一简单的代数式确定, 对入射速度势φ (x₀, y) =A₀exp i (kcos α₀x₀+ksin α₀y) 的微幅波, 可以给定

$A (x_{0}, y) = A_{0} \exp i [(k - \bar{k}) \cos α_{0} x_{0} + k s i n α_{0} y], (4)$ $A (x_{0}, y) = A_{0} \exp i [(k - \bar{k}) \cos α_{0} x_{0} + k s i n α_{0} y], (4)$

其中A₀为入射波振幅 (实数) , α₀为初始入射波向, x₀为入射位置坐标。

《2.2.2 侧边界条件及其数值实现》

2.2.2 侧边界条件及其数值实现

侧向边界条件主要有全反射、开放和部分反射3种侧边界条件, 它们分别由∂A/∂y=0.∂A/∂y=ikAsin α和∂A/∂y=iC_akAsin α给出, 其中C_a为吸收系数, 需预先确定;α为侧边界处的波向角, 由于其预先未知, 所以在数值离散时需要作特别处理。全反射边界条件的离散比较简单, 而开放和部分反射边界条件的离散见文献[2,8]。

《3 算例及结果分析》

3 算例及结果分析

《3.1平底上的波浪绕射》

3.1平底上的波浪绕射

进行平底上的波浪绕射数值试验的目的主要有两方面: a.当地形为平底时, 可得到抛物形缓坡方程式 (2) 和式 (3) 对应的线性方程的解析解, 将数值解与解析解进行对比, 就可对数值格式的精度有定量的了解;b.抛物形缓坡方程的较大优点是可用于较大区域, 即每个波长的空间范围需要布置的网格节点可以较少。通过对每个波长布置不同的节点数, 然后将数值解与解析解比较, 就可以定量地得到抛物形缓坡方程每个波长需布置的合适节点数。

假定计算域长2.1 km, 宽1.4 km, 水深为10 m, 入射波表示为

$A (x_{0}, y) = 0.5 \exp i [(k - \bar{k}) \cos α_{0} x_{0} + k s i n α_{0} y] ‚$ $A (x_{0}, y) = 0.5 \exp i [(k - \bar{k}) \cos α_{0} x_{0} + k s i n α_{0} y] ‚$

其中波周期为8 s, 在该地形下对应的入射波长λ约为70.85 m (由线性波的色散关系得出) , 初始入射位置x₀=0, 初始入射波向与x轴的夹角为20°。

《3.1.1 线性抛物形方程的数值解、解析解和真实解间的对比》

3.1.1 线性抛物形方程的数值解、解析解和真实解间的对比

对于前面给出的地形和入射波要素, 计算域内的波浪复振幅A的分布 (真实解) 为

$A (x, y) = 0.5 \exp i [(k - \bar{k}) \cos α_{0} x + k s i n α_{0} y] ‚ (5)$ $A (x, y) = 0.5 \exp i [(k - \bar{k}) \cos α_{0} x + k s i n α_{0} y] ‚ (5)$

而此时式 (2) 对应的线性方程的解析解形式为

$A (x, y) = 0.5 \exp i [β x + k s i n α_{0} y] ‚ (6)$ $A (x, y) = 0.5 \exp i [β x + k s i n α_{0} y] ‚ (6)$

式中, β=- (ksinα₀) ²/ (2k) 。而式 (3) 的线性方程的解析解为

$A (x, y) = 0.5 \exp i [β_{1} x + k s i n α_{0} y] ‚ (7)$ $A (x, y) = 0.5 \exp i [β_{1} x + k s i n α_{0} y] ‚ (7)$

式中,

$β_{1} = \frac{k (a_{0} - 1) - (k s i n α_{0})^{2} (b_{1} - a_{1}) / k}{1 + b_{1} (k s i n α_{0})^{2} / k^{2}}$ $β_{1} = \frac{k (a_{0} - 1) - (k s i n α_{0})^{2} (b_{1} - a_{1}) / k}{1 + b_{1} (k s i n α_{0})^{2} / k^{2}}$

上式中a₀, a₁, b₁按θ_a=70°取值^[2], 这样取值是为了使极值原理模型能适用于较大角度。数值计算采用的空间步长为Δx=Δy=7m≈0.1λ, 即每个波长布置10个节点, 仅选取2个典型断面的结果进行比较, 这2个断面的线性抛物形缓坡方程的数值结果、解析解和真实解如图1和图2所示。图中纵坐标的Re A表示复振幅A的实部。从这2组图中可以看出, 当初始入射波向为20°的简单波在平底地形上传播时, 如果每个波长布置10个网格点, 则2种线性抛物形缓坡方程的数值解均和它们对应的解析解几乎重合, 与真实解十分接近。总体上看, 极值原理模型的解 (包括解析解和数值解) 更接近真实解。该结果表明在网格点较密的情况下, 数值解能很好的反映解析解, 说明了数值格式的良好性能。

《图1》

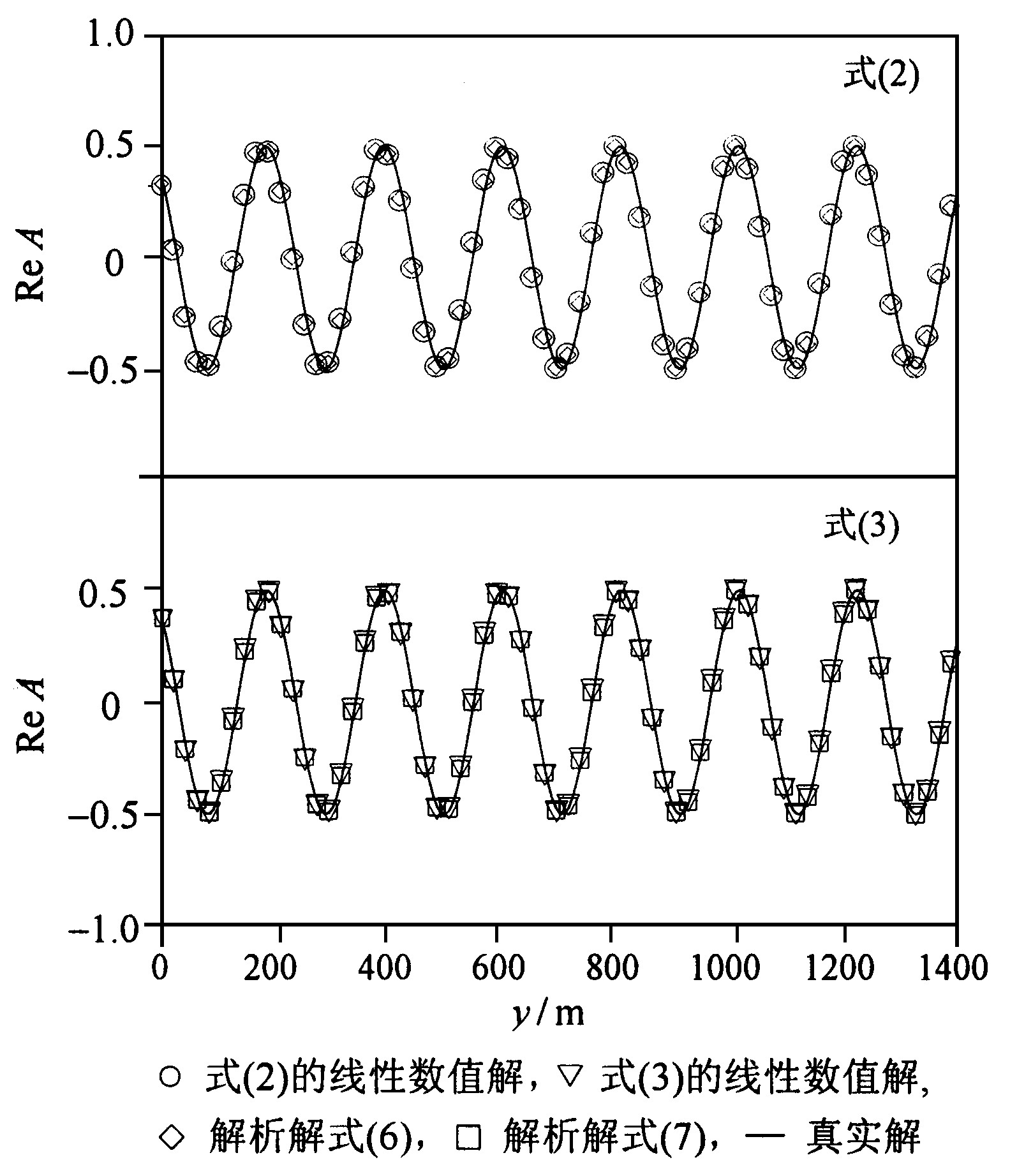
图1 断面1 (x=1 050 m) 处式 (2) 和式 (3) 的线性数值解、解析解和真实解

Fig.1 Numerical, analytical and real solutionsof eqs. (1) and (2) at section 1 (x=1 050 m)

《图2》

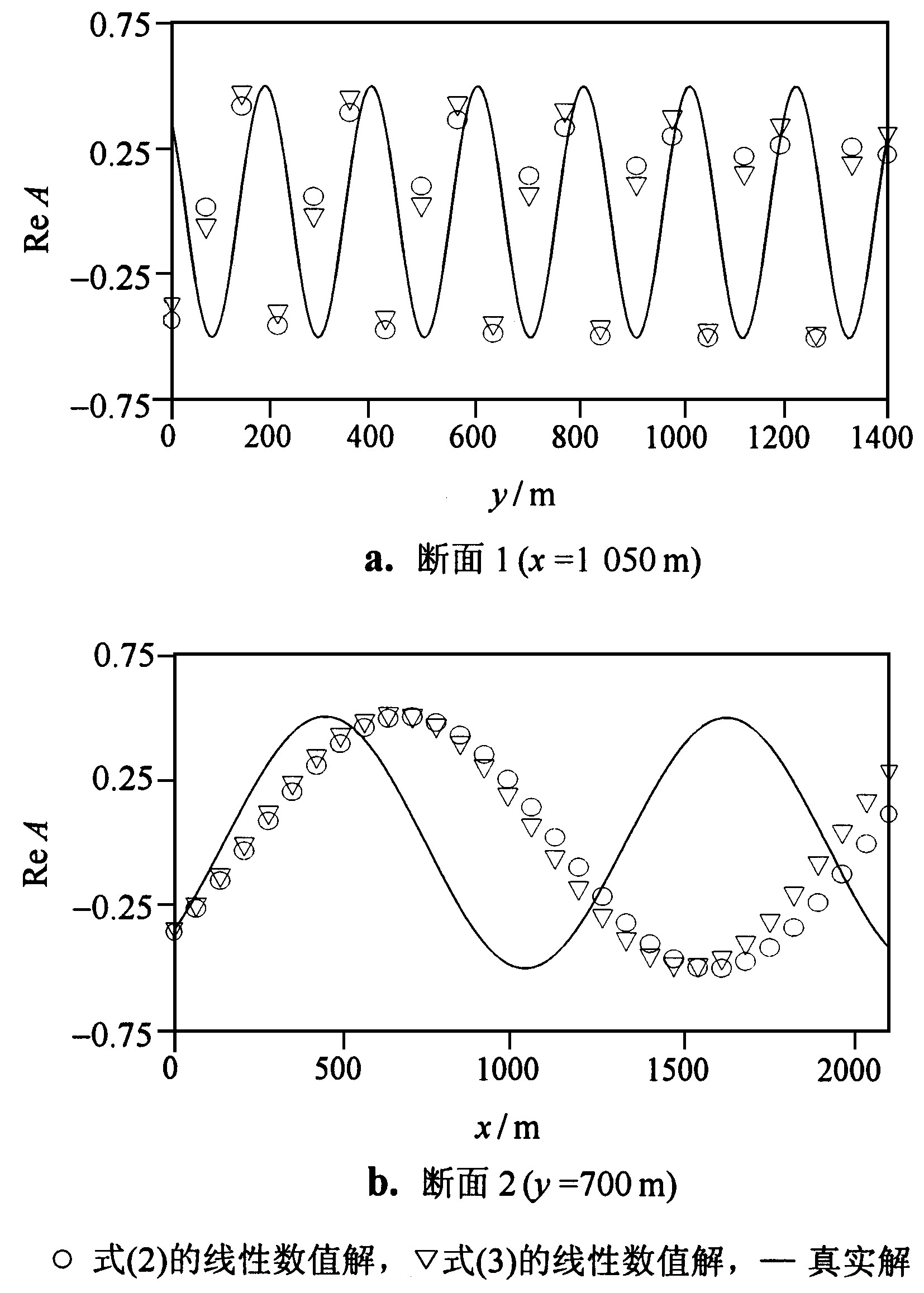
图2 断面2 (y=700 m) 处式 (2) 和式 (3) 的线性数值解、解析解和真实解

Fig.2 Numerical, analytical and real solutionsof eqs. (1) and (2) at section 1 (y=700 m)

《3.1.2 网格节点数对数值解精度的影响》

3.1.2 网格节点数对数值解精度的影响

对前节的平底地形上的波浪传播, 讨论2种不同的节点布置:a.Δx=Δy=70 m, 即每个波长布置1个节点;b.Δx=Δy=35 m, 即每个波长布置2个节点。图3a和图3b分别为每个波长布置1个节点时2个断面对应的数值解与真实解的比较, 可以看出, 抛物形缓坡方程在每个波长布置1个节点时, 采用文献[7]的数值格式得到的数值解的精度相当差;图4a和图4b分别为每个波长布置2个节点时2个断面对应的数值解与真实解的比较, 可以看出数值解尽管存在一定误差, 但比每个波长布置1个节点时得到的数值解有了相当大的改善, 这也是为什么抛物形缓坡方程每个波长只需要布置约3个节点的原因。当然如果实际地形复杂, 则每个波长所需布置的节点数应以能够分辨地形的变化为准, 这样才能准确地预报地形引起的波浪变形。

《图3》

图3 每波长1个节点的数值解和真实解

Fig.3 Numerical and real solutions with one point per wavelength

《图4》

图4 每波长2个节点的数值解和真实解

Fig.4 Numerical and real solution with two point per wavelength

《3.2直平行等深线上的波浪折射》

3.2直平行等深线上的波浪折射

直平行等深线地形是一种理想化的有变化地形, 波浪在其上传播会发生折射和浅化效应, 并且在波浪破碎前, 对这种地形波要素存在精确解, 因此采用抛物形缓坡方程研究波浪在该类地形上发生的变形, 可以考察在不同的初始入射角下, 抛物形缓坡方程对波浪折射和浅化作用的预报准确程度。所采用的计算要素和前面平底上的大致相同, 不同的是沿x方向有水深变化, 即

$d (x, y) = 10 - x / 300 (m) 。$ $d (x, y) = 10 - x / 300 (m) 。$

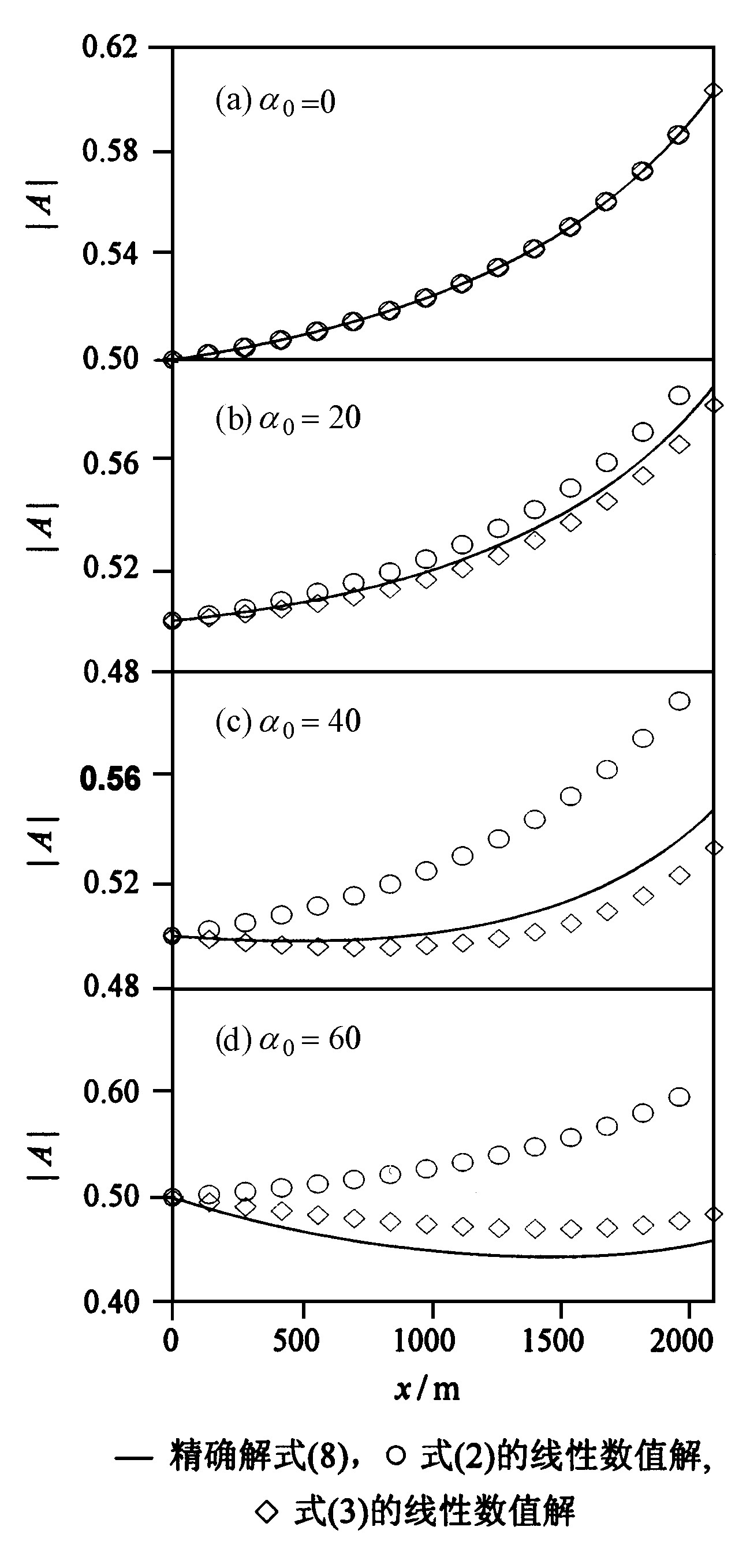
此时入射波长为70.85 m, 而水深最浅处的波长为41.85 m。考虑4种不同的初始入射波向, 即α₀=0°, 20°, 40°, 60°。数值计算采用的空间步长对不同的初始入射角均为Δx=Δy=14 m。对该种地形, 波振幅的精确解为

$| A | = A_{0} [\frac{k c o s α_{0}}{k_{0} \cos α} \frac{1 + \frac{2 k_{0} d_{0}}{\sinh 2 k_{0} d_{0}}}{1 + \frac{2 k d}{\sinh 2 k d}}]^{1 / 2} ‚ (8)$ $| A | = A_{0} [\frac{k c o s α_{0}}{k_{0} \cos α} \frac{1 + \frac{2 k_{0} d_{0}}{\sinh 2 k_{0} d_{0}}}{1 + \frac{2 k d}{\sinh 2 k d}}]^{1 / 2} ‚ (8)$

其中下标0表示入射位置的量, 任意位置的波向α由ksin α=k₀sin α₀确定。

图5a为初始入射角为0°时的几种结果比较, 此时小角度模型和极值原理模型的数值结果均和精确解完全重合。图5b为初始入射角为20°时的各种结果比较, 此时极值原理模型的结果与精确解相比偏小, 而小角度模型的数值结果偏大, 总体上此时小角度模型的结果比极值原理模型的结果差。图5c为初始入射角为40°时的各种结果比较, 此时极值原理模型的结果和精确解之间的偏差进一步加大, 而小角度模型的结果偏大, 最大相对偏差约10 %, 因此为了保证精度, 在初始入射角大于40°时, 最好不要采用小角度模型。图5d为初始入射角为60° 时的结果比较, 此时极值原理模型的数值结果也发生了较大偏差, 此时应用极值原理模型研究波浪变形需慎重。

《图5》

图5 直平行等深线地形上波振幅的数值解和精确解的比较

Fig.5 Comparison of numerical results with analytical solutions

《3.3复杂地形上的波浪折绕射》

3.3复杂地形上的波浪折绕射

对2种典型的比较复杂的地形上波浪变形的数值模拟来研究弱非线性抛物形缓坡方程。

《3.3.1 圆形浅滩上的波浪折绕射》

3.3.1 圆形浅滩上的波浪折绕射

Zheng等^[9] 对这种地形及入射波要素进行了详细介绍, 这里仅给出2种抛物形缓坡方程的数值计算结果。数值计算的空间步长为Δx=Δy=0.1 m, 即在水深最浅处 (此时由线性频散关系得到的波长λ≈0.31 m) 每个波长布置3个节点。

图6a至图6c分别为3个断面的数值解与实测值的比较, 图中纵坐标|A|/A₀表示计算或实测的波振幅与入射波振幅的比值, 其中|A|表示计算或实测的振幅, A₀表示入射波振幅。比较结果可以看出:a.极值原理模型和小角度模型的数值差别很小;b.极值原理和小角度线性抛物形缓坡模型的数值均和实测值比较吻合, 而它们对应的非线性模型的结果均呈现偏小趋势。

《图6》

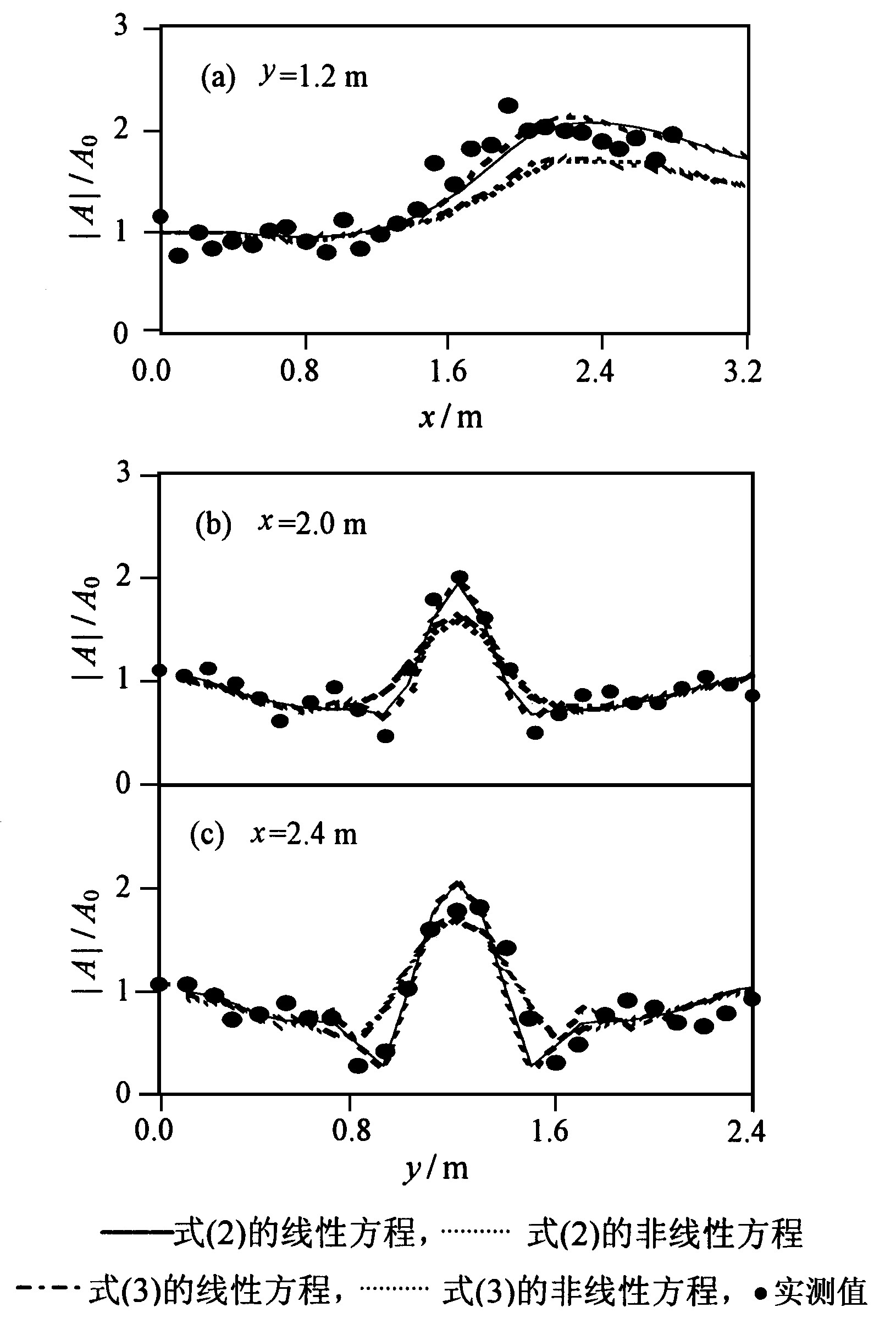
图6 圆形浅滩地形上比振幅的数值解与实测值比较

Fig.6 Comparison of numerical results with experimental data over a circular shoal

《3.3.2 椭圆形浅滩上的波浪折绕射》

3.3.2 椭圆形浅滩上的波浪折绕射

Zheng等^[9] 对这种地形及入射波要素进行了详细介绍, 这里仅给出2种抛物形缓坡方程的数值结果, 计算的空间步长为Δx=Δy=0.25 m, 即在水深最浅处 (此时由线性频散关系得到的波长λ≈0.7 m) 每个波长布置3个多节点。图7a至图7h分别为8个断面的实测值和2种线性抛物形缓坡模型的数值解的对比, 可以看出:a.小角度模型和极值原理模型的数值存在微小差别, 在某些断面上甚至分布趋势也不完全相同;b. 2种抛物形缓坡方程的线性数值结果均与实测值存在较大差别, Kirby和Dalrymple^[6] 认为这是由于没有考虑非线性影响的缘故。图8a至图8h分别为8个断面的实测值和2种非线性抛物形缓坡模型的数值解的对比, 可以看出:a. 2种非线性抛物形缓坡模型的数值解均和实测值十分接近;b. 2种抛物形缓坡方程的非线性数值结果差别很小, 但从总体上看, 极值原理模型的非线性数值结果和实测值吻合更好;c.数值结果表明非线性模型优于线性模型, 而前面圆形浅滩的算例表明线性模型优于非线性模型, 从这算例的结果看, Kirby和Dalrymple^[6] 认为非线性模型更优越的结论仍需要做进一步的验证。

《图7》

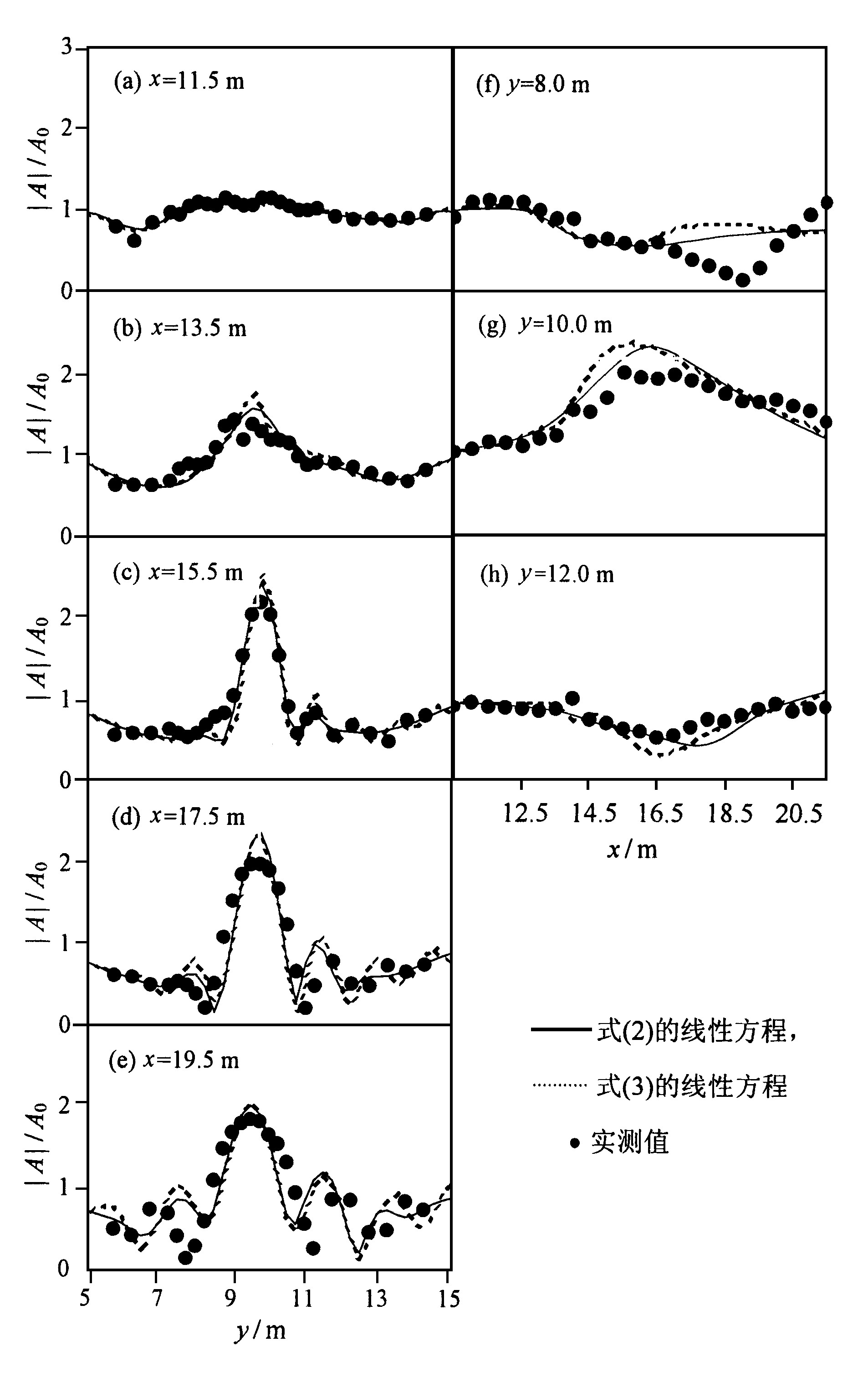
图7 线性抛物形缓坡方程的数值解与实测值比较

Fig.7 Comparison of numerical results by the linear parabolic equations with experimental data

《4 结语》

4 结语

为了合理地应用抛物形缓坡模型, 对2种典型的抛物形缓坡方程进行系统的数值研究。通过对4种典型地形上的波浪变形的数值模拟, 详细讨论了数值格式的精度、网格节点数对数值解精度的影响、模型对初始入射角的敏感程度、非线性项对数值结果的影响等。研究结果可为实际应用抛物形缓坡方程研究大区域复杂地形上的波浪传播提供一定的理论指导。

《图8》

图8 非线性抛物形缓坡方程的数值解与实测值比较

Fig.8 Comparison of numerical results by the non-linear parabolic equations with experimental data

展示更多