用考虑置信区间长度影响的最小二乘法拟合S-N曲线

摘要

S-N曲线是用名义应力法预测结构疲劳寿命的基础。基于试验疲劳寿命分散的物理机制，提出了一个S-N曲线试验数据处理的加权最小二乘法，此方法中每组数据的权重与该组数据的置信区间成反比。计算结果表明用考虑置信区间长度影响的最小二乘法拟合得到的S-N曲线比用一般最小二乘法得到的S-N曲线具有更高的可靠度，给出的寿命预测结果也更安全。

正文

《1 引言》

1 引言

在疲劳研究的100多年历史中, 尽管已发展了多种疲劳寿命研究方法, 但在工程实践中, 各种各样的修改的名义应力法仍然得到了广泛应用, 而S-N曲线是用名义应力法估算疲劳寿命的基础。在疲劳可靠性设计和疲劳性能测试中, 常用的S-N曲线表达式有双参数幂函数表达式、指数函数表达式和三参数幂函数表达式 ^[1]。需要指出, 上述所有的S-N曲线均是对实验数据的拟合曲线, 拟合的方法一般为对一组疲劳试验数据的均值进行最小二乘拟合。

大量的实验数据表明, 疲劳寿命一般服从对数正态分布。文献[1]中正态母体疲劳寿命均值的区间估计为

$\bar{x} - t_{γ} s / n^{1 / 2} < μ < \bar{x} + t_{γ} s / n^{1 / 2} (1)$ $\bar{x} - t_{γ} s / n^{1 / 2} < μ < \bar{x} + t_{γ} s / n^{1 / 2} (1)$

式中μ为正态母体均值, $\bar{x}$ $\bar{x}$ 为样本均值, s为样本标准差, γ为置信度, n为试件个数。式 (1) 表明以γ的置信度, 因此置信区间 $\bar{x} - t_{γ} s / n^{1 / 2} ‚ \bar{x} + t_{γ} s / n^{1 / 2}$ $\bar{x} - t_{γ} s / n^{1 / 2} ‚ \bar{x} + t_{γ} s / n^{1 / 2}$ 包含μ值。置信区间越小, 当拟合S-N曲线时, 样本均值 $\bar{x}$ $\bar{x}$ 作为拟合点的可靠度越高, 反之则越低。

但在常规的最小二乘法拟合S-N曲线时, 却没有考虑置信区间长度的影响。图1中×表示实验数据的样本均值点, 横线段表示置信度γ下实验数据均值的置信区间长度。

《图1》

图1最小二乘法拟合实验数据示意图Fig.1 The least square fit of test data

由图1可见, 尽管S₃<S₅, 拟合曲线却更靠近5点, 但在曲线拟合时总希望拟合曲线靠近置信区间短的点。

《2 用加权最小二乘法拟合实验数据的一般方法》

2 用加权最小二乘法拟合实验数据的一般方法

已知实验数据组 (x_i, y_i) (i=1, 2, 3, …, n) , 现有函数f (x) 使得

$∥ (y_{i} - f (x_{i})) ∥_{2} = [\sum_{i = 1}^{n} (y_{i} - f (x_{i}))^{2}]^{1 / 2} = \min (2)$ $∥ (y_{i} - f (x_{i})) ∥_{2} = [\sum_{i = 1}^{n} (y_{i} - f (x_{i}))^{2}]^{1 / 2} = \min (2)$

式 (2) 可改写为

$\sum_{i = 1}^{n} (y_{i} - f (x_{i}))^{2} = \min (3)$ $\sum_{i = 1}^{n} (y_{i} - f (x_{i}))^{2} = \min (3)$

令

$Q = \sum_{i = 1}^{n} [y_{i} - f (x_{i})]^{2} (4)$ $Q = \sum_{i = 1}^{n} [y_{i} - f (x_{i})]^{2} (4)$

设函数f (x) 中含有k个待定系数a_k (k<n) 则

$\begin{array}{l} \frac{\partial Q}{\partial a_{j}} = \sum_{i = 1}^{n} [y_{i} - f (x_{i})] \frac{\partial f (x)}{\partial a_{j}} |_{x = x_{i}} = 0 \\ (j = 1, 2, \dots, k) (5) \end{array}$ $\begin{array}{l} \frac{\partial Q}{\partial a_{j}} = \sum_{i = 1}^{n} [y_{i} - f (x_{i})] \frac{\partial f (x)}{\partial a_{j}} |_{x = x_{i}} = 0 \\ (j = 1, 2, \dots, k) (5) \end{array}$

解上述正规方程组, 便可确定k个待定系数a_k。

不难看出上述最小二乘拟合问题也是求解关于a_k (k<n) 的超定方程组

$f (x_{i}) = y_{i} (i = 1, 2, 3, \dots) (6)$ $f (x_{i}) = y_{i} (i = 1, 2, 3, \dots) (6)$

的最小二乘解问题。

如果采用多项式拟合, 即

$f (x_{i}) = \sum_{i = 0}^{m} a_{i} x^{i} (7)$ $f (x_{i}) = \sum_{i = 0}^{m} a_{i} x^{i} (7)$

则方程组的矩阵计法为

$A X = b (8)$ $A X = b (8)$

其中:

$\begin{array}{l} b = [y_{0}, y_{1}, \dots, y_{n}]^{Τ} ‚ \\ X = [a_{0}, a_{1}, \dots, a_{n}]^{Τ} ‚ \\ A = [\begin{matrix} 1 & x_{0} & x_{0}^{2} & \dots & x_{0}^{m} \\ 1 & x_{1} & x_{1}^{2} & \dots & x_{1}^{m} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ 1 & x_{n} & x_{n}^{2} & \dots & x_{n}^{m} \end{matrix}] ‚ \end{array}$ $\begin{array}{l} b = [y_{0}, y_{1}, \dots, y_{n}]^{Τ} ‚ \\ X = [a_{0}, a_{1}, \dots, a_{n}]^{Τ} ‚ \\ A = [\begin{matrix} 1 & x_{0} & x_{0}^{2} & \dots & x_{0}^{m} \\ 1 & x_{1} & x_{1}^{2} & \dots & x_{1}^{m} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ 1 & x_{n} & x_{n}^{2} & \dots & x_{n}^{m} \end{matrix}] ‚ \end{array}$

由矩阵理论可知, 不相容方程组式 (8) 的一般最小二乘解为

$X = A_{l}^{- 1} b (9)$ $X = A_{l}^{- 1} b (9)$

其中广义逆A $_{l}^{- 1}$ $_{l}^{- 1}$ 为

$A_{l}^{- 1} = (A^{*} A)^{- 1} A^{*} ‚$ $A_{l}^{- 1} = (A^{*} A)^{- 1} A^{*} ‚$

而加权最小二乘解为

$X = A_{l w}^{- 1} b (10)$ $X = A_{l w}^{- 1} b (10)$

式中A $_{l w}^{- 1}$ $_{l w}^{- 1}$ 为加权的最小二乘广义逆

$A_{l w}^{- 1} = (A^{*} W A)^{- 1} A^{*} W (11)$ $A_{l w}^{- 1} = (A^{*} W A)^{- 1} A^{*} W (11)$

式中W为对称正定矩阵, 在实际问题中也可称为加权矩阵。

《3 考虑置信区间长度影响的S-N曲线拟合》

3 考虑置信区间长度影响的S-N曲线拟合

《3.1 权重wi》

3.1 权重wi

引入权重

$w_{i} = w / d_{i}^{p} (12)$ $w_{i} = w / d_{i}^{p} (12)$

式中d_i为第i个应力水平下的试验值的置信区间的长度, 按式 (1) 计算;p为敏感指数, 不妨取1;w为常数, 由归一化方程确定。

$\begin{array}{l} d_{i} = 2 t_{γ} S_{i} / n_{i}^{1 / 2} (13) \\ \sum_{i = 1}^{n} \frac{w}{d_{i}} = 1 (14) \end{array}$ $\begin{array}{l} d_{i} = 2 t_{γ} S_{i} / n_{i}^{1 / 2} (13) \\ \sum_{i = 1}^{n} \frac{w}{d_{i}} = 1 (14) \end{array}$

于是权重为

$w_{i} = 1 / d_{i}^{p} \cdot \sum_{i = 1}^{n} 1 / d_{i} (15)$ $w_{i} = 1 / d_{i}^{p} \cdot \sum_{i = 1}^{n} 1 / d_{i} (15)$

因此, 加权矩阵W为

$W = [\begin{matrix} w_{1} & 0 & \dots & 0 \\ 0 & w_{2} & \dots & 0 \\ ⋮ & ⋮ & ⋮ \\ 0 & 0 & \dots & w_{n} \end{matrix}] (16)$ $W = [\begin{matrix} w_{1} & 0 & \dots & 0 \\ 0 & w_{2} & \dots & 0 \\ ⋮ & ⋮ & ⋮ \\ 0 & 0 & \dots & w_{n} \end{matrix}] (16)$

式中w_i由公式 (14) 确定。

如果S-N曲线用幂函数的形式表示:

$S_{a}^{m} Ν = C (17)$ $S_{a}^{m} Ν = C (17)$

对式 (17) 两边取对数得

$Μ \lg S_{a} + \lg Ν = \lg C (18)$ $Μ \lg S_{a} + \lg Ν = \lg C (18)$

上式可改写成

$\lg Ν \times x_{1} + x_{2} = \lg S_{a} (19)$ $\lg Ν \times x_{1} + x_{2} = \lg S_{a} (19)$

对于n个试验数据点 (S $_{a}^{i}$ $_{a}^{i}$ , Nⁱ) , 式 (19) 为超定方程组, 用矩阵形式表示为

$A X = b (20)$ $A X = b (20)$

式中

$\begin{array}{l} A = [\begin{matrix} \lg Ν_{1} & 1 \\ \lg Ν_{2} & 1 \\ ⋮ & ⋮ \\ \lg Ν_{n} & 1 \end{matrix}] ‚ \\ X = [\begin{array}{l} x_{1} \\ x_{2} \end{array}] ‚ \\ b = [\begin{array}{l} \lg (S_{a}^{(1)}) \\ \lg (S_{a}^{(2)}) \\ ⋮ \\ \lg (S_{a}^{(n)}) \end{array}] 。 \end{array}$ $\begin{array}{l} A = [\begin{matrix} \lg Ν_{1} & 1 \\ \lg Ν_{2} & 1 \\ ⋮ & ⋮ \\ \lg Ν_{n} & 1 \end{matrix}] ‚ \\ X = [\begin{array}{l} x_{1} \\ x_{2} \end{array}] ‚ \\ b = [\begin{array}{l} \lg (S_{a}^{(1)}) \\ \lg (S_{a}^{(2)}) \\ ⋮ \\ \lg (S_{a}^{(n)}) \end{array}] 。 \end{array}$

于是, 考虑置信区间长度影响的加权最小二乘解便可用式 (11) 表示。

《3.2 算例》

3.2 算例

LY12CZ铝合金包铝板材 (轴向加载) 试验原始数据如表1所示 ^[2]。

表1 试验原始数据Table 1 The original test data

《图2》

*95%置信度下的置信区间长度

对表1中的数据分别进行最小二乘拟合与加权的最小二乘拟合, 结果如图2和图3所示。

《图3》

图2 K_t=1时S-N曲线Fig.2 The least square fit of S-N curve

《4 结果讨论》

4 结果讨论

1) 图2中, 置信区间的长度随着疲劳次数的增加而增加, 一般最小二乘法拟合的结果和期望的正好相反。如图2中4点的置信区间长度最大 (分散性最大) 却离所拟合的直线最近, 1点的置信区间长度最短却离所拟合的直线最远, 而考虑置信区间长度影响的最小二乘法所拟合的直线基本符合期望:1点的置信区间长度最短离所拟合的直线最近, 4点的置信区间长度最远, 离所拟合的直线也最远。因此, 考虑置信区间长度影响的最小二乘法得到的S-N曲线比一般最小二乘法得到的S-N曲线有更高的可靠度。

《图4》

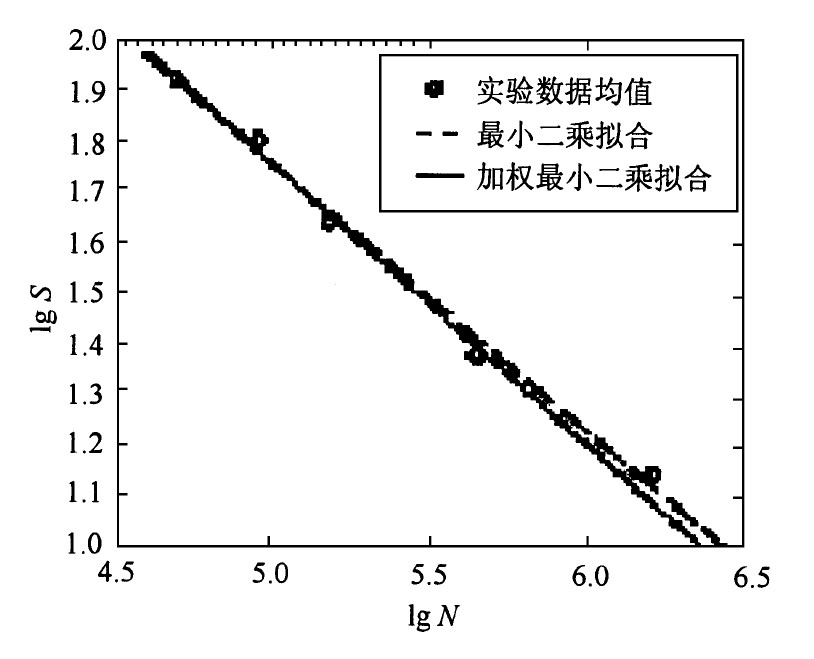
图3 K_t=2.5时S-N曲线Fig.3 The least square fit of S-N curve

2) 在用名义应力法估算结构寿命时, S-N曲线的形状严重地影响寿命估算的结果。疲劳寿命的分散性一般随着疲劳寿命的增加而增加, 由图2、图3可知, 用一般最小二乘法得到的S-N曲线比用考虑置信区间长度影响的最小二乘法得到的S-N曲线更趋近于寿命长的实验数据点, 造成预测寿命偏于危险, 而用考虑置信区间长度影响的最小二乘法得到的S-N曲线进行寿命预测则偏于安全。

展示更多