《1 前言》
1 前言
对于非线性系统控制, 一般首先采用线性化的方法[1,2], 再用其他控制手段进行控制[3,4,5]。在系统状态未知的情况下, 通常的观测器不能同时观测其外部及内模动态[6,7]。而一般的滑模控制器具有抖振现象[8,9], 加入饱和函数后可以消除抖振现象, 却导致收敛速度与精度降低[10,11]。连续形式的滑模控制可以消除抖振[12]。文献[13]中提出了基于一阶微分方程的解在有限时间内到达零并保持不变特性的滑动模态, 而滑模面为多层结构, 随着滑动变量沿滑模面逐层滑动, 变量最后达到零, 降低了抖振现象。然而, 控制器中含有滑模变量的高阶导数, 当存在不确定性和扰动情况时, 每层的滑模变量都将受到不确定性与扰动的影响。利用一个基于非线性系统线性化的观测器, 同时观测外部及内模动态变量, 并引入一层滑模面和具有滤波形式的摄动参数的滑模变量, 既能够消除抖振现象, 同时保证系统状态变量迅速收敛。
《2 问题分析》
2 问题分析
{x˙=f(x)+g(x)u,y=h(x)。 (1)
其中, x为n维状态变量, f (x) , g (x) 是n维光滑向量函数。u∈R是控制输入, y为输出。设系统的相对阶为r, 即满足如下关系:
LgLi−1fh(x)=0, i=1,2,⋯,r−1,LgLr−1fh(x)≠0
⎧⎩⎨⎪⎪ξ˙=Aξ+B[a(ξ,η)+b(ξ,η)u],η˙=q(ξ,η),y=CTξ。 (2)
[ξ η]T=[ξ1⋯ξrη1⋯ηn−r]T,χ(x)=[h(x) Lfh(x) ⋯ Lr−1fh(x)χ1(x) ⋯ χn−r(x)]‚a(ξ‚η)=Lrfh(χ−1(ξ‚η)),b(ξ‚η)=LgLr−1fh(χ−1(ξ‚η))≠0,A=⎡⎣⎢⎢⎢⎢00⋮010⋮001⋮0⋯⋯ ⋯00⋮0⎤⎦⎥⎥⎥⎥r×r‚B=⎡⎣⎢⎢⎢⎢0⋮01⎤⎦⎥⎥⎥⎥r×1‚C=⎡⎣⎢⎢⎢⎢10⋮0⎤⎦⎥⎥⎥⎥r×1。 (3)
令e=y−yΓ,e¯=[e1⋯er]T=[ξ1−yΓ⋯ξr−11−yr−1Γ]T‚YΓ=[yΓ⋯y(r−1)Γ]T。yΓ为参考输出。所以, 误差系统为
⎧⎩⎨e∸=Ae¯+B[a(e¯,η,YΓ)−Y(r)Γ+b(e¯,η,YΓ)u],η˙=q(e¯,η,YΓ)。 (4)
假设1 内模动态η˙=q(0,η,0)对于原点是局部指数稳定的 (对于物理系统而言, 一般的最小相位系统可满足假设1) 。
由假设可知, ∂q∂η(0,0,0)是Hurwitz矩阵, 所以存在一个正常数k0和正定矩阵P2满足
vTP2{∂q∂η(0‚0‚0)}v=−k0∥v∥2。 (5)
由于∂q∂η(ξ‚η‚YΓ)的连续性, 存在 (0, 0) 的一个领域, 满足
vTP2{∂q∂η(ξ‚η‚YΓ)}v≤−k0∥v∥2。 (6)
假设2 a (ξ, …, η, YΓ) , b (ξ, η, YΓ) 满足
∥a(τ1‚υ1‚YΓ)+b(τ1‚υ1‚YΓ)u−a(τ2‚υ2‚YΓ)+b(τ2‚υ2‚YΓ)u∥≤l1∥τ1−τ2∥+l2∥υ1−υ2∥‚ (7)
其中, τ1, τ2∈Rr, υ1, υ2∈Rn-r, l1, l2为大于零的常数。
∥q(τ1‚η‚YΓ)−q(τ2‚η‚YΓ)∥≤l3∥τ1−τ2∥‚ (8)
其中, τ1, τ2∈Rr, η2∈Rn-r, l3为大于零的常数。只要式 (4) 的等号右边各项是全局Lipschitz的, 均可满足假设2、假设3。令P1满足等式:
AT1P1+P1A1=−Ir‚ (9)A1=⎡⎣⎢⎢⎢⎢−k1−k2⋮−kr10⋮001⋮0⋯⋯ ⋯00⋮0⎤⎦⎥⎥⎥⎥,
sr+k1sr-1+…+kr=0的根在左开半平面。
《3 观测器设计》
3 观测器设计
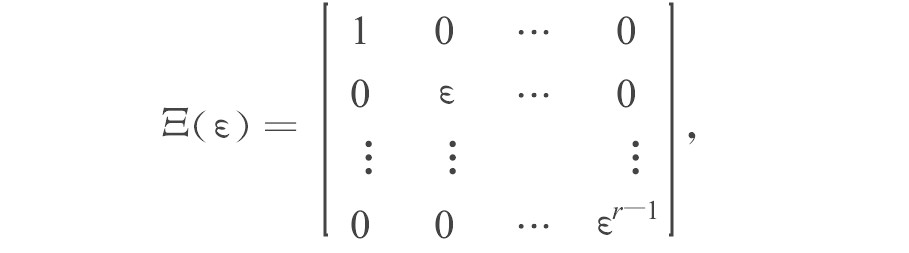
设P1 (ε) =Ξ (ε) T, P1Ξ (ε) , 所以,
令ζ1=Ξ (ε) z1。由‖Ξ (ε) -1‖=ε1-r得‖z1‖≤ε1-r‖ζ1‖=ε1-r。且由‖BTΞ (ε) ‖=εr-1得
V˙≤−12ε(1−2r)∥ζ1∥2+2ε(2−2r)(l2∥P1∥+l3∥P2∥)∥ζ1∥∥z2∥−k0∥z2∥2≤−34k0∥z2∥2−(12ε(1−2r)−4k0ε(2−2r)(l2∥P1∥+l3∥P2∥))∥ζ1∥2。
V˙≤−34k0∥z2∥2−14ε(1−2r)∥ζ1∥2,
《4 控制器设计》
4 控制器设计
σ˙(t)=−k1σ(t)−k2σ(t)q/p, (12)
其中, k1, k2>0, p, q均为大于零的奇数, 且p>q。解上述微分方程, 可得k1σ (t) (p-q) /p+k2=c exp (-[k1 (p-q) ]t/p) , 设x (0) ≠0, 可得c=k1σ (0) (p-q) /p+k2。所以, 当σ (ts) =0时, 可解出ts=[p/k1 (p-q) ]ln (k1σ (0) (p-q) /p+k2) /k2。可知变量σ在t≥ts时达到零并保持不变。
利用上述微分方程的解在有限时间内为零并保持不变的性质, 设计滑模变量为
σ(t)=(ddt+λε1)r−1e1=e(r−1)1+a1ε1e(r−2)1+⋯+ar−2εr−21e˙1+ar−1εr−11e1。 (13)
趋近律如式 (12) 所示。λ, ε1>0, ε1为摄动参数。其中, ∏i=1r−1(s+λi)=0与sr-1+a1sr-2+…+ar-2s+ar-1=0等价, 并且λ1, …, λr-1均为大于零的互不相同的实数。k1, k2>0, p>q>0, 并且 p, q为奇数。进一步规定 (p+q) /2同时也为奇数, 用于以后的稳定性分析中Lyapunov函数微分不等式的构造。
可以看出, 当t≥ts时, σ≡0, 基于式 (12) , 当t≥ts得到一个r-1阶常系数微分方程
e(r−1)1+a1ε1e(r−2)1+⋯+ar−2εr−21e˙1+ar−1εr−11e1=0。 (14)
e1(t)=∑i=1nhiexp(−λiε1t), (15)
其中, hi为不等于零的常数。可以看出, 当ε1>0充分小时,
《图13》
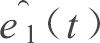
迅速向零收敛, 根据观测器的性质,
e1 (
t) 迅速向零收敛, 只需设计控制器使得变量到达滑模面式 (12) 即可。同时可以看到上述的
r-1阶常系数微分方程具有滤波作用, 并且由于
ε1>0的存在, 加快了
《图14》
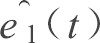
收敛速度。从而给出如下定理。
定理2 对于系统式 (4) , 采用式 (10) 所示的观测器, 控制器采用如下形式:
设Lyapunov函数为V=σ2 (t) /2, 所以,
V˙=σ(t)σ˙(t)=σ(t)(a(e,η,YΓ)+b(e,η,YΓ)u+v(t))=−k1σ2(t)−k2σ(t)(p+q)/p≤0。
《5 稳定性分析》
5 稳定性分析
当系统中有扰动、不确定项时, 非线性误差系统表示如下
⎧⎩⎨⎪⎪⎪⎪⎪⎪e∸=Ae¯+B[a(e¯,η)−y(r)Γ+ b(e¯,η)u+d(t)],η˙=q(e¯,⋯,η)。 (18)
其中 |d (t) |≤L1, L1为大于零的常数。
引理1[14] 如果W (X, t) 在开集D∈R2上是连续的, 且对微分方程
X˙(t)=W(X(t),t),X(t0)=X0 (19)
存在唯一解。如果X (t) 是上述微分方程在时域[t0, t1) 上的解, V (t) 是微分不等式
在时域[t0, t1]上的解, 且初始条件满足V (t0) ≤X (t0) , 则在时域[t0, t1]上存在不等式关系
定理3 对于系统式 (18) , 采用观测器式 (10) 、控制器式 (16) , 那么,
|e(i)1|≤2iϕε(r−i−1)1/λ(r−i−1)‚i=0,⋯,r−1‚ (22)
证明 选取Lyapunov函数为V=σ2 (t) /2, 沿着式 (18) 的解曲线求导, 得
V˙(t)=σσ˙=σ(a(e¯,η,YΓ)+b(e¯,η,YΓ)u+v(t)+d(t))=−θk1σ2−θk2σ(p+q)/p+σΘ(t)=−(θk1−Θ(t)/σ)σ2−θk2σ(p+q)/p<−(k1/γ−L/|σ|)σ2−1γk2σ(p+q)/p。 (25)
如果|σ|>γL/k1, 那么。V˙(t)=σσ˙<0。由式 (25) 得
V˙(t)≤−2(k1/γ−L/|σ|)V(t)−2(p+q)/2pk2V(t)(p+q)2/p/γ=−2μ1V(t)−2(p+q)/2pk2V(t)p+q)2/p/γ。 (26)
而由式 (12) 的分析, 且 (p+q) /2也为奇数, 所以微分方程
X˙(t)=−2μ1X(t)−2(p+q)/2pk2X(t)(p+q)/2/p/γ (27)
的解在有限时间内为零。当X (t0) =V (t0) >0时, 由引理1得0<V (t) ≤X (t) 。所以在有限时间内V (t) 到达零并保持不变。可以看出σ在有限时间后t1-t0, 保持在区域 {σ||σ|≤γL/k1} 内。或者式 (26) 可以写成
V˙(t)=−θk1σ2−(θk2−Θ(t)/σq/p)σ(p+q)/p≤−k1σ2/γ−(k2/γ−L/|σ|q/p)σ(p+q)/p。 (28)
如果|σ|> (γL/k2) p/q, 那么V˙(t)=σσ˙<0。由式 (28) , 得
V˙(t)≤−2k1V(t)/γ−2(p+q)/2p(k2/γ−L/|σ|q/p)V(t)(p+q)/2p=−2k1V(t)/γ−2(p+q)/2pμ2V(t)|p+q|/2p。 (29)
类似分析可知, 在有限时间内V (t) 到达零并保持不变。所以, 可以看出σ在有限时间后t2-t0保持在区域 {σ||σ|≤ (γL/k2) p/q} 内。
总之, σ有限时间段max (t1-t0, t2-t0) 后保持在区域
{σ||σ|≤ϕ=min{γL/k1,(γL/k2)p/q}}
|σ(t)|=∣∣e(r−1)1+a1ε1e(r−2)1+⋯+ar−2εr−21e˙1+ar−1εr−11e1∣∣≤ϕ。 (30)
所以, 可知ϕ/λn-1为有界层的宽度, 并且可得[14,15]
|e(i)1|≤(2λε1)iϕ/(λε1)r−1=2iεr+i−11ϕλr+i−1‚i=0,⋯,r−1。
《6 仿真》
6 仿真
x˙=⎡⎣⎢⎢⎢⎢x1x2−x31x1−x3x21+x2⎤⎦⎥⎥⎥⎥+⎡⎣⎢⎢⎢⎢02+2x300⎤⎦⎥⎥⎥⎥u+M(x)w‚y=h(x)=x4。
∂h/∂x=[0 0 0 1],Lgh(x)=0,Lfh(x)=x21+x2,LgLfh(x)=2(1+x3),L2fh(x)=2x21x2−2x41+x1。
可知系统的相对阶为2。令ξ1=h (x) =x4, ξ2=Lfh (x) =x2+x21, 得到η1=x3, η2=x1。因此, Jacobi矩阵
∂∂xχ(x)=⎡⎣⎢⎢⎢⎢02x101010000101000⎤⎦⎥⎥⎥⎥
是非奇异的, 并且逆变换为x1=η2, x2=ξ2-η22, x3=η1, x4=ξ1。
参考输入为yΓ=2e-05tsin 0.5t+cos t+d (t) , |d (t) |<0.1。
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪e˙1=e2,e˙2=η2+η2(η2(e2−η22)−η32)+ (2+2η1)u−y(2)d‚η˙1=−η1‚η˙2=−2η32+e2η2。
σ˙(t)=−k1σ(t)−k2σ(t)q/p,k1=2,k2=0.5,q=3,p=7。
《图23》

图1 系统输出误差曲线
Fig.1 The curve of output error for the system
《7 结论》
7 结论
由以上分析及仿真可知, 所设计的滑模控制器抗干扰性强, 且具有较快的收敛速度。
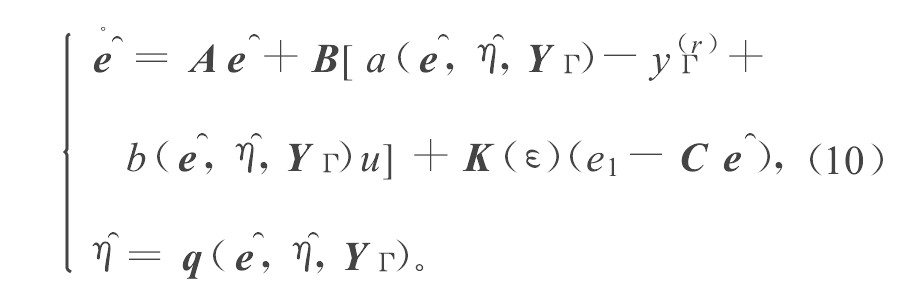
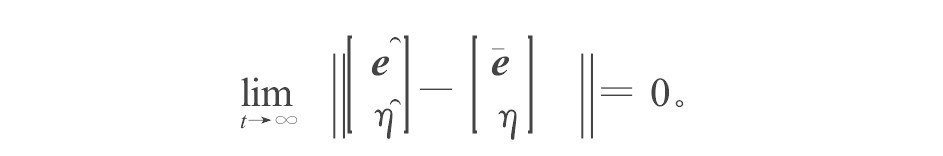

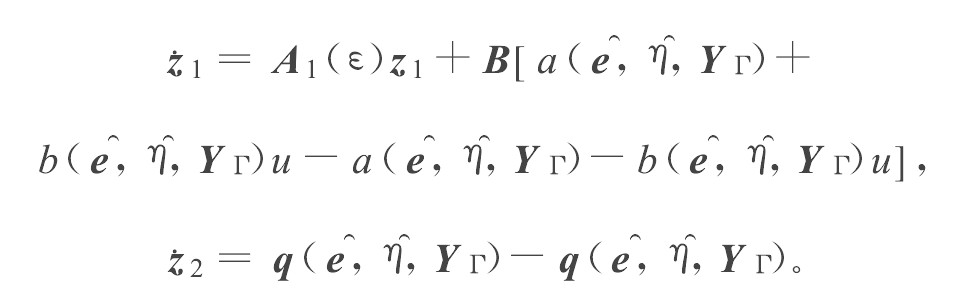

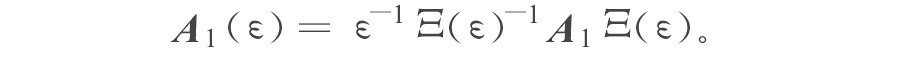
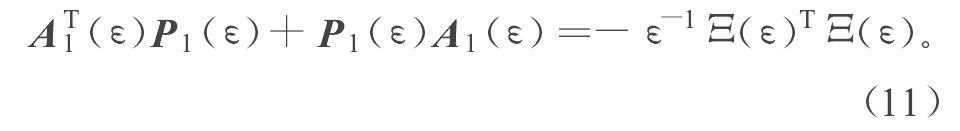


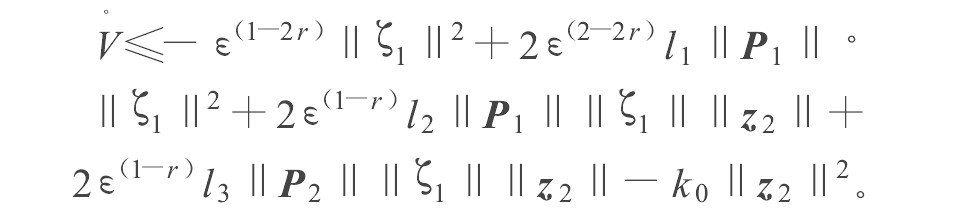
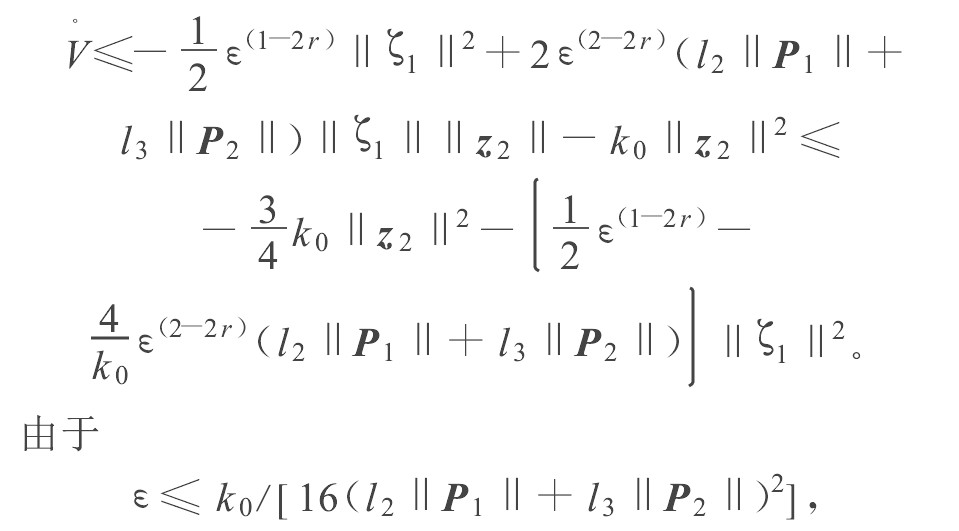
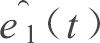
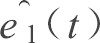
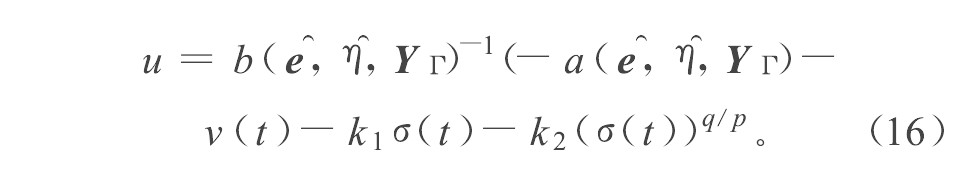
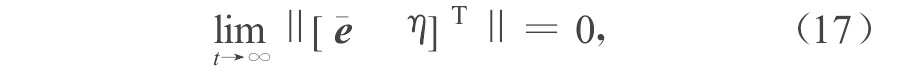
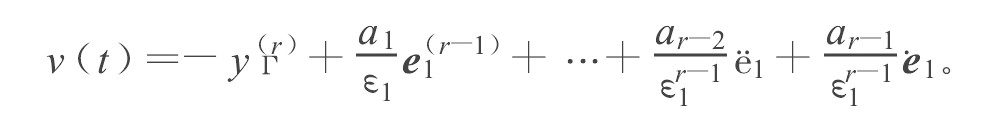
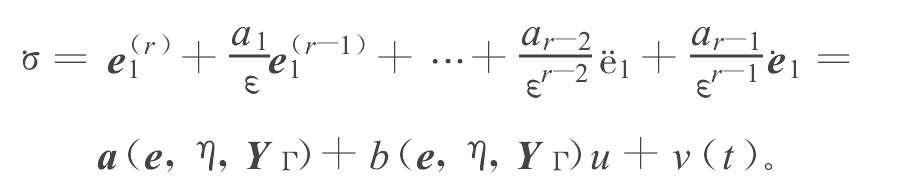
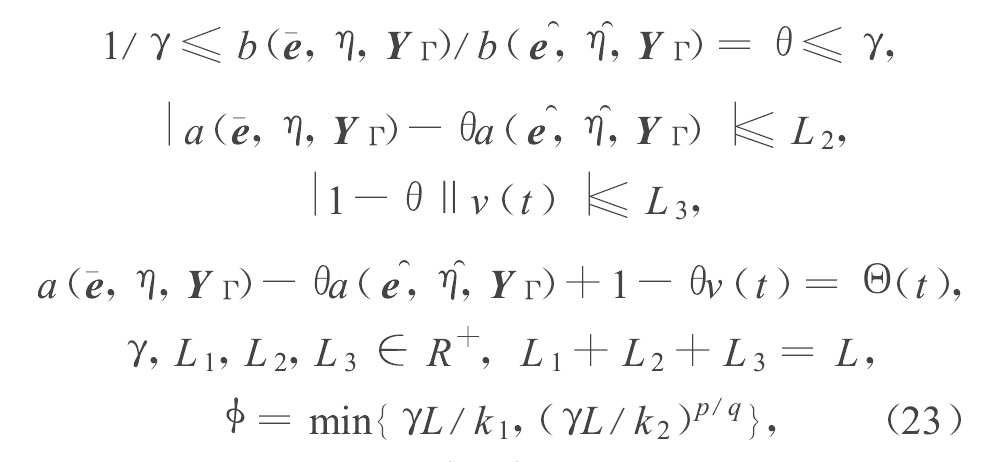
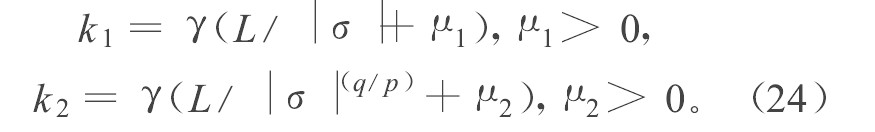

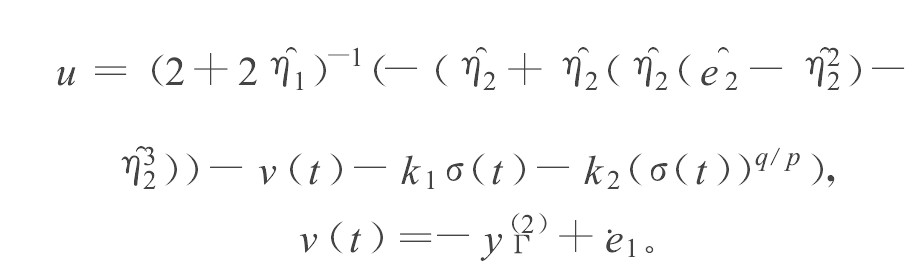














 京公网安备 11010502051620号
京公网安备 11010502051620号




