《1   前言》

1   前言

缓坡方程是研究波浪在近岸缓坡区域传播变形的一类有效波浪数学模型。双曲型缓坡方程综合考虑了波浪传播中的折射、绕射、反射等效应，且相对椭圆型缓坡方程在数值求解方面更为经济、高效，因而被广泛用于近岸波浪传播变形的理论研究和工程应用中。

Copeland[1] 在 Booj[2] 提出的随时间发展的椭圆型缓坡方程基础上，仿用 Ito 和 Tanimoto[3] 的算子分裂法推导出了经典的双曲型缓坡方程。随后 Madsen 和 Larsen[4] 在 Copeland[1] 提出的双曲型缓坡方程基础上消除时间快速因子，提出了随时间缓变型的双曲型缓坡方程，并结合内部造波法对其进行数值求解，提高了双曲型缓坡方程的数值求解效率。笔者采用时间层同步空间层交错的有限差分离散格式对 Madsen 和 Larsen 的双曲型缓坡方程进行数值离散求解，并结合 2 个典型算例对所提出的数值模型进行验证。

《2   数值模型》

2   数值模型

《2.1 双曲型缓坡方程》

2.1 双曲型缓坡方程

Copeland[1] 提出的双曲型缓坡方程形式如下：

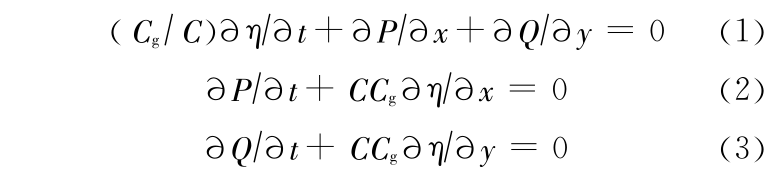
式中， C = ω/ k ，为波浪传播相速度，ω 为波浪角频率， k 为波数； Cg ＝，为波浪传播群速度；（ x，y，t）为瞬时波面升高； P 和 Q 为波浪水质点沿水深垂向积分的速度函数，常水深时分别表示为 P ＝， Q ＝，为波向角。

Madsen 和 Larsen[4] ，在 Copeland[1] 提出的双曲型缓坡方程基础上，消去了待求变量中快速变化的时间因子，提出了随时间缓慢发展的双曲型缓坡方程。如果考虑内部造波的影响，则该方程形式为

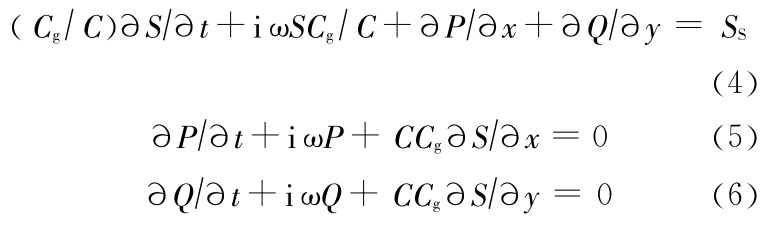
式中， i 为虚数单位； S，P，Q 分别为式（1）、式（2）和式（3）中的待求变量，P ，Q 消去快速变化的时间因子 后的相应变量形式； SS 为内部造波源项，如果造波源平行于 y 方向均匀布置，则可表示为 SS = 2 S0（Cg/Δx）cos ，S0 为入射波波面升高， 为波浪入射角。

《2.2 双曲型缓坡方程的数值离散》

2.2 双曲型缓坡方程的数值离散

Copeland[1] 采用空间和时间层同时交错的有限差分格式对式（1）、式（2）和式（3）进行了数值离散求解，郑永红[5] 采用时间层同步空间层交错的有限差分格式对式（1）、式（2）和式（3）进行了数值离散求解，并证明该格式的稳定性要优于 Copeland 采用的离散格式。

Madsen 和 Larsen[4] 采用空间层和时间层同时交错的数值离散格式对式（4）、式（5）和式（6））进行了数值求解。笔者结合文献[5]采用的时间层同步空间层交错的有限差分格式对式（4）、式（5）和式（6）进行数值离散求解。各差分变量的空间网格布置如图 1 所示，其中 P 定义在“→”处， Q 定义在“↑”处， S 和其他变量均定义在“O”处。

《图 1》

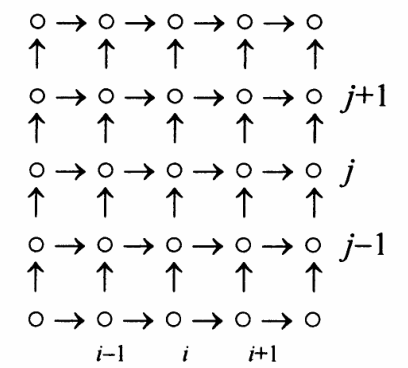
图 1 交错网格布置图

Fig.1 Disposition of variables in staggered grid

方程数值求解结合 ADI 有限差分格式进行，即前半时间步长在 x 方向采用隐式格式， y 方向采用显式格式；后半时间步长在 x 方向采用显式格式， y 方向采用隐式格式。

对式（4）、式（5）和式（6）的具体离散过程如下：

1）前半时间步长（t → t + Δt/2）

其中， E = Cg/C ，F ＝ CCg 。

对式（7）、式（8）和式（9）整理后得

其中

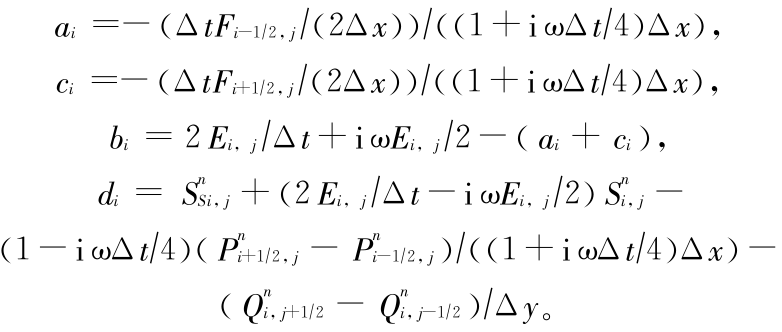
2）后半时间步长

对式（13）、式（14）和式（15）整理后得

其中

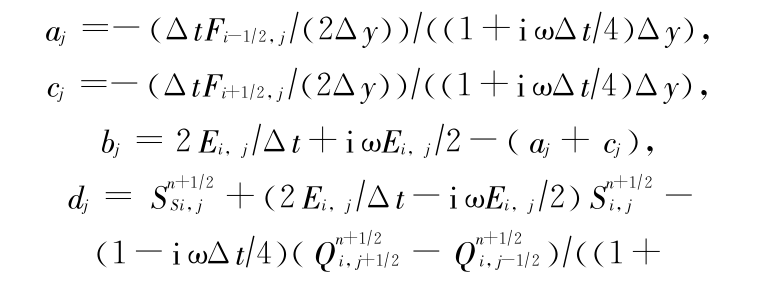
可以看出在上述前后各半个时间步长形成的离散方程中，变量 S 可分别形成三对角方程组，因此，可结合三对角追赶法对其进行快速求解，进而求解出相应的其他相关待求变量。

《2.3 边界条件》

2.3 边界条件

对于简谐波，如果不考虑入射边界处波浪反射作用的影响，则波浪入射边界条件为

式中为 t 时刻的波浪入射位置坐标； 为波浪入射处波向角；A0 为入射波振幅。

其他边界条件均可取为辐射边界条件，如采用内部造波法则在原入射边界处也取为辐射边界条件。所采用的辐射边界条件

与传统的双曲型方程辐射边界条件略有区别，其中 α≈ 0 ~ 1 ，为边界反射系数，当 α = 1 时，即为全辐射边界条件；α = 0 时，为全反射边界条件。在上述辐射边界条件中可看出，采用上述辐射边界条件时须首先确定边界处未知的波向角。对于复杂地形，由于波浪的反射、折射等效应，使得边界处的波向不易确定，借用边界阻尼层消波法[6] 将传至边界处的波能量吸收掉，可避免由于边界处波向不定带来的边界条件处理困难。但在应用边界阻尼层消波法时须注意，不合理的边界阻尼层摩阻系数会带来较大的边界反射问题。为了消除入射边界处的波浪反射效应，采用内部造波法并结合边界阻尼层消波法来处理入射边界处的波浪反射问题。

《3   数值模型的验证及计算结果分析》

3   数值模型的验证及计算结果分析

《3.1 Berkhoff 的椭圆形浅滩模型验证》

3.1 Berkhoff 的椭圆形浅滩模型验证

Berkhoff[7] 的椭圆形浅滩模型实验被广泛用来验证波浪传播数学模型的合理性。实验地形的平面布置如图 2 所示。

《图 2》

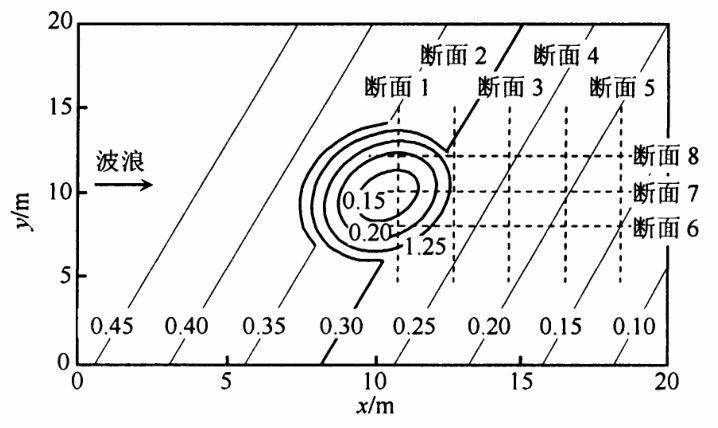
图 2 Berkhoff 椭圆形浅滩地形及实测断面布置图

Fig.2 Topography set and measured section of Berkhoff’s elliptical shoal case

计算中计算区域取为 21.5 m × 20.0 m ，斜坡旋转后的坐标（x′，y′）与计算坐标（x ，y）之间的转换关系为

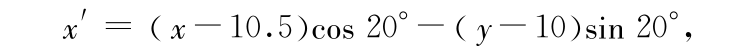
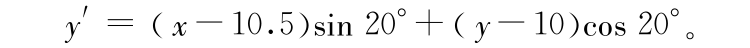
椭圆形浅滩中心对应于坐标（x′，y′）＝（0，0），其边界定义为

平底区域及斜坡上水深为

椭圆形浅滩上水深为

实验中波高为0.023 2 m ，周期为 1.0 s 的入射波浪沿 x 方向传入计算区域。数值计算时，将整个计算区域划分为 215 × 200 个计算网格，即 x，y 向的空间步长均为 0.1 m 。对 Copeland 双曲型缓坡方程和 Madsen 和 Larsen 双曲型缓坡方程的计算过程进行了比较。采用 Copeland 双曲型缓坡方程数值计算时，时间步长取为 0.1 s ，共计算 200 个时间步可达到稳定；采用 Madsen 和 Larsen 双曲型缓坡方程数值计算时，时间步长可取为 0.25 s ，共计算 100 个时间步即可达到稳定。相比较之下， Madsen 和 Larsen 双曲型缓坡方程的计算效率要比 Copeland 双曲型缓坡方程的计算效率高得多。图 3 给出了该地形下 8 个断面的数值模拟值和实测值的比较，可以看出各断面的计算值和实测值均符合得比较良好。

《图 3》

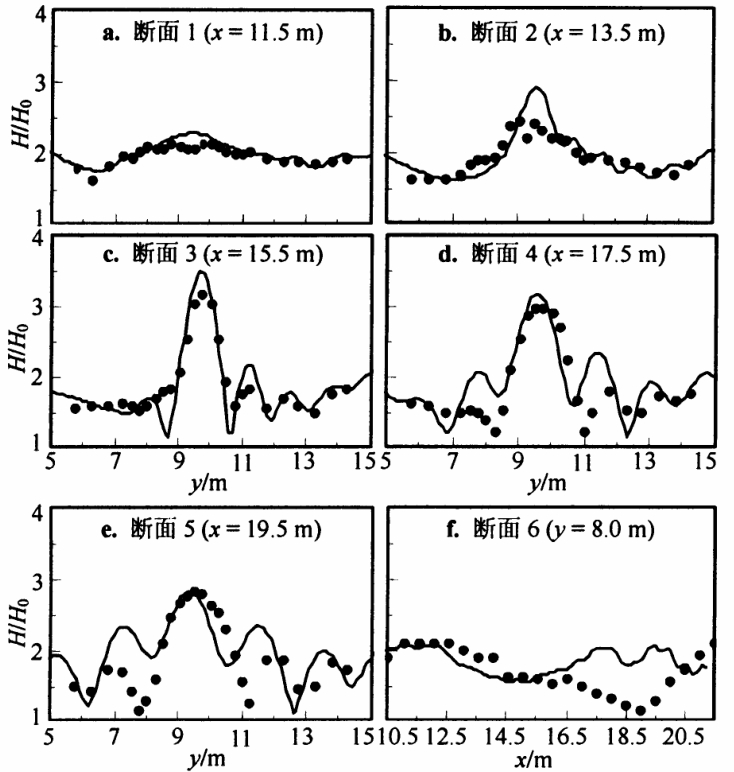
图 3 Berkhoff 椭圆形浅滩地形波高的数值解和实测值比较

Fig.3 Comparison between calculated and measured wave height for Berkhoff’s elliptical shoal case

《3.2 双突堤模型实验验证》

3.2 双突堤模型实验验证

大连理工大学海岸和近海工程国家重点实验室进行了波浪在双突堤后缓坡地形传播的实验[8] 。实验地形平面布置如图 4 所示。双突堤后为1∶50的斜坡，堤后水深为

《图 4》

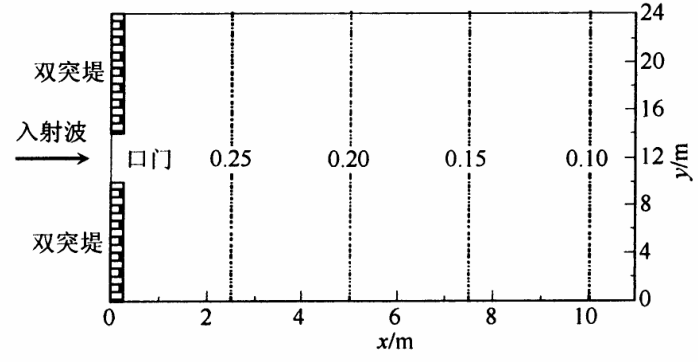
图 4 双突堤地形平面布置图

Fig.4 Topography set of the single gate breakwater case

实验中双突堤口门宽度分别设置为 2.0 m 和4.0 m ，以堤后 11.0 m × 24.0 m 为计算区域。数值计算中，将整个计算区域划分为 110 × 240 个等间距计算网格。实验中波高为 0.06 m ，周期为 1.41 s 的入射波浪沿 x 方向传入计算区域。

图 5 分别给出了口门宽度为 2.0 m 和 4.0 m时，数值模拟所得双突堤后的相对波高分布等值线图和实测相对波高分布等值线图。由图 5 可看出，在双突堤后存在较小的波高聚集区，且计算所得波高分布趋势和实测结果符合的相对一致，从而也验证了所采用的数值计算模型的有效性。

《图 5》

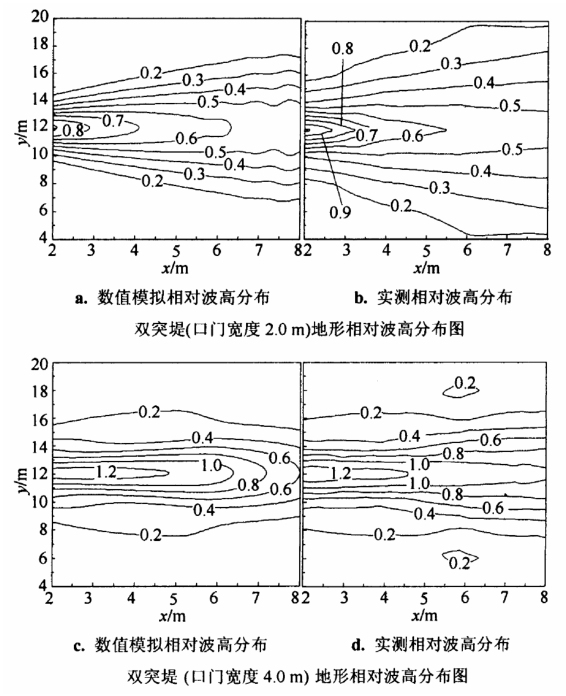
图 5 双突堤地形相对波高数值模拟值和实测值比较

Fig.5 Comparison between calculated and measured wave height for the single gate breakwater case

《4   结论》

4   结论

双曲型缓坡方程综合考虑了波浪传播过程中的折射、绕射、反射等效应，且数值求解过程相对于椭圆型缓坡方程更为经济、高效，在理论研究和工程应用领域受到愈来愈多的关注。用一种时间层同步空间层交错的数值离散格式对 Madsen 和 Larsen[4] 的双曲型缓坡方程进行了数值求解，并结合典型算例对所采用的数值模型进行了验证。数值计算结果表明，该数值模型可有效地应用于双曲型缓坡方程的数值求解。