选择逻辑函数的密码学性质

摘要

通过计算选择逻辑函数的Walsh循环谱和自相关函数，系统分析了选择逻辑函数的密码学性质。所得结论表明选择逻辑函数在变元个数较大的情况下具有理想的稳定性，能够抵抗最佳仿射（BAA）攻击，但是其“扩散”特性不够理想，在一定意义下不能有效地抗击差分攻击。讨论了与选择逻辑函数线性等价意义下满足严格雪崩准则或具有相关免疫性的逻辑函数构造问题。

正文

《1 引言》

1 引言

逻辑函数在当今密码设计与分析中的重要性是众所周知的, 因而20多年来关于逻辑函数的性质及具有特殊性质的逻辑函数的构造一直是密码学中最活跃的研究领域之一。文献[1]介绍了推广的Geffe发生器 (见图1) , 它是由2ⁿ+1个线性移位寄存器 (LFSR) 和一个选择逻辑函数组成, 其中LFSR-2ⁿ+1比其他2ⁿ个LFSR运行快n倍。当n=1时, 此发生器就是Geffe发生器^[2], 不能抵抗相关攻击^[3]。目前有关推广的Geffe发生器的复合器中使用选择逻辑函数的研究成果还不多见。

《图1》

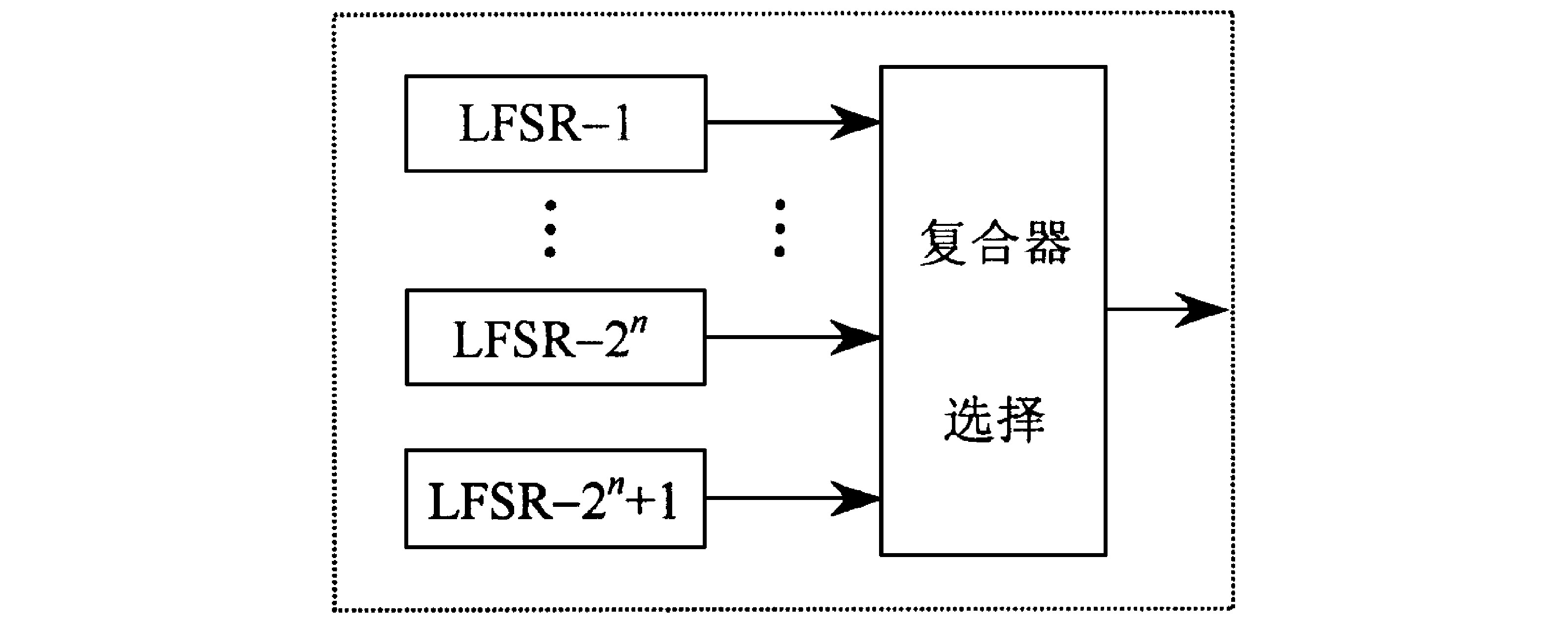
图1 推广的Geffe发生器

Fig.1 Generalized Geffe generators

笔者分析了推广的Geffe发生器的复合器中使用的选择逻辑函数的Walsh循环谱和自相关函数, 得到如下结论: n+2ⁿ元选择逻辑函数f (x, y) 的Walsh循环谱的取值为0或±2^-n, 因而对于较小的n, 抵抗相关攻击的能力比较弱;对于较大的n, f (x, y) 的稳定性比较理想, 能够抵抗最佳仿射 (BAA) 攻击;尽管f (x, y) 只有一个非零线性结构点, 但是对于较大的n其自相关函数值接近于1或-1的点很多, 特别有大部分汉明重量为1, 2等的点的自相关函数值接近于1和大部分汉明重量为2ⁿ-1, 2ⁿ-2等的点的自相关函数值接近于-1, 因而f (x, y) 在一定意义下不能有效地抗击差分攻击。

为了进一步提高f (x, y) 抵抗密码分析的能力, 讨论了与f (x, y) 线性等价意义下或满足严格雪崩准则^[4]、或具有相关免疫^[5] 性、或同时具有这两种性质的逻辑函数构造问题。

《2 基本概念》

2 基本概念

《2.1汉明重量的定义》

2.1汉明重量的定义

设w= (w₁, w₂, …, w_n) ∈GFⁿ (2) 是n维布尔向量, 称w= (w₁, w₂, …, w_n) 的不为零的分量的个数为其汉明重量, 且记之为W_H (w) 。

《2.2点积的定义[6]》

2.2点积的定义[6]

设x= (x₁, x₂, …, x_n) ∈GFⁿ (2) , w= (w₁, w₂, …, w_n) ∈GFⁿ (2) , x和w的点积定义为

$w \cdot x = w_{1} x_{1} + w_{2} x_{2} + \dots + w_{n} x_{n} (m o d 2) 。$ $w \cdot x = w_{1} x_{1} + w_{2} x_{2} + \dots + w_{n} x_{n} (m o d 2) 。$

《2.3选择逻辑函数的定义》

2.3选择逻辑函数的定义

根据推广的Geffe发生器中LFSR-2ⁿ+1比其他2ⁿ个LFSR运行快n倍, 可以假定LFSR-2ⁿ+1输出x= (x₁, x₂, …, x_n) , LFSR-1输出y₁, LFSR-2输出y₂, …, LFSR-2ⁿ输出y_2ⁿ由于y₁, y₂, …, y_2ⁿ的取值互不相干, 就可以如下定义选择逻辑函数:

若n+2ⁿ元布尔函数为

$\begin{array}{l} f (x, y) = x_{1} x_{2} \dots x_{n} y_{2^{n}} + (1 + x_{1}) x_{2} \dots x_{n} y_{2^{n} - 1} + \\ x_{1} (1 + x_{2}) \dots x_{n} y_{2^{n} - 2} + \dots + \\ (1 + x_{1}) (1 + x_{2}) \dots (1 + x_{n}) y_{1}, \\ (x, y) = (x_{1}, x_{2}, \dots, x_{n}, \\ y_{1}, y_{2}, \dots, y_{2^{n}}) \in G F^{n + 2^{n}} (2) ‚ \end{array}$ $\begin{array}{l} f (x, y) = x_{1} x_{2} \dots x_{n} y_{2^{n}} + (1 + x_{1}) x_{2} \dots x_{n} y_{2^{n} - 1} + \\ x_{1} (1 + x_{2}) \dots x_{n} y_{2^{n} - 2} + \dots + \\ (1 + x_{1}) (1 + x_{2}) \dots (1 + x_{n}) y_{1}, \\ (x, y) = (x_{1}, x_{2}, \dots, x_{n}, \\ y_{1}, y_{2}, \dots, y_{2^{n}}) \in G F^{n + 2^{n}} (2) ‚ \end{array}$

则称f (x, y) ) 为选择逻辑函数。

由定义可知:当x= (0, 0, …, 0) 时, f (x, y) =y₁;当x= (1, 0, …, 0) 时, f (x, y) =y₂;……;当x= (1, 1, …, 1) 时, f (x, y) =y_2ⁿ。

《2.4Walsh循环谱的定义[6]》

2.4Walsh循环谱的定义[6]

n元布尔函数f (x) , x∈GFⁿ (2) 的第二种Walsh变换定义为

$S_{(f)} (w) = 2^{- n} \sum_{x \in G F^{n} (2)} (- 1)^{f (x) + w \ 5 x}, w \in G F^{n} (2) ‚$ $S_{(f)} (w) = 2^{- n} \sum_{x \in G F^{n} (2)} (- 1)^{f (x) + w \ 5 x}, w \in G F^{n} (2) ‚$

称S_(f) (w) , w∈GFⁿ (2) 为f (x) 的Walsh循环谱。

《2.5自相关函数定义[7]》

2.5自相关函数定义[7]

设f (x) , x∈GFⁿ (2) 是布尔函数, 对

$\begin{array}{l} x = (x_{1}, x_{2}, \dots, x_{n}) \in G F^{n} (2), \\ s = (s_{1}, s_{2}, \dots, s_{n}) \in G F^{n} (2), \\ x + s = (x_{1} + s_{1}, x_{2} + s_{2}, \dots, x_{n} + s_{n}), \end{array}$ $\begin{array}{l} x = (x_{1}, x_{2}, \dots, x_{n}) \in G F^{n} (2), \\ s = (s_{1}, s_{2}, \dots, s_{n}) \in G F^{n} (2), \\ x + s = (x_{1} + s_{1}, x_{2} + s_{2}, \dots, x_{n} + s_{n}), \end{array}$

称

$r_{f} (s) = 2^{- n} \sum_{x \in G F^{n} (2)} (- 1)^{f (x) + f (x + s)}, s \in G F^{n} (2)$ $r_{f} (s) = 2^{- n} \sum_{x \in G F^{n} (2)} (- 1)^{f (x) + f (x + s)}, s \in G F^{n} (2)$

为f (x) 的自相关函数。

《3 主要结果》

3 主要结果

以下假定

$\begin{array}{l} X = (X_{1}, X_{2}, \dots, X_{n}), \\ Y = (Y_{1}, Y_{2}, \dots, Y_{2^{n}}), \\ (X, Y) = (X_{1}, X_{2}, \dots, X_{n}, Y_{1}, Y_{2}, \dots, Y_{2^{n}}) \end{array}$ $\begin{array}{l} X = (X_{1}, X_{2}, \dots, X_{n}), \\ Y = (Y_{1}, Y_{2}, \dots, Y_{2^{n}}), \\ (X, Y) = (X_{1}, X_{2}, \dots, X_{n}, Y_{1}, Y_{2}, \dots, Y_{2^{n}}) \end{array}$

中的X₁, X₂, …, X_n , Y₁, Y₂, …, Y_2ⁿ是定义在同一概率空间相互独立, 且具有均匀分布

$\begin{array}{l} Ρ {X_{i} = 0} = Ρ {X_{i} = 1} = \\ Ρ {Y_{j} = 0} = Ρ {Y_{j} = 1} = 2^{- 1}, \\ 1 \leq i \leq n ‚ 1 \leq j \leq 2^{n} \end{array}$ $\begin{array}{l} Ρ {X_{i} = 0} = Ρ {X_{i} = 1} = \\ Ρ {Y_{j} = 0} = Ρ {Y_{j} = 1} = 2^{- 1}, \\ 1 \leq i \leq n ‚ 1 \leq j \leq 2^{n} \end{array}$

的布尔随机变量^[7]。

选择逻辑函数f (x, y) 可以写成如下形式

$\begin{array}{l} f (x, y) = \\ \sum_{(a_{1}, \dots, a_{n}) \in G F^{n} (2)} (x_{1} + 1 + a_{1}) \dots (x_{n} + 1 + a_{n}) y_{\bar{a} + 1}, \\ (x, y) = (x_{1}, x_{2}, \dots, x_{n}, \\ y_{1}, y_{2}, \dots, y_{2^{n}}) \in G F^{n + 2^{n}} (2) ‚ \end{array}$ $\begin{array}{l} f (x, y) = \\ \sum_{(a_{1}, \dots, a_{n}) \in G F^{n} (2)} (x_{1} + 1 + a_{1}) \dots (x_{n} + 1 + a_{n}) y_{\bar{a} + 1}, \\ (x, y) = (x_{1}, x_{2}, \dots, x_{n}, \\ y_{1}, y_{2}, \dots, y_{2^{n}}) \in G F^{n + 2^{n}} (2) ‚ \end{array}$

其中非负整数 $\bar{a}$ $\bar{a}$ 的二进制展式为

$a_{n} + 2 a_{n - 1} + \dots + 2^{n - 2} a_{2} + 2^{n - 1} a_{1} 。$ $a_{n} + 2 a_{n - 1} + \dots + 2^{n - 2} a_{2} + 2^{n - 1} a_{1} 。$

根据

$\begin{array}{l} Ρ {f (X, Y) = 0} = \\ \sum_{a \in G F^{n} (2)} Ρ {f (X, Y) = 0, X = a} = \\ \sum_{a \in G F^{n} (2)} Ρ {Y_{\bar{a} + 1} = 0} Ρ {X = a} = \\ 2^{- 1} \sum_{a \in G F^{n} (2)} Ρ {X = a} = 2^{- 1} ‚ \end{array}$ $\begin{array}{l} Ρ {f (X, Y) = 0} = \\ \sum_{a \in G F^{n} (2)} Ρ {f (X, Y) = 0, X = a} = \\ \sum_{a \in G F^{n} (2)} Ρ {Y_{\bar{a} + 1} = 0} Ρ {X = a} = \\ 2^{- 1} \sum_{a \in G F^{n} (2)} Ρ {X = a} = 2^{- 1} ‚ \end{array}$

即知f (x, y) 是平衡的。

《3.1选择逻辑函数Walsh循环谱》

3.1选择逻辑函数Walsh循环谱

布尔函数的稳定性是判断其密码学性质的一个重要指标, 而布尔函数的稳定性是通过其Walsh循环谱予以刻画的^[6], 因而分析了选择逻辑函数的Walsh循环谱。

定理1 若f (x, y) 是n+2ⁿ元选择逻辑函数, 对任意的w∈GFⁿ (2) , v∈GF^2ⁿ (2) :

1) 当W_H (v) =1时, |S_(f) (w, v) |=2^-n;

2) 当W_H (v) ≠1时, S_(f) (w, v) =0。

证明:

1) 当W_H (v) =1时, 设v的第 $\bar{b} + 1$ $\bar{b} + 1$ 个分量为1,

$\begin{array}{l} b = (b_{1}, \dots, b_{n}) \in G F^{n} (2) ‚ \\ \bar{b} = b_{n} + 2 b_{n - 1} + \dots + 2^{n - 2} b_{2} + 2^{n - 1} b_{1} ‚ \end{array}$ $\begin{array}{l} b = (b_{1}, \dots, b_{n}) \in G F^{n} (2) ‚ \\ \bar{b} = b_{n} + 2 b_{n - 1} + \dots + 2^{n - 2} b_{2} + 2^{n - 1} b_{1} ‚ \end{array}$

由逻辑函数的Walsh循环谱的概率表示式^[7]可知,

$\begin{array}{l} S_{(f)} (w, v) = 2 Ρ {f (X, Y) + \\ (w, v) \cdot (X, Y) = 0} - 1 (1) \end{array}$ $\begin{array}{l} S_{(f)} (w, v) = 2 Ρ {f (X, Y) + \\ (w, v) \cdot (X, Y) = 0} - 1 (1) \end{array}$

因为

$\begin{array}{l} Ρ {f (X, Y) + (w, v) \cdot (X, Y) = 0} = \\ Ρ {f (X, Y) + w \cdot X + Y_{\bar{b} + 1}} = 0} = \\ \sum_{a \in G F^{n} (2)} Ρ {f (X, Y) + w \cdot X + Y_{\bar{b} + 1} = 0, \\ X = a} = \\ \sum_{a \in G F^{n} (2), a \neq b} Ρ {f (X, Y) + w \cdot X + Y_{\bar{b} + 1} = 0, \\ X = a} + Ρ {w \cdot b = 0, X = b} (2) \end{array}$ $\begin{array}{l} Ρ {f (X, Y) + (w, v) \cdot (X, Y) = 0} = \\ Ρ {f (X, Y) + w \cdot X + Y_{\bar{b} + 1}} = 0} = \\ \sum_{a \in G F^{n} (2)} Ρ {f (X, Y) + w \cdot X + Y_{\bar{b} + 1} = 0, \\ X = a} = \\ \sum_{a \in G F^{n} (2), a \neq b} Ρ {f (X, Y) + w \cdot X + Y_{\bar{b} + 1} = 0, \\ X = a} + Ρ {w \cdot b = 0, X = b} (2) \end{array}$

根据随机变量X₁, X₂, …, X_n, Y₁, Y₂, …, Y_2ⁿ之间的相互独立性可知

$\begin{array}{l} \sum_{a \in G F^{n} (2), a \neq b} Ρ {f (X, Y) + w \cdot X + Y_{\bar{b} + 1} = 0, \\ X = a} = \\ 2^{- 1} \sum_{a \in G F^{n} (2), a \neq b} Ρ {X = a} = 2^{- n - 1} (2^{n} - 1) ‚ (3) \end{array}$ $\begin{array}{l} \sum_{a \in G F^{n} (2), a \neq b} Ρ {f (X, Y) + w \cdot X + Y_{\bar{b} + 1} = 0, \\ X = a} = \\ 2^{- 1} \sum_{a \in G F^{n} (2), a \neq b} Ρ {X = a} = 2^{- n - 1} (2^{n} - 1) ‚ (3) \end{array}$

由式 (1) 至式 (3) 即得:

当w·b=0时,

$S_{(f)} (w, v) = 2 [2^{- n} + 2^{- n - 1} (2^{n} - 1)] - 1 = 2^{- n} ；$ $S_{(f)} (w, v) = 2 [2^{- n} + 2^{- n - 1} (2^{n} - 1)] - 1 = 2^{- n} ；$

当w·b≠0时,

$S_{(f)} (w, v) = 2 \times 2^{- n - 1} (2^{n} - 1) - 1 = - 2^{- n} 。$ $S_{(f)} (w, v) = 2 \times 2^{- n - 1} (2^{n} - 1) - 1 = - 2^{- n} 。$

所以,

$| S_{(f)} (w, v) | = 2^{- n} 。$ $| S_{(f)} (w, v) | = 2^{- n} 。$

2) 因为

$\begin{array}{l} \sum_{w \in G F^{n}, v \in G F^{2^{n}} (2), W_{Η} (v) = 1} [S_{(f)} (w, v)]^{2} = \\ \sum_{w \in G F^{n}, v \in G F^{2^{n}} (2), W_{Η} (v) = 1} 2^{- 2 n} = 1, \end{array}$ $\begin{array}{l} \sum_{w \in G F^{n}, v \in G F^{2^{n}} (2), W_{Η} (v) = 1} [S_{(f)} (w, v)]^{2} = \\ \sum_{w \in G F^{n}, v \in G F^{2^{n}} (2), W_{Η} (v) = 1} 2^{- 2 n} = 1, \end{array}$

再由能量守恒定理^[6] (Parseval定理) 知, 任给w∈GFⁿ (2) , v∈GFⁿ (2) , 当W_H (v) ≠1时,

$S_{(f)} (w, v) = 0 。$ $S_{(f)} (w, v) = 0 。$

综上所述, n+2ⁿ元选择逻辑函数f (x, y) 的Walsh循环谱的取值为0或±2^-n。由于当W_H (v) =1时, |S_(f) (w, v) |=2^-n, 因而对于较小的n, 抵抗相关攻击的能力比较弱;对于较大的n, f (x, y) 的稳定性比较理想, 能够抵抗最佳仿射 (BAA) 攻击。

《3.2选择逻辑函数的自相关特征》

3.2选择逻辑函数的自相关特征

逻辑函数的自相关函数能刻画逻辑函数的扩散特征和线性结构特征, 在逻辑函数的性质研究中发挥了重要作用^[7]。

引理1^[8] 设f (x) , x∈GFⁿ (2) 是布尔函数, 其自相关函数和Walsh谱分别为r_f (s) , s∈GFⁿ (2) 和S_(f) (w) , w∈GFⁿ (2) , 则

$\sum_{w \in G F^{n} (2)} S_{(f)}^{2} (w) (- 1)^{w \ 5 s} = r_{f} (s) ‚ s \in G F^{n} (2) 。$ $\sum_{w \in G F^{n} (2)} S_{(f)}^{2} (w) (- 1)^{w \ 5 s} = r_{f} (s) ‚ s \in G F^{n} (2) 。$

定理2 若f (x, y) 是n+2ⁿ元选择逻辑函数, 对任意的s∈GFⁿ (2) , t∈GF^2ⁿ (2) :

1) 当s≠ (0, 0, …, 0) 时, r_f (s, t) =0;

2) 记0= (0, 0, …, 0) ∈GFⁿ (2) , 则

$r_{f} (0, t) = 1 - 2^{1 - n} W_{Η} (t) 。$ $r_{f} (0, t) = 1 - 2^{1 - n} W_{Η} (t) 。$

证明

1) 由引理1和定理1可知,

$\begin{array}{l} r_{f} (s, t) = \sum_{w \in G F^{n} (2), v \in G F^{2^{n}} (2)} S_{(f)}^{2} (w, v) (- 1)^{w \ 5 s + v \ 5 t} = \\ \sum_{w \in G F^{n} (2), v \in G F^{2^{n}} (2) ‚ W_{Η} (v) = 1} S_{(f)}^{2} (w, v) (- 1)^{w \ 5 s + v \ 5 t} = \\ 2^{- 2 n} \sum_{v \in G F^{2^{n}} (2), W_{Η} (v) = 1} (- 1)^{v \ 5 t} \sum_{w \in G F^{n} (2)} (- 1)^{w \ 5 s} (4) \end{array}$ $\begin{array}{l} r_{f} (s, t) = \sum_{w \in G F^{n} (2), v \in G F^{2^{n}} (2)} S_{(f)}^{2} (w, v) (- 1)^{w \ 5 s + v \ 5 t} = \\ \sum_{w \in G F^{n} (2), v \in G F^{2^{n}} (2) ‚ W_{Η} (v) = 1} S_{(f)}^{2} (w, v) (- 1)^{w \ 5 s + v \ 5 t} = \\ 2^{- 2 n} \sum_{v \in G F^{2^{n}} (2), W_{Η} (v) = 1} (- 1)^{v \ 5 t} \sum_{w \in G F^{n} (2)} (- 1)^{w \ 5 s} (4) \end{array}$

当s≠ (0, 0, …, 0) 时,

$\sum_{w \in G F^{n} (2)} (- 1)^{w \ 5 s} = 0,$ $\sum_{w \in G F^{n} (2)} (- 1)^{w \ 5 s} = 0,$

因而可得

$r_{f} (s, t) = 0 。$ $r_{f} (s, t) = 0 。$

2) 由式 (4) 可知,

$\begin{array}{l} r_{f} (0, t) = 2^{- n} \sum_{v \in G F^{2^{n}} (2), W_{Η} (v) = 1} (- 1)^{v \ 5 t} = \\ 2^{- n} (2^{n} - 2 W_{Η} (t)) = 1 - 2^{1 - n} W_{Η} (t) 。 \end{array}$ $\begin{array}{l} r_{f} (0, t) = 2^{- n} \sum_{v \in G F^{2^{n}} (2), W_{Η} (v) = 1} (- 1)^{v \ 5 t} = \\ 2^{- n} (2^{n} - 2 W_{Η} (t)) = 1 - 2^{1 - n} W_{Η} (t) 。 \end{array}$

由定理2可知, 只有当W_H (t) =2ⁿ即t= (1, 1, …, 1) 时, r_f (0, t) =-1, 因而f (x, y) 只有一个非零线性结构点。

对取定的任一正整数k, 当t∈GF^2ⁿ (2) 且W_H (t) =k时, 有

$r_{f} (0, t) = 1 - \frac{k}{2^{n - 1}} \to_{n \to \infty}^{} 1;$ $r_{f} (0, t) = 1 - \frac{k}{2^{n - 1}} \to_{n \to \infty}^{} 1;$

当t∈GF^2ⁿ (2) 且W_H (t) =2ⁿ-k时, 有

$r_{f} (0, t) = - 1 + \frac{k}{2^{n - 1}} \to_{n \to \infty}^{} - 1 ‚$ $r_{f} (0, t) = - 1 + \frac{k}{2^{n - 1}} \to_{n \to \infty}^{} - 1 ‚$

因而当n较大时, GF^n+2ⁿ (2) 中大部分汉明重量为1, 2等点的自相关函数接近于1, 且大部分汉明重量为2ⁿ-1, 2ⁿ-2等点的自相关函数接近于-1, 故选择逻辑函数抵抗差分密码分析的能力比较弱, 在一定意义下不能有效地抗击差分攻击。

《3.3线性等价意义下满足严格雪崩准则或具有相关免疫性的逻辑函数构造》

3.3线性等价意义下满足严格雪崩准则或具有相关免疫性的逻辑函数构造

令x∈GF^n+2ⁿ (2) , 对n+2ⁿ元选择逻辑函数f (x) , 记

$\begin{array}{l} S_{f 0} = {w : w \in G F^{n + 2^{n}} (2) ‚ S_{(f)} (w) = 0} ‚ \\ R_{f 0} = {s : s \in G F^{n + 2^{n}} (2) ‚ r_{f} (s) = 0} ‚ \end{array}$ $\begin{array}{l} S_{f 0} = {w : w \in G F^{n + 2^{n}} (2) ‚ S_{(f)} (w) = 0} ‚ \\ R_{f 0} = {s : s \in G F^{n + 2^{n}} (2) ‚ r_{f} (s) = 0} ‚ \end{array}$

由定理1和定理2中的结论可知, S_f0所含元素个数是|S_f0|=2ⁿ (2^2ⁿ-2ⁿ) , 而R_f0所含元素个数是|R_f0|=2^2ⁿ (2ⁿ-1) +C^{2^n-1}_2ⁿ (2^2ⁿ-2ⁿ) 。

设f (x) 是n+2ⁿ元选择逻辑函数, 定义n+2ⁿ元布尔函数

$g (x) = f (x A + a) + b \cdot x + c, x \in G F^{n + 2^{n}} (2) ‚$ $g (x) = f (x A + a) + b \cdot x + c, x \in G F^{n + 2^{n}} (2) ‚$

其中a, b∈GF^n+2ⁿ (2) , c∈GF (2) , A是 (n+2ⁿ) × (n+2ⁿ) 可逆矩阵, 因为^[9]

$\begin{array}{l} r_{g} (s) = (- 1)^{b \cdot s} r_{f} (s A) ‚ s \in G F^{n + 2^{n}} (2) ‚ \\ S_{(g)} (w) = (- 1)^{c + a A^{- 1} (w + b)^{Τ}} \cdot \\ S_{(f)} ((w + b) (A^{- 1})^{Τ}) ‚ w \in G F^{n + 2^{n}} (2) ‚ \end{array}$ $\begin{array}{l} r_{g} (s) = (- 1)^{b \cdot s} r_{f} (s A) ‚ s \in G F^{n + 2^{n}} (2) ‚ \\ S_{(g)} (w) = (- 1)^{c + a A^{- 1} (w + b)^{Τ}} \cdot \\ S_{(f)} ((w + b) (A^{- 1})^{Τ}) ‚ w \in G F^{n + 2^{n}} (2) ‚ \end{array}$

由文献[9]中的结论可知:

a. 若取A是R_f0中任意n+2ⁿ个线性无关的向量为行所构成的矩阵, 则对任意b ∈GF^n+2ⁿ (2) , g (x) 不仅保持了选择逻辑函数f (x) 的稳定性, 而且满足严格雪崩准则。

根据定理2可知R_f0中存在线性空间GF^n+2ⁿ (2) 中的多组基:任选GFⁿ (2) 的一组基

α₁, …, α_n, 再任选GF^2ⁿ (2) 的一组基β₁, …, β $_{2}^{n}$ $_{2}^{n}$ , 则 (α₁, 0) , …, (α_n, 0) , 0= (0, 0, …, 0) ∈GF^2ⁿ (2) 和 (γ₁, β₁) , …, (γ_2ⁿ, β_2ⁿ ) , 0≠γ_i∈GFⁿ (2) , 1≤i≤2ⁿ 都是f (x) 的扩散点, 且它们显然是GF^n+2ⁿ (2) 中的一组基, 这样可以得到GF^n+2ⁿ (2) 中的

$\begin{array}{l} (2^{n} - 2^{0}) (2^{n} - 2^{1}) \dots (2^{n} - 2^{n - 1}) \times \\ (2^{2^{n}} - 2^{0}) (2^{2^{n}} - 2^{1}) \dots (2^{2^{n}} - 2^{2^{n} - 1)} (2^{n} - 1)^{2^{n}} \end{array}$ $\begin{array}{l} (2^{n} - 2^{0}) (2^{n} - 2^{1}) \dots (2^{n} - 2^{n - 1}) \times \\ (2^{2^{n}} - 2^{0}) (2^{2^{n}} - 2^{1}) \dots (2^{2^{n}} - 2^{2^{n} - 1)} (2^{n} - 1)^{2^{n}} \end{array}$

组基 (有序) 。因而可以由f (x) 线性等价地变换出大量满足严格雪崩准则且具有相同稳定性的逻辑函数。

b. 若取B是R_f0中任意n+2ⁿ个线性无关的向量为行所构成的矩阵, 令B= (A^-1) ^T, 再取b= (0, 0, …, 0) ∈GF^n+2ⁿ (2) , 则由选择逻辑函数f (x) 线性等价地变换出的g (x) 是平衡的, 且至少是1阶相关免疫的。

由|S_f0|=2ⁿ (2^2ⁿ-2ⁿ) 至少可以得到

$\begin{array}{l} (2^{n + 2^{n}} - 2^{2 n} - 2^{0}) (2^{n + 2^{n}} - 2^{2 n} - 2^{1}) \dots \cdot \\ (2^{n + 2^{n}} - 2^{2 n} - 2^{n + 2^{n} - 1}) \end{array}$ $\begin{array}{l} (2^{n + 2^{n}} - 2^{2 n} - 2^{0}) (2^{n + 2^{n}} - 2^{2 n} - 2^{1}) \dots \cdot \\ (2^{n + 2^{n}} - 2^{2 n} - 2^{n + 2^{n} - 1}) \end{array}$

个矩阵B, 可以由f (x) 线性等价地变换出大量平衡且具有相关免疫性的逻辑函数。

c. 由选择逻辑函数f (x) 线性等价地变换出既满足严格雪崩准则, 又具有相关免疫性的逻辑函数。例如, 当n=2时, 可取

$\begin{array}{l} A = (\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 0 & 1 & 1 \end{matrix}) \Rightarrow \\ B = (A^{- 1})^{Τ} = (\begin{matrix} 1 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 1 & 1 & 1 \end{matrix}) 。 \end{array}$ $\begin{array}{l} A = (\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 0 & 1 & 1 \end{matrix}) \Rightarrow \\ B = (A^{- 1})^{Τ} = (\begin{matrix} 1 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 1 & 1 & 1 \end{matrix}) 。 \end{array}$

根据定理1和定理2可知, 矩阵A满足a节中的条件, B满足a节和b节中的条件, 这时取b= (0, 0, …, 0) ∈GF⁶ (2) , 如此得到的g (x) 既满足严格雪崩准则又具有相关免疫性的逻辑函数。事实上容易证明, 对选定的满足a节中条件的A, 若存在S_f0中n+2ⁿ个向量 (不一定线性无关) 为行所构成的矩阵, 记为C, 使得

$C A^{Τ} + E = (b, b, \dots, b)^{Τ} ‚$ $C A^{Τ} + E = (b, b, \dots, b)^{Τ} ‚$

其中E是单位阵, b∈GF^n+2ⁿ (2) , 则对任意的a∈GF^n+2ⁿ (2) 和C∈GF (2) , 所得的g (x) 既满足严格雪崩准则又具有相关免疫性的逻辑函数。前述n=2的例子正好是C= (A^-1) ^T的特殊情况。

《4 结语》

4 结语

通过全面分析选择逻辑函数的Walsh循环谱和自相关函数, 说明选择逻辑函数当变元个数n不大时, 其密码学性质不好, 在n较大的情况下能够抵抗最佳仿射 (BAA) 攻击, 但是在一定意义上不能有效地抗击差分攻击。这些结果无疑对密码设计者和攻击者均有参考价值。此外, 笔者充分利用概率论的思想和方法, 对得出主要结论起了很好的作用。

展示更多