基于空间收缩的并行演化算法

摘要

提出了一种基于空间收缩的求解MINLP问题的新算法。算法应用了快速有效的不完全演化搜索较优解的分布信息，通过分布信息定位最优解的可能分布，再由精英个体信息决定下次搜索空间。仿真结果表明该算法在搜索效率、应用范围、解的精确性和鲁棒性上都优于其他现存演化算法。

正文

《1 引言》

1 引言

演化算法 (EA, evolutionary algorithms) 是近年来兴起的一类基于生物界的自然选择和自然遗传机制的计算方法^[1,2,3], 如遗传算法 (GA, genetic algorithms) 、演化策略 (ES, evolution strategy) ^[4,5] 等方法, 它是一类内在并行 (inherent parallelism) 的优化方法。这类方法的主要优点在于其本质上的并行性、广泛的可应用性和算法的高度鲁棒性、简明性与全局优化性, 其特性决定了它特别适合于解大规模并行模型。比较优秀的演化计算方法有DE算法 (differential evolution) ^[6]、基于DE和HDE的MIHDE算法 (mixed integer hybrid differential evolution) ^[7]、Guo Tao 的GT算法^[8] 以及ACSSOS算法^[9] 等。

大多数的演化算法在求解MINLP问题时, 由于问题的规模过大和算法本身的缺陷, 导致算法收敛速度过慢, 或者得到的解不准确, 甚至是不可行解。在算法中引入空间划分或空间收缩的思想, 可以快速的缩小寻优空间, 极大的提高收敛速度。现在大多数的空间搜索算法, 都是通过空间的划分和淘汰实现搜索, 本质上也是一类分支定界算法。它首先将解空间划分为若干子空间, 然后在每个子空间内分别选取若干个测试点, 通过测试点的好坏来确定保留与淘汰的空间。在局域性不好的搜索空间中, 如果这种算法保留的空间和测试点数不足够大, 很难找到全局最优点。MIHDE算法已经成功解决了很多MINLP问题, 但对有些问题得到的解的质量不高。GT算法是一种快速有效的空间搜索算法, 但它没有考虑求解非线性混合整数规划问题。另外, ACSSOS也是一种快速的空间收缩的算法, 但它要求适应值函数的搜索空间具有连续性和凸性, 对于不满足这些条件的问题便无能为力。

笔者研究的一种空间收缩算法应用了快速有效的不完全演化搜索较优解的分布信息^[9], 通过分布信息定位最优解的可能分布, 逐步缩小求解空间。收缩空间时由于采用了由精英个体决定下次搜索空间的方法, 因此使算法比其他同类空间收缩算法 (如ACSSOS) 具有更高的搜索效率, 应用范围也更广, 可以求解搜索空间为连续或离散的MINLP问题。演化策略采用了μ+1选择策略。

《2 混合整数优化问题的表示》

2 混合整数优化问题的表示

为不失一般性, MINLP问题可描述为:

$\begin{array}{l} \min_{x, y} f (x, y) ‚ \\ s . t . h_{i} (x, y) = 0, i = 1, \dots, m_{i}, \\ g_{j} (x, y) \leq 0, j = 1, \dots, m_{j}, \\ x^{l} \leq x \leq x^{u}, \\ y^{l} \leq y \leq y^{u} 。 \end{array}$ $\begin{array}{l} \min_{x, y} f (x, y) ‚ \\ s . t . h_{i} (x, y) = 0, i = 1, \dots, m_{i}, \\ g_{j} (x, y) \leq 0, j = 1, \dots, m_{j}, \\ x^{l} \leq x \leq x^{u}, \\ y^{l} \leq y \leq y^{u} 。 \end{array}$

其中:x= (x₁, x₂, …, x_{n_r}) 表示n_r维实型变量;

x^l= (x^l₁, x^l₂, …, x^l_{n_r}) , x^u= (x^u₁, x^u₂, …, x^u_{n_r}) 分别表示决策变量x的下、上界;

y= (y₁, y₂, …, y_{n_i}) 表示n_i 维整型变量;

y^l= (y^l₁, y^l₂, …, y^l_{n_i}) , y^u= (y^u₁, y^u₂, …, y^u_{n_i}) 分别表示决策变量y的下、上界。

引入下列记号:

解空间 S = { (x, y) |x^l ≤ x ≤ x^u ,

y^l ≤ y ≤ y^u };

空间的边长 (ω_x, ω_y ) = (x^u - x^l, y^u - y^l ) ;

空间的维数 n = n_r + n_i;

空间的中心 C_x= (C_x₁, C_x₂, …, C_{x_{n_r}}) =

$(\frac{x_{1}^{l} + x_{1}^{u}}{2}, \frac{x_{2}^{l} + x_{2}^{u}}{2}, \dots, \frac{x_{n_{r}}^{l} + x_{n_{r}}^{u}}{2});$ $(\frac{x_{1}^{l} + x_{1}^{u}}{2}, \frac{x_{2}^{l} + x_{2}^{u}}{2}, \dots, \frac{x_{n_{r}}^{l} + x_{n_{r}}^{u}}{2});$

c_y= (C_y₁, C_y₂, …, C_{y_{n_r}}) =

$(\frac{y_{1}^{l} + y_{1}^{u}}{2}, \frac{y_{2}^{l} + y_{2}^{u}}{2}, \dots \frac{y_{n_{r}}^{l} + y_{n_{r}}^{u}}{2} 。)$ $(\frac{y_{1}^{l} + y_{1}^{u}}{2}, \frac{y_{2}^{l} + y_{2}^{u}}{2}, \dots \frac{y_{n_{r}}^{l} + y_{n_{r}}^{u}}{2} 。)$

点到中心距离 $R = \sqrt{R_{x}^{2} + R_{y}^{2}},$ $R = \sqrt{R_{x}^{2} + R_{y}^{2}},$

R $_{x}^{2}$ $_{x}^{2}$ = (x₁-C_x₁) ²+…+ (x_{n_r}-C_{x_{n_r}}) ²,

R $_{y}^{2}$ $_{y}^{2}$ = (y₁-C_y₁) ²+…+ (y_{n_i}-C_{y_{n_i}}) ²;

$\begin{array}{l} 空间的半径 R = \max (R_{l}, R_{u}), \\ R_{l} = \sqrt{(R_{x}^{l})^{2} + (R_{y}^{l})^{2}}, \\ R_{u} = \sqrt{(R_{x}^{u})^{2} + (R_{y}^{u})^{2}} 。 \end{array}$ $\begin{array}{l} 空间的半径 R = \max (R_{l}, R_{u}), \\ R_{l} = \sqrt{(R_{x}^{l})^{2} + (R_{y}^{l})^{2}}, \\ R_{u} = \sqrt{(R_{x}^{u})^{2} + (R_{y}^{u})^{2}} 。 \end{array}$

这里x表示n_r维实型变量 (x∈R^n_r) , y表示n_i维整型变量 (y∈I^n_i) , 上述问题的目标函数、等式约束、不等式约束都是非线性的, 称为带约束的非线性混合整数规划。求解这类问题的一般方法是通过惩罚函数将其变成无约束问题, 惩罚适应函数为

$\begin{array}{l} Φ (x, y) = f (x, y) + \sum_{k = 1}^{m_{i}} α_{k} h_{k}^{2} (x, y) + \\ \sum_{k = 1}^{m_{j}} β_{k} g_{k}^{2} (x, y), \end{array}$ $\begin{array}{l} Φ (x, y) = f (x, y) + \sum_{k = 1}^{m_{i}} α_{k} h_{k}^{2} (x, y) + \\ \sum_{k = 1}^{m_{j}} β_{k} g_{k}^{2} (x, y), \end{array}$

其中g_k (x, y) = max (0, g_k) 。

《3 算法的主要思想》

3 算法的主要思想

《3.1 不完全演化》

3.1 不完全演化

大多数的演化算法在运行初期, 群体中个体的适应值改进较快, 执行到一定代数后, 群体中的个体分散在各个峰值附近, 此后用遗传操作很难再改进后代适应值, 从而导致收敛速度变慢。如果当个体分散在各个峰值附近时停止演化, 便称之为不完全演化算法。它的优点是可以快速获取较优点信息。重复进行不完全演化, 便可获得足够多的较优点信息, 为定位最优解、缩小解空间提供依据。

《3.2μ+1选择策略》

3.2μ+1选择策略

μ+1是演化策略中一种有效的选择策略, 它利用群体中μ个个体的信息产生一个新个体, 若此新个体优于群体中的最差个体, 则将其取代。

《3.3 空间收缩的思想》

3.3 空间收缩的思想

通过在解空间内进行不完全演化, 快速获得足够数目的较优点信息。将传统的根据空间来决定测试点的方法, 改为由测试点来决定空间, 把保留空间改为保留测试点。测试点选取不完全演化后的精英解, 由精英解决定的空间作为下一代的解空间。这样做可以充分利用不完全演化得到的分布信息, 快速高效的对空间进行收缩。

《3.4 半限定数学方法》

3.4 半限定数学方法

若一个变量x_i的实际值是未知的, 但包含该变量实际值的一个取值区间是已知的, 那么这个变量就叫做半限定变量 (subdefinite variables) , 这个区间就是半限定变量真值的一个估计。半限定变量用符号X表示。当这个区间收缩为一个点时, 半限定变量转变为确定变量。为了衡量空间压缩的程度, 定义了限定度这个概念。

设有变量x = (x₁, x₂, …, x_n ) ∈Rⁿ, 其对应的半限定变量为X = (X₁, X₂, …, X_n ) , 则各半限定变量的限定度定义为

$γ (x_{i}) = \exp (- V_{i} / V^{'}_{i}), i = 1, 2, \dots, n 。$ $γ (x_{i}) = \exp (- V_{i} / V^{'}_{i}), i = 1, 2, \dots, n 。$

其中V_i表示收缩后变量x_i的取值范围, V′_i表示收缩前变量x_i的取值范围, 即

$\begin{array}{l} V_{i} = {\begin{matrix} | V_{i}^{\max} - V_{i}^{\min} |, & x_{i} 为连续变量 ‚ \\ Ν_{i}, & x_{i} 为离散变量； \end{matrix} \\ V^{'}_{i} = {\begin{matrix} | V^{'}_{i}^{\max} - V^{'}_{i}^{\min} |, & x_{i} 为连续变量 ‚ \\ Ν^{'}_{i}, & x_{i} 为离散变量。 \end{matrix} \end{array}$ $\begin{array}{l} V_{i} = {\begin{matrix} | V_{i}^{\max} - V_{i}^{\min} |, & x_{i} 为连续变量 ‚ \\ Ν_{i}, & x_{i} 为离散变量； \end{matrix} \\ V^{'}_{i} = {\begin{matrix} | V^{'}_{i}^{\max} - V^{'}_{i}^{\min} |, & x_{i} 为连续变量 ‚ \\ Ν^{'}_{i}, & x_{i} 为离散变量。 \end{matrix} \end{array}$

V $_{i}^{\max}$ $_{i}^{\max}$ 和V $_{i}^{\min}$ $_{i}^{\min}$ 为X_i 的区间端点, N_i为X_i的元素个数。

半限定变量的限定度越大, 原组合优化问题的解空间就被压缩的越大, 搜寻最优解所花的时间就会越短。

《3.5 空间收缩停止条件》

3.5 空间收缩停止条件

根据解空间的规模, 变量的限定度到达适当范围时停止收缩, 改为完全演化或其他快速算法。目前比较实用的算法如遗传算法、禁忌搜索、模拟退火等。

《3.6 遗传操作》

3.6 遗传操作

在不完全演化过程中, 遗传操作用来产生下一代的个体, 遗传操作中用到了交叉和变异算子。交叉操作要求交叉产生的子代能够比较均匀地分布在当前解空间内。群体中m个个体张成仿射空间 $S = {X | X = \sum_{i = 1}^{m} ω_{i} x_{i}}$ $S = {X | X = \sum_{i = 1}^{m} ω_{i} x_{i}}$ , 在满足 $\sum_{i = 1}^{m} ω_{i} = 1$ $\sum_{i = 1}^{m} ω_{i} = 1$ 的情况下, 适当地随机选取权值, 可使生成点比较均匀地分布在m个个体形成的最小凸集内。由m个父体产生一个个体 (x′, y′) 的交叉算子定义为:

$\begin{array}{l} x^{'} = \sum_{i = 1}^{m} α_{i} x_{i}, \\ y^{'} = e n t (\sum_{i = 1}^{m} α_{i} y_{i}) 。 \end{array}$ $\begin{array}{l} x^{'} = \sum_{i = 1}^{m} α_{i} x_{i}, \\ y^{'} = e n t (\sum_{i = 1}^{m} α_{i} y_{i}) 。 \end{array}$

随机产生α_i满足:

-0.5 ≤α_i ≤ 1.5, 且 $\sum_{i = 1}^{m} α_{i} = 1$ $\sum_{i = 1}^{m} α_{i} = 1$ 。

变异算子定义为:

$\begin{array}{l} x^{'} = x + τ Ν (0, σ^{'}), \\ y^{'} = y + τ Ν (0, σ^{'}), \\ σ^{'} = σ \exp [τ Ν (0, 1)] 。 \end{array}$ $\begin{array}{l} x^{'} = x + τ Ν (0, σ^{'}), \\ y^{'} = y + τ Ν (0, σ^{'}), \\ σ^{'} = σ \exp [τ Ν (0, 1)] 。 \end{array}$

式中, N (0, 1) 是均值为0、方差为1的正态分布随机变量, τ是算子集参数, 表示变异运算时的个体步长, σ用来调整个体进行变异操作时变异量的大小。遗传操作的具体方法是在种群中随机选取一个个体进行变异, 然后随机选取两个个体进行交叉, 将得到的新个体取代种群中的最差个体。

《3.7 算法流程》

3.7 算法流程

Step 1 在解空间内随机选取种群, 初始化优解池, 计算解空间参数。

Step 2 解空间内进行不完全演化r次, 更新优解池。

Step 3 选取适应值较好的个体和小概率的少量较差个体进入精英池。

Step 4 由精英池内个体确定下一代空间范围, 并计算其半径。若限定度满足要求范围, 转Step 5, 否则转Step 1。

Step 5 以收缩后的空间为解空间, 再应用完全演化算法求解。

《4 仿真》

4 仿真

为了检验算法的性能, 对下面两个优化问题进行了求解:

例1

$\begin{array}{l} \min_{x, y} f (x, y) = 0.6224 (0.0625 y_{1}) x_{1} x_{2} + \\ 1.7781 (0.0625 y_{2}) x_{1}^{2} + 3.1661 (0.0625 y_{1})^{2} x_{2} + \\ 19.84 (0.0625 y_{1})^{2} x_{1} \\ s . t . g_{1} (x, y) = 0.0193 x_{1} - 0.0625 y_{1} \leq 0, \\ g_{2} (x, y) = 0.00954 x_{1} - 0.0625 y_{2} \leq 0, \\ g_{3} (x, y) = 750 \times 1728 - π x_{1}^{2} x_{2} - 4 π x_{1}^{3} / 3 \leq 0, \\ g_{4} (x, y) = x_{2} - 240 \leq 0 。 \end{array}$ $\begin{array}{l} \min_{x, y} f (x, y) = 0.6224 (0.0625 y_{1}) x_{1} x_{2} + \\ 1.7781 (0.0625 y_{2}) x_{1}^{2} + 3.1661 (0.0625 y_{1})^{2} x_{2} + \\ 19.84 (0.0625 y_{1})^{2} x_{1} \\ s . t . g_{1} (x, y) = 0.0193 x_{1} - 0.0625 y_{1} \leq 0, \\ g_{2} (x, y) = 0.00954 x_{1} - 0.0625 y_{2} \leq 0, \\ g_{3} (x, y) = 750 \times 1728 - π x_{1}^{2} x_{2} - 4 π x_{1}^{3} / 3 \leq 0, \\ g_{4} (x, y) = x_{2} - 240 \leq 0 。 \end{array}$

这是一个压力容器设计问题, 由Sandgren^[10] 提供, 设计参数是容器的各种尺寸, 目标函数f (x, y) 是熔制压力容器的总成本, 约束条件保证容器符合美国机械工程师学会标准, 这是一个混合整数优化问题。下面是各种算法对上例的计算结果比较, 仿真程序参数表如表1和表2所示。

表1 例1各种算法计算结果比较

Table 1 Comparison among the results of various algorithms in example 1

《图1》

从表1和表2可以看出, 搜索空间收缩的幅度很大。限定度越大的变量, 其搜索空间的收缩幅度越大。求解例1的模型, 空间收缩算法耗时20 ms, 收敛速度大大快于其他几种算法。

表2 例1空间收缩算法仿真程序参数

Table 2 Parameters of simulated procedure in example 1

《表1》

	压缩前	压缩后	限定度
种群规模	100	100
空间半径	162.018 5	19.365 7
x₁范围	0～100	40.554 7～45.209 7	0.954 4
x₂范围	0～200	173.487 7～211.804 1	0.825 7
y₁范围	0～50	13～15	0.960 8
y₂范围	0～50	7～9	0.960 8

例2

$\min f (x) = \frac{\sin^{2} \sqrt{x_{1}^{2} + x_{2}^{2}} - 0.5}{[1 + 0.001 (x_{1}^{2} + x_{2}^{2})]^{2}}$ $\min f (x) = \frac{\sin^{2} \sqrt{x_{1}^{2} + x_{2}^{2}} - 0.5}{[1 + 0.001 (x_{1}^{2} + x_{2}^{2})]^{2}}$

这个实例来自Schaffer^[11], 已知上式的全局最优点是 (0, 0) , 目标函数f (x) 最优值为-0.5。函数的三维图如图1所示, 在距全局最优点附近有无限多个局部最优点。由于其强烈的振荡性以及全局最优点被局部最优点包围的特性, 一般优化算法很难找到它的全局最优值。

《图2》

图1 例2目标函数三维图

Fig.1 Three dimensional graph of the objective function in example 2

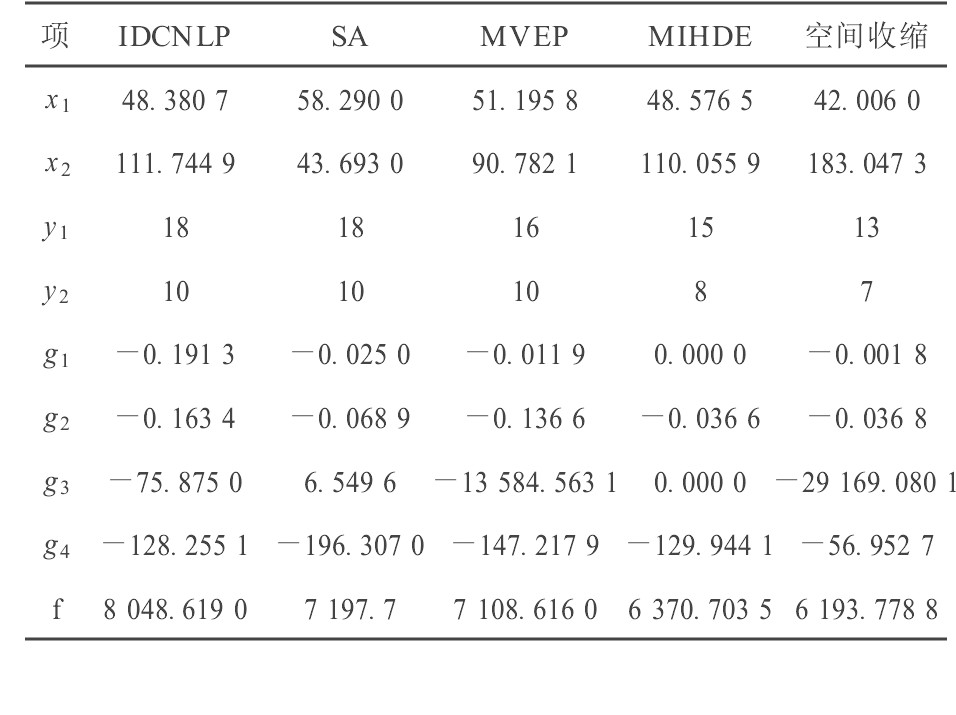
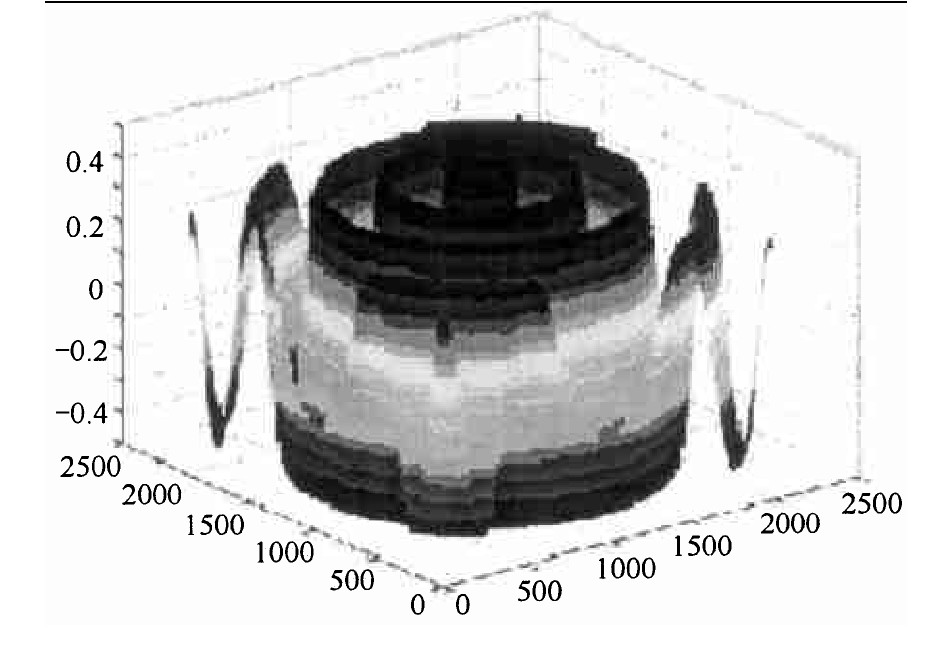
算法的运行结果如下:最佳个体为x₁= 0.001 377 55, x₂=-0.000 618 82;适应值为-0.499 997 71。仿真中各个参数如表3所示。

用空间收缩算法求解实例2的目标函数, 平均5次就有1次能找到全局最优解, 所用时间为10 ms, 即使在找不到最优解的情况里, 收缩后的空间也全都包含最优解。这说明空间收缩在定位最优解范围上还是非常快速和准确的, 之所以某些时候找不到全局最优解, 是因为空间收缩后的完全演化过程导致算法收敛到了局部最优点, 这时可以考虑增大空间收缩的限定度, 也就是使空间的收缩幅度更大。

表3 例2仿真程序参数

Table 3 Parameters of simulated procedure in example 2

《表2》

	压缩前	压缩后	限定度
种群规模	100	100
空间半径	14.142 1	3.620 3
x₁范围	-10～10	-2.889 6～3.166 7	0.738 7
x₂范围	-10～10	-1.367 3～2.60 2	0.820 0

另外, 笔者还用该算法求解了一个调度问题模型, 这是一个对多目标、多约束的MINLP模型进行求解的组合优化问题。该模型有100个决策变量, 120个约束方程, 算法完成空间收缩约用300～800 ms, 完成整个寻优过程约用600～1 100 ms, 而用普通遗传算法求解同样的模型并达到类似的结果大约用时15～25 s。

《5 结论》

5 结论

1) 根据上述仿真结果, 空间收缩能比较准确迅速地缩小解空间, 即使初始解空间很大, 算法也能在很短时间内完成。计算结果表明, 该算法在解的质量及收敛速度上优于一般的演化算法。

2) 在不完全演化中, 搜索空间越大, 函数的峰越多, 所需要的较优点信息也就越多, 需要进行不完全演化的次数也越多。所以在算法中可以考虑随着空间的收缩, 逐步减小不完全演化的次数, 从而进一步提高收缩速度。

3) 该算法采用了由精英个体决定下一代空间的方法, 在用精英解构造新空间后, 得到的是一个连续的凸空间, 与初始的解空间是否连续或是否凸无关。如果初始解空间是不连续或非凸, 新的解空间里可能包含不可行解, 由于采用了对不可行解加惩罚的方法, 选出的下一代精英解中将都是可行解, 经过几次收缩, 最终算法将空间收缩到一个连续的凸空间内。所以在解决搜索空间不连续的问题或空间非凸问题时, 可以把空间演化的过程看作为空间取舍和空间收缩同步进行的过程。

4) 在算法中, 主要的过程是解空间的不断演化, 而个体的选择与淘汰只是用来决定下一代的解空间, 上一代的超级个体并不带入下一代, 这样可以保证算法在运行之初不易陷入局部最优, 避免了早熟收敛。

展示更多