《1 引言》
1 引言
脉冲暂态混沌神经网络(PTCNN)将混沌动力用脉冲方式进行控制,施加于神经网络上,形成脉冲暂态混沌神经网络,使得混沌动力和神经收敛动力交替起作用,从而具有更强的跳出局部最小点的功能,可以更有效地进行问题的全局寻优[1~12]。PTCNN在解决无约束非线性规划问题时,利用其丰富的动力学性质,既可以不断地跟出极小点所在区域,又可以在极小点所在区域内稳定到极小点,从而尽量全面地找到包括全局和局部最小值[13]。对于有约束条件的非线性规划问题,只有将约束条件合理转换才能够充分利用PTCNN的良好性质来解决具有多个极小点的约束非线性规划问题。这里使用惩罚函数方法,对含有约丛条件的非线性规划问题进行处理[14],使得目标函数与约束条件合并成一个表达式,将其变成一个不含约束条件的非线性规划问题,进而用脉冲暂态混沌神经网络进行求解,得到了比较满意的结果。
《2 脉冲暂态混沌神经网络》
2 脉冲暂态混沌神经网络
本文应用以下脉冲暂态混沌神经网络模型:
\(\begin{array}{c} x_{i}(t)=\frac{1}{1+\exp \left(-y_{i}(t) \varepsilon_{i}\left(t_{l}\right)\right)} \\ y_{i}(t+1)=k_{i} y_{i}(t)+\alpha_{i}\left(\sum_{j=1}^{n} w_{i j} x_{j}(t)\right)- \\ z_{i}(t)\left(x_{i}(t)-I_{0}\right) \\ z_{i}\left(t_{l}\right)=\exp \left(-\frac{u(l)}{u_{1 i}}\right) \mu_{2 i i} \\ u(l)=-10+\frac{20}{m} z m(l-1) \\ \varepsilon_{i}\left(t_{l}\right)=\frac{1}{1+\left(\exp \left(-u(l) \times \lambda_{1 i}\right)\right) \lambda_{2 i}} \lambda^{j 3_{i}}, \\ i=1,2, \cdots, n \\ l=1,2, \cdots, \operatorname{round}\left(\frac{m}{z m}\right) \\ j j=1,2, \cdots, z m \end{array}\), (1)
其中\(w_{i j}=w_{j i}, w_{i i}=0\),\(\sum_{j=1, j \neq i}^{n} w_{i j} x_{j}-I_{i}=-\frac{\partial E}{\partial x_{i}}\);
E为能量函数,对应所求函数;xi为神经元i的输出;yi为神经元i的内部状态;wij表示从神经元i的连接权值;Ii为神经元i的偏置;I0为一正数,0≤I0≤1;a为一比例常数,0≤a≤1;k为神经隔膜的衰冶因子,0≤k≤1;zi(t)为自反馈连接权值或不应性强度,zi(t)≥0;l是相应于单个脉冲范围内的变量计数器;tl是相应于l的时间变量;u(l)是一个取值范临在[-10,10]之间的递增的数列,之所以取这个区间,是为了取得一个适合基本脉冲波形;m为迭代次数;zm为施加脉冲的次数;exp(-u(l))是一个基本脉冲函数;μ1i为控制脉沥波形的参数;μ2i是控制波形幅度的系数,对应于不同的函数而取不同的值;λ1,λ2为函数
\(\frac{1}{1+\left(\exp \left(-u(l) \times \lambda_{1}\right)\right) \lambda_{2}}\)的性态参数;λ3是εi的幅度函数,它控制着εi的变化区间。jj是与施加脉冲的次数zm相对应的序列,它的存在导致εi逐渐以低起点分段增加。
PTCNN包含许多可调参数,可以控制整个系统君现非常多样的动力特性,随着混沌脉冲的间欣加人使得系统可以不断地进人混沛和稳定状态,当极小点不止一个时,既可以不断地进人和跳出不同极小值的局域范围,又可以在局部区域内向此区域的极小值不断靠近,进而稳定到该极小值。使得系统可以更有效地进行问题的全局寻优。
《3 约束条件处理》
3 约束条件处理
约束条件的处理方法使用惩罚函数法进行,从而将约束非线性规划问题转变成只具有一个目标函数L(x)的无约束非线性规划问题。
设优化问题为
求xi
\(\begin{array}{c} \min \left(f\left(x_{i}\right)\right) \\ \text { s.t. } \quad g_{l}\left(x_{i}\right)<0 \\ i=1,2, \cdots, n \quad l=1,2, \cdots, N L \end{array}\)
其中n为变量个数;NL为约束条件个数;g(xi)为约束条件。构造罚函数L(xi);
\(L\left(x_{i}\right)=f\left(x_{i}\right)+\lambda \sum_{l=1}^{N L} \max \left(g_{l}\left(x_{i}\right), 0\right)\)
其中λ是罚因子,取一个大正数。则对于脉冲暂态混沌神经网络而言:
\(\sum_{j=1, j \neq i}^{n} w_{i j} x_{j}-I_{i}=-\frac{\partial L}{\partial x_{i}}\)
而
\(\begin{array}{c} \frac{\partial L\left(x_{i}\right)}{\partial x}=\frac{\partial f\left(x_{i}\right)}{\partial x_{i}}+ \\ \lambda \sum_{l=1}^{N L} \max \left(g_{l}\left(x_{i}\right), 0\right) \frac{\partial g_{l}\left(x_{i}\right)}{\partial x_{i}} \end{array}\)
所以 \(\begin{array}{l} \sum_{j=1, j \neq 1}^{n} w_{i j} x_{j}-I_{i}=-\left(\frac{\partial f\left(x_{i}\right)}{\partial x_{i}}+\right. \\ \left.\lambda \cdot \sum_{l=1}^{N L} \max \left(g_{l}\left(x_{i}\right), 0\right) \frac{\partial g_{l}\left(x_{i}\right)}{\partial x_{i}}\right) \end{array}\)
《4 算例》
4 算例
为说明PTCNN全局寻优的特点,首先给出一个无约束非线性规划算例1。
例1 求x
\(\text { s. t. } \quad \min \left(f=x^{2}(x-1)^{2}(x-5)^{2}-5\right)\)
参数取值。\(\begin{array}{l} {\left[k_{i}, \alpha_{i}, I_{0 i}, \mu_{1 i}, \mu_{2 i}, \lambda_{1 i}, \lambda_{2 i}, \lambda_{3 i}, m, n\right]=[1,1,} \\ 0.5,2,10,0.2,0.1,0.25,1000,1] 。 \end{array}\)。
结果如图1所示。
《图1》

图1 例1计算结果
Fig.1 Result of example 1
图1(a)为乙相图,图1(b)为f相图,庞线框中对应的是稳定设小点0,1,5,对应的极小值为0。全部为全局最小,全局最小值为-5。此例证明用脉冲暂态混沌神经网络可以拖到问题所有的全局极值点。
下面给出一个约束非线性规划的算例,同时作为比较,又计算了没有约束条件时的寻优结果,从对比可以发现罚函数法在PTCNN计算有约不问题时是有效的,系统对同一函数在条件不同时给出了不同结果。
例2:求x
\(\min \left(f=x^{2}(x-2)^{2}\right)\)
\(\text { s.t. } \quad \frac{1}{x}<1\)取得最小值。
首先将例2写成更一舱的优化问题形式,
求x
\(\begin{array}{c} \min \left(f=x^{2}(x-2)^{2}\right) \\ \text { s.t. } \quad g(x)=\frac{1}{x}-1<0 \end{array}\)
用罚函数法对问题进行变形,取2=100,则
\(\begin{array}{c} L(x)=x^{2}(x-2)^{2}+100 \max \left(\left(\frac{1}{x}-1\right), 0\right) \\ \frac{\partial L(x)}{\partial x}=x 2(x-2)^{2} \\ \quad+x_{2}(x-2) \cdot 2+ \\ \text { 所以 } 100 \max \left(\left(\frac{1}{x}-1\right), 0\right)\left(-\frac{1}{x^{2}}\right) \end{array}\)
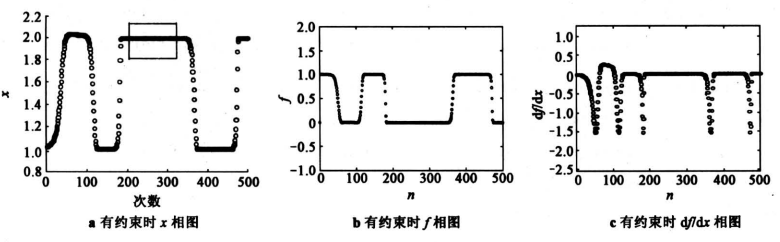
此外又取参数\(\left[k_{i}, \alpha_{i}, I_{0 i}, \mu_{1 i}, \mu_{2 i}, \lambda_{1 i}, \lambda_{2 i}\right. , \left.\lambda_{3 i}, m, n\right]=[1,1,0.5,2,100,0.2,0.1,0.28,500 , 1]\)。将参数输入PTCNN系统对罚函数进行寻优。图2是函数图形,图3是没加约束条件时得到的结果,寻找到两个最小点z=0,z=2,图4是加约束条件后得到的结果,只保留了一个最优点x=2。
图4(a)为自变量z的寻优结果图,图4(b)为目标函数的变化曲线,图4(c)为目标函数导数的变化曲线。对照图4可以确定最小点位置。最小点的目标函数导数值处于0附近,其对应图4(a)中虚框部分x=2,这时的极小值为f=0,且为全局最小值。
为了比较,下面来看看当取消约束条件时例2中的目标函数的计算结果,参数取为\( \left[k_{i}, \alpha_{i}, I_{0 i}\right. , \left.\mu_{1 i}, \mu_{2 i}, \lambda_{1 i}, \lambda_{2 i}, \lambda_{3 i}, m, n\right]=[1,1,0.5,2,10 , 0.2,0.1,0.08,200,2]\)。寻优结果见图3。这时得到的稳定极小点为0和2,对应的极小值为0。
《图2》

图2 函数曲线
Fig.2 Curve of function
比较图4(a)和图3明显发现系统的运行有了很大改变,加人约丛条件后,脉冲暂态混沌神经网络不再趋向于不符合约束条件的x=0点,说明系统对于约束非线性规划问题是有效的。
《5 结语》
5 结语
脉冲暂态混沌神经网络具有丰富的动力学性质,可以有效地跳出局部最小点。将其应用于求解有约束条件的非线性规划问题时,应用惩罚函数方法,可以将目标函数与约束条件合并成一个表达式,使问题变成一个不含约束条件的非线性规划问题,进而用脉冲暂态混沛神经网络对问题进行求解,经算例证明方法有效。














 京公网安备 11010502051620号
京公网安备 11010502051620号




