《1 前言 》

1 前言 　　

在实际工程问题中，河道水流（如弯道水流、河床变形、丁坝绕流等）通常具有较强的三维特征，因此，研究三维河道水流数学模型有其重要的学术价值。

近数十年来，不少学者对三维河道水流计算方法进行了探讨，已取得了不少研究成果，文献[1]曾做过系统评述。大多数三维模型采用了目前最流行的紊流模型，即基于各向同性的 Boussinesq 紊动粘性假设下的 k－ε 双方程紊流模型，并引用无尺度垂直坐标 σ 坐标，避免了求解三维自由表面的困难。三维模型控制方程通常采用有限体积法数值离散求解，和有限差分法类似，它仅能适应规则边界，但采用平面适体曲线坐标变换，可适应复杂的河道两岸边界形状。文献[2]的解法是目前河道水流的典型解法，也是一种较成功的解法，该文考虑到河道水流各向异性的特点，提出了一种修正的 k－ε 模型，其计算结果与试验能较好吻合。现有的三维河道水流模型的计算工作量很大， k－ε 双方程模型 σ 坐标变换和适体曲线坐标变换的应用，导致了求解方程的非线性化，更进一步增加了计算工作量。

文章研究对象是宽浅河道水流，如长江中下游河道，特别是河口水流，均为潮汐作用下的非恒定流，要求计算时间长，应用现有解法更受一定限制。不同的解法适应不同的流动问题，现有各种解法都有其应用限制， k－ε 双方程模型等所谓精细模型也不例外。为此根据宽浅河道水流特点，笔者等建立了一种简便的更适用于宽浅河道水流的三维数学模型。

《2 浅水紊流模型的建立》

2 浅水紊流模型的建立

《2.1 浅水紊流模型控制方程 》

2.1 浅水紊流模型控制方程  

在 Boussinesq 假设下，考虑各向异性及垂向流速相对较小的假设，浅水河道水流控制方程采用如下形式：

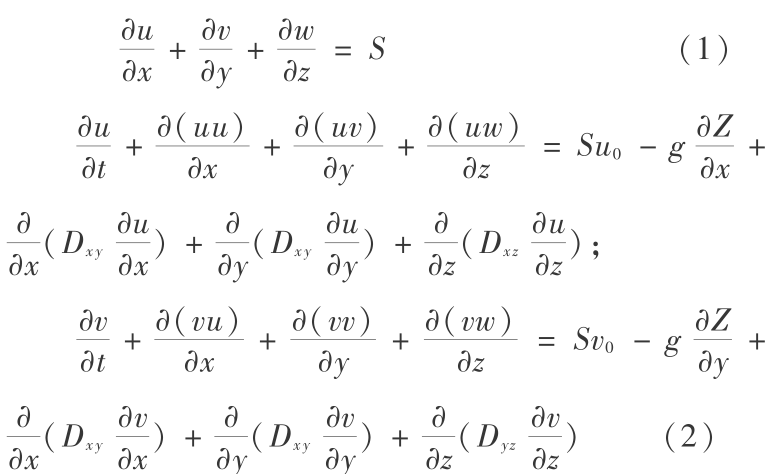
式中 u，v，w 分别为 x，y，z 向流速值；Z 为自由水面高程；S 为单位水体源汇密度，流入为正，流出为负； u0 ， v0 为源汇处设备的进出口流速； Dxy ，Dyz， Dxz 分别为各向紊动黏性系数。

《2.2 紊动粘性系数的确定》

2.2 紊动粘性系数的确定

紊动粘性系数应是空间的函数，求解式（2）首先遇到的困难是如何确定紊动粘性系数。对于浅水流动，显然河底摩阻力 τ0 对水流运动起主要控制作用，找出 τ0 与紊动粘性系数之间关系，由此就可以确定紊动扩散系数的空间分布。根据紊动粘性假设，紊动剪应力 τxz ，τyz 存在如下关系：

由 Prandtl 的混掺理论可导得：

式中 k 为卡门系数，可取 0.4，剪切速度 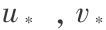由下式表示：

剪切应力沿水深分布可认为接近线性分布，则有：

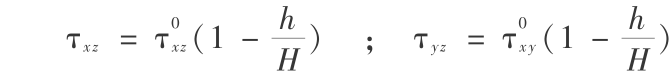
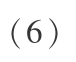
式中 h 为考查点处水深；H 为河床水深。

由式（3）至式（6）则可导得垂向紊动粘性系数的表达式：

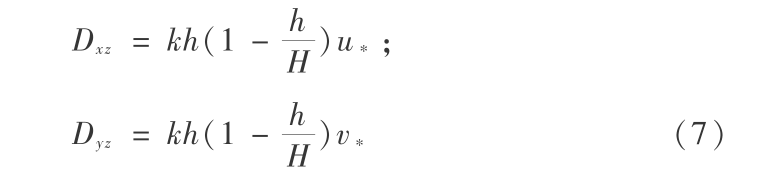
可见垂向紊动粘性系数随水深而变化，河底及水面处为零，0.5H 处具有最大值：

式中，  可用壁函数法或谢才公式确定。由于水平紊动粘性系数对流场影响不大，可简单地由下式决定：

相应物质浓度输运的紊动扩散系数可由下式决定：

通过试算值可取为 1。至此，式（2）和式（7）共同组成了拟建立的三维浅水紊流模型控制方程。它是一个零方程紊流模型，比起双方程紊流模型计算工作量明显减少，它仍反应了紊动粘性系数空间分布的差异，所以其能较好地模拟浅水河道水流的三维特征。

《3 分层积分降维数值解法》

3 分层积分降维数值解法

由于河道水流具有待定的自由表面，导致了求解三维问题的另一困难。对于非恒定流运动，水位随时间变化，通常所谓“刚盖”假设来求解自由表面方法己不适应。笔者曾在 20 世纪 80 年代，受平面二维河道水流数学模型求解自由表面的启发，提出过一种水平分层积分方法，有效地解决了求解三维自由表面的困难[7]。

将平面流场沿水深等分为 N 层，以第 i 层为例，从该层下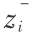表面 至上表面 ，对式（6）和（7）积分：

式（12）积分中，引入了两个假设：

假设一假设被积函数在一层间沿下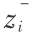表面 至上表面 间是线性分布的。考查通常情况，设被积函数 F，Q 在积分区间内为线性分布，并用下式表示：

因而可计算出如下积分：

式（12）～（16）中上标分别表示 i 层上下表面处值。式（15）即为通常所指由流速沿水深非均匀分布引起的弥散项，在线性分布假设下可用该式算出，这表明假设条件下的积分精度相当于有限元法中的线性单元精度，或有限差分法中前、后差精度，可以满足一般精度要求。

假设二假设各层表面有下列关系：

像边界层模型所作的流速断面分布相似假设那样，认为同一层各垂线上的流速分布符合相似分布假设，则式（17）一定成立。

在以上两个假设前提下，应用牛顿－来布尼斯公式，式（11），（12）积分后可得：

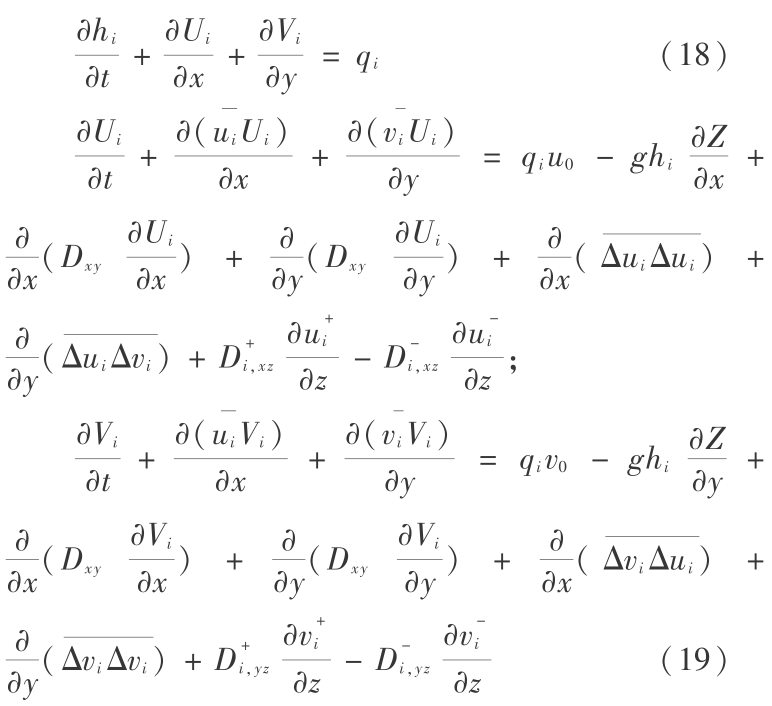
式（19）流速符号顶部“－”表示 i 层垂线平均值，大写相应表示 i 层的单宽流量。由上式可看出，方程形式与平面二维河道水流基本方程相似，是一个典型的二维输运方程，从而把三维问题通过分层积分降维成二维问题，求解二维流场方法可用来求解三维流场。

《4 剖开算子法应用及其数值解》

4 剖开算子法应用及其数值解

通过分层积分，己将三维问题简化为若干个二维问题，而二维问题已有较成熟的解法。二维输运方程是一个混合型算子的输运方程，特别适合应用剖开算子法求解[3 ,4 ,7] 。将方程剖分为不同子算子后，用各自适应的数值解法。

由于存在源汇项，在算子剖开前先将式（19）作适当的变化，化为如下形式：

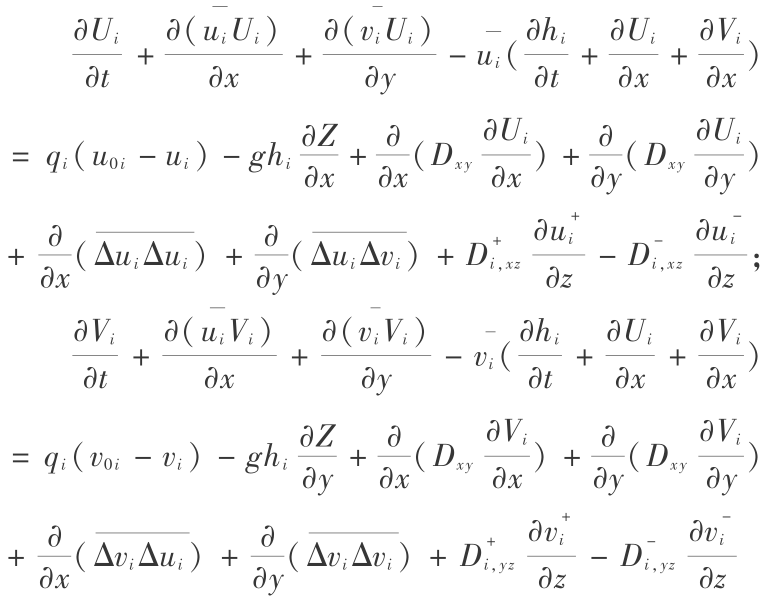
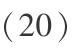
根据算子的性质，将式（20）剖分为如下几个分步，用各自适应的数值方法求解。

《4.1 对流分步》

4.1 对流分步

上式展开后，则可化为典型的纯对流方程

可用文献[3] ，[4]的特征线法求解。

《4.2 压力传播分步》

4.2 压力传播分步

首先对式（18）和（23）对各层求和，则有：

分别对式（24），（25）采用时间前差的隐格式，从而导出自由表面高程 Z 的偏微分方程：

这是二阶常系数微分方程，在复杂平面边界条件下适合应用隐式有限单元法求解。采用加辽金加权余量法，在三角形单元离散条件下，最终可形成线性代数方程组求解，由于它是正定对称的稀疏矩阵，可用 LR 法方便求解。

《4.3 水平扩散分步》

4.3 水平扩散分步

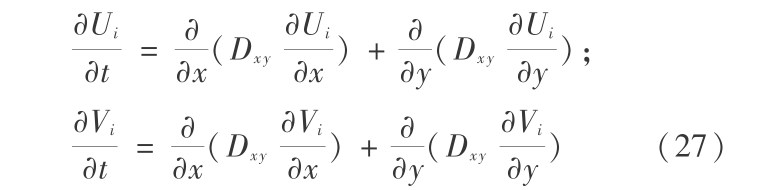
因水平扩散分步数值解法对总计算过程稳定性影响不大，故用显式有限元法求解式（27）。方便起见，式（27）可用通式表示

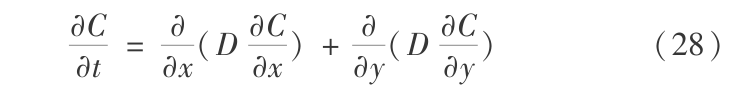
式（28）用显式差分格式表示为

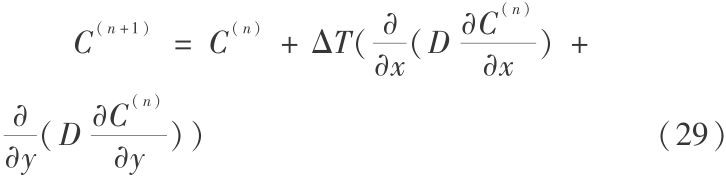
如前所述，采用集中质量有限元法求解式（29）。

《4.4 垂向扩散分步》

4.4 垂向扩散分步

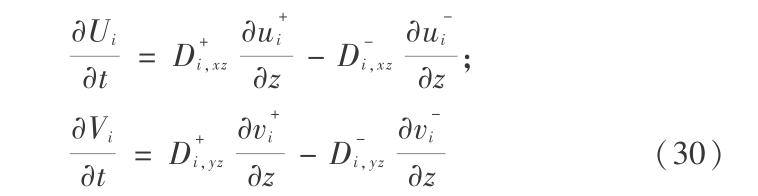
垂向扩散分步的数值解法对计算结果的稳定性影响甚大，上式中没有含（x，y）的导数项，适合用隐式差分法求解，可形成 n 阶三对角线线性方程组求解。

《4.5 源汇及弥散分步》

4.5 源汇及弥散分步

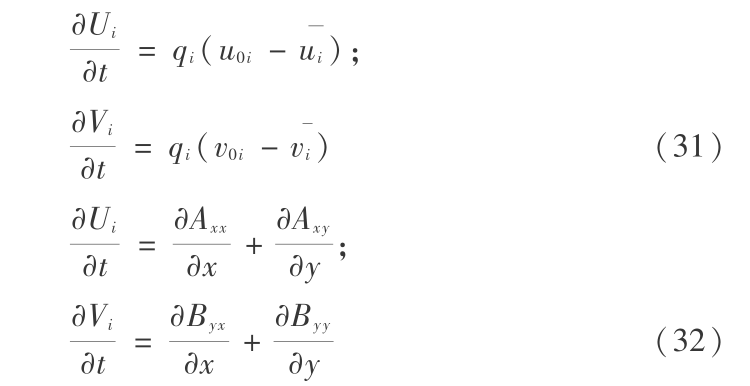
式中

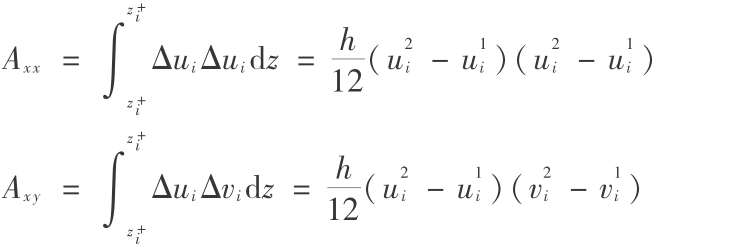
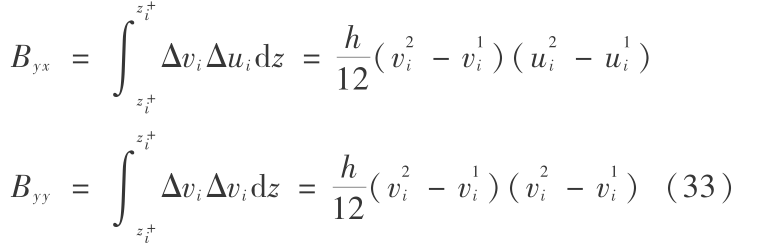
在上述分步中，右边项均未出现二阶以上微分项，因此可用简单的解析法求解。对源汇分步直接积分可得：

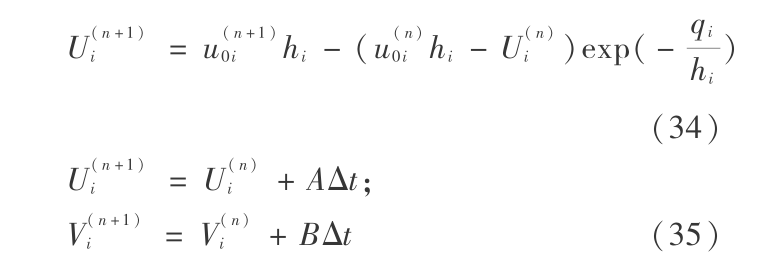
由于单元节点上一阶导数不连续，A，B 由考查点周围相邻的 M 个单元均值给出：

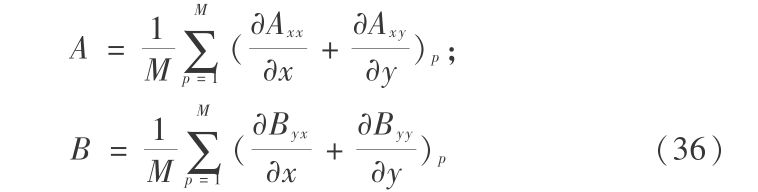
源汇项中 qi 的确定需要说明，实际工程问题中，取排水流量以 Q 给出，它的量纲是 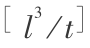，在离散网络下它相当于点源，如源点在 K 点，K 点周围有 M 个单元其他节点值为零，因而有下式守恒关系

则源汇项中 q 由上式求出，量纲是 ，如源点在 i 层，即qi =q ，否则qi 为零。

《5 算例与验证》

5 算例与验证

 “S”形明渠弯道水流具有明显的三维流动特征，文献[5] 曾进行过模型试验研究。选取弯道水流作为算例来验证所建立的三维水流模型，如图 1 所示。

《图1》

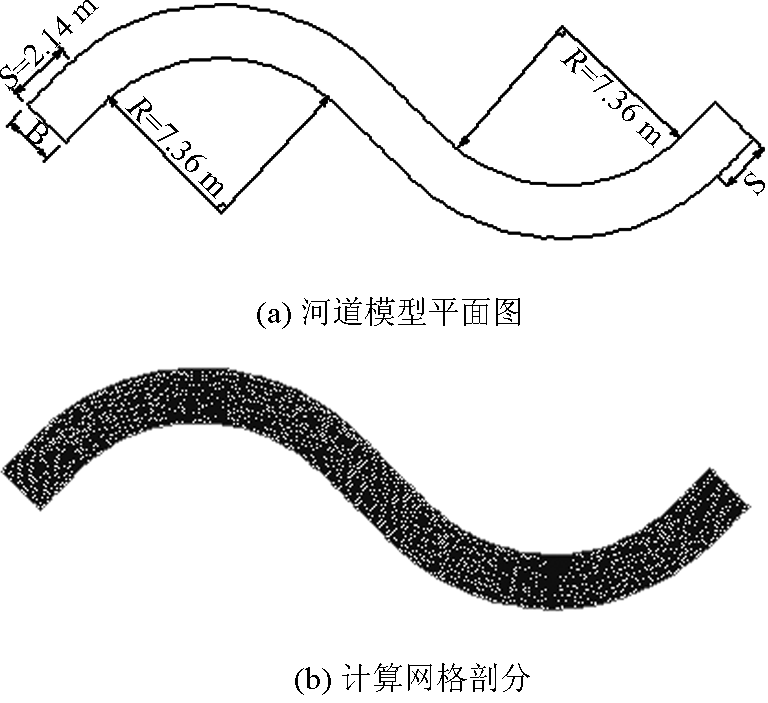
图1 河道模型平面图及计算网格

Fig.1 Sketch of modeling bend flow and computational meshes

模型试验[5] 用光滑材料制成，弯道断面为矩形,宽 B =2.34 m，水深 H =0.115 m，B /H =20.35，可看成宽浅河道，流量 Q =0.098 m3 /s，断面平均流速 u0 =0.366 m /s， Fr =u0 / =0.34，水流为缓流。计算范围与模型试验一致，上游进口为给定流量断面，下游出口为给定水位断面。沿流程共布置 136 个断面，各断面沿河宽布置 13 个节点，平面总离散网络节点为 1 768 个，三角形单元为 3 240 个，沿水深分为 10 层，采用平坡，作为光滑渠道，糙率系数 ks 为 9，相应糙率 n 为 0.01。

用非恒定流过程来逼近恒定流，进口断面给定流量过程，100 s 内由 0 线性升高到 0.098 m3 /s，之后保持不变，经计算 500 s 后，流场内各流动参数不再随时间变化。图 2、图 3 分别为上游进口断面水位 Z 与时间 t 和下游出口断面流量 Q 与时间 t 的计算结果，可见 350 s 后流场趋于稳定，表明该数学模型具有良好的收敛性。

《图2》

图2 进口断面 Z0 ～t 关系

Fig.2 Relationship between Z0 and t at the inlet profile

《图3》

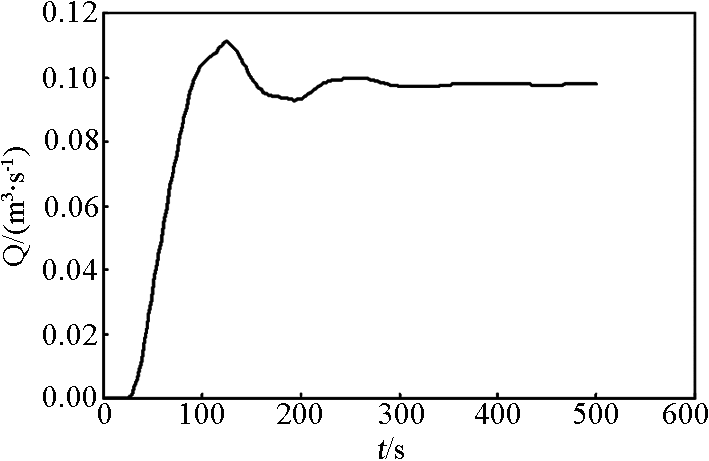
图3 出口断面 Q ～t 关系

Fig.3 Relationship between Q and t at the outlet profile

图 4 给出渠道中心线表层和底层相对径向流速沿程的计算结果。可见虽然进口边界按流速均匀分布给出，但在较短距离内流速调整到河道自然分布状态，面流速大，底流速小，与实际情况完全相符，表明该数学模型有较好仿真能力。图 5 给出渠道中心线表层和底层相对横向流速沿程的计算结果，定义横向流速由近岸指向远岸为正，反之为负。可见在第一弯道上，表层流速为正，底层为负；而在下一个弯道上，表层流速为负，底层为正。表面横向流速总是由凸岸流向凹岸，底层则反之。弯道横向流速最大值达到平均径流速约 30 %，可见弯道产生很强的螺旋流，对弯道河床演变起重要作用。

《图4》

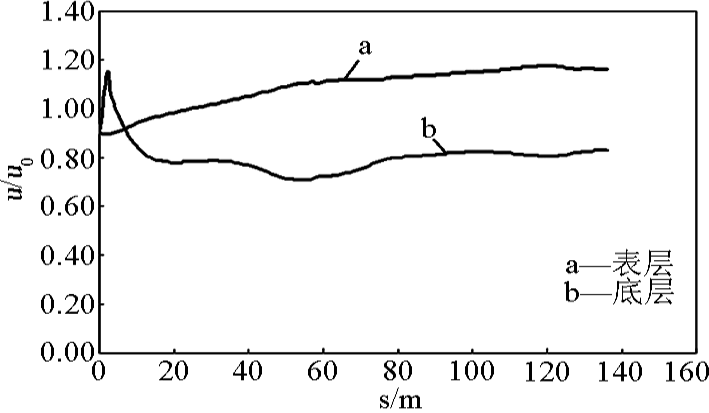
图4 沿中线 u/u0 ~S 变化关系

Fig.4 Relationship of u/u0 with S along the central line

《图5》

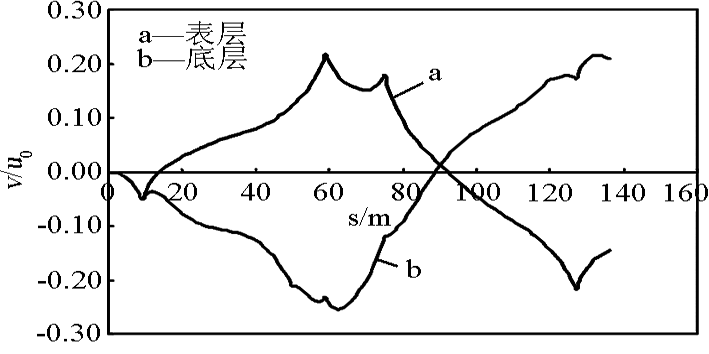
图5 沿中心线 v/u0 ~S 分布

Fig.5 Relationship of v/u0 with S along the central line

7 号断面上沿河宽各条垂线的主流速（径向流速）与断面平均流速比 u/u0 和相对水深 h /H 的关系如图 6 所示，并与文献[6]用非线性 k -ε 双方程模型的计算结果进行了比较。图 7 给出相应垂线相对副流速（横向流速）v/u0 和相对水深 h /H 的关系。 11 号断面上相对主流速、副流速及断面水位沿河宽变化见图 8。可见表层及底层副流速方向相反，也反映了弯道螺旋流的存在。由于弯道离心力作用所致，存在横向水面比降。图 9 分别给出上游弯道局部流场表层及底层的流速分布，可见在近弯道出口横向流速最明显，而不是在弯道中间段，表层流速流向凹岸，底层流速流向凸岸，从而导致凹岸冲凸岸淤的河道冲淤特性。

《图6》

图6 垂线相对主流速与相对水深关系

Fig.6 Relationship of vertical main relative velocity versus the relative water depth

《图7》

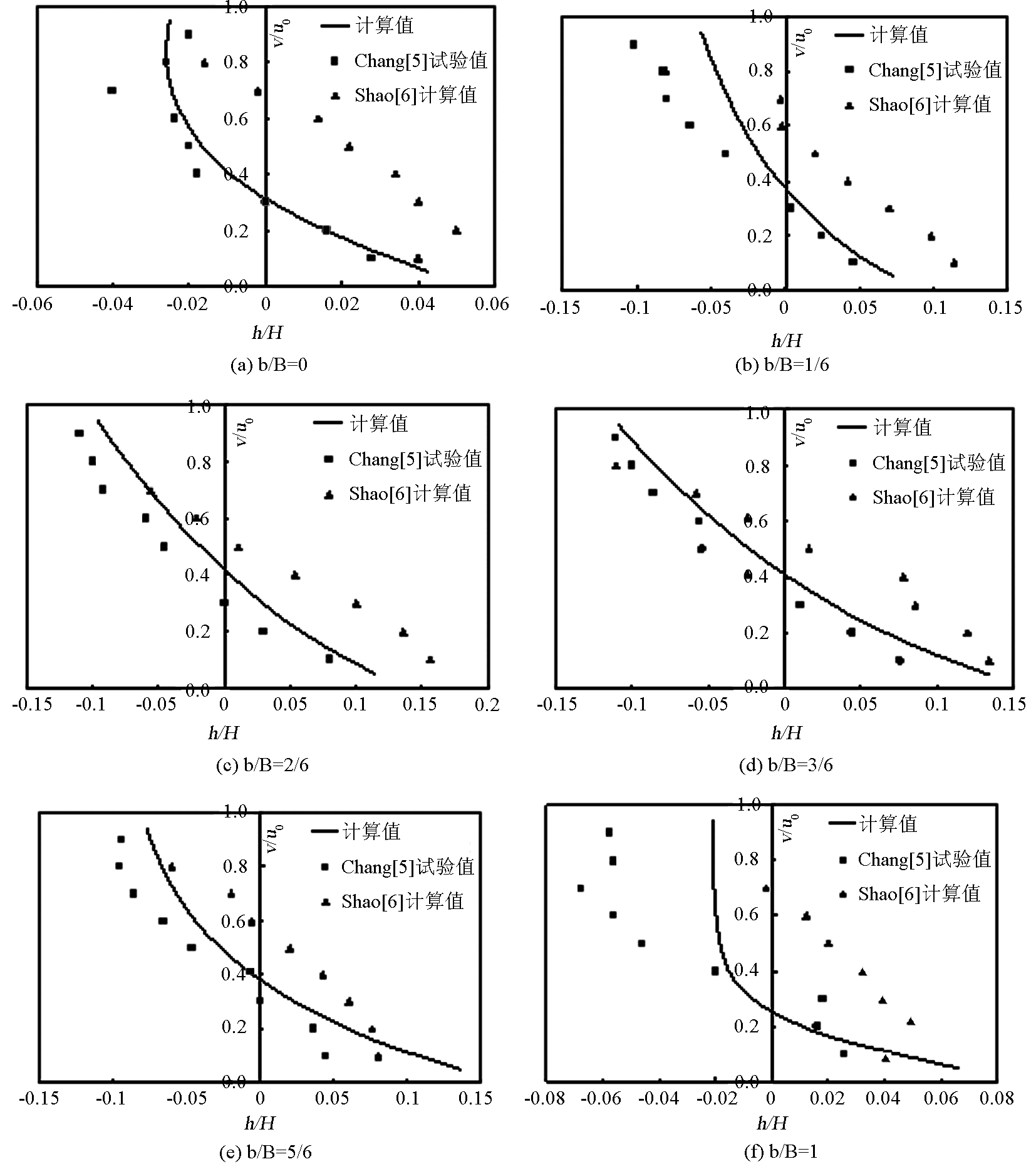
图7 垂线相对副流速与相对水深关系

Fig.7 Relationship of vertical secondary relative velocity versus the relative depth

《图8》

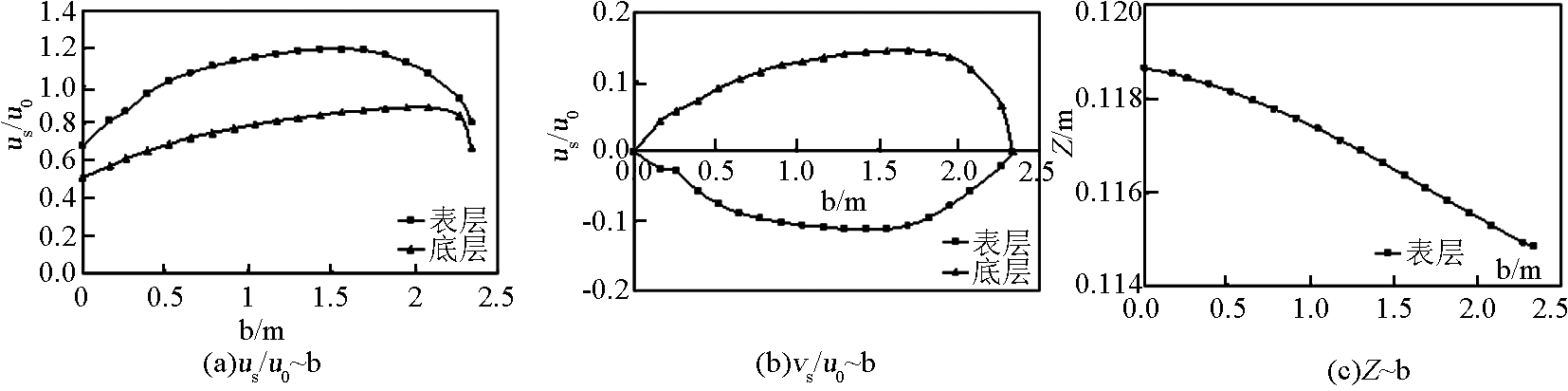
图8 11 号断面沿河宽流速分布

Fig.8 Velocity distribution along the width profile of No.11

《图9》

图9 弯道流场分布

Fig.9 Flow velocity distribution along meandering channel

综上可见，无论是主流速，还是副流速，两者沿垂线变化趋势是比较一致的，在离两岸的河心区域，计算和试验能很好吻合，仅近岸边有较明显误差，相对于文献[6] ，计算精度更高，表明笔者等提出的数学模型计算精度与双方程模型接近。

《6 结语》

6 结语

1）根据宽浅河道水流特点，所提出的零方程紊流模型，计算涉及了垂向紊动扩散系数的沿水深水布特点，故能很好反映三维河道水流特点。

2）提出的分层积分解法，克服了求解三维自由表面的困难，避免了复杂的 σ 坐标变换，而且可将三维问题化为平面二维问题方便求解。

3）用三角形有限元网络离散流场，能较好拟合曲线边界。根据模型方程的混合算子特性，根据不同算子特点，用剖开算子法数值求解，从而具有很好的收敛性。

4）和二方程紊流模型相比，笔者等所提出的零方程模型计算工作量省，特别适合非恒定水流计算。