基于频域的多变量广义预测控制（MIMO-GPC）稳定性分析

摘要

提出了基于频域的多变量广义预测控制（MIMO-GPC）稳定性分析方法，推导了MIMO-GPC的闭环反馈结构，给出了基于闭环特征多项式的MIMO-GPC的稳定性判据和奈奎斯特稳定性判据。这些判据可作为MIMO-GPC控制器参数设计的重要依据。

正文

《1 引言》

1 引言

广义预测控制 (GPC) ^[1]算法很快就由单输入单输出 (SISO) 扩展到了多输入多输出的系统 (MIMO-GPC) , 并且在系统自适应能力、去耦合作用等方面取得良好的效果。已大量的用于多变量的复杂工业控制现场。

在实际应用中, 一方面改进算法, 提高其运算速度, 如多变量广义预测控制的直接算法。另一方面人们在分析其稳定性和鲁棒性方面也作了大量的工作^[2], 这些分析大多是基于离散的时间域进行的, 笔者在推导MIMO-GPC闭环反馈结构的基础上, 提出了基于频域的MIMO-GPC稳定性分析方法。

《2 MIMO-GPC算法描述》

2 MIMO-GPC算法描述

多变量GPC控制算法描述如下:

$A (z^{- 1}) Δ y (k) = B (z^{- 1}) Δ u (k - 1) (1)$ $A (z^{- 1}) Δ y (k) = B (z^{- 1}) Δ u (k - 1) (1)$

其中:

$\begin{array}{l} A (z^{- 1}) = Ι + A_{1} z^{- 1} + \dots + A_{n_{a}} z^{- n_{a}} (2) \\ B (z^{- 1}) = B_{0} + B_{1} z^{- 1} + \dots + B_{n_{b}} z^{- n_{b}} (3) \end{array}$ $\begin{array}{l} A (z^{- 1}) = Ι + A_{1} z^{- 1} + \dots + A_{n_{a}} z^{- n_{a}} (2) \\ B (z^{- 1}) = B_{0} + B_{1} z^{- 1} + \dots + B_{n_{b}} z^{- n_{b}} (3) \end{array}$

y (k) 和u (k) 分别表示系统在当前的被控对象和控制量, n×1维向量。

MIMO-GPC的目标函数为

$\begin{array}{l} J = \sum_{j = 1}^{Ν} ∥ \hat{y} (k + j | k) - w (k + j) ∥^{2} + \\ Λ \sum_{j = 1}^{Ν_{u}} ∥ Δ u (k + j - 1) ∥^{2} (4) \end{array}$ $\begin{array}{l} J = \sum_{j = 1}^{Ν} ∥ \hat{y} (k + j | k) - w (k + j) ∥^{2} + \\ Λ \sum_{j = 1}^{Ν_{u}} ∥ Δ u (k + j - 1) ∥^{2} (4) \end{array}$

其中 ${\hat{y} (k + j | k)}$ ${\hat{y} (k + j | k)}$ 为y (k) 的前向j步预测序列, N为预测步长, N_u为控制步长, Λ=diag (λ₁, …, λ_n) 为控制加权因子, {w (k+j) }为要跟踪的设定值柔化序列, 由如下动态方程产生:

$\begin{array}{l} w (k) = y (k), \\ w (k + j) = α w (k + j - 1) + α^{'} y_{r} (k), \\ j = 1, \dots, Ν (5) \end{array}$ $\begin{array}{l} w (k) = y (k), \\ w (k + j) = α w (k + j - 1) + α^{'} y_{r} (k), \\ j = 1, \dots, Ν (5) \end{array}$

其中α=diag {α₁, …, α_n}为柔化因子对角阵, α′=diag {1-α₁, …, 1-α_n}, y_r (k) 为当前设定值。

为得到输出的向前第j步预测值 $\hat{y} (k + j | k)$ $\hat{y} (k + j | k)$ , 需要求解如下两组丢番图方程:

$\begin{array}{l} Ι = E^{'}_{j} (z^{- 1}) A (z^{- 1}) Δ + z^{- j} F_{j} (z^{- 1}), \\ j = 1, \dots, Ν (6) \\ E^{'}_{j} (z^{- 1}) B (z^{- 1}) = G^{'}_{j} (z^{- 1}) + z^{- j} Η_{j} (z^{- 1}), \\ j = 1, \dots, Ν (7) \end{array}$ $\begin{array}{l} Ι = E^{'}_{j} (z^{- 1}) A (z^{- 1}) Δ + z^{- j} F_{j} (z^{- 1}), \\ j = 1, \dots, Ν (6) \\ E^{'}_{j} (z^{- 1}) B (z^{- 1}) = G^{'}_{j} (z^{- 1}) + z^{- j} Η_{j} (z^{- 1}), \\ j = 1, \dots, Ν (7) \end{array}$

其中:

$\begin{array}{l} E^{'}_{j} (z^{- 1}) = E_{0} + E_{1} z^{- 1} + \dots + E_{j - 1} z^{- (j - 1)} (8) \\ F_{j} (z^{- 1}) = F_{j 0} + F_{j 1} z^{- 1} + \dots + F_{j n_{a}} z^{- n_{a}} (9) \\ G^{'}_{j} (z^{- 1}) = G_{0} + G_{1} z^{- 1} + \dots + G_{j - 1} z^{- (j - 1)} (10) \\ Η_{j} (z^{- 1}) = Η_{j 0} + Η_{j 1} z^{- 1} + \dots + Η_{j n_{b} - 1} z^{- (n_{b} - 1)} (11) \\ Δ = 1 - z^{- 1} 。 \end{array}$ $\begin{array}{l} E^{'}_{j} (z^{- 1}) = E_{0} + E_{1} z^{- 1} + \dots + E_{j - 1} z^{- (j - 1)} (8) \\ F_{j} (z^{- 1}) = F_{j 0} + F_{j 1} z^{- 1} + \dots + F_{j n_{a}} z^{- n_{a}} (9) \\ G^{'}_{j} (z^{- 1}) = G_{0} + G_{1} z^{- 1} + \dots + G_{j - 1} z^{- (j - 1)} (10) \\ Η_{j} (z^{- 1}) = Η_{j 0} + Η_{j 1} z^{- 1} + \dots + Η_{j n_{b} - 1} z^{- (n_{b} - 1)} (11) \\ Δ = 1 - z^{- 1} 。 \end{array}$

当B (z^-1) =B₀时, H_j (z^-1) =0, 此时G′_j (z^-1) =B₀E′_j (z^-1) 该丢番图方程递推解为:

$\begin{array}{l} E^{'}_{j} (z^{- 1}) = Ι ‚ F_{1} (z^{- 1}) = z [Ι - \bar{A} (z^{- 1})] ‚ \\ \bar{A} (z^{- 1}) = A (z^{- 1}) Δ (12) \\ E^{'}_{j + 1} (z^{- 1}) = E^{'}_{j} (z^{- 1}) + r_{j} z^{- j} ‚ \\ F_{j + 1} (z^{- 1}) = z [F_{j} (z^{- 1}) - r_{j} \bar{A} (z^{- 1})], \\ j = 1, \dots, Ν (13) \\ r_{j} = F_{j 0} (14) \end{array}$ $\begin{array}{l} E^{'}_{j} (z^{- 1}) = Ι ‚ F_{1} (z^{- 1}) = z [Ι - \bar{A} (z^{- 1})] ‚ \\ \bar{A} (z^{- 1}) = A (z^{- 1}) Δ (12) \\ E^{'}_{j + 1} (z^{- 1}) = E^{'}_{j} (z^{- 1}) + r_{j} z^{- j} ‚ \\ F_{j + 1} (z^{- 1}) = z [F_{j} (z^{- 1}) - r_{j} \bar{A} (z^{- 1})], \\ j = 1, \dots, Ν (13) \\ r_{j} = F_{j 0} (14) \end{array}$

将式 (1) 两边左乘E′_j (z^-1) , 得

$\begin{array}{l} E^{'}_{j} (z^{- 1}) A (z^{- 1}) Δ y (k) = \\ E^{'}_{j} (z^{- 1}) B (z^{- 1}) Δ u (k - 1) (15) \end{array}$ $\begin{array}{l} E^{'}_{j} (z^{- 1}) A (z^{- 1}) Δ y (k) = \\ E^{'}_{j} (z^{- 1}) B (z^{- 1}) Δ u (k - 1) (15) \end{array}$

将式 (6) 和式 (7) 式代入式 (15) 得

$\begin{array}{l} y (k) = G^{'}_{j} (z^{- 1}) Δ u (k - 1) + F_{j} (z^{- 1}) y (k - j) + \\ Η_{j} (z^{- 1}) Δ u (k - j - 1) (16) \end{array}$ $\begin{array}{l} y (k) = G^{'}_{j} (z^{- 1}) Δ u (k - 1) + F_{j} (z^{- 1}) y (k - j) + \\ Η_{j} (z^{- 1}) Δ u (k - j - 1) (16) \end{array}$

于是得到y (k) 的前向预测

$\begin{array}{l} \hat{y} (k + j | k) = G^{'}_{j} (z^{- 1}) Δ u (k + j - 1) + \\ F_{j} (z^{- 1}) y (k) + Η_{j} (z^{- 1}) Δ u (k - 1) (17) \end{array}$ $\begin{array}{l} \hat{y} (k + j | k) = G^{'}_{j} (z^{- 1}) Δ u (k + j - 1) + \\ F_{j} (z^{- 1}) y (k) + Η_{j} (z^{- 1}) Δ u (k - 1) (17) \end{array}$

令:

$Y = [\hat{y} (k + j$ $Y = [\hat{y} (k + j$ $k)^{Τ}, \dots, \hat{y} (k + Ν$ $k)^{Τ}, \dots, \hat{y} (k + Ν$ k) ^T]^T,

$\begin{array}{l} Δ U = [Δ u (k)^{Τ}, \dots, Δ u (k + Ν_{u} - 1)^{Τ}]^{Τ}, \\ F (z^{- 1}) = [F_{1} (z^{- 1})^{Τ}, \dots, F_{Ν} (z^{- 1})^{Τ}], \\ Η (z^{- 1}) = [Η_{1} (z^{- 1})^{Τ}, \dots, Η_{Ν} (z^{- 1})^{Τ}], \\ W = [w (k + 1)^{Τ}, \dots, w (k + Ν)^{Τ}]^{Τ}, \\ G = [\begin{matrix} G_{0} & 0 & \dots & 0 \\ G_{1} & G_{0} & \dots & 0 \\ ⋮ & ⋮ & ⋮ \\ G_{Ν_{u} - 1} & G_{Ν_{u} - 2} & \dots & G_{0} \\ ⋮ & ⋮ & ⋮ \\ G_{Ν - 1} & G_{Ν - 2} & \dots & G_{Ν - Ν_{u}} \end{matrix}] 。 \end{array}$ $\begin{array}{l} Δ U = [Δ u (k)^{Τ}, \dots, Δ u (k + Ν_{u} - 1)^{Τ}]^{Τ}, \\ F (z^{- 1}) = [F_{1} (z^{- 1})^{Τ}, \dots, F_{Ν} (z^{- 1})^{Τ}], \\ Η (z^{- 1}) = [Η_{1} (z^{- 1})^{Τ}, \dots, Η_{Ν} (z^{- 1})^{Τ}], \\ W = [w (k + 1)^{Τ}, \dots, w (k + Ν)^{Τ}]^{Τ}, \\ G = [\begin{matrix} G_{0} & 0 & \dots & 0 \\ G_{1} & G_{0} & \dots & 0 \\ ⋮ & ⋮ & ⋮ \\ G_{Ν_{u} - 1} & G_{Ν_{u} - 2} & \dots & G_{0} \\ ⋮ & ⋮ & ⋮ \\ G_{Ν - 1} & G_{Ν - 2} & \dots & G_{Ν - Ν_{u}} \end{matrix}] 。 \end{array}$

则有:

$Y = G Δ U + F (z^{- 1}) y (k) + Η (z^{- 1}) Δ u (k - 1) (18)$ $Y = G Δ U + F (z^{- 1}) y (k) + Η (z^{- 1}) Δ u (k - 1) (18)$

目标函数为:

$J = ∥ Y - W ∥^{2} + ∥ Δ U ∥_{Λ}^{2}, (19)$ $J = ∥ Y - W ∥^{2} + ∥ Δ U ∥_{Λ}^{2}, (19)$

将式 (18) 代入式 (19) , 令 ∂J/∂Δu=0, 得控制律:

$\begin{array}{l} Δ U = (G^{Τ} G + Λ)^{- 1} G^{Τ} (W - F (z^{- 1}) y (k) - \\ Η (z^{- 1}) Δ u (k - 1)) (20) \end{array}$ $\begin{array}{l} Δ U = (G^{Τ} G + Λ)^{- 1} G^{Τ} (W - F (z^{- 1}) y (k) - \\ Η (z^{- 1}) Δ u (k - 1)) (20) \end{array}$

(G^TG+Λ) ^-1G^T的前N行为P^T=[P₁, …, P_N]。其中P_j (j=1, …, N) 是n×n矩阵。于是, 式 (18) 可写为

$\begin{array}{l} Δ u (k) = Ρ^{Τ} (W - F (z^{- 1}) y (k) - \\ z^{- 1} Η (z^{- 1}) Δ u (k)) (21) \end{array}$ $\begin{array}{l} Δ u (k) = Ρ^{Τ} (W - F (z^{- 1}) y (k) - \\ z^{- 1} Η (z^{- 1}) Δ u (k)) (21) \end{array}$

《3 MIMO-GPC 闭环反馈系统》

3 MIMO-GPC 闭环反馈系统

将上节结果进一步推导如下:

由式 (5) 可知

$W = F_{α} y (k) + \bar{F}_{α} y_{r} (k) (22)$ $W = F_{α} y (k) + \bar{F}_{α} y_{r} (k) (22)$

其中

$\begin{array}{l} F_{α} = [α, α^{2}, \dots, α^{Ν}]^{Τ}, \\ \bar{F}_{α} = [Ι - α, Ι - α^{2}, \dots, Ι - α^{Ν}]^{Τ} 。 \\ α^{2} = d i a g {α_{1}^{2} \dots α_{n}^{2}}, \dots, α^{Ν} = d i a g {α_{1}^{Ν} \dots α_{n}^{Ν}} \end{array}$ $\begin{array}{l} F_{α} = [α, α^{2}, \dots, α^{Ν}]^{Τ}, \\ \bar{F}_{α} = [Ι - α, Ι - α^{2}, \dots, Ι - α^{Ν}]^{Τ} 。 \\ α^{2} = d i a g {α_{1}^{2} \dots α_{n}^{2}}, \dots, α^{Ν} = d i a g {α_{1}^{Ν} \dots α_{n}^{Ν}} \end{array}$

得

$Δ u (k) = Ρ^{Τ} [\bar{F}_{α} y_{r} (k) - (F (z^{- 1}) - F_{α}) y (k)] (23)$ $Δ u (k) = Ρ^{Τ} [\bar{F}_{α} y_{r} (k) - (F (z^{- 1}) - F_{α}) y (k)] (23)$

可得

$Τ (z^{- 1}) Δ u (k) = R y_{r} (k) - S (z^{- 1}) y (k) (24)$ $Τ (z^{- 1}) Δ u (k) = R y_{r} (k) - S (z^{- 1}) y (k) (24)$

其中

$\begin{array}{l} Τ (z^{- 1}) = Ι + z^{- 1} Ρ^{Τ} \bar{Η} (z^{- 1}) (25) \\ R = Ρ^{Τ} \bar{F}_{α} (26) \\ S (z^{- 1}) = (Ρ^{Τ} F (z^{- 1}) - F_{α}) (27) \end{array}$ $\begin{array}{l} Τ (z^{- 1}) = Ι + z^{- 1} Ρ^{Τ} \bar{Η} (z^{- 1}) (25) \\ R = Ρ^{Τ} \bar{F}_{α} (26) \\ S (z^{- 1}) = (Ρ^{Τ} F (z^{- 1}) - F_{α}) (27) \end{array}$

由式 (1) 得

$Δ u (k) = z B^{- 1} (z^{- 1}) A (z^{- 1}) Δ y (k) (28)$ $Δ u (k) = z B^{- 1} (z^{- 1}) A (z^{- 1}) Δ y (k) (28)$

将 (28) 式代入 (24) , 得

$\begin{array}{l} z Τ (z^{- 1}) B^{- 1} (z^{- 1}) A (z^{- 1}) Δ y (k) = \\ R y_{r} (k) - S (z^{- 1}) y (k) (29) \end{array}$ $\begin{array}{l} z Τ (z^{- 1}) B^{- 1} (z^{- 1}) A (z^{- 1}) Δ y (k) = \\ R y_{r} (k) - S (z^{- 1}) y (k) (29) \end{array}$

或

$\begin{array}{l} (z Τ (z^{- 1}) B^{- 1} (z^{- 1}) A (z^{- 1}) Δ + \\ S (z^{- 1})) B (z^{- 1}) B^{- 1} (z^{- 1}) y (k) = R y_{r} (k) (30) \end{array}$ $\begin{array}{l} (z Τ (z^{- 1}) B^{- 1} (z^{- 1}) A (z^{- 1}) Δ + \\ S (z^{- 1})) B (z^{- 1}) B^{- 1} (z^{- 1}) y (k) = R y_{r} (k) (30) \end{array}$

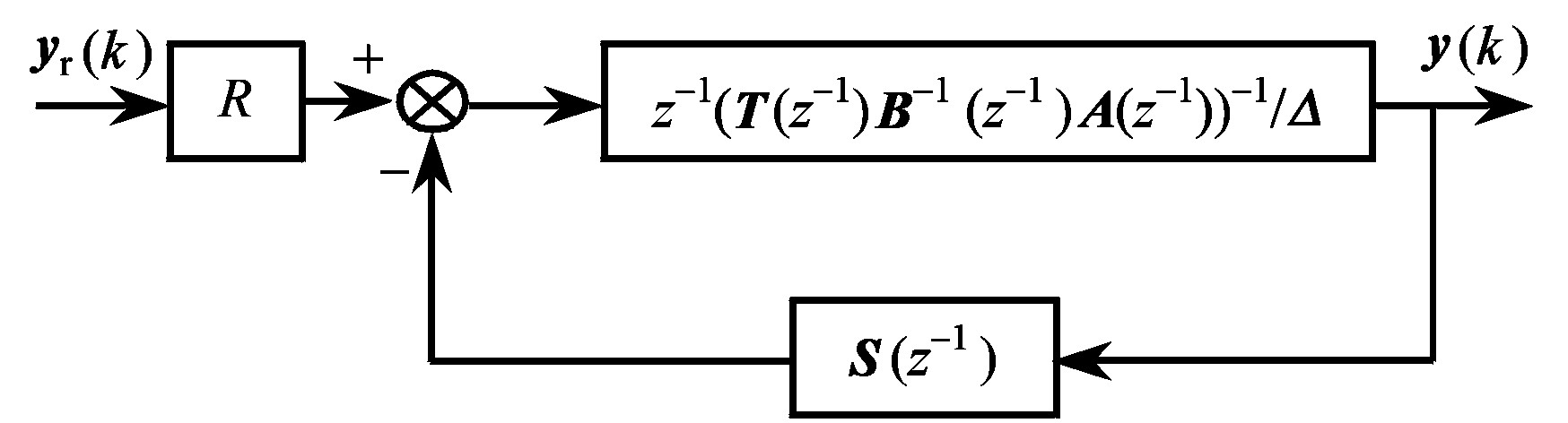
由式 (28) 可得MIMO-GPC闭环反馈结构框图, 如图1所示。闭环传递函数可表示为:

$\begin{array}{l} G^{*} (z^{- 1}) = (z Τ (z^{- 1}) B^{- 1} (z^{- 1}) A (z) Δ + \\ S (z^{- 1}))^{- 1} R (31) \end{array}$ $\begin{array}{l} G^{*} (z^{- 1}) = (z Τ (z^{- 1}) B^{- 1} (z^{- 1}) A (z) Δ + \\ S (z^{- 1}))^{- 1} R (31) \end{array}$

《图1》

图1MIMO-GPC反馈结构框图

Fig.1 Structure of MIMO-GPC

《4 多变量系统的特性和频域稳定性判据》

4 多变量系统的特性和频域稳定性判据

《4.1多变量反馈系统的基本结构和相关矩阵》

4.1多变量反馈系统的基本结构和相关矩阵

通常图1所示闭环子系统都可化为图2的形式

$\begin{array}{l} Η (s) = Q (s) [Ι_{r} + F (s) Q (s)]^{- 1} = \\ Q (s) D_{e}^{- 1} (s) (32) \end{array}$ $\begin{array}{l} Η (s) = Q (s) [Ι_{r} + F (s) Q (s)]^{- 1} = \\ Q (s) D_{e}^{- 1} (s) (32) \end{array}$

或

$\begin{array}{l} Η (s) = [Ι_{m} + Q (s) F (s)]^{- 1} Q (s) = \\ D_{y}^{- 1} (s) Q (s) (33) \end{array}$ $\begin{array}{l} Η (s) = [Ι_{m} + Q (s) F (s)]^{- 1} Q (s) = \\ D_{y}^{- 1} (s) Q (s) (33) \end{array}$

《图2》

图2闭环反馈结构框图

Fig.2 Structure of closed-loop feedback

当det Q (s) ≠0时, H (s) 必定为非奇异矩阵, 它的逆为

$\begin{array}{l} Η^{- 1} (s) = {[Ι_{m} + Q (s) F (s)]^{- 1} Q (s)}^{- 1} = \\ Q^{- 1} (s) [Ι_{m} + Q (s) F (s)] = Q^{- 1} (s) + F (s) (34) \end{array}$ $\begin{array}{l} Η^{- 1} (s) = {[Ι_{m} + Q (s) F (s)]^{- 1} Q (s)}^{- 1} = \\ Q^{- 1} (s) [Ι_{m} + Q (s) F (s)] = Q^{- 1} (s) + F (s) (34) \end{array}$

对式 (32) 至式 (34) 的两端分别求行列式, 可推导出回差矩阵行列式的几个关系如下:

$\begin{array}{l} \det [Ι_{r} + F (s) Q (s)] = \det Q (s) / \det Η (s) = \\ \det Η^{- 1} (s) / \det Q^{- 1} (s) = \det [Q^{- 1} (s) + \\ F (s)] / \det Q^{- 1} (s) = \det [Ι_{m} + Q (s) F (s)] (35) \end{array}$ $\begin{array}{l} \det [Ι_{r} + F (s) Q (s)] = \det Q (s) / \det Η (s) = \\ \det Η^{- 1} (s) / \det Q^{- 1} (s) = \det [Q^{- 1} (s) + \\ F (s)] / \det Q^{- 1} (s) = \det [Ι_{m} + Q (s) F (s)] (35) \end{array}$

令闭环特征多项式为ρ_c (s) , 开环特征多项式为ρ_o (s) 。可得

$\begin{array}{l} ρ_{c} (s) / ρ_{o} (s) = \det [Ι_{m} + Q (s) F (s)] = \\ \det [Ι_{r} + F (s) Q (s)] (36) \end{array}$ $\begin{array}{l} ρ_{c} (s) / ρ_{o} (s) = \det [Ι_{m} + Q (s) F (s)] = \\ \det [Ι_{r} + F (s) Q (s)] (36) \end{array}$

《4.2多变量闭环系统频域稳定性判据》

4.2多变量闭环系统频域稳定性判据

作为单变量系统稳定的充分必要条件, 特征多项式在右半平面无零点。可把这个概念扩充到多变量系统。

对于图2系统, 开环稳定的充要条件是开环特征多项式ρ_o (s) 的全部零点都位于复平面的开左半平面上。

同理, 该系统闭环稳定的充分必要要条件是闭环特征多项式ρ_c (s) 的全部零点都位于复平面的开左半平面上。

开环特征多项式ρ_o (s) 、闭环特征多项式ρ_c (s) 和回差矩阵行列式存在如下关系式^[3]。

$\begin{array}{l} \frac{ρ_{c} (s)}{ρ_{o} (s)} = \det [Ι_{m} + Q (s) F (s)] = \\ \prod_{i = 1}^{n} (s - a^{'}_{i}) / \prod_{j = 1}^{n}) (s - a_{j}) (37) \end{array}$ $\begin{array}{l} \frac{ρ_{c} (s)}{ρ_{o} (s)} = \det [Ι_{m} + Q (s) F (s)] = \\ \prod_{i = 1}^{n} (s - a^{'}_{i}) / \prod_{j = 1}^{n}) (s - a_{j}) (37) \end{array}$

式中a′_i是闭环特征多项式ρ_c (s) 的零点, 也就是系统的闭环极点。a′_i是开环特征多项式ρ_o (s) 的零点, 也就是系统的开环极点。因此, 只要求得回差矩阵行列式, 就可计算系统的开环极点和闭环极点, 进而分析系统的稳定性。

在介绍多变量系统的奈奎斯特图之前, 首先定义D型围线, 它是以半径无穷大的半圆顺时针包围右半复平面一周所形成的围线。如果在此围线上有传递函数的极点, 则以半径为无穷小的半圆从右侧绕过。这样得到的围线成为D型围线。

多变量系统的奈奎斯特图可描述如下^[3]:设矩阵D (s) 为非奇异方阵, 它的行列式det D (s) 就是s的标量函数。当s沿D型围线变化一周时, 函数det D (s) 在复平面上划出一条闭合曲线, 这条曲线称为det D (s) 的奈奎斯特图。这条闭合曲线顺时针包围复平面上坐标为a+jb的点A的周数称为函数矩阵D (s) 关于A点的周数, 记为

$e n c (D (s), a + j b) (38)$ $e n c (D (s), a + j b) (38)$

或

$e n c (D (s), A) (39)$ $e n c (D (s), A) (39)$

如果A点是原点, 上述周函数也可简记为

$e n c D (s) (40)$ $e n c D (s) (40)$

并简称为D (s) 的周函数。

多变量系统的Nyquist稳定判据可描述如下:设开环特征多项式ρ_o (s) 在右半s平面上有n₀个零点, 则闭环系统稳定的充分必要条件是

$e n c D (s) = - n_{0} (41)$ $e n c D (s) = - n_{0} (41)$

其中D (s) 为系统的回差矩阵。

根据从s平面到z平面的映射关系, 不难得出多变量离散系统的稳定性判据。离散控制系统稳定的充分必要条件是:

当且仅当离散特征方程的全部特征根均分布在z平面上的单位圆内, 或者特征根的模均小于1, 相应的离散系统是稳定的。

同样, 多变量离散系统的Nyquist稳定判据可描述如下:设开环特征多项式ρ_o (s) 在z平面的单位圆外上有n₀个零点, 则闭环系统稳定的充分必要条件是

$e n c D (z) = - n_{0} (42)$ $e n c D (z) = - n_{0} (42)$

上述判据可用于MIMO-GPC稳定性分析。

《5 基于频域的MIMO-GPC算法稳定性判据》

5 基于频域的MIMO-GPC算法稳定性判据

将图1中闭环反馈部分的前馈通路定义为

$Q (z^{- 1}) = z^{- 1} (Τ (z^{- 1}) B^{- 1} (z^{- 1}) A (z^{- 1}))^{- 1} / Δ (43)$ $Q (z^{- 1}) = z^{- 1} (Τ (z^{- 1}) B^{- 1} (z^{- 1}) A (z^{- 1}))^{- 1} / Δ (43)$

因为图1中的R为一常数阵, 在稳定性分析中可只考虑闭环回路中Q (z^-1) , S (z^-1) 的作用。系统的回差矩阵D (z^-1) 可表示为

$D (z^{- 1}) = Ι + Q (z^{- 1}) S (z^{- 1}) (44)$ $D (z^{- 1}) = Ι + Q (z^{- 1}) S (z^{- 1}) (44)$

开环特征多项式ρ_o (z^-1) 、闭环特征多项式ρ_c (z^-1) 和回差矩阵行列式存在如下关系式:

$\begin{array}{l} ρ_{c} (z^{- 1}) / ρ_{o} (z^{- 1}) = \\ \det [Ι + Q (z^{- 1}) S (z^{- 1})] = \det D (z^{- 1}) (45) \end{array}$ $\begin{array}{l} ρ_{c} (z^{- 1}) / ρ_{o} (z^{- 1}) = \\ \det [Ι + Q (z^{- 1}) S (z^{- 1})] = \det D (z^{- 1}) (45) \end{array}$

因此det D (z^-1) 的极点为开环特征多项式ρ_o (z^-1) 的根, 零点为闭环特征多项式ρ_c (z^-1) 的根。

可以由MIMO-GPC的闭环反馈结构和回差矩阵, 对MIMO-GPC进行稳定性分析, 提出了稳定性定理1。

定理1 多输入多输出的广义预测控制器闭环反馈结构如图2, 系统稳定的充要条件是回差矩阵行列式

$\det D (z^{- 1}) = \det [Ι + Q (z^{- 1}) S (z^{- 1})]$ $\det D (z^{- 1}) = \det [Ι + Q (z^{- 1}) S (z^{- 1})]$

的零点均分布在z平面上的单位圆内, 即回差矩阵行列式零点的模均小于1, 或回差矩阵行列式分子多项式为Hurwitz多项式。

基于离散域内判别系统稳定性的奈奎斯特判据, 提出了MIMO-GPC系统基于频域的稳定性定理2。

定理2 多输入多输出的广义预测控制器闭环反馈结构如图2, 设回差矩阵行列式在单位圆外的根的个数为 $\tilde{Ρ}$ $\tilde{Ρ}$ , 则闭环系统稳定的充要条件是

$e n c [Ι + Q (z^{- 1}) S (z^{- 1})] = - \tilde{Ρ},$ $e n c [Ι + Q (z^{- 1}) S (z^{- 1})] = - \tilde{Ρ},$

即回差矩阵行列式

$\det D (z^{- 1}) = \det [Ι + Q (z^{- 1}) S (z^{- 1})]$ $\det D (z^{- 1}) = \det [Ι + Q (z^{- 1}) S (z^{- 1})]$

的奈奎斯特曲线逆时针绕原点的圈数为 $\tilde{Ρ}$ $\tilde{Ρ}$ 。

应用定理1和定理2, 可以形象直观地对多变量广义预测控制进行定量的稳定性分析, 并指导控制器参数设计。

《6 仿真研究》

6 仿真研究

对如下两变量系统进行仿真:

$\begin{array}{l} [\begin{matrix} 1 - 1.5 z^{- 1} + 0.48 z^{- 2} & - 0.2 z^{- 1} + 0.1 z^{- 2} \\ - 0.1 z^{- 1} & 1 - 0.9 z^{- 1} + 0.2 z^{- 2} \end{matrix}] \cdot \\ Δ y (k) = [\begin{matrix} 1 + 1.5 z^{- 1} & z^{- 1} \\ 0 & 1 + z^{- 1} \end{matrix}] Δ u (k - 1) (46) \end{array}$ $\begin{array}{l} [\begin{matrix} 1 - 1.5 z^{- 1} + 0.48 z^{- 2} & - 0.2 z^{- 1} + 0.1 z^{- 2} \\ - 0.1 z^{- 1} & 1 - 0.9 z^{- 1} + 0.2 z^{- 2} \end{matrix}] \cdot \\ Δ y (k) = [\begin{matrix} 1 + 1.5 z^{- 1} & z^{- 1} \\ 0 & 1 + z^{- 1} \end{matrix}] Δ u (k - 1) (46) \end{array}$

控制器参数设定为:N=3, N_u=2, λ= 0.2, α= 0.5。目标函数y_r1 (k) , y_r2 (k) 是2个方波。

经推导得系统的回差矩阵行列式为

$\begin{array}{l} \det D (z^{- 1}) = \det [Ι + Q (z^{- 1}) S (z^{- 1})] = \\ n u m (z) / 128 d e n (z) (47) \end{array}$ $\begin{array}{l} \det D (z^{- 1}) = \det [Ι + Q (z^{- 1}) S (z^{- 1})] = \\ n u m (z) / 128 d e n (z) (47) \end{array}$

其中

$\begin{array}{l} n u m (z) = 5.192 z^{8} - 1.140 z^{7} - 1.139 z^{6} - \\ 1.004 z^{5} + 0.3230 z^{4} + 0.1272 z^{3} + \\ 0.04685 z^{2} - 0.01269 z + 0.0006923 (48) \\ d e n (z) = (0.04056 z^{6} - 0.02368 z^{5} - \\ 0.06297 z^{4} + 0.04127 z^{3} + 0.01562 z^{2} - \\ 0.01624 z + 0.0031) (z - 1)^{2} (49) \end{array}$ $\begin{array}{l} n u m (z) = 5.192 z^{8} - 1.140 z^{7} - 1.139 z^{6} - \\ 1.004 z^{5} + 0.3230 z^{4} + 0.1272 z^{3} + \\ 0.04685 z^{2} - 0.01269 z + 0.0006923 (48) \\ d e n (z) = (0.04056 z^{6} - 0.02368 z^{5} - \\ 0.06297 z^{4} + 0.04127 z^{3} + 0.01562 z^{2} - \\ 0.01624 z + 0.0031) (z - 1)^{2} (49) \end{array}$

由式 (45) 可知num (z) 为闭环特征多项式, 其根为闭环传递函数的极点, 定义为ρ_c。den (z) 则为开环特征多项式, 其根为开环传递函数的极点, 定义为ρ_o。求得闭环极点和开环极点如下:

$\begin{array}{l} ρ_{c} = 0.6155 + 0.1041 j, 0.6155 - 0.1041 j, \\ - 0.3471 + 0.4490 j, - 0.3471 - 0.4490 j, \\ - 0.01506 + 0.2639 j, - 0.01506 - 0.2639 j, \\ - 0.2175, - 0.06960; \\ ρ_{o} = - 1.076, - 0.7395, 1.087, 0.9999, 0.9999, \\ 0.5019, 0.4051 + 0.1081 j, 0.4051 - 0.1081 j 。 \end{array}$ $\begin{array}{l} ρ_{c} = 0.6155 + 0.1041 j, 0.6155 - 0.1041 j, \\ - 0.3471 + 0.4490 j, - 0.3471 - 0.4490 j, \\ - 0.01506 + 0.2639 j, - 0.01506 - 0.2639 j, \\ - 0.2175, - 0.06960; \\ ρ_{o} = - 1.076, - 0.7395, 1.087, 0.9999, 0.9999, \\ 0.5019, 0.4051 + 0.1081 j, 0.4051 - 0.1081 j 。 \end{array}$

可见, 闭环极点8个都在单位圆内, 满足定理1对于MIMO-GPC控制器闭环系统稳定的充分必要条件。

回差矩阵行列式奈奎斯特图如图3所示, 由图3可见该系统的回差矩阵D (z) 关于原点的周数为

《图3》

图3回差矩阵行列式的奈奎斯特图

Fig.3 Nquist diagram of return difference determinant

$e n c (D (z)) = - 2,$ $e n c (D (z)) = - 2,$

而系统的开环极点有2个在单位圆外, 满足定理2闭环系统稳定的充分必要条件。

图4为该系统的输出仿真曲线, 能很好的跟踪目标函数, 系统稳定收敛符合根据定理1和定理2的分析结果。

《图4》

图4仿真输出

Fig.4 Results of simulation

与单变量β-GPC^[4] 相似, 多变量GPC可使控制增量乘以β因子, 即在式 (21) 乘β, 仿真表明对系统的稳定性有明显影响。

$\begin{array}{l} Δ u (k) = β Ρ^{Τ} (W - F (z^{- 1}) y (k) - \\ z^{- 1} Η (z^{- 1}) Δ u (k)) (50) \end{array}$ $\begin{array}{l} Δ u (k) = β Ρ^{Τ} (W - F (z^{- 1}) y (k) - \\ z^{- 1} Η (z^{- 1}) Δ u (k)) (50) \end{array}$

式 (46) 所描述系统中, 其他控制参数不变, 取β=1.22, 代入式 (25) 至式 (27) , 计算闭环传递函数和回差矩阵D (z) , 得闭环特征多项式为

$\begin{array}{l} n u m (z) = 8.308 z^{8} - 5.816 z^{7} - 7.054 z^{6} - \\ 3.69 z^{5} + 1.749 z^{4} + 0.5688 z^{3} - \\ 0.809 z^{2} - 0.1383 z + 0.01649 (51) \end{array}$ $\begin{array}{l} n u m (z) = 8.308 z^{8} - 5.816 z^{7} - 7.054 z^{6} - \\ 3.69 z^{5} + 1.749 z^{4} + 0.5688 z^{3} - \\ 0.809 z^{2} - 0.1383 z + 0.01649 (51) \end{array}$

开环特征多项式为

$d e n (z) = (0.1622 z^{6} - 0.02991 z^{5} -$ $d e n (z) = (0.1622 z^{6} - 0.02991 z^{5} -$

$\begin{array}{l} 0.3444 z^{4} + 0.1440 z^{3} + 0.1425 z^{2} - \\ 0.1043 z + 0.01846) (z - 1)^{2} (52) \end{array}$ $\begin{array}{l} 0.3444 z^{4} + 0.1440 z^{3} + 0.1425 z^{2} - \\ 0.1043 z + 0.01846) (z - 1)^{2} (52) \end{array}$

由式 (51) 和式 (52) 可分别计算出闭环极点ρ_c和开环极点ρ_o:

$\begin{array}{l} ρ_{c} = 0.8072, - 1.042, 0.3874 + 0.3739 j, \\ 0.3874 - 0.3739 j, - 0.5357 + 0.3276 j, \\ - 0.5357 - 0.3276 j, - 0.2504, 0.08233 ； \\ ρ_{o} = - 1.313, - 0.9021, 1.088, 0.9999, 0.9999, \\ 0.5019, 0.4051 + 0.1081 j, 0.4051 - 0.1081 j 。 \end{array}$ $\begin{array}{l} ρ_{c} = 0.8072, - 1.042, 0.3874 + 0.3739 j, \\ 0.3874 - 0.3739 j, - 0.5357 + 0.3276 j, \\ - 0.5357 - 0.3276 j, - 0.2504, 0.08233 ； \\ ρ_{o} = - 1.313, - 0.9021, 1.088, 0.9999, 0.9999, \\ 0.5019, 0.4051 + 0.1081 j, 0.4051 - 0.1081 j 。 \end{array}$

并绘出回差矩阵行列式det D (z¹) 的奈奎斯特图如图5所示。

《图5》

图5β=1.22回差矩阵行列式的奈奎斯特图

Fig.5 β=1.22 Nquist diagram of return difference determinant

闭环极点ρ_c 有一个在单位圆外, 不满足定理1的系统稳定充要条件。开环极点 ρ_o有2个在单位圆外, 而奈奎斯特图表明周数

$e n c (D (z)) = - 1,$ $e n c (D (z)) = - 1,$

不满足定理2的系统稳定充要条件。系统的输出仿真曲线见图6。系统的输出仿真曲线是振荡发散。

《图6》

图6β=1.22系统仿真输出

Fig.6 β=1.22 results of simulation

《7 结论》

7 结论

笔者提出并证明基于频域的多变量广义预测控制 (MIMO-GPC) 稳定性的分析方法, 可利用Nyquist稳定性判据, 分析基于闭环特征多项式的MIMO-GPC的稳定性。仿真表明这些判据形象直观, 可作为MIMO-GPC控制器参数设计的重要依据。为多变量预测控制的应用提供了重要的设计方法。

展示更多