《1 低频振荡的机理与研究方法》

1 低频振荡的机理与研究方法

电力系统在小扰动的作用下，发电机的转子之间有时会发生相对摇摆，同时输电线路上的功率也发生相应振荡，影响功率的正常输送，这时如果系统缺乏必要的阻尼就会失去动态稳定，引起发电机转子之间的持续振荡，这种振荡的频率很低，一般在 0.2 ~ 2.5 Hz，故称为低频振荡。 20 世纪 50 年代低频振荡在国外电力系统就出现过，在我国，1979 年 4 月在广东到九龙的弱联络线上观察到低频振荡，此后在湖南电力系统、湖北电力系统都发生过低频振荡现象。

一般认为，产生低频振荡的物理本质是发电机轴作为一个刚体相互间的相对摇摆，当系统的阻尼力矩为负时，就会发生增幅性低频振荡。 近些年来，随着对电力系统稳定性研究的深入，发现除负阻尼引起低频振荡外还存在着非线性、混沌等一些非线性奇异现象。 它们的发生是由于系统自身的非线性引起的，表现为与通常的非线性不同的振荡现象。 20 世纪 80 年代中期，Abed 和 Varaiya 首次揭示了电力系统低频振荡中的非线性奇异现象，并指出这种现象是由 Hopf 分歧引起的[1]，而在此之前，文献[2]在研究位于芝加哥的 Commonwealth Edison 电力系统时已经发现该系统的振荡是发生在线性化模型靠近虚轴的地方，文章虽没有明确指出，却也强烈暗示振荡是由于分歧现象引起的。1993 年文献[3]又利用分歧理论揭示了准无穷大系统中，近似周期变化的小扰动下，振幅增长的振荡将中止。

对于电力系统低频振荡的研究，按采用的模型分主要有两大类：一是基于线性化动态方程分析的小扰动法；二是以非线性动态方程为基础的时域仿真法和分歧理论。 基于线性化动态方程分析的小扰动法（又称为特征分析法）是长期以来进行低频振荡研究的主要方法，按照这一理论，只要电力系统出现一对实部为正、虚部为 0.4 ~ 0.5 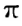 rad，与发电机的 δ 、ω 强相关的特征根，则系统就将出现增幅性低频振荡。 但实际上，由于电力系统是一个非线性系统，考虑到系统全部非线性特性、系统解的不唯一性、转折点和分歧点的存在，在虚轴附近电力系统也会出现奇异现象。 也就是说，在虚轴附近即使系统的全部特征根均位于虚轴左侧，系统非线性造成的分歧也可能造成增幅性低频振荡；反之，即使有一对共轭负根位于靠近虚轴右侧区域，分歧的出现也可能使系统由增幅性低频振荡转化为稳定的非线性振荡。 这种稳定与 Lyapunov 稳定性有着本质意义的区别，后者是对一个系统改变初始条件来研究系统的稳定性态，而考虑分歧存在的情况下，系统的拓扑结构已发生变化，反映出来的是系统状态的一种跳跃或突变。

《2 分歧理论》

2 分歧理论

分歧现象是普遍存在的，是非线性系统的重要特点之一，普遍存在于数学、物理学、化学、经济学、社会学、生态学等各个领域，像数学中的解不唯一、物理学中的相变、工程中的静力与动力失稳、经济学中的马太效应、电子学中的周期振荡、电力系统动态稳定分析等，都可以从分歧的角度去研究[4~6]。

《2.1 分歧的定义》

2.1 分歧的定义

动态系统从一种响应突然过渡到另一种响应时，连接两种响应的现象叫做分歧[5]。 对于分歧严格的具有普遍意义的定义如下：

定义：设 M 为 n 维流形，考虑定义在 M 上的系统

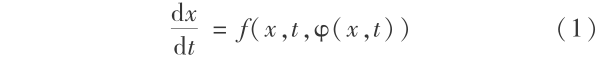
其中， φ∈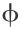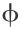，  是引入的类函数，在其上定义了量度。 它可以是向量，也可以是算子（对无限维）。 记式（ 1 ）的解空间为 X ＝｛x（ t ）；x（ t ） ∈Ｍ｝，引入等价类，即 X ＝ E1 ∪E2 ∪…，各个等价类是互不相交的（即 Ei ∩Ej ＝ Ф，i ≠ j 时））。

如果存在 φ 0（ x  ，t 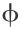）∈ ，对任意 ε ＞ 0 ，存在满足

｜φ1－φ0 ｜＜ ε 和 ｜φ2－φ0｜＜ ε

φ1 ， φ2 ∈ φ，使系统

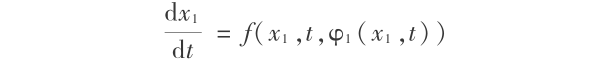
式（ 2 ）的解 x1 ( t ），x2（ t ）分别属于不同的等价类，则称 φ0（ x ，t ）为系统（ 1 ）的一个分歧点。

《2.2 Hopf 分歧》

2.2 Hopf 分歧

在系统（ 1 ）中，当 φ（ x ，t ）＝ μ 时，可以得到单参数系统：

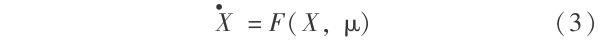
这里 X∈Rn 为状态变量，μ∈R 是系统参数（也称为控制参数）。

在平衡点处展开式（ 3 ）得：

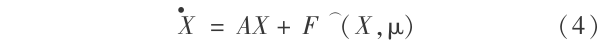
称满足 F（ X，μ ）＝ 0 的解 X（ 0，μ ）是系统（ 3 ）的平衡态解，它是式（ 1 ）所决定的一种最终状态。

分歧理论指出，当式( 4 )中矩阵 A 的特征值具有非零实部时，式( 3 )与式（ 4 ）在平衡点附近是拓扑等价的，奇异现象就发生在使 A ( μ )具有零实部特征值的点处。 如果 μ ＝ μc 时，A ( μ )有零特征值穿越虚轴，将出现静分叉现象，称为鞍点分歧；如果 μ = μc 时，A ( μ )有一对共轭复特征值穿越虚轴，就会出现由平衡态到周期解的分歧，称为 Hopf 分歧。

由 Hopf 分歧定理可知，当曲率系数 β2 ＞ 0 ，在临界点附近系统将由 Lyapunov 意义下的渐进稳定跃变为轨道不稳的非线性振荡，称为亚临界分歧；如果 β2 ＜ 0 ，在临界点附近系统将由 Lyapunov 意义下的不稳定跃变为轨道稳定的非线性振荡（等幅振荡），称为超临界分歧。 发生亚临界分歧时，如果横截条件 α’( μc ) ＞ 0 ，则分歧发生在临界点左侧，反之则发生在临界点右侧；而在超临界分歧发生时，如果横截条件 α’( μc ) ＞ 0 ，分歧发生在临界点右侧，反之则发生在临界点左侧[4]。

对于曲率系数 β2 的计算，当系统为二阶（ n ＝ 2 ），β2 的计算较为简单，文献[3]给出了 β2 的计算公式， 而在高维系统( n ＞ 2 )的分析中，需进行一个约化过程，即将高维非线性空间向低维流型化简，降维后的低维流型将保持其拓扑结构不变，即保留原来的全部非线性特征。 约化的方法有中心流型理论、Lyapunov - Schmit 方法等，其中用的最多的是中心流型理论[7]，文章中 β2 的计算即采用这一方法进行约化。

《3 单机无穷大系统算例》

3 单机无穷大系统算例

图 1 中，忽略线路电容和电阻，无穷大系统电压为 ＝ 1 ∠ 0 。 采用晶闸管快速励磁的电压自动调节系统传递函数  =  ，其中 Ke 和 Te 是励磁系统等值放大倍数和时间常数，Vt 是机端电压，描述系统的微分方程为[8]：

《图1》

图1 单机无穷大系统

Fig.1 Single－infinite power system

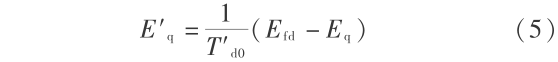
系统线性化后的微分方程表示为

系统参数 xd ＝ 0.982 ，x ′d ＝ 0.344 ，

xe = xt + x = 0.504

xdΣ = xqΣ = 1.486，x ′dΣ = 0.848 ，

T ′do = 5.0 ，M = 10 ，D = 0.75 ，Te = 0.4 ，δ = 49º

取放大倍数 Ke 作为系统控制参数 μ 。 下面用 Hopf 分歧理论分析系统的在临界点附近动态行为。

首先算得系统临界点为 μc = Ke = 39.410 86 ，此时系统特征根为｛0 ±j5.886 204 ， -1.462 736 ±j3.367 631 ｝， 按中心流形理论给出的方法，经计算得到曲率系数 β2 = 0.126 128 ，横截条件 α′( μ ) = 0.018 256，根据 Hopf 分歧理论，在临界点附近，系统发生了亚临界分歧，而且分歧发生在临界点左侧，于是得出这样的结论：由于发生了亚临界分歧，在 μ ＜ μc（ Ke ＜ Kec ）的邻域内，系统的动态行为出现了奇异，即特征值仍在虚轴左侧时，系统就开始不稳，出现增幅性振荡。 为了验证这一结论，可以利用数值积分（ step by step )的方法加以验证。

以输入机械功率的变化 ΔPｍ 作为扰动量，显然在平衡点 Pm = 1（即 ΔPm = 0 ）处，当 Ke ＜ Kec 时，系统特征根均位于 Ｓ 平面的左半平面，此时系统是稳定的，加入小扰动后，使系统过渡到所研究的平衡态 Pm = 1.05，此时对线性化前后的两组微分方程（式（ 5 ）和式（ 6 ））进行数值积分，得到的曲线如图 2 和图 3 所示。

《图2》

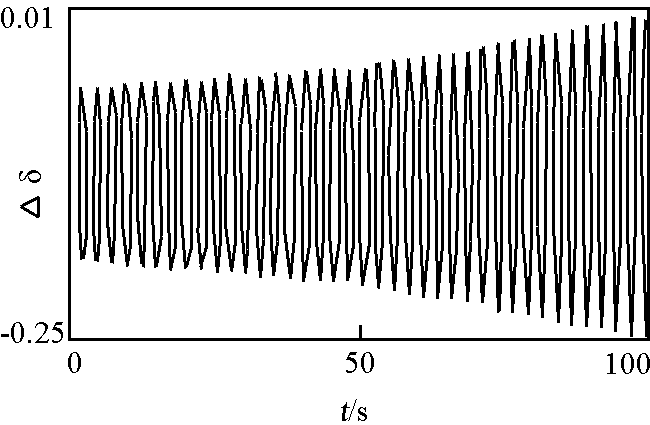
图2 Ke ＝ 39 时，方程 ( 5 ) 的解曲线

Fig.2 Solution curve of equation ( 5 ) when Ke ＝ 39

《图3》

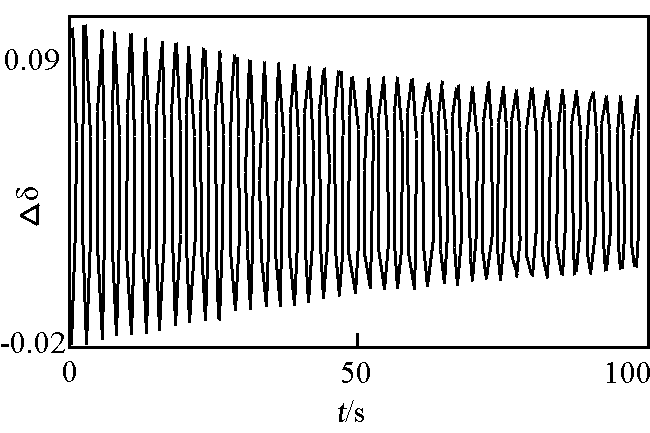
图3 Ke ＝ 39 时，方程 ( 6 ) 的解曲线

Fig.3 Solution curve of equation ( 6 ) when Ke ＝ 39

由图 2 和图 3 可以看出，加入小扰动后，在 Ke ＜ Kec 时，非线性系统就开始出现了增幅性低频振荡，而对应的线性化系统却是衰减的。

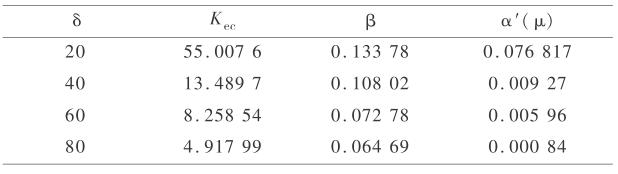
进一步分析可知，对所研究的系统，在改变运行方式的情况下，亚临界分歧的性质也不会改变（见表 1 ）。

《表1》

表1 以 Ke 作为控制参数，Te ＝ 0.01，其他参数不变，不同 δ（单位：度）时的计算结果

Table1 Te ＝ 0.01，control parameter is Ke ，other parameter is fixed，the calculating result when δ （ unit：degree ） is varied

《4 结语》

4 结语

以上分析可以看出，对所研究的系统，由于 Hopf 分歧现象，导致系统在临界点附近的动态行为出现奇异，而且在改变运行方式的情况下，亚临界分歧的性质也没有改变。 同时可以看出，系统在重负荷快速励磁的情况下，放大倍数的临界值减小，因此在小扰动作用下易发生增幅性低频振荡，而亚临界分歧的存在使得这种情况更加恶化。