用可压缩流涡方法模拟叶轮机动静叶的相互作用

摘要

本课题组发展了一种扰动涡方法，用以研究叶轮机内动、静叶相互作用^[1，2]。其优点是物理图画清楚，计算收敛快。它采用了一个重要假设：扰动胀量为零，从而大大简化了计算过程。文章的目的是研究此假设的影响，并取消此假设，使扰动涡方法建立在完全严格的数学基础上。由于取消了“扰动胀量为零的假设，需要耦合求解扰动质量方程、扰动涡量输运方程和扰动能量输运方程。这是文章与文献[1，2]的主要区别。

文献[1,2]对NASA67压气机第一级内由于动、静叶间的相互作用引起的非定常流动过程作了数值模拟，并与试验结果作了对比。文章也作了同样的算例，以研究扰动胀量为零的影响。数值模拟结果表明，在引入了扰动胀量后，用扰动涡方法模拟动静干涉仍保持较好的收敛性和收敛速度，且与试验的符合程度更好。文章强调指出，即使对于非定常可压流，为满足无渗透边界条件所需的运动分量也是用椭圆类的拉普拉斯方程描述，而不是用双曲类的方程描述。“扰动胀童为零”不能等同于扰动运动为不可压。

正文

《引言》

引言

真实流体的流动从严格意义上说都是随时间变化的, 即都是非定常流。由于动、静叶片排间的相对运动和每个叶片排流场的周向非均匀性, 使得叶轮机内部的流动本质上是非定常的。本文就是研究这一类非定常流动, 而不涉及与流动失稳相关的非定常性。

过去叶轮机内部流场的计算主要基于这样一个近似:对于转子相对坐标系, 绕转子叶片排的流动是定常的;对于静子坐标系, 绕静子叶片排的流动是定常的。前已说明, 这个假设是不真实的。已有的研究结果表明, 叶轮机内动、静叶非定常干扰影响着叶轮机的叶片载荷、级效率、传热特性、喘振裕度和噪声特性等各方面的性能。因此研究动、静叶排相互作用, 了解非定常性对于平均定常性能的影响, 弄清其影响机理, 对于进一步提高叶轮机械的性能是十分必要的

随着计算机水平和试验测量技术的提高, 越来越多的学者开始尝试采用不同的数值模拟方法和试验手段来研究叶轮机内非定常流动现象, 并取得了可喜的成果^[3～5]。

本课题组发展了一种扰动涡方法, 用以研究叶轮机内动、静叶相互作用^[1,2]。其基本思想是以全三维、相对于动叶和静叶的定常流动的数值解为基础, 采用瞬时量分解的方法, 求出非定常扰动的初始解, 然后用涡动力学方法及拉格朗日方式追踪扰动涡团运动的时间历程, 从而描述叶轮机内动、静叶相互作用的非定常流动过程。文献[1]的数值模拟结果与实验结果吻合得较好, 这表明用扰动涡方法来研究叶轮机动、静叶相互作用是可行的, 且计算收敛快。该文采用了一个重要假设, 即扰动胀量为零, 从而大大简化了计算过程。本文的目的是研究此假设的影响, 并取消此假设, 使这种扰动涡方法建立在完全严格的数学物理基础上。由于取消了扰动胀量为零的假设需要耦合求解扰动质量方程、扰动涡量输运方程和扰动能量输运方程, 这是本文与文献[1]的主要区别。结果表明, 在引入了扰动胀量后, 用扰动涡方法模拟动静干涉仍保持较好的收敛性和收敛速度, 且与试验的符合程度更好。除此之外, 本文还研究了与“扰动胀量不为零”的一些理论问题。本文强调指出, 即使对于非定常可压流, 为满足无渗透边界条件所需的运动分量也是用椭圆类的拉普拉斯方程描述, 而不是用双曲类的方程描述。本文还指出, “扰动胀量为零”不能等同于扰动运动为不可压。

就作者所知, 将涡方法用于动静叶相互作用问题始于本课题组^[1], 而将涡方法用于可压流问题资料也很少。

《1 扰动涡方法》

1 扰动涡方法

《1.1 控制方程组》

1.1 控制方程组

从流体力学基本方程组出发, 将瞬时参数 (以q表示) 分成平均参数和扰动参数两部分, 即

\(q=\bar{q}+q_{\text {, 其中 }}^{\prime}\)
\(\bar{q}=\frac{1}{T} \int_{0}^{T} q \mathrm{~d} t\), T是考虑了动、静叶相互作用干涉后的周期 (或其倍数) , 使
\(\bar{q}\)不再是t的函数, 则由定义可知:
\(\int_{0}^{T} q^{\prime} \mathrm{d} t=0\), 以此为出发点推导了诸扰动方程^[6]。

1.1.1 扰动质量方程

由流体质量方程并利用分解瞬时量的方法可以推出扰动质量方程

\(\begin{array}{l} \frac{\mathrm{d} \rho^{\prime}}{\mathrm{d} t}=-\left(\boldsymbol{u}^{\prime} \cdot \nabla\right) \rho+\overline{\left(\boldsymbol{u}^{\prime} \cdot \nabla\right) \rho}-\\ \rho^{\prime} \overline{H_{m}}-\rho H_{m}{ }^{\prime}-\rho^{\prime} H_{m}{ }^{\prime}+\overline{\rho^{\prime} H_{m}}, \end{array}\) （1）

其中平均胀量

\(\overline{H_{m}}=\nabla \cdot \boldsymbol{U}\), 扰动胀量
\(H_{m}{ }^{\prime}=\nabla \cdot \boldsymbol{u}^{\prime}\)。

1.1.2 扰动涡量输运方程

粘性可压流, 彻体力有势, 正压流体的涡动力学方程^[7]为

\(\begin{array}{c} \frac{\partial \omega}{\partial t}+(\boldsymbol{u} \cdot \nabla) \omega=(\omega \cdot \nabla) \boldsymbol{u}-\omega(\nabla \cdot \boldsymbol{u})+ \\ \nu \nabla^{2} \omega+\nabla \nu \times\left[\nabla^{2} \boldsymbol{u}+\frac{1}{3} \nabla(\nabla \cdot \boldsymbol{u})\right] \end{array}\) （2）

同样, 利用分解瞬时量的方法可得全三维扰动涡量输运方程

\(\begin{array}{l} \frac{\mathrm{d} \omega^{\prime}}{\mathrm{d} t}=-\left(\boldsymbol{u}^{\prime} \circ \nabla\right) \Omega+\overline{\left(\boldsymbol{u}^{\prime} \circ \nabla\right) \omega}+(\Omega \circ \nabla) \boldsymbol{u}^{\prime}+\\ \left(\omega^{\prime} \circ \nabla\right) \boldsymbol{U}+\left(\omega^{\prime} \circ \nabla\right) \boldsymbol{u}^{\prime}-\overline{\left(\omega^{\prime} \circ \nabla\right) \boldsymbol{u}}-\omega^{\prime}(\nabla \circ \boldsymbol{U})\\ -\Omega\left(\nabla \cdot \boldsymbol{u}^{\prime}\right)-\omega^{\prime}\left(\nabla \cdot \boldsymbol{u}^{\prime}\right) \overline{+\omega^{\prime}\left(\nabla \cdot \boldsymbol{u}^{\prime}\right)}+\bar{\nu} \nabla^{2} \omega^{\prime}\\ +\nu^{\prime} \nabla^{2} \Omega+\nu^{\prime} \nabla^{2} \omega^{\prime}-\overline{\nu^{\prime} \nabla^{2} \omega^{\prime}}+\nabla \nu \times \nabla^{2} \boldsymbol{u}^{\prime}+\underline{\nabla \nu^{\prime}}\\ \times \nabla^{2} \boldsymbol{U}+\nabla \nu^{\prime} \times \nabla^{2} \boldsymbol{u}^{\prime}-\overline{\nabla \nu^{\prime} \times \nabla^{2} \boldsymbol{u}^{\prime}}+\frac{1}{3} \nabla_{\nu} \times\\ \nabla\left(\nabla \cdot \boldsymbol{u}^{\prime}\right)+\frac{1}{3} \nabla \nu^{\prime} \times \nabla(\nabla \cdot \boldsymbol{U})+\frac{1}{3} \nabla \nu^{\prime} \times \nabla(\nabla\\ \left.\cdot \boldsymbol{u}^{\prime}\right)-\frac{1}{3} \nabla \nu^{\prime} \times \nabla\left(\nabla \cdot \boldsymbol{u}^{\prime}\right) \end{array}\) (3)

式中

\(\frac{\mathrm{d} \omega^{\prime}}{\mathrm{d} t}=\frac{\partial \omega^{\prime}}{\partial t}+\left(\boldsymbol{U}^{\circ} \nabla\right) \omega^{\prime}+\left(\boldsymbol{u}^{\prime} \circ \nabla\right) \omega^{\prime} .\), 带双划线的部分是取消“扰动胀量为零”的假设后引入的项, 可见由此带来的计算量和复杂性都是很大的。

1.1.3 扰动总能量输运方程

用同样方法可导出扰动总能量输运方程, 由于公式很长, 这里从略, 可参看文献[6]。

1.1.4 关于“扰动胀量为零”假设的讨论

在文献[1]中引进了“扰动胀量为零” (即·u′=0) 的假设, 并近似认为这一假设包含了密度的扰动量ρ′为零及扰动运动不可压, 因而只需单独求解扰动涡量的输运方程, 而没有把质量方程、动量方程和能量方程耦合求解, 这样可以使计算得到很大的简化。虽然文献[1]得到了较为合理的数值模拟结果, 但这样处理是不严格的。

全速度的胀量为零的确等价于流动不可压, 但扰动胀量为零并不等价于扰动运动不可压。因为根据扰动质量方程 (1) 式, 设

, 则有

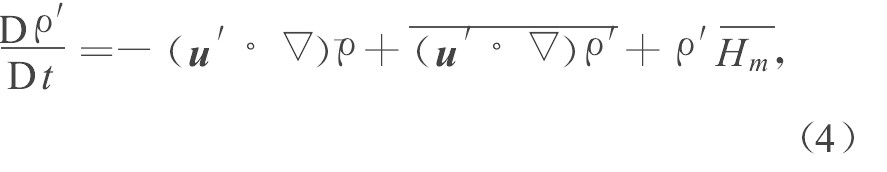
可见

不等价于

。因此“扰动胀量为零”不能等同于扰动运动不可压。所以, 即使是假设“扰动胀量为零”, 也应耦合求解诸扰动方程。

《1.2 定解条件》

1.2 定解条件

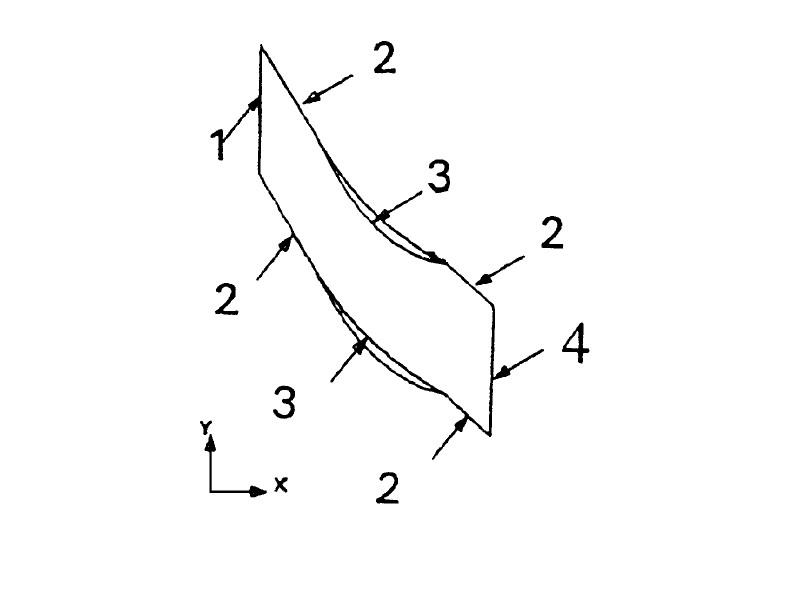
定解条件的取法与文献[1]相同。单排叶片物理域二维示意图如图1所示, 此物理域处于相邻叶片吸力面与压力面之间, 并分别向叶片上游和下游延伸。因此存在四种类型的边界条件:1进口边界条件;2几何周期边界上的相漂移周期性边界条件 (当动、静叶的栅距不等时) ;3固壁边界条件;4出口边界条件。

1.2.1 初始条件

本文取全三维、分别相对于动叶和静叶为定常流动的数值解作为物理域内各对应点上流动参数的时间平均值。而物理域内各对应点上流动参数的扰动量初始值的给法以单级轴流压气机为例来说明。如图2所示, 在初始时刻t₀, 由于尚不知道动叶在静叶通道内所引起的扰动量的分布所以先不考虑静叶通道内动叶的影响而仅计及动叶在静叶上游边界上的影响。静叶的定常解Q_S (x, y) 和上游动叶相对运动的定常解Q_R (x, v_rt) 是已知的, 这里x, y是流面上任意点的位置坐标, v_r是当地动叶的移动速度。此时静叶通道内非定常初始条件可表示成

《图1》

图1 平面叶栅通道边界条件示意图

Fig.1 Boundary conditions of a linear cascade

其中, Q_{R (axi)} (x) 是Q_R (x, y) 在轴向位置x处的周向平均值, x_inlet是静叶通道进口截面的轴向坐标。

《图2》

图2 单级轴流压气机叶栅通道示意图

Fig.2 Cascade flow passage for single stage axial flow compressor

1.2.2 边界条件

1) 固壁边界条件。u′·n=0, u′·τ=0, (6) n是固壁法向单位向量, τ是固壁切向单位向量。

2) 进口边界条件。图2中动、静叶的相对位置随动叶的运动而变化。从某一时刻t₀起, 经过Δt时间段, 动叶将运动到一新位置。按照扰动量初始条件的取法可求出新时刻进口边界上的扰动量, 其表达式为

这里t=t₀+kΔt, (1≤k≤N) , Δt=T/N。T是静叶进口边界上某一点扫过一个动叶栅距所用的时间, 即ΔT=P_r/v_r, P_r是动叶栅距。N是将时间T等分的个数。

3) 相漂移周期性边界条件。当动、静叶的栅距比不是整数时, 边界条件将不再是周期性的了。如图2, 研究一典型单级轴流压气机的中间流面, 其中动叶栅距大于静叶栅距。某一时刻, 静叶排的下边界与上游动叶排的下边界对齐。经过一段时间, 静叶排的上边界与上游动叶排的上边界对齐。所经历的这段时间正好是动、静叶的栅距之差与动叶当地周向速度之比。因此计算域边界条件满足的是“相漂移周期性边界条件”

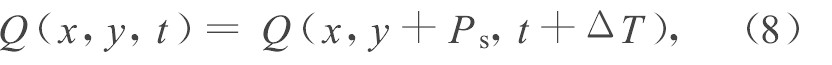
其中时间差ΔT= (P_r-P_s) /v_r, P_r、P_s分别是动叶和静叶的栅距, v_r为动叶的当地周向速度。

《1.3 扰动量的计算》

1.3 扰动量的计算

1.3.1 扰动涡团的扰动密度和扰动能量

由 (1) 式和扰动能量方程, 扰动涡团在新时刻的扰动密度和扰动能量可根据下式求出:

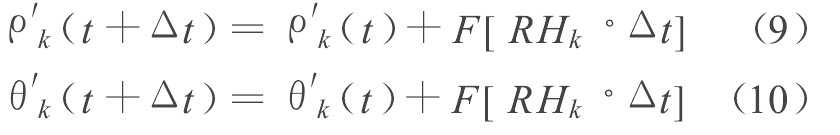
式中RH代表 (1) 式和扰动能量方程的右手项。1.3.2扰动涡团的扰动环量根据Chorin的方法 (Vortex Blob Method) ^[8], 将扰动涡量的输运方程 (3) 分解为粘性扩散方程 (11A) 和对流方程 (11B) , 而分别求解。

为便于求解由扰动涡量诱导出的扰动速度分量本文实际求解的是扰动环量的输运方程

在二维条件下, 计算中所引入的扰动涡元数目要比三维情况下少得多。当计算收敛后, 计算域内不同周期对应于同一动、静叶相对位置的流体涡团的平均运动轨迹会完全相同。因此, 当涡元数目不够多时, 如果用随机走步方法来模拟扰动涡量的扩散过程, 会使计算精度下降。若采用确定性涡方法可以有效地解决这一问题。本文采用形函数求导法来处理, 即

则涡量的Laplace算子可写成

于是扰动涡量的扩散方程 (11A) 式对涡元加以离散后得到

《1.4 扰动速度各分量的表达式》

1.4 扰动速度各分量的表达式

扰动速度可分解为u′=u′_in+u′_e+u′_p (15) 其中u′_in为扰动涡量诱导速度, u′_e为扰动胀量诱导速度, u′_p是为满足壁面无穿透条件而引入的扰动势速度。下面是二维扰动速度各分量的求解公式 (详细推导参见文献[6]) 。

1) u′_e的分速度离散形式为

2) u′_in的分速度离散形式为

3) 扰动势速度u′_p由扰动胀量诱导速度u′_e和扰动涡量诱导速度u′_in的引入过程可知, 若已知区域内所有点上的扰动涡量ω′和扰动胀量Hm′, 则应有

可见存在一个速度势使得

即此位势函数满足拉普拉斯方程。应该指出, 式 (20) 的存在并不以扰动分量是否可压为前提, 而且对于非定常流, 此式仍然成立。初看起来此结论似不合理, 因为对于非定常流动应由双曲类方程描述, 而不应由椭圆类方程描述。实际上此关系的正确性是由速度分解关系 (15) 决定的, 而 (15) 式是一个运动学关系, 它的成立并不依赖于动力学过程。 (16) 和 (17) 式可以充分反映动态过程的变化。Batchelor^[9]对此作过这样的解释:“控制速度分布从一个瞬间到另一个瞬间变化的动力学方程通常是非线性的, 但在无旋无胀量流的特殊情况下, 对速度分布的约束是如此之强, 以至要求其满足简单的线性方程, 即 (20) 式, 而与瞬间的变化无关。”

式 (16) 和式 (17) 中k_e和k_in是奇异核函数, 当两个点涡无限接近时会诱导出无穷大速度, 导致涡元的杂乱无章的运动。为了抑制涡元的混乱运动, 要引入非奇异核函数:选取光滑函数

, 对于圆形涡团而言, σ相当于涡团半径, f (r) 为核函数, f_σ (r) 是个迅速衰减的函数, 涡量主要集中在r<σ的范围内。本文取二阶高斯核:

。由此, 非奇异核函数公式是

把式 (21) 代入式 (16) 和式 (17) 结合有:

扰动胀量诱导速度公式离散形式

扰动涡量诱导速度公式离散形式

《1.5 壁面上扰动涡的生成》

1.5 壁面上扰动涡的生成

新一时刻流场内扰动涡量场和扰动胀量场产生的诱导速度加上扰动势速度而合成的速度场, 虽然满足涡量动力学方程和固壁无穿透条件, 但是一般仍然会在固壁上产生滑移速度, 对于粘性流动来说这个滑移速度实际上是不存在的, 必然有某种机制将它抵消掉。本文采用Chorin^[8]的新生涡方法来满足固壁无滑移条件。

《1.6 新时刻扰动涡元的位置》

1.6 新时刻扰动涡元的位置

本文利用格子涡 (Vortex in Cell VIC) 方法的思想来计算涡元中心的速度。根据已求出的网格节点上的合速度, 用面积加权法内插求出各涡元中心的速度^[6]:

其中u_kk, v_kk分别是网格节点处的速度分量, u_n, v_n是涡元中心处的速度分量, S_kk是各微元面面积, S为S₁, S₂, S₃, S₄之和。由此可算出各涡元在下一时刻的所在位置:

《2 算例与结果分析》

2 算例与结果分析

《2.1 方法校验》

2.1 方法校验

为检验方法的有效性, 需要把数值模拟结果与试验数据进行对照。首先对NASA67压气机展中流面处的非定常流动过程作了数值模拟, 将计算得到的扰动速度关联项与近似位置处的试验数据进行了对比 (如图3, 图4和图5) 。图中提供了四个计算站的对比结果, 即-4.98%, 4.45%, 50.7%和100%轴向弦长处扰动关联项

沿栅距向的分布。从图中可见, 在计算域的大部分区间里, 计算结果和试验数据的变化趋势是一致的, 但在靠近叶栅吸力面处 (即图中横坐标100%附近) 计算结果和试验数据的量差较大, 以

为显著。差别的来源是多方面的, 既有方法本身的数值误差, 同时也不能排除试验测量误差。对照试验数据和模拟结果, 笔者认为本文的方法及程序是可信和有效的。

《图3》

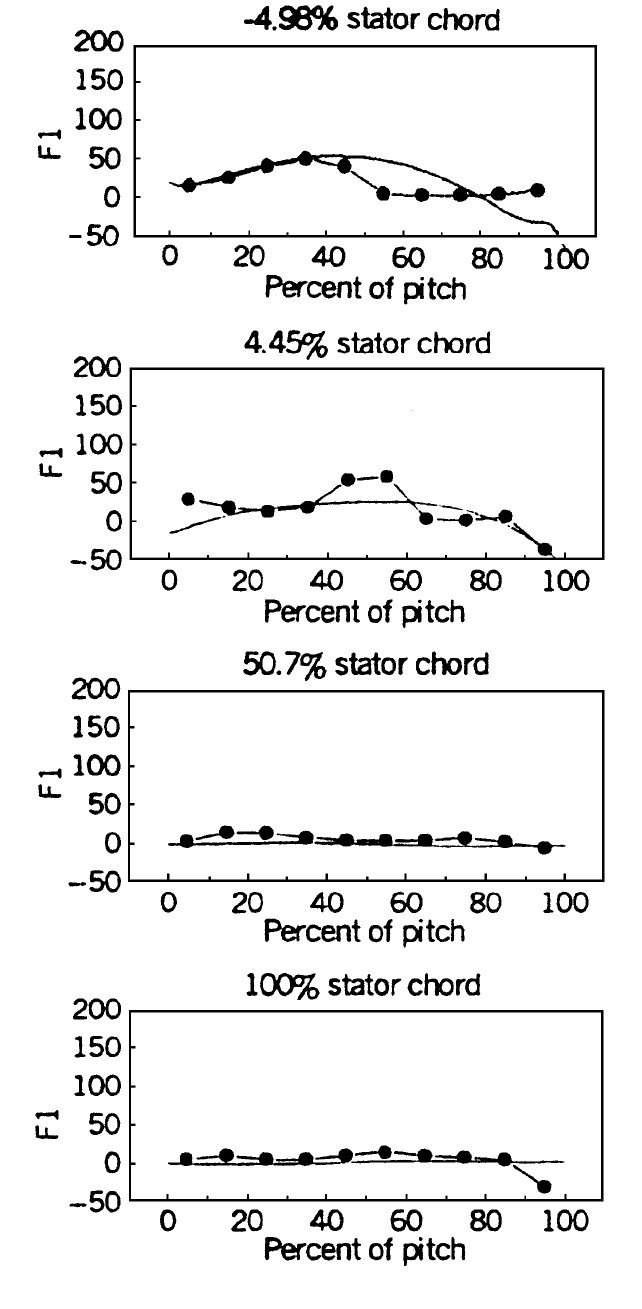
图3 50%流面上扰动关联项\(\overline{u^{\prime} v^{\prime}}\)分布（m²/s²）

Fig. 3 Circumferential distributton of \(\overline{u^{\prime} v^{\prime}}\) at 50% span （m²/s²）

《图4》

《图5》

本文与文献[2]采用的是同一个算例。图6, 图7和图8给出了文献[2]计算得到的扰动速度关联项与近似位置处的试验数据的对比图。图中的四个计算站分别位于-5%, 5%, 50%和100%轴向弦长处。对比图3～图8, 无论本文的计算结果还是文献[2]的计算结果, 总的来说变化趋势与对应的试验结果均保持一致。但我们注意到, 试验结果表明考查的三个速度关联项在轴向弦长50%处以后均接近于零。从图6, 图7和图8中可以看出, 文献[2]的计算结果与试验结果在轴向弦长50%处以后还是有明显的差别, 但此时本文的计算结果可以与试验结果较好地吻合。因此, 为使计算方法更加完善和严格, 并得到更好的数值结果, 在扰动涡方法中计入扰动胀量, 并耦合求解诸扰动方程是有必要的。

《2.2 算例介绍》

2.2 算例介绍

为便于比较, 采用了与文献[2]相同的算例, 且网点数和时间步长也相同, 即动叶区和静叶区的计算网格分别取80×33和40×33, 时间步长按每21个时间步走完1个动叶扫过周期来确定。用本文开发的计算程序计算5个动叶扫过周期需耗时9h, 而用文献[2]开发的程序只需4 h (所用计算机为PⅡ233) 。

《图6》

《图7》

《图8》

《2.3 收敛性分析》

2.3 收敛性分析

图9给出了静叶压力面观察点 (靠近叶片前缘) 处马赫数在计算过程中的变化曲线。可见, 观察点处的马赫数随动叶的扫过作周期性的脉动。三个动叶扫过周期后, 观察点处的马赫数脉动就达到了较好的重复。

《图9》

图9 观察点处马赫数变化曲线

Fig.9 Unsteady Mach number at the monitoring point

《图10》

图1 0 计算域内扰动涡团数目随时间的变化

Fig.10 The amount of disturbance vortex evolution

图10给出了5个动叶扫过周期内计算域中扰动涡团数目的变化。同样, 3个动叶扫过周期后, 计算域内扰动涡团数目也达到了较好的重复。在第四周期时, 最大相对扰动涡团数

, 仅为0.001 7, 密度的网格结点平均相对误差最大为0.003 8, 马赫数的网格结点平均相对误差最大为0.002 4。

综上, 扰动涡方法在经过3个动叶扫过周期后就达到了收敛状态。与文献[1]比较可见, 计入了扰动运动的压缩性后, 仍能得到好的收敛性。

《2.4 计算结果与分析》

2.4 计算结果与分析

1) 正如第1.1.4节所讲的那样, 即使假设“扰动胀量为零”, 扰动密度也不为零, 因而必需耦合求解诸扰动方程。图11a就是这样得出的。它给出了叶栅通道内不同轴向计算站沿栅距向的扰动密度ρ′的强度分布曲线。可以看出, 在·u′=0的假设下扰动密度不光有变化, 而且扰动密度强度变化剧烈的地方, 也正是扰动速度强度取值大的地方。本算例扰动密度强度的最大值甚至达到约0.15。可见, 把“扰动胀量为零”等同于扰动运动不可压会带来一定的误差。

2) 取消“扰动胀量为零”假设后的扰动密度场。图11b给出了叶栅通道内不同轴向计算站沿栅距向的扰动密度ρ′的强度分布曲线。可以看出, 此时的扰动密度强度分布与在·u′=0的假设下的分布情况大体相同, 但数值不同。

《3 结论》

3 结论

1) 从粘性可压缩流体的N S方程出发, 经过严格的推导, 得出了在扰动胀量不为零的条件下, 全三维扰动涡量输运方程、扰动质量方程及扰动能量输运方程。

2) 由扰动质量方程可见, “扰动胀量为零”并不能等同于扰动运动不可压。所以, 即使假设“扰动胀量为零”, 也必需耦合求解诸扰动方程。

3) 由于取消了“扰动胀量为零”的假设, 扰动胀量的诱导速度将不为零。本文推出了扰动胀量与其诱导速度之间的关系式, 并得到了其非奇异化的二维离散表达式。

4) 扰动胀量诱导速度和扰动涡量诱导速度在壁面一般不能满足固壁无穿透条件, 为了满足此条件, 须叠加一个速度。本文强调指出这个叠加速度在扰动运动可压的条件下, 仍可由满足拉普拉斯方程的势函数表示。即使在可压、非定常的扰动运动中, 此边界条件仍由椭圆型方程表示而不是由含时间变量的抛物或双曲方程表示。

5) 与试验结果对照表明, 在大部分区域内, 模拟结果能较好地和试验数据相吻合, 且略优于假设扰动胀量为零得到的结果。所以, 本文的涡方法程序是可信的。

6) 数值模拟结果表明, 在引入了扰动胀量后用扰动涡方法模拟动静叶干涉仍保持较好的收敛和收敛速度。可以从计算结果中观察到许多非定常流动现象。

《图11》

展示更多