《1 引言》
1 引言
海洋波浪与振荡系统如船舶、海洋平台和波能转换装置的相互作用是海洋工程中的研究课题之一。波浪与振荡系统的相互作用一直受到设计者极大的关注, 精确计算波浪作用在振荡系统上的力对振荡系统的设计极为重要[1 ,2 ]
海底地形复杂, 波在传播过程中会遇到障碍物而改变传播方向, 产生绕射, 这种绕射会对上面的浮体运动产生作用, 浮体运动又反过来影响波的传播, 波与浮体之间的相互作用变得复杂。对这种条件下浮体的辐射和散射问题一般采用数值方法, 但数值方法在计算精度、计算效率以及程序实现方面都较复杂。为了简化计算而又能研究障碍物对浮体运动的一般性影响, 把障碍物简化为圆柱形, 采用解析方法研究这种条件下浮体的辐射和散射问题。尽管这种简化是一种理想化的情况, 但其结果可以近似地应用于许多有意义的实际场所, 有助于检验数值方法的正确性, 有助于进一步研究更复杂的情形。
Miles等人[3 ] [4 ] [5 ] [6 ] [7 ]
显然, 障碍物的存在, 尤其是其半径不同于浮体的半径时, 浮体的辐射和散射问题要比平底单浮体的辐射和散射问题复杂。在流体不可压缩、流动无旋、小振幅波的条件下, 作者采用特征函数展开法对处在同轴、半径大障碍物地形条件上的浮体的散射及辐射问题进行了研究, 推导出水动力系数表达式和激励力表达式, 把相应的水动力系数同同轴、同半径障碍物地形条件上的单浮体系数相比, 同时也比较了计算激励力的两种方法, 得到一致的结果。最后讨论了障碍物对浮体运动特有的影响, 得到了一些有意义的结果。
《2 问题描述》
2 问题描述
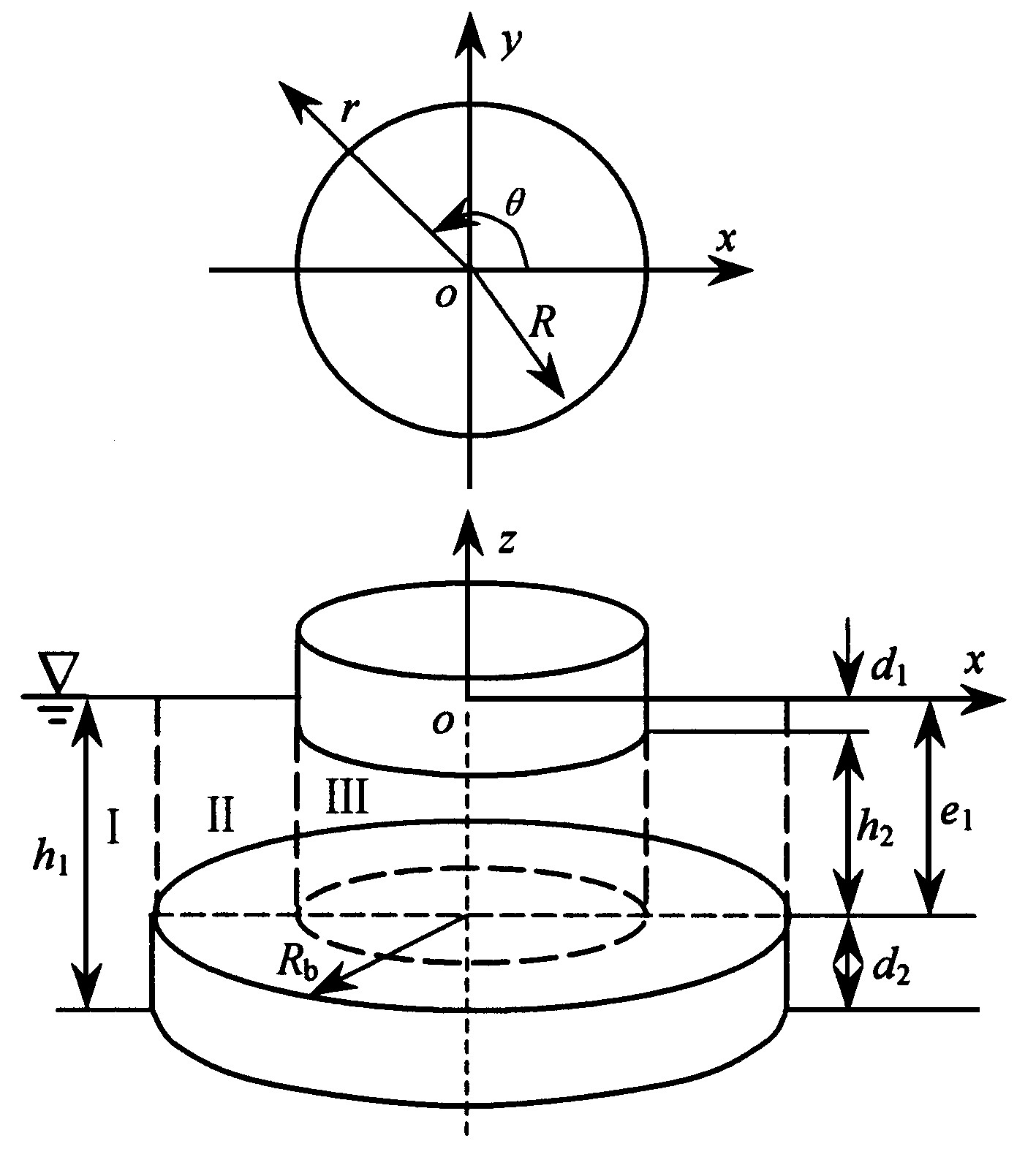
一个圆柱形浮体B, 其半径为R , 被置于等深度无旋、不可压缩的流体中, 其占据的空间为r ≤R , 0≤θ ≤2π, -d 1 ≤z ≤0, 其正下方有一同轴但半径大的圆柱体障碍物, 其半径为R b (R b ≥R ) , 它占据的空间为r ≤R b , 0≤θ ≤2π, -h 1 ≤z ≤-e 1 , 如图1所示。在线性入射波作用下, 浮体B作微摇荡运动。由于流体不可压缩, 流动无旋, 浮体仅在做微幅运动, 而且是柱对称问题, 所以流体的运动状态采用柱坐标下速度势表达式Φ (r , θ , z , t ) =ϕ (r , θ , z ) e -iwt 描述, ϕ (r , θ , z ) 为空间速度式。速度势Φ 满足拉普拉斯方程, 就得
∂ 2 ϕ ∂ z 2 + 1 r 2 ∂ 2 ϕ ∂ θ 2 + 1 r ∂ ∂ r ( r ∂ ϕ ∂ r ) = 0 , ( 1 ) ∂ 2 ϕ ∂ z 2 + 1 r 2 ∂ 2 ϕ ∂ θ 2 + 1 r ∂ ∂ r ( r ∂ ϕ ∂ r ) = 0 , ( 1 )
《图1》
图1 波能装置示意图
Fig.1 Sketch of the wave power device
ϕ又可分解为散射势ϕs 和由于物体运动产生的辐射势ϕr , 而散射势ϕs 又可分为波浪入射势ϕi 和由于物体存在且不动时引起的绕射势ϕd 。考虑单位振幅线性入射平面波作用, ϕi 为已知, 在柱坐标下, 其表达式[3 ]
ϕ i = − i g ω c o s h k ( z + h 1 ) c o s h k h 1 ⋅ ∑ m = 0 ∞ μ m J m ( k r ) cos m θ 。 ( 2 ) ϕ i = - i g ω c o s h k ( z + h 1 ) c o s h k h 1 ⋅ ∑ m = 0 ∞ μ m J m ( k r ) cos m θ 。 ( 2 )
μ m = { 2 i m 1 m > 0 m = 0 ; μ m = { 2 i m 1 m > 0 m = 0 ;
i = − 1 − − − √ i = - 1 ω 为波浪圆频率;k 为波数, 由色散关系k tanh (kh 1 ) =ω 2 /g 确定。在三维柱形地形条件下, ϕd 和ϕr 及其所推导的其它物理量是求解的重点。
《3 辐射速度势》
3 辐射速度势
《3.1辐射速度势问题》
3.1辐射速度势问题
在线性入射波作用下, 适当选取坐标系的取向可使浮体简单地分解为垂荡、纵荡 (或横荡) 、纵摇 (或横摇) 3种模态运动, 分别用l =1, 2, 3区分, 其运动的振幅为A l rΦ r 可表示为
Φ r = ∑ l = 1 3 Φ l r = ∑ l = 1 3 R e [ ϕ l r ( r , θ , z ) exp ( − i ω t ) ] = ∑ l = 1 3 R e [ − i ω A l r ψ l r ( r , θ , z ) exp ( − i ω t ) ] = ∑ l = 1 3 R e { − i ω [ A l r φ l r ( r , z ) cos ( 1 − δ 1 l ) θ ] ⋅ exp ( − i ω t ) } , ( 3 ) Φ r = ∑ l = 1 3 Φ l r = ∑ l = 1 3 R e [ ϕ l r ( r , θ , z ) exp ( - i ω t ) ] = ∑ l = 1 3 R e [ - i ω A l r ψ l r ( r , θ , z ) exp ( - i ω t ) ] = ∑ l = 1 3 R e { - i ω [ A l r φ l r ( r , z ) cos ( 1 - δ 1 l ) θ ] ⋅ exp ( - i ω t ) } , ( 3 )
式中ψ 和φ 为空间速度势, t 为时间。显然式中设定了如下关系
ψ l r ( r , θ , z ) = φ l r ( r , z ) cos ( 1 − δ 1 l ) θ , ( 4 ) ψ l r ( r , θ , z ) = φ l r ( r , z ) cos ( 1 - δ 1 l ) θ , ( 4 )
δ k l = { 1 k = l 0 k ≠ l 。 δ k l = { 1 k = l 0 k ≠ l 。
将式 (4) 代入拉普拉斯方程及相应的边界条件, 可得空间速度势φ l r
∂ 2 φ l r ∂ z 2 + 1 r ∂ ∂ r ( r ∂ φ l r ∂ r ) − ( 1 − δ 1 l ) 2 φ l r r 2 = 0 ∂ 2 φ l r ∂ z 2 + 1 r ∂ ∂ r ( r ∂ φ l r ∂ r ) - ( 1 - δ 1 l ) 2 φ l r r 2 = 0
∂ φ l r ∂ z − ω 2 g φ l r = 0 ‚ ( z = 0 , r ≥ R ) ( 6 ) ∂ φ l r ∂ z - ω 2 g φ l r = 0 ‚ ( z = 0 , r ≥ R ) ( 6 )
∂ φ l r ∂ z = 0 ‚ ( z = − h 1 , r ≥ R b ∂ φ l r ∂ z = 0 ‚ ( z = - h 1 , r ≥ R b 1 , r≤Rb
∂ φ l r ∂ r = 0 ‚ ( − h 1 < z < − e 1 , r = R b ) ( 8 ) ∂ φ l r ∂ r = 0 ‚ ( - h 1 < z < - e 1 , r = R b ) ( 8 )
∂ φ l r ∂ z = δ 1 l − r δ 3 l ‚ ( z = − d 1 , r < R ) ( 9 ) ∂ φ l r ∂ z = δ 1 l - r δ 3 l ‚ ( z = - d 1 , r < R ) ( 9 )
∂ φ l r ∂ r = δ 2 l + ( z − z c ) δ 3 l ∂ φ l r ∂ r = δ 2 l + ( z - z c ) δ 3 l
( − d 1 < z < 0 , r = R ) lim r → ∞ r √ ( ∂ φ l ∂ r − i k φ l r ) = 0 。 ( 1 1 ) ( - d 1 < z < 0 , r = R ) lim r → ∞ r ( ∂ φ l ∂ r - i k φ l r ) = 0 。 ( 1 1 )
注意:在式 (9) 和式 (10) 中, 假定纵摇支点坐标取为 (x c , y c , z c ) = (0, 0, z c ) 。
《2.2问题的求解》
2.2问题的求解
采用特征函数展开法求解上面的定解问题。首先将流体计算域划分成I、Ⅱ和Ⅲ 3个子域, 如图1所示。这3个子域的辐射速度势分别记为φ l r1φ l r2φ l r3r =R b 和r =R 外的所有边界条件) 。然后通过在r =R b 和r =R 处给出的压力和法向速度连续性条件来确定级数中的系数。
φ l r 1 = ∑ n = 1 ∝ A l n cos [ λ n ( z + h 1 ) ] R ( 1 − δ 1 l ) ( λ n r ) R ( 1 − δ 1 l ) ( λ n R b ) ‚ ( 1 2 ) φ l r 2 = ∑ n = 1 ∝ [ B l n S ( 1 − δ 1 l ) ( γ n r ) S ( 1 − δ 1 l ) ( γ n R ) + C l n T ( 1 − δ 1 l ) ( γ n r ) T ( 1 − δ 1 l ) ( γ n R ) ] cos [ γ n ( z + e 1 ) ] , ( 1 3 ) φ l r 3 = w l p + D l 1 r ( 1 − δ 1 l ) + ∑ n = 2 ∝ D l n cos [ β n ( z + e 1 ) ] I ( 1 − δ 1 l ) ( β n r ) I ( 1 − δ 1 l ) ( β n R ) 。 ( 1 4 ) φ l r 1 = ∑ n = 1 ∝ A l n cos [ λ n ( z + h 1 ) ] R ( 1 - δ 1 l ) ( λ n r ) R ( 1 - δ 1 l ) ( λ n R b ) ‚ ( 1 2 ) φ l r 2 = ∑ n = 1 ∝ [ B l n S ( 1 - δ 1 l ) ( γ n r ) S ( 1 - δ 1 l ) ( γ n R ) + C l n Τ ( 1 - δ 1 l ) ( γ n r ) Τ ( 1 - δ 1 l ) ( γ n R ) ] cos [ γ n ( z + e 1 ) ] , ( 1 3 ) φ l r 3 = w l p + D l 1 r ( 1 - δ 1 l ) + ∑ n = 2 ∝ D l n cos [ β n ( z + e 1 ) ] Ι ( 1 - δ 1 l ) ( β n r ) Ι ( 1 - δ 1 l ) ( β n R ) 。 ( 1 4 )
w l p = ( z + e 1 ) 2 − r 2 / 2 2 h 2 δ 1 l − ( z + e 1 ) 2 r − r 3 / 4 2 h 2 δ 3 l ; ( 1 5 ) { λ 1 = − i k , k t a n h ( k h 1 ) ω 2 / g γ 1 = − i k e , k e tanh ( k e e 1 ) ω 2 / g ‚ n = 1 ; ( 1 6 ) { λ n tan ( λ n h 1 ) = − ω 2 / g γ n tan ( γ n e 1 ) = − ω 2 / g ‚ n = 2 , 3 , ⋯ ; ( 1 7 ) β n = ( n − 1 ) π / h 2 。 ( 1 8 ) w l p = ( z + e 1 ) 2 - r 2 / 2 2 h 2 δ 1 l - ( z + e 1 ) 2 r - r 3 / 4 2 h 2 δ 3 l ; ( 1 5 ) { λ 1 = - i k , k t a n h ( k h 1 ) ω 2 / g γ 1 = - i k e , k e tanh ( k e e 1 ) ω 2 / g ‚ n = 1 ; ( 1 6 ) { λ n tan ( λ n h 1 ) = - ω 2 / g γ n tan ( γ n e 1 ) = - ω 2 / g ‚ n = 2 , 3 , ⋯ ; ( 1 7 ) β n = ( n - 1 ) π / h 2 。 ( 1 8 )
R ( 1 − δ 1 l ) ( λ 1 r ) = H ( 1 ) ( 1 − δ 1 l ) ( k r ) ‚ n = 1 ; ( 1 9 ) R ( 1 − δ 1 l ) ( λ n r ) = K ( 1 − δ 1 l ) ( λ n r ) ‚ n = 2 , 3 , ⋯ ; ( 2 0 ) S ( 1 − δ 1 l ) ( γ 1 r ) = H ( 1 ) ( 1 − δ 1 l ) ( k e r ) ‚ n = 1 ; ( 2 1 ) S ( 1 − δ 1 l ) ( γ n r ) = K ( 1 − δ 1 l ) ( γ n r ) ‚ n = 2 , 3 , ⋯ ; ( 2 2 ) T ( 1 − δ 1 l ) ( γ 1 r ) = H ( 2 ) ( 1 − δ 1 l ) ( k e r ) ‚ n = 1 ; ( 2 3 ) T ( 1 − δ 1 l ) ( γ n r ) = I ( 1 − δ 1 l ) ( γ n r ) ‚ n = 2 , 3 , ⋯ 。 ( 2 4 ) R ( 1 - δ 1 l ) ( λ 1 r ) = Η ( 1 - δ 1 l ) ( 1 ) ( k r ) ‚ n = 1 ; ( 1 9 ) R ( 1 - δ 1 l ) ( λ n r ) = Κ ( 1 - δ 1 l ) ( λ n r ) ‚ n = 2 , 3 , ⋯ ; ( 2 0 ) S ( 1 - δ 1 l ) ( γ 1 r ) = Η ( 1 - δ 1 l ) ( 1 ) ( k e r ) ‚ n = 1 ; ( 2 1 ) S ( 1 - δ 1 l ) ( γ n r ) = Κ ( 1 - δ 1 l ) ( γ n r ) ‚ n = 2 , 3 , ⋯ ; ( 2 2 ) Τ ( 1 - δ 1 l ) ( γ 1 r ) = Η ( 1 - δ 1 l ) ( 2 ) ( k e r ) ‚ n = 1 ; ( 2 3 ) Τ ( 1 - δ 1 l ) ( γ n r ) = Ι ( 1 - δ 1 l ) ( γ n r ) ‚ n = 2 , 3 , ⋯ 。 ( 2 4 )
式中, H (1) (1-δ 1l ) 、H (2) (1-δ 1l ) 分别为 (1-δ 1l ) 阶第一、二类Hankel函数, I (1-δ 1l ) 、K (1-δ 1l ) 分别为 (1-δ 1l ) 阶第一、二类变形Bessel函数。
在r =R b 处, 压力和法向速度连续性条件表达式分别为
φ l r 1 = φ l r 2 ‚ − e 1 ≤ z ≤ 0 ; ( 2 5 ) ∂ φ l r 1 ∂ r = { ∂ φ l r 2 ∂ R 0 − e 1 ≤ z ≤ 0 − h 1 ≤ z ≤ − e 1 。 ( 2 6 ) φ l r 1 = φ l r 2 ‚ - e 1 ≤ z ≤ 0 ; ( 2 5 ) ∂ φ l r 1 ∂ r = { ∂ φ l r 2 ∂ R 0 - e 1 ≤ z ≤ 0 - h 1 ≤ z ≤ - e 1 。 ( 2 6 )
在r =R 处, 压力和法向速度连续性条件表达式分别为
φ l r 2 = φ l r 3 ‚ − e 1 ≤ z ≤ − d 1 ( 2 7 ) ∂ φ l r 2 ∂ r = { δ 2 l + ( z − z c ) δ 3 l ∂ φ l r 3 ∂ r − d 1 ≤ z ≤ 0 − e 1 ≤ z ≤ − d 1 。 ( 2 8 ) φ l r 2 = φ l r 3 ‚ - e 1 ≤ z ≤ - d 1 ( 2 7 ) ∂ φ l r 2 ∂ r = { δ 2 l + ( z - z c ) δ 3 l ∂ φ l r 3 ∂ r - d 1 ≤ z ≤ 0 - e 1 ≤ z ≤ - d 1 。 ( 2 8 )
通过在上述连续性条件的两边同时乘上适当的特征函数, 然后在所考虑的区间进行积分, 使上面的连续性条件在z 区间上得到满足, 其具体推导和解法可参考文献[9 ] 。
《4 绕射速度势》
4 绕射速度势
《4.1基本方程和边界条件》
4.1基本方程和边界条件
在入射波作用下, 由于浮体不动, 而使波产生绕射, 在无旋、不可压缩条件下, 流体的空间绕射速度势ϕd 满足的基本方程和边界条件为
∂ 2 ϕ d ∂ z 2 + 1 r ∂ ∂ r ( r ∂ ϕ d ∂ r ) + 1 r 2 ∂ 2 ϕ d ∂ θ 2 = 0 , ( 2 9 ) ∂ 2 ϕ d ∂ z 2 + 1 r ∂ ∂ r ( r ∂ ϕ d ∂ r ) + 1 r 2 ∂ 2 ϕ d ∂ θ 2 = 0 , ( 2 9 )
∂ ϕ d ∂ z − ω 2 g ϕ d = 0 ‚ ( z = 0 , r ≥ R ) ( 3 0 ) ∂ ϕ d ∂ z - ω 2 g ϕ d = 0 ‚ ( z = 0 , r ≥ R ) ( 3 0 )
∂ ϕ d ∂ z = 0 , ( z = − h 1 , r ≥ R b ) ( 3 1 ) ∂ ϕ d ∂ z = 0 , ( z = - h 1 , r ≥ R b ) ( 3 1 )
∂ ( ϕ d + ϕ i ) ∂ z = 0 , ( 3 2 ) ∂ ( ϕ d + ϕ i ) ∂ z = 0 , ( 3 2 )
( z = − d 1 , r < R ; z = − e 1 , r ≤ R b ) ∂ ( ϕ d + ϕ i ) ∂ r = 0 , ( − d 1 < z < 0 , r = R ( z = - d 1 , r < R ; z = - e 1 , r ≤ R b ) ∂ ( ϕ d + ϕ i ) ∂ r = 0 , ( - d 1 < z < 0 , r = R
lim r → ∞ r √ ( ∂ ϕ d ∂ r − i k ϕ d ) = 0 lim r → ∞ r ( ∂ ϕ d ∂ r - i k ϕ d ) = 0
《4.2问题的求解》
4.2问题的求解
同求辐射势方法一样, 采用特征函数展开法求解上面的定解问题。 首先将流体计算域划分成I、II和Ⅲ 3个子域, 如图1所示, 这3个子域的辐射速度势分别记为ϕd1 、ϕd2 和ϕd3 。对每一子域采用分离变量法, 得到的表达式为正交函数的无穷级数 (它们满足除子域交界处外的所有边界条件) , 然后通过在交界处给出的压力及法向速度连续性条件来确定级数中的系数。ϕd1 、ϕd2 和ϕd3 表达式分别为
ϕ d 1 = ∑ m = 0 ∝ ∑ n = 1 ∝ A m , n cos [ λ n ( z + h 1 ) ] ⋅ R m ( λ n r ) R m ( λ n R ) cos m θ , ( 3 5 ) ϕ d 2 = − ϕ i + ∑ m = 0 ∝ ∑ n = 1 ∝ [ B m , n S m ( γ n r ) S m ( γ n R ) + C m , n T m ( γ n r ) T m ( γ n R ) ] ⋅ cos γ n ( z + e 1 ) cos m θ , ( 3 6 ) ϕ d 3 = − ϕ i + ∑ m = 0 ∝ { D m , 1 r m + ∑ n = 1 ∝ D m , n cos [ β n ( z + e 1 ) ] ⋅ I m ( β n r ) I m ( β n R ) } cos m θ 。 ( 3 7 ) ϕ d 1 = ∑ m = 0 ∝ ∑ n = 1 ∝ A m , n cos [ λ n ( z + h 1 ) ] ⋅ R m ( λ n r ) R m ( λ n R ) cos m θ , ( 3 5 ) ϕ d 2 = - ϕ i + ∑ m = 0 ∝ ∑ n = 1 ∝ [ B m , n S m ( γ n r ) S m ( γ n R ) + C m , n Τ m ( γ n r ) Τ m ( γ n R ) ] ⋅ cos γ n ( z + e 1 ) cos m θ , ( 3 6 ) ϕ d 3 = - ϕ i + ∑ m = 0 ∝ { D m , 1 r m + ∑ n = 1 ∝ D m , n cos [ β n ( z + e 1 ) ] ⋅ Ι m ( β n r ) Ι m ( β n R ) } cos m θ 。 ( 3 7 )
式中, λ n γ n β n R m S m T m
R m ( λ 1 r ) = H ( 1 ) m ( i λ 1 r ) = H ( 1 ) m ( k r ) ‚ n = 1 ; ( 3 8 ) R m ( λ n r ) = K m ( γ n r ) ‚ n = 2 , 3 , ⋯ ; ( 3 9 ) S m ( γ 1 r ) = H ( 1 ) m ( i γ 1 r ) = H ( 1 ) m ( k e r ) ‚ n = 1 ; ( 4 0 ) S m ( γ n r ) = K m ( γ n r ) ‚ n = 2 , 3 , ⋯ ; ( 4 1 ) T m ( γ 1 r ) = H ( 2 ) m ( i γ 1 r ) = H ( 2 ) m ( k e r ) ‚ n = 1 ; ( 4 2 ) T m ( γ n r ) = I m ( γ n r ) ‚ n = 2 , 3 , ⋯ 。 ( 4 3 ) R m ( λ 1 r ) = Η m ( 1 ) ( i λ 1 r ) = Η m ( 1 ) ( k r ) ‚ n = 1 ; ( 3 8 ) R m ( λ n r ) = Κ m ( γ n r ) ‚ n = 2 , 3 , ⋯ ; ( 3 9 ) S m ( γ 1 r ) = Η m ( 1 ) ( i γ 1 r ) = Η m ( 1 ) ( k e r ) ‚ n = 1 ; ( 4 0 ) S m ( γ n r ) = Κ m ( γ n r ) ‚ n = 2 , 3 , ⋯ ; ( 4 1 ) Τ m ( γ 1 r ) = Η m ( 2 ) ( i γ 1 r ) = Η m ( 2 ) ( k e r ) ‚ n = 1 ; ( 4 2 ) Τ m ( γ n r ) = Ι m ( γ n r ) ‚ n = 2 , 3 , ⋯ 。 ( 4 3 )
式中H ( 1 ) m m ( 1 ) H ( 2 ) m m ( 2 ) m 阶第一、二类Hankel函数, I m K m m 阶第一、二类Bessel函数。
同求辐射势一样, 剩下的问题就是确定未知系数A mn B mn C mn D mn r =R b 和r =R 处给出的压力和法向速度连续性条件来确定这4组系数。在r =R b 处, 压力和法向速度连续性条件确定的表达式为
ϕ d 1 = ϕ d 2 − e 1 ≤ z ≤ 0 , ( 4 4 ) ∂ ϕ d 1 ∂ r = ⎧ ⎩ ⎨ ∂ ϕ d 2 ∂ r − ∂ ϕ i ∂ r − e 1 ≤ z ≤ 0 − h 1 ≤ z ≤ − e 1 。 ( 4 5 ) ϕ d 1 = ϕ d 2 - e 1 ≤ z ≤ 0 , ( 4 4 ) ∂ ϕ d 1 ∂ r = { ∂ ϕ d 2 ∂ r - ∂ ϕ i ∂ r - e 1 ≤ z ≤ 0 - h 1 ≤ z ≤ - e 1 。 ( 4 5 )
在r =R 处, 压力和法向速度连续性条件确定的表达式为
ϕ d 2 = ϕ d 3 − e 1 ≤ z ≤ − d 1 , ( 4 6 ) ∂ ϕ d 2 ∂ r = ⎧ ⎩ ⎨ − ∂ ϕ i ∂ r ∂ ϕ d 3 ∂ r − d ≤ z ≤ 0 − e 1 ≤ z ≤ − d 1 。 ( 4 7 ) ϕ d 2 = ϕ d 3 - e 1 ≤ z ≤ - d 1 , ( 4 6 ) ∂ ϕ d 2 ∂ r = { - ∂ ϕ i ∂ r ∂ ϕ d 3 ∂ r - d ≤ z ≤ 0 - e 1 ≤ z ≤ - d 1 。 ( 4 7 )
通过一系列推导, 可从式 (44) ~ (47) 得到A mn B mn C mn D mn
Φ D = Re [ ϕ d ( r , θ , z ) exp ( − i ω t ) ] 。 Φ D = Re [ ϕ d ( r , θ , z ) exp ( - i ω t ) ] 。
《5 波浪激励力和辐射作用力的计算》
5 波浪激励力和辐射作用力的计算
《5.1波浪激励力的计算》
5.1波浪激励力的计算
波浪激励力是由辐射势之外的速度势作用产生的, 这些速度势一般包括入射势ϕi 和绕射势ϕd 。
F j = i ρ ω ∫ S ( ϕ i + ϕ d ) n ˜ j d s , ( 4 8 ) F j = i ρ ω ∫ S ( ϕ i + ϕ d ) n ˜ j d s , ( 4 8 )
{ n ˜ j } = ( n 1 , n 2 , n 3 , y n 3 − z n 2 , z n 1 − x n 3 , x n 2 − y n 1 ) { n ˜ j } = ( n 1 , n 2 , n 3 , y n 3 - z n 2 , z n 1 - x n 3 , x n 2 - y n 1 ) s 的单位法线矢量在正交坐标系轴上的投影, x , y , z 为转动参考点到ds 的矢径到坐标轴上的投影, j =1~6 (由于是柱对称问题, 所以可简单分为纵荡、垂荡和纵摇3种运动, j =1, 3, 5, 对应于l =2, 1, 3) 。下面根据式 (48) 列出了垂向波浪力表达式:
绕射力还可根据得到的辐射势ϕr 和入射势ϕi 进行计算, 即通过Haskind关系[8 ] 求解绕射力, 其表达式为
式中, S 0 为浮子与障碍物同流体接触的表面积之和, 由于表达式的繁杂, 这里就不列出有关表达式了。
《5.2辐射作用力计算》
5.2辐射作用力计算
辐射作用力是由于物体运动产生的辐射势对物体产生的作用力, 即
根据式 (52) , 可得l 运动模态在j 方向的辐射力为
式中, μ lj λ lj
《6 计算结果》
6 计算结果
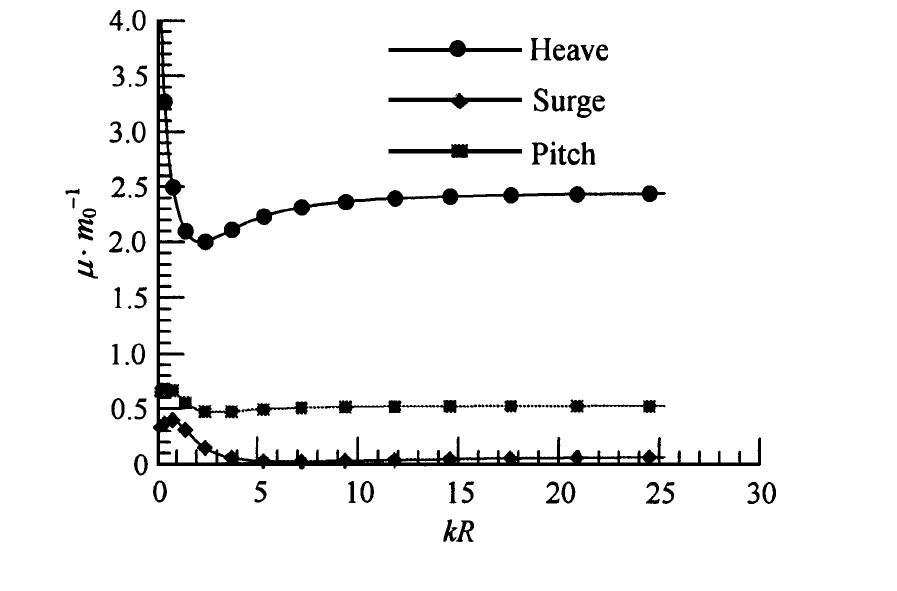
在线性规则入射波条件下, 为了验证有关表达式和程序运行的正确性, 我们在条件h 1 =2 m、d 1 =0.2h 1 、e 1 =0.5h 1 、R =R b =0.7h 1 下, 比较了2种方法相应物理量的计算结果。一种方法是同轴同半径障碍物条件下表达式, 另一种方法是同轴但半径大的条件下表达式, 比较结果如图2和图3所示。
《图9》
图2 附加质量
Fig.2 Added mass
《图10》
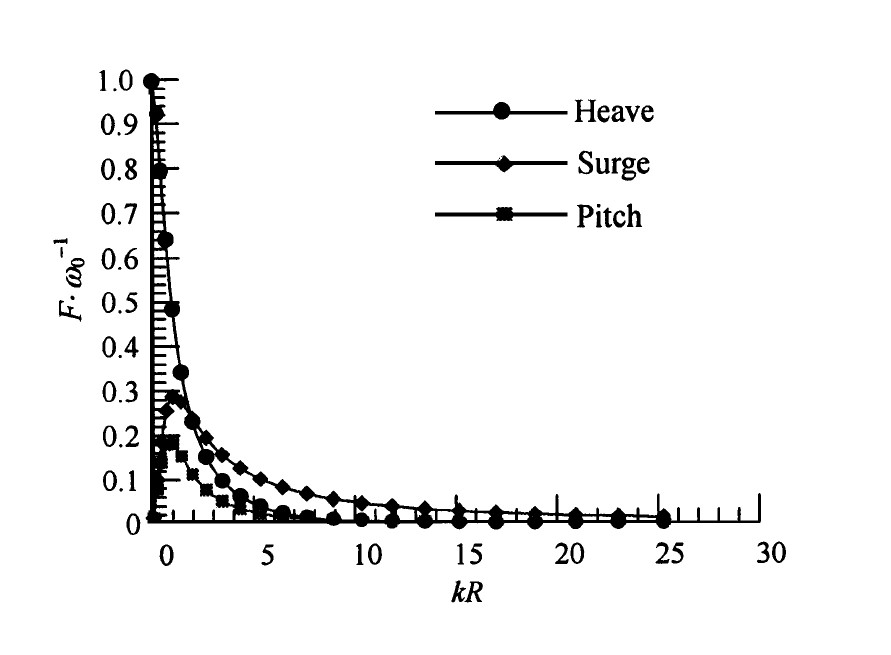
图3 激励力
Fig.3 Exciting force
在图2中, Heave是垂荡, Surge是纵荡, Pitch是纵摇, μ 为附加质量, m 0 =πρR 2 d 1 , μ /m 0 为无量纲附加质量系数, kR 是波数k 与浮子半径R 的乘积, 也为一无量纲量。图中线及线上的点 (包括圆形、棱形和方形) 代表不同运动模式的附加质量系数, 线代表文中相应表达式的计算结果, 点代表同轴同半径障碍物条件下相应表达式的计算结果 (另有论文论述) 。图3中, F 为垂向激励力, F /w 0 为激励力无量纲系数 (下面简称激励力系数) , 其中w 0 =ρg πR 2 。图中线和线上的点 (包括圆形、方形和棱形) 分别代表用2种方法由绕射势求解的激励力系数。两图表现的信息是2种方法计算的结果一致。
另外, 2种激励力表达式的计算结果的比较示于图4。
《图11》
图4 激励力比较
Fig.4 Comparison for the exciting forces
图中工况1指条件为d 1 =0.2h 1 , e 1 =0.45h 1 , R =0.5h 1 和R b =1.5h 1 ;工况2指条件为d 1 =0.3h 1 , e 1 =0.5h 1 , R =0.5h 1 和R b =3.5h 1 。线表示由式 (49) 和式 (50) 计算的结果, 点是由式 (49) 和式 (51) 的计算结果, 显然2种方法的计算结果一致。
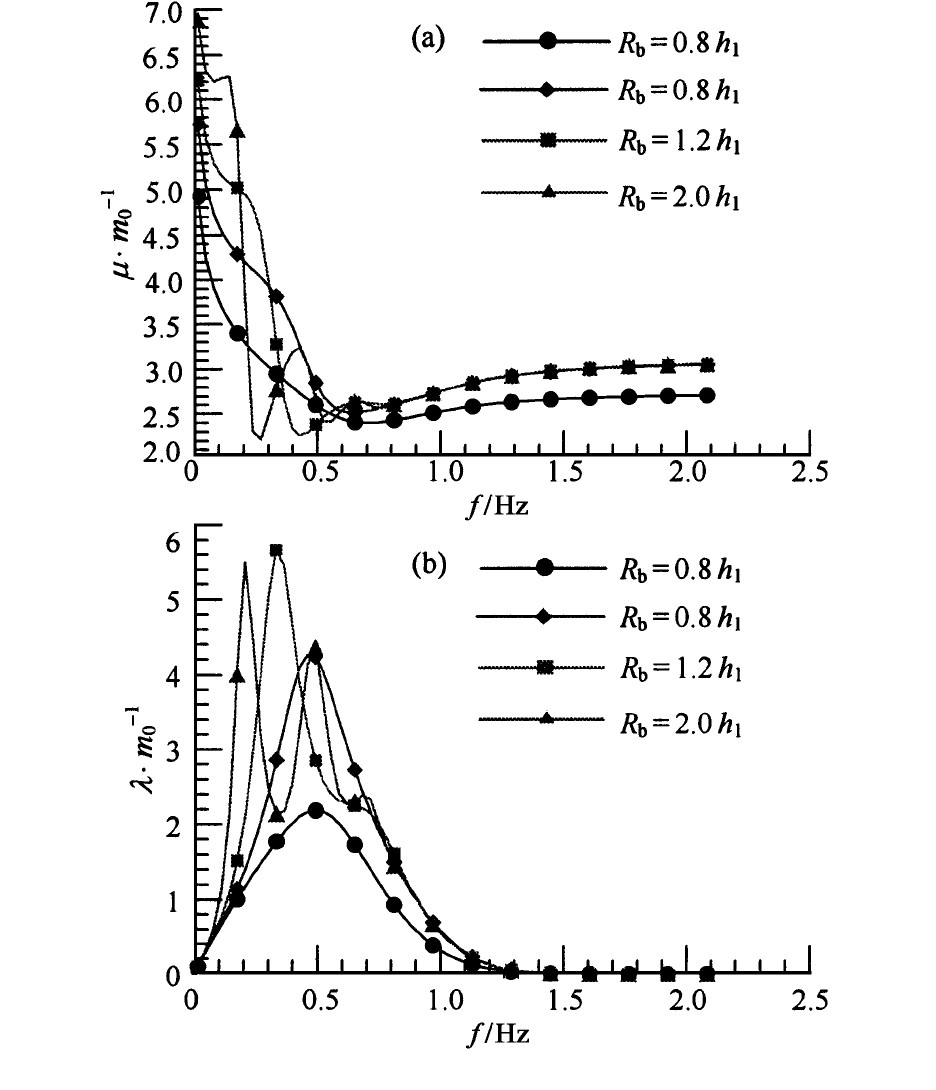
为了研究障碍物对浮体的附加质量、阻尼系数和激励力的影响, 这里以浮体作垂荡运动为例给出了一些算例, 如图5~图8所示。在图5~图8中, 除了在图2~图3中已说明的符号外, λ 为阻尼系数, λ /m 0 为无量纲阻尼系数, f 为入射波的频率, 图中的线和点 (包括圆形、棱形和方形) 代表不同条件下的附加质量系数、阻尼系数和激励力。图5~图6中, 表明了在d 1 =0.2h 1 、e 1 =0.3h 1 、R =0.5h 1 条件下, 附加质量、阻尼系数和激励力随障碍物半径R b 的变化情况。显然R b 小于某值时, 质量系数、阻尼系数和激励力随频率f 的变化比较平缓;当R b 大于某值时, 质量系数、阻尼系数和激励力随频率f 在低频段变化比较剧烈, 出现了多个极值, 在高频段比较平缓。
《图12》
图5 R b 的变化对附加质量和阻尼系数的影响
Fig.5 Added mass and damping coefficient with R b as a parameter
《图13》
图6 R b 的变化对激励力的影响
Fig.6 Exciting force with R b as a parameter
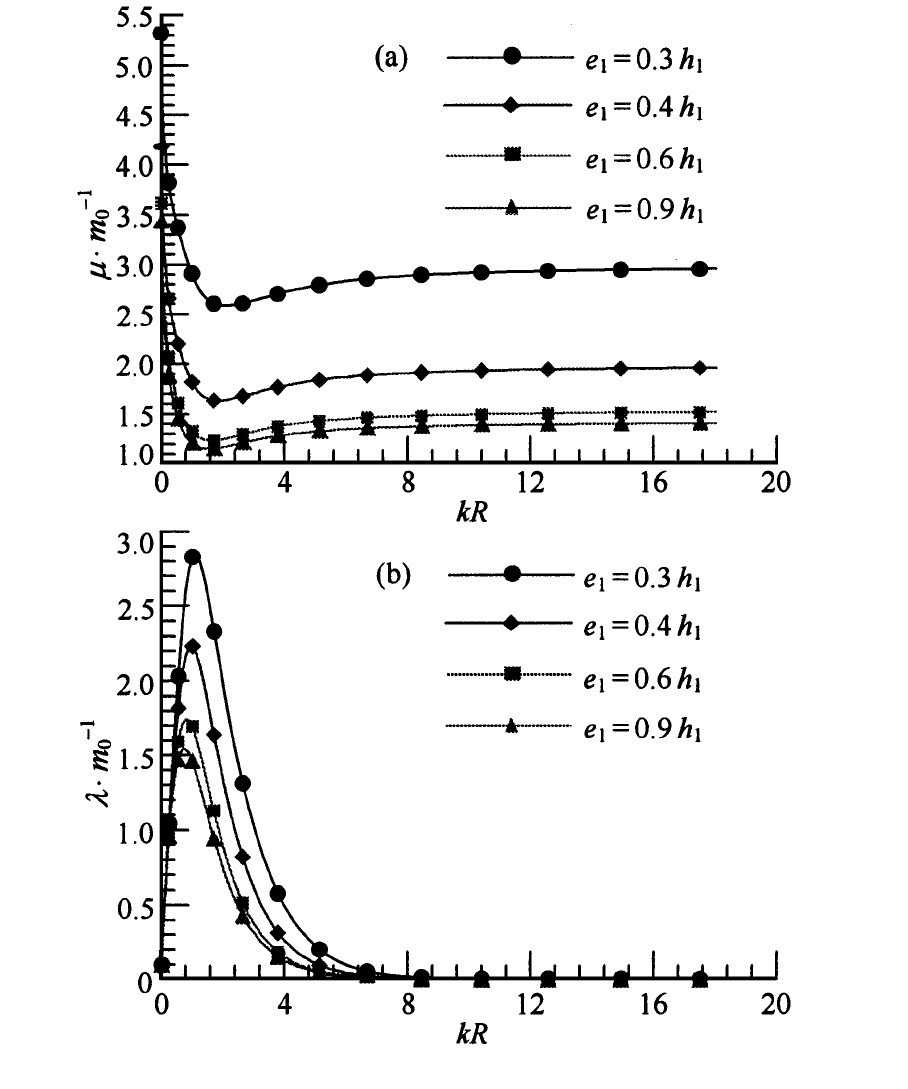
图7~图8中, 表明了在d 1 =0.2h 1 、R b =0.6h 1 、R =0.5h 1 条件下, 附加质量、阻尼系数和激励力随障碍物高度变化的变化趋势, 即两物体之间空隙变化的变化趋势。显然空隙越小, 附加质量、阻尼系数和激励力越大;附加质量、阻尼系数和激励力对不同的空隙随频率的变化不象半径R b 影响那么剧烈, 变化平缓;空隙的变化对垂向激励力的影响较小。
总之, 障碍物对浮体运动有很大影响, 特别是障碍物的半径会使浮体运动产生一些不平常的现象。
《图14》
图7 e 1 的变化对附加质量和阻尼系数的影响
Fig.7 Added mass and damping coefficient with e 1 as a parameter
《图15》
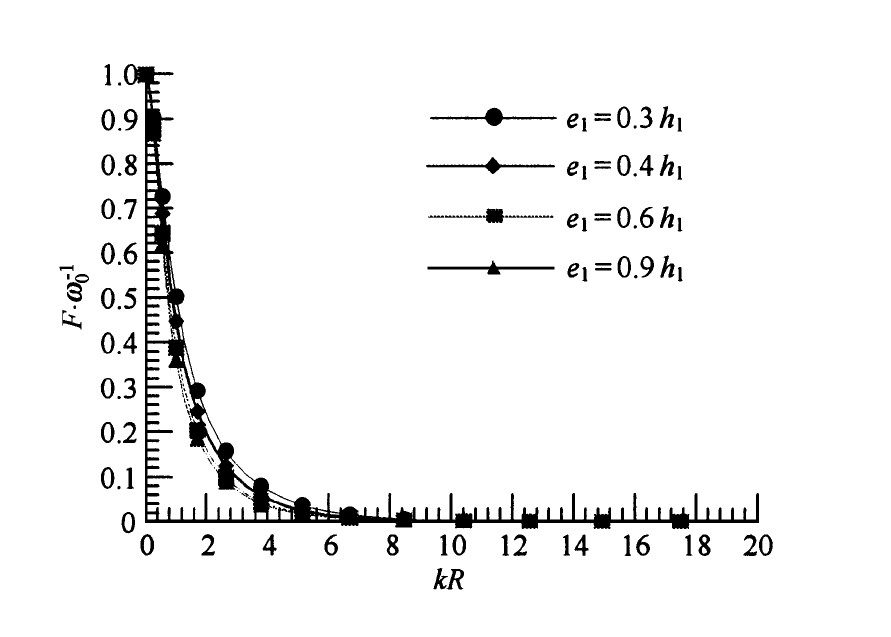
图8 e 1 的变化对激励力的影响
Fig.8 Exciting force with e 1 as a parameter
《7 结束语》
7 结束语
作者首先对线性规则入射波作用下的同轴但半 径大的障碍物地形上单浮体辐射和绕射问题采用分离变量法, 给出了辐射势和绕射势的解析表达式, 并根据辐射势、绕射势和入射势计算了水动力学系数和激励力;其次对推导的表达式的结果与同轴、同半径障碍物上单浮体的辐射和散射问题的结果进行了比较, 同时也比较了两种计算激励力的方法, 结果一致, 说明了作者推导的表达式是正确的, 编制的程序是可信赖的;最后讨论了同轴半径大障碍物对浮体的水动力学系数和激励力系数的影响, 结果表明障碍物对浮体的运动有很大的影响, 尤其是半径的变化对浮体运动有不平常的影响。
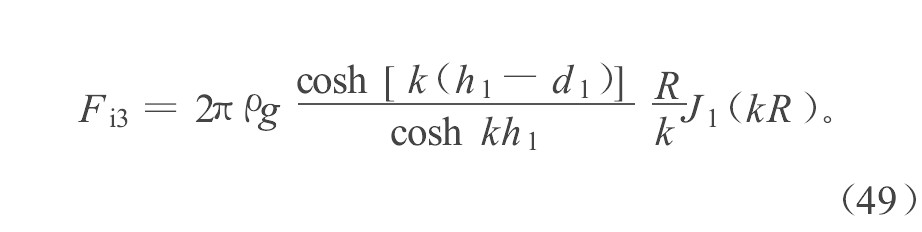
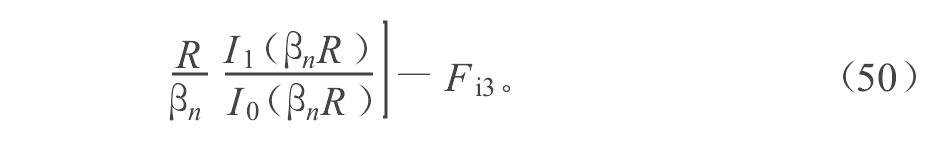

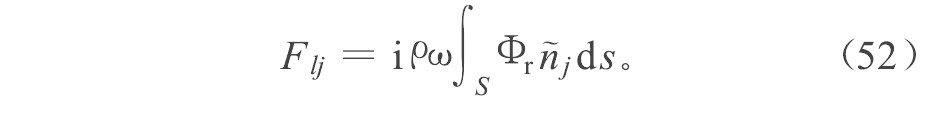

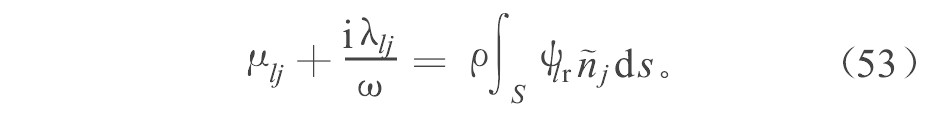
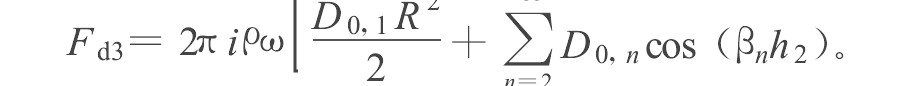















 京公网安备 11010502051620号
京公网安备 11010502051620号




