《1.引言》
1.引言
由于气候变化及人为影响，极端水文事件的发生频率和强度日益增加，已经造成了巨大的经济损失，并给居民及其生活环境带来了极大的影响[1–5]。在许多生态水文问题的管理中，推断某一特定事件（如洪水、干旱和风暴）在不同发生概率下的量级至关重要[6–8]。例如，在水利工程建筑设计中，大坝泄洪道的设计需要量化洪水事件的大小及发生频率[9]。然而，许多水文事件难以通过单一的变量来描述，并且其通常显示多种特征。一个典型的例子就是，洪水通常以其峰值流量、洪量和持续时间为特征。此外，洪水的这3个属性是相互关联的。然而，传统的单变量洪水风险分析主要集中在洪峰的概率特征上，这就难以提供洪水特征的完整描述（如对于洪峰、洪量和持续时间的依赖）。因此，多变量洪水频率分析对于深入描述极端水文事件以及推求可靠的风险预测是极其重要的[10,11]。
由于其描述相关变量间复杂相关关系的能力，copula函数已被广泛应用于生态水文问题中。具体而言，copula函数已被应用于许多洪水[10–13]、干旱[14,15]、暴风雨[16,17]等灾害的风险分析问题中。此外，该方法还被用于径流模拟[18–21]及其他能源以及环境系统分析问题中[22–25]。与传统的多变量统计方法相比，copula方法可以分别构建其边缘分布及相关性模型，因而可以使用不同类型的边缘和联合概率函数[2,13,26,27]。因此，在洪水风险分析中，可以通过各种参数或非参数分布来量化洪峰、洪量和持续时间的分布。例如，Karmakar和Simonovic[2]研究了边缘分布对基于copula函数多变量水文风险分析的影响。
水文风险分析的一个重要的问题是由于数据可用性、模型选择以及参数估计所导致的大量不确定性。不确定性有两个主要来源：①源于水文过程中固有变异性的自然不确定性；②源于系统不能完全解析所导致的认知不确定性[28]。尤其，数据可用性是洪水频率分析不确定性的主要来源。以前的一些研究已经解决了洪水风险分析中的不确定性问题。例如，Liang等[29]基于贝叶斯理论分析了模型和参数不确定性。然而，前人的大多数研究主要集中于单变量的水文风险上，很少有研究涉及多变量水文风险的不确定性分析。
因此，本研究旨在通过对洪水中多重属性的互动分析，提出一个多变量风险评估框架，其中将运用贝叶斯方法对双变量水文风险的不确定性进行评估。通过马尔可夫链蒙特卡罗（MCMC）方法，量化边缘和联合分布参数的后验概率，进而揭示首次双变量重现期的内在不确定性。
《2.方法》
2.方法
《2.1.Copula概念》
2.1.Copula概念
基于copula函数，可以构造一个多变量概率分布：
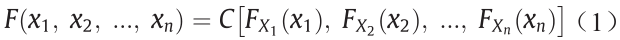
式中，FX1(x1),FX2(x2),...,FXn(xn)表示随机变量(X1,X2,…,Xn)的边缘分布。如果这些边缘分布是连续的，那么就存在一个copula函数C，如下式所示[13]：
式中，ui=FXi(x)；i=1,2,…,n。Nelsen[30]详细描述了copula的理论背景和性质。
当前已有许多copula函数可用于实际的多变量分析问题中，主要包括阿基米德、椭圆、极值copula函数。在本研究中将会使用阿基米德copula，因为其能够描述多种相关结构[31]。阿基米德copula可以采用多样的形式，此外，它们可以有不同的上尾和下尾相关特征。表1列出了在本研究中采用的copula函数及其固有特性。
《表1》
表1 Copula的基本性质
《2.2.条件分布》
2.2.条件分布
基于由方程（1）表示的copula函数，可以推出每个Xi的条件分布。以一个双变量分布为例，假设U1=FX1(x)，U2=FX1(x)，当U2=u2时，U1条件分布可被表示为[12]：
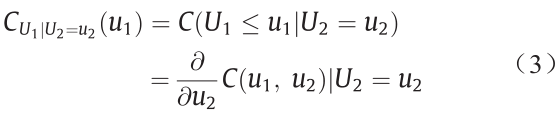
类似地，当U2≤u2时，U1条件分布可被表示为
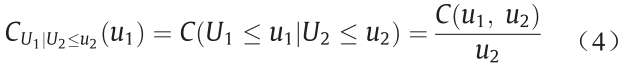
此外，一个copula的概率密度函数（PDF）c(u1,u2)可表示为：
然后，X1和X2的联合PDF可以由c(u1,u2)得出：
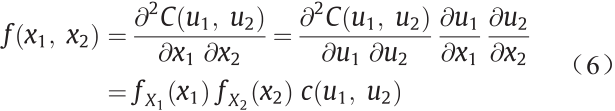
因此，对于给定的X2，X1的条件PDF表示为：
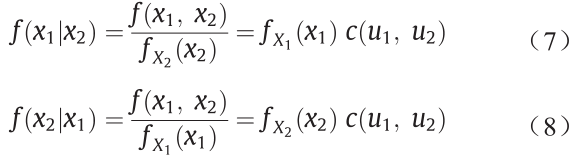
重现期已被广泛应用于单变量水文频率分析问题中。同理，可基于copula函数将重现期的概念扩展到多变量环境，从而形成了联合重现期的概念。具体地说，联合（首次）重现期可以进一步描述为“OR”和“AND”两种情况[13,32,33]：
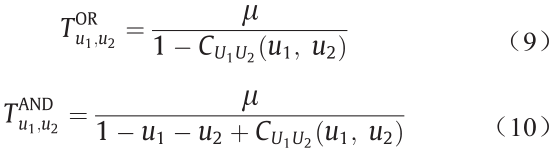
式中，μ表明了两个连续的极端事件的平均到达时间。
《2.3.双变量水文风险分析》
2.3.双变量水文风险分析
在实际的水利设施设计中，需要了解流经基础设施的洪水的随机特征。此外，一个洪水事件通常具有多重属性，如洪峰、洪量和持续时间。因此，多变量洪水风险比单变量洪水风险能够提供更多、更有用的信息。例如，一场具有高洪峰值和较长持续时间（如超过7d）的洪水可能会导致巨大的经济损失，而短期的高峰值洪水只会导致一场突如其来的山洪。因此，本研究基于“AND”联合重现期的构建了双变量风险指标以揭示洪水的多重属性之间的交互作用。该双变量风险指标可以表示为：
该双变量水文风险Ru1,u2可研究多个交互式洪水变量影响下的洪水风险水平。例如，对于一个具特定设计流量和服务年限的水利设施，如果u1和u2表示洪峰和洪量，Ru1,u2表示洪峰值大于设计流量时，其洪量大于阈值风险。因此，在本研究中，我们采用“AND”联合重现期来表示双变量水文风险。
《2.4.基于贝叶斯模型的参数估计》
2.4.基于贝叶斯模型的参数估计
基于copula函数风险模型中蕴含大量的不确定性，其原因包括：①洪水过程中固有的不确定性；②边缘分布和copula函数选择的不确定性以及③参数估计过程中的统计不确定性或参数不确定性（如样本的可得性）。贝叶斯方法已被广泛应用于不确定性量化问题。其可通过贝叶斯定理将各种信息来源整合到一个单独的分析框架中。根据先验概率密度和观察结果，其参数后验分布可以通过贝叶斯定理得到：
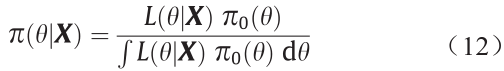
式中，π0(θ)表示先验概率分布；L(θ|X)表示似然函数；∫L(θ|X)π0(θ)dθ为归一化常数，π(θ|X)是后验概率密度函数。X=(x1,x2,…,xn)观察向量[在本研究中X=(x1,x2)]。
对于双变量水文风险分析，有必要对copula函数及两个边缘概率分布的参数进行估计。假设θc、θ1、θ2分别表示copula的参数及两个边缘概率分布的未知分布。基于贝叶斯定理，其后验分布可表示为：
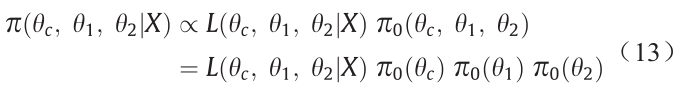
基于copula与其边缘分布之间的依赖结构，L(θc,θ1,θ2|X)为似然函数，可以表示为：
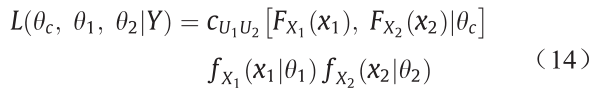
式中，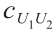
是copula函数的密度；
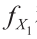和
分别是两个边缘PDF。
基于上述方法，本研究的多变量生态水文风险的具体计算过程如下。
步骤1：应用最大似然法估计边缘和copula中参数的初始值。
步骤2：计算边缘和联合概率的均方根误差（RMSE）和赤池信息量准则（AIC），以选择最合适的边缘和联合分布形式。
步骤3：根据步骤1中获得的参数值设置先验分布。
步骤4：使用MCMC与Metropolis-Hastings算法，推导出边缘和联合分布中参数的后验概率。
步骤5：评估首次和联合重现期的不确定性。
步骤6：揭示双变量水利风险的概率特征。
《3.应用》
3.应用
《3.1.流域特征与数据》
3.1.流域特征与数据
该方法被应用于中国三峡库区香溪河流域的水文风险分析。香溪河位于三峡库区湖北段。如图1所示，香溪河起源于神农架自然保护区，是长江的主要支流之一，干流长度为94km，流域面积为3099km2[34]。该区域为北亚热带气候，年平均降水量为1100mm，波动范围为670~1700mm[35]。香溪河流域汛期为7~8月，主要降雨时节为5~9月。本研究利用兴山水文站（东经110°45′0″，北纬31°13′0″）观测到的日流量数据（1961—2010年），对香溪河洪水风险进行了概率评估。
《图1》
图1.所研究流域的位置。DEM：数字高程模型。
《3.2.香溪河洪水特征》
3.2.香溪河洪水特征
在本研究中，洪水特征是通过峰值、洪量和持续时间来确定的，其中洪峰是最大洪峰流量，而洪水量和持续时间是通过最大流量的水文图得到的。根据Yue[36,37]的研究，可以通过洪水过程线的上升（图2中的Dsi）和下降（Dei）时刻来获得第i年中单峰洪水过程（图2[31]）的持续时间（Di）。如图2所示，一次洪水的起始时间由水文图的急剧上升为标记，而洪水的终点由曲线[10]的后退支点上的拐点确定。如果洪水的上升时刻用Ds（d）表示，结束时间用De（d）表示，那么洪水事件的洪水量可用下式表示：
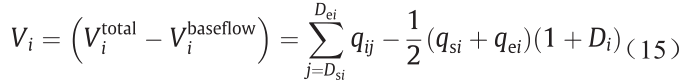
式中，qij是第i年第j天的观测径流；qsi是第i年洪水开始日的洪水流量；qei是洪水结束日的径流值。Dsi和Dei分别表示第i年洪水的开始和结束日，能够由下式得到：
年洪水极值通过下式得到：
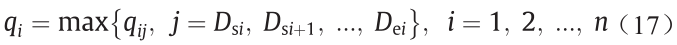
基于方程（15）~（17），洪水特征可以通过其峰值、洪量和持续时间来识别。表2显示了兴山站的洪峰、洪量和持续时间的统计特征。峰度和偏度都是正值，表明洪水变量可以用尖峰和右尾分布来模拟。
《图2》
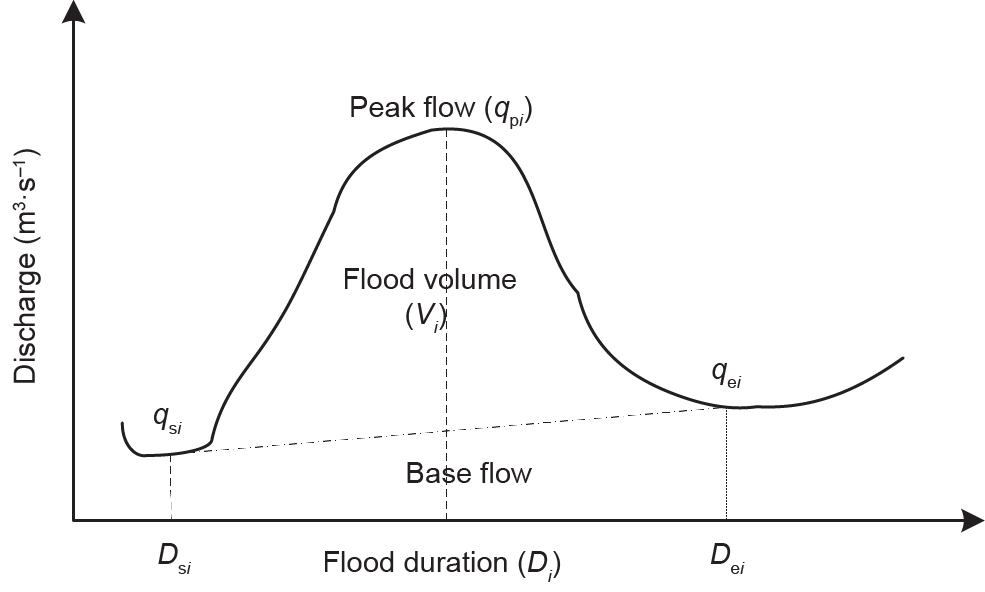
图2.典型的洪水过程曲线图（改编自文献[31]）。
《表2》
表2 洪水变量的统计特征
《4.边缘分布和联合分布的初始参数值》
4.边缘分布和联合分布的初始参数值
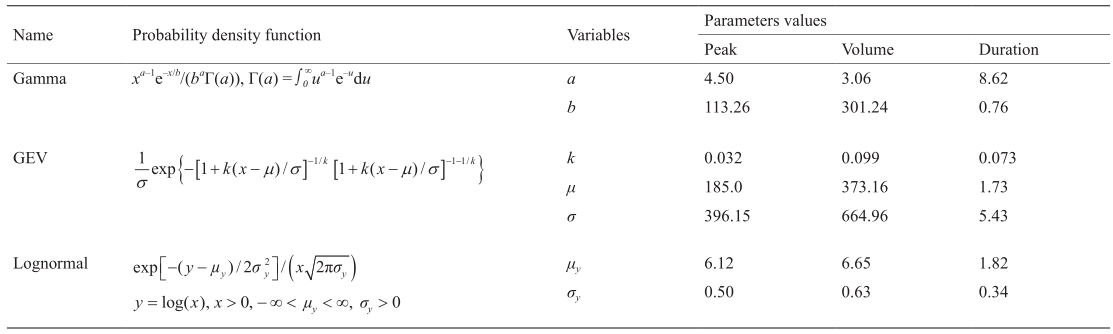
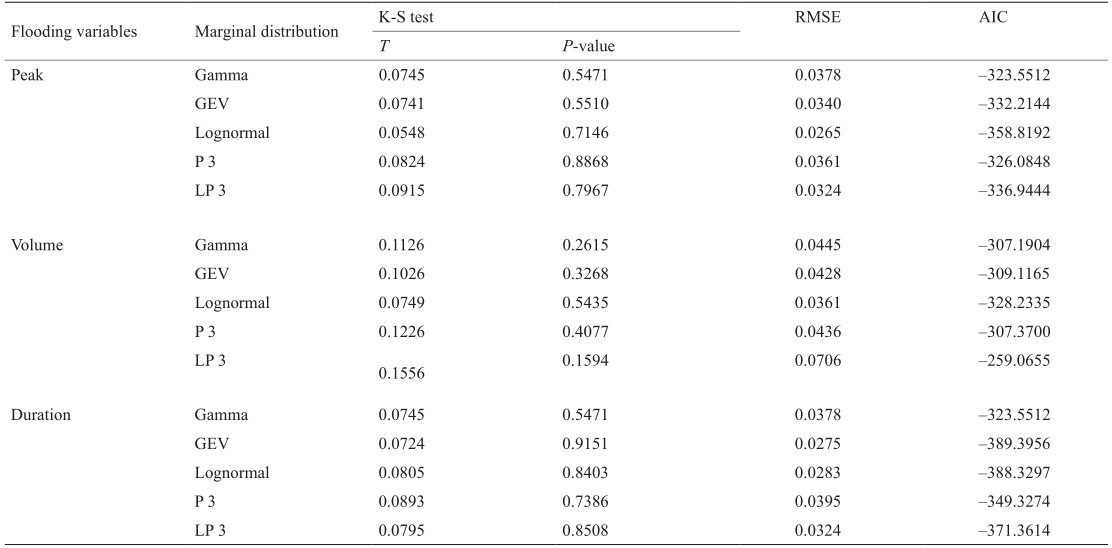
对于洪峰等单变量，许多参数化的分布函数可用于量化其概率特征，如广义极值分布（GEV）、对数Pearson TypeⅢ（LP3）和Pearson TypeⅢ（P3）[38,39]。在本研究中，Gamma、GEV和对数正态分布将被用来量化洪水洪峰、洪量和持续时间的概率特征，并基于最大似然估计（MLE）方法估计这些分布中的未知参数。表3给出了由MLE获得的分布函数的具体公式及未知参数的估计值。图3给出了理论分布和观测值之间的比较。应用RMSE和AIC准则来评价每个边缘分布的表现，如表4所示。结果表明，对数正态分布在香溪河3个洪水变量中表现最好。
《表3》
表3 洪水变量的边缘分布函数
《表4》
表4 洪水变量不同分布函数的RMSE及AIC值的对比
《图3》
图3.观测概率与不同概率密度模型的观测值对比。
表5给出了3个洪水变量（即洪峰值、洪量和持续时间）之间线性相关系数和Kendall（τ）系数的值。结果表明，洪峰与洪量的相关性最高，其次是洪量和持续时间以及洪峰和持续时间。为了量化洪峰-洪量、洪量-持续时间和洪峰-持续时间的相关特征，采用了Ali-Mikhail-Haq（AMH）、Cook-Johnson（Clayton）、Gumbel-Hougaard和Frank copula这4个阿基米德copula函数，基于Kendall系数的反推通过矩量法（MOM）样估计器来估计它们的未知参数。用copula函数来量化洪水变量之间的相关性，利用RMSE和AIC对copula函数表现进行评价。表6显示了不同的copula函数用于模拟洪峰-洪量、洪量-持续时间和洪峰-持续时间的联合分布的RMSE和AIC结果。结果表明，通过Frank copula可以较好地量化洪峰-洪量、洪量-持续时间的联合分布，而洪量-持续时间的联合分布可以通过Ali-Mikhail-Haq得到较好的结果。
《表5》
表5 洪水变量间的相关系数的取值
《表6》
表6 不同copula函数的RMSE和AIC值的对比
《5.双变量水文风险不确定性分析》
5.双变量水文风险不确定性分析
为了进一步分析基于copula函数的风险分析模型的不确定性，本研究将假定模型参数的先验分布为正态分布，其均值为MLE及MOM得到的值，方差则人为假定比较大的值。表7给出具体的先验分布信息。基于MCMC计算5000次，并将最后500次设定为copula模型参数的后验分布。图4展示了边缘分布及copula函数中参数的演进过程。结果显示贝叶斯方法得到的参数最后趋于稳定并集中于某个固定值附近。图5给出了参数的后验分布信息。基于MCMC所得到的样本，可推求设计值的概率特征，其不仅可给出具体的设计值，还能得到相关的预测区间。
《表7》
表7 贝叶斯模型中各参数的先验分布
《图4》
图4.MCMC过程中未知参数的演变。（a）洪峰；（b）燃烧阶段后。
《图5》
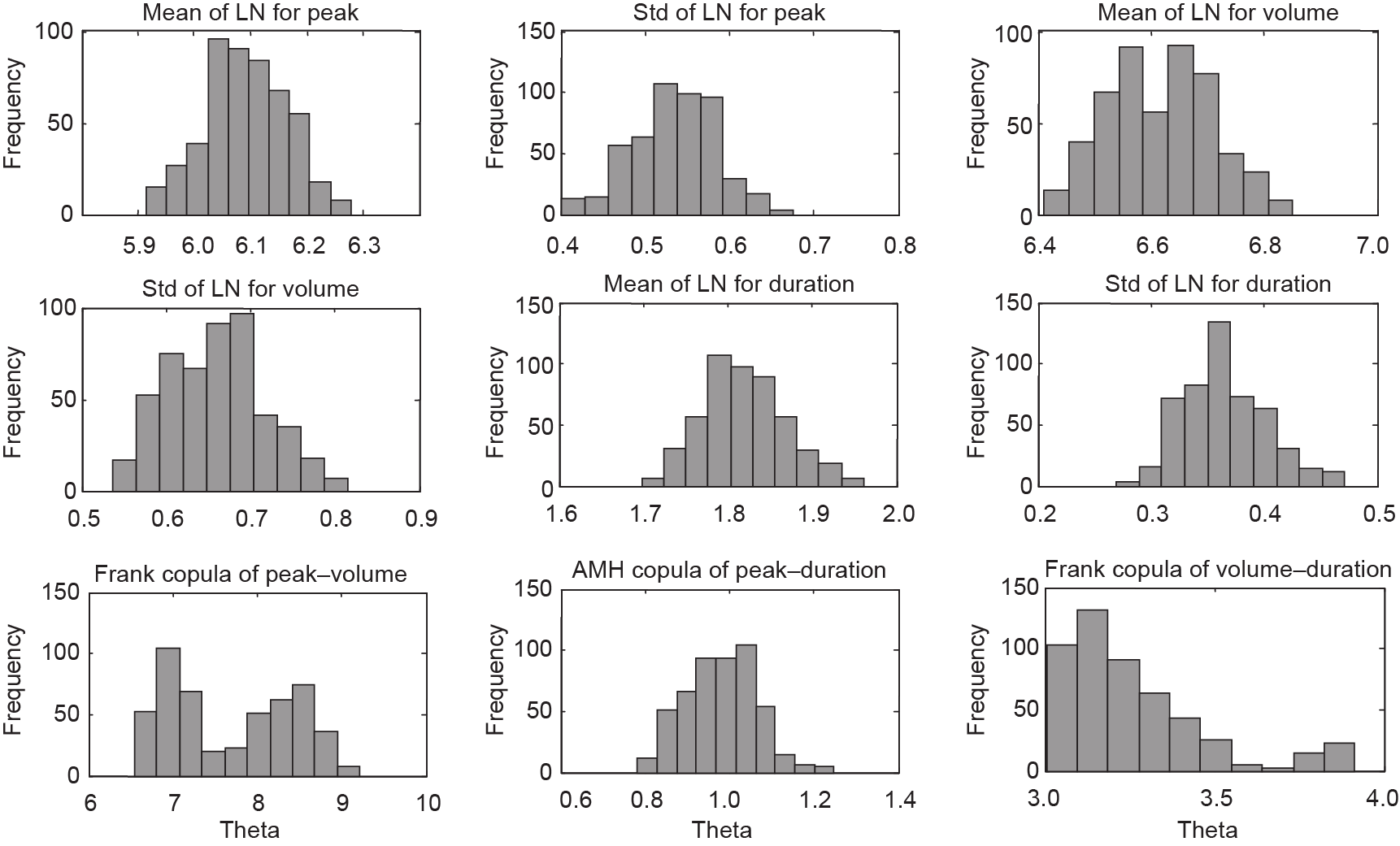
图5.边缘分布及copula函数中未知参数的后验概率。LN对数正态分布。
在本研究中，基于贝叶斯方法推求的边缘分布及copula函数中参数的值表现为一定的概率分布，进而导致了洪水变量边缘及联合分布的不确定性。图6给出了预测均值与观测值之间的对比，此外还给出了95%置信度水平下的预测区间，预测值分别为2.5%和97.5%分位数。该图显示所得到的预测区间可很好地覆盖对应观测概率。此外，对洪水持续时间而言，图3显示MLE所得到的概率分布于观测概率存在明显偏差。这可能是由于洪水持续时间的数据所导致。在本研究中，所有数据均为日尺度，因此洪水持续时间也表示为天数，进而导致洪水持续时间的概率分布蕴含大量不确定性。与之相比，图6结果显示基于贝叶斯方法所得到的95%预测区间能够覆盖大部分的洪水持续时间的观测概率值。
《图6》
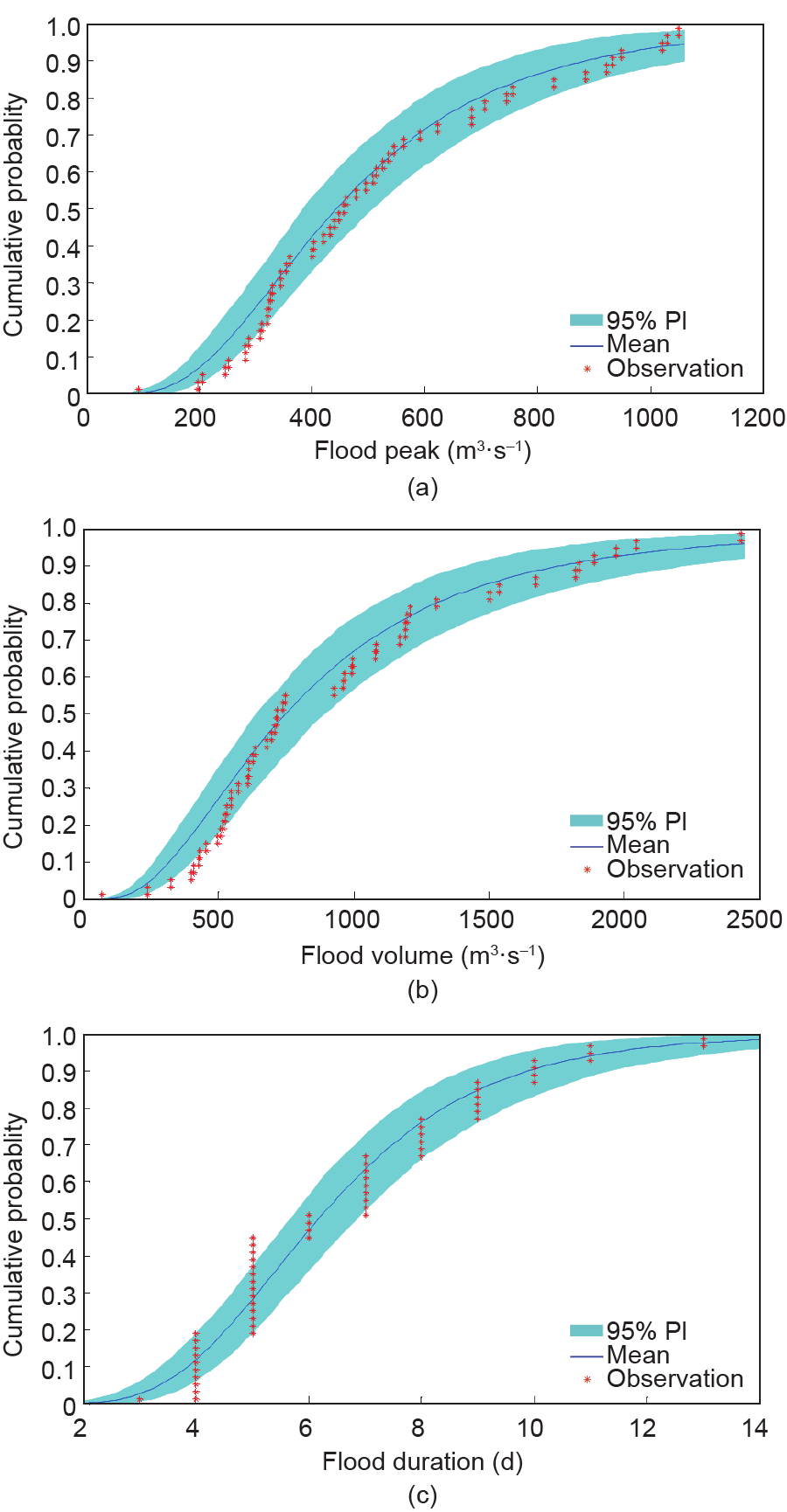
图6.预测概率与观测概率值间的对比。（a）洪峰；（b）洪量；（c）洪水持续时间。
在贝叶斯的方法框架中，位置参数被设置为随机变量，并且设定相关先验分布；而其后验分布则通过MCMC来推求。同时，边缘分布及联合分布中参数的随机性又导致相关条件累积分布函数（CDF）及条件PDF的不确定性。图7给出了给定洪峰为95%分位数情景下的洪量及洪水持续时间的条件CDF分布；基于参数后验分布，可进一步推求所得条件CDF的预测区间。此外，通过公式（7）和公式（8），可推导不同重现期洪峰情景下的洪量及洪水持续时间的条件PDF。图8显示了不同洪峰重现期情景下的条件PDF。假设考虑两种洪峰情景（10年和100年重现期），所得洪量及洪水持续时间条件概率密度分布显示随着洪峰值的增加，洪量的值也会增加，而与此同时，洪水持续时间可能不会有很大变化。
《图7》
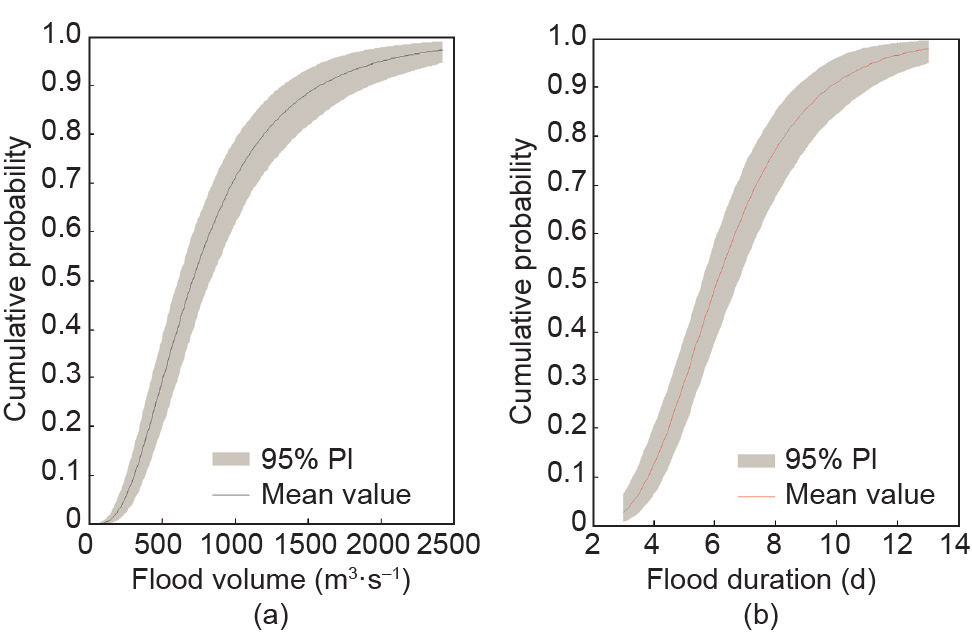
图7.95%洪峰分位数情景下的条件CDF。（a）洪量；（b）持续时间。
《图8》
图8.不同洪峰重现期情景下的条件PDF。（a）洪量；（b）持续时间。
基于公式（9）~（12）所得联合重现期可很好地反映洪峰-洪量、洪峰-持续时间及洪量-持续时间共同发生的概率水平。此外，模型参数的随机特征也同时导致了上述联合重现期的不确定性。表8给出了洪水的单变量及联合重现期的95%预测区间。此外，随着单变量重现期的增加，所对应的洪峰、洪量及持续时间预测值的不确定性也会增加。例如，一次5年重现期洪水事件的洪峰的95%变化区间为[594.1,813.9]m3·s–1，而如果重现期为100年，其95%变化区间为[1156.3,2007.1]m3·s–1。对于联合重现期，如表8所示，一个明显特征是“OR”联合重现期的不确定性不会有很大变化。与之相比，“AND”联合重现期和二次重现期的不确定性特征与单个洪水变量的重现期类似，如表8所示。例如，初始重现期为100年所对应的联合重现期
的95%预测区间为[1229.4,1593.8]年；而相应的联合重现期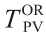
的95%预测区间为[51.62,52.12]年。
《表8》
表8 单变量重现期及首次重现期的95%预测区间
本研究提出了一种两变量风险指标，如公式（12）所示，以反映洪水变量间的相互作用以及它们对具体洪水风险的潜在影响。对于一个洪水事件，水利设施的损坏主要由于高洪峰量，因此分析洪水风险时必须考虑洪峰量。所以，本研究将分析洪峰-流量及洪峰-持续时间的联合风险。图9展示了不同设计流量及服务时间情景下洪水风险随洪量的变化趋势。对于所有的设计流量及服务时间情景，洪峰和洪量的两变量风险会在一定洪量范围内保持稳定，然后会随洪量的增加而减少。此外，对于某个洪峰-洪量组合，由于边缘分布和联合分布的参数不确定性，其具体风险水平也会是不确定的。基于参数的后验概率，可推求双变量风险的预测均值及95%预测区间，如图9所示。结果显示，低设计流量和高服务年限会导致水文风险的高不确定性。图10展示了兴山站附近堤坝在不同洪峰-持续时间情景下的水文风险。结果显示对于同样的服务时间，水文风险随设计流量的增加而降低。类似地，对于同样的设计流量，增加服务时间会同时增加水文风险。同时，洪峰-持续时间双变量风险的不确定性特征与洪峰-洪量类似。
《图9》
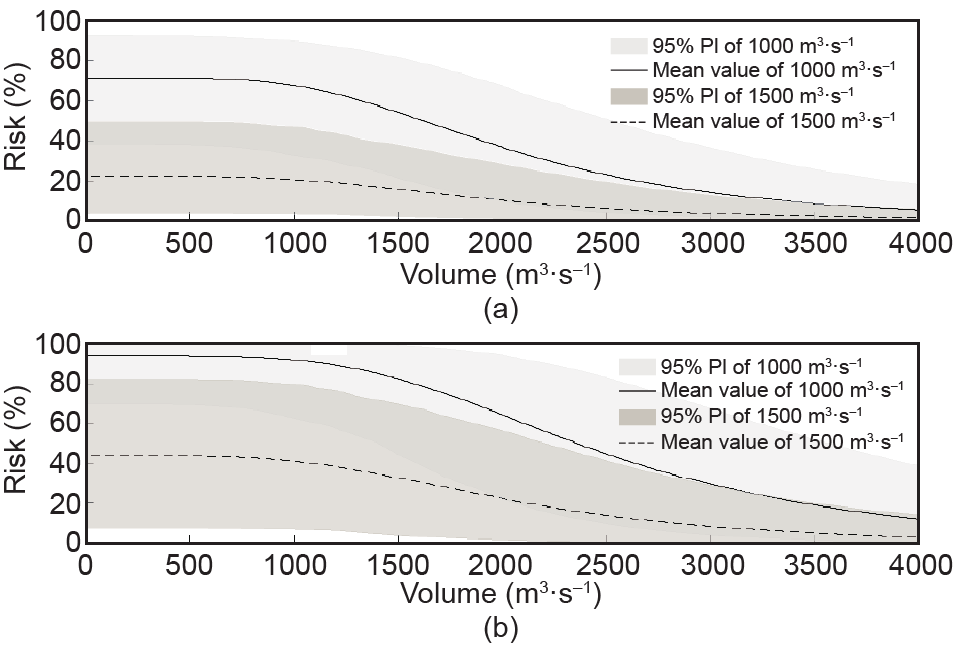
图9.不同洪量-洪峰组合情景下的双变量洪水风险。（a）20年服务时间；（b）50年服务时间。
《图10》
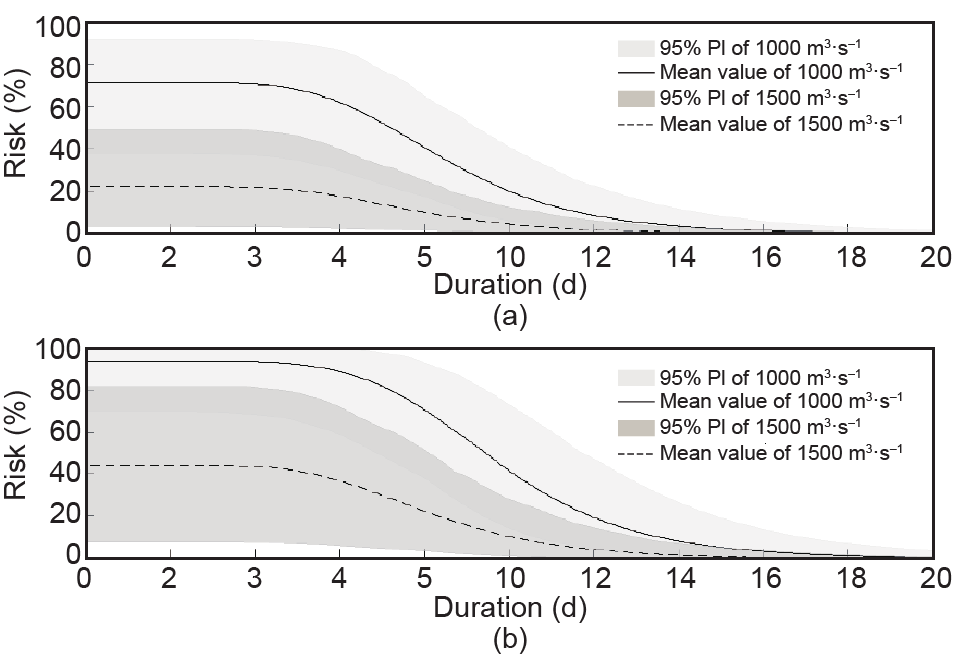
图10.不同洪量-持续时间组合情景下的双变量洪水风险。（a）20年服务时间；（b）50年服务时间。
《6.结论》
6.结论
Copula函数是水文及水资源领域应用最广泛的方法之一。许多研究基于copula函数开展多变量环境下的水文灾害（如洪水、干旱等）风险分析。然而，前人的研究在一定程度上忽略了copula模型框架中边缘分布及联合分布的参数不确定性。本研究旨在辨识多变量水文风险中的内在不确定性。本研究的创新之处在于将贝叶斯理论引入到copula模型框架中用于量化边缘分布及相关性结构中参数的不确定性。同时，进一步揭示边缘分布和联合分布参数不确定性间的互动关系。该研究通过分析香溪河流域生态水文风险来阐述其应用性。
研究结果显示，对数正态分布比较适合量化香溪河流域洪水变量的边缘分布。就联合分布而言，Frank copula适合于量化洪峰-洪量、洪量-持续时间的联合分布；Ali-Mikhail-Haqcopula则适合于构建洪峰-持续时间的联合分布。MCMC方法用于量化边缘分布及联合分布的参数不确定性，其结果显示所得预测区间能够很好地覆盖观测概率，尤其对洪水持续时间而言。此外，基于模型参数后验概率分布，可推求“AND”和“OR”联合重现期的95%预测区间。所得结果显示“AND”联合重现期的不确定性将随单变量重现期的增加而增大，但“OR”联合重现期的不确定性不会随之剧烈变化。最后，该研究还揭示了洪峰-洪量、洪峰-持续时间两组双变量水文风险的不确定性，以反映洪水变量间对水利设施损失风险的互动效应。
自从De Michele和Salvadori[40]将copula函数引入水文分析以来，此类方法已被广泛应用于多变量水文风险分析问题中。本研究将贝叶斯方法引入到copula模型框架中以辨识多变量水文风险分析中的内在不确定性，并进一步揭示洪水变量（如洪峰、洪量和持续时间）不确定性的互动效应对相应风险预测的影响。通过香溪河的实例证明该方法的可靠性。但是该方法还可用于其他水文事件（如干旱、暴雨等）在不同区域的风险分析问题中。
本研究尝试评估基于copula的多变量水文风险分析中的不确定性。然而，该研究需要进一步拓展以分析模型选择及其他不确定来源所导致的水文风险不确定性。
《Acknowledgements》
Acknowledgements
This work was jointly funded by the National Natural Science Foundation of China (51520105013 and 51679087) and the National Key Research and Development Plan of China (2016YFC0502800).
《Compliance with ethics guidelines》
Compliance with ethics guidelines
Yurui Fan, Guohe Huang, Yin Zhang, and Yongping Li declare that they have no conflict of interest or financial conflicts to disclose.
京公网安备 11010502051620号
