《1. 引言》
1. 引言
混凝土材料中的碱硅反应(ASR)是水泥浆中所含的碱金属离子与骨料中存在的活性硅成分在潮湿环境下发生的一种化学反应。ASR产生了一种膨胀凝胶,通常被称为“ASR凝胶”,随着时间的推移,ASR凝胶会引起混凝土的破坏和开裂[1]。随着材料的长期劣化,混凝土的刚度和强度都会下降。ASR发生的关键因素是水的存在,这就是为什么ASR是影响高湿度环境(通常高于60%)下混凝土结构的主要原因。温度是控制ASR发生的另一个关键因素[2]。
Stanton [3]是第一个研究ASR效应的人,他研究了ASR的化学性质及其对材料和结构方面的影响,开发了用于评估混凝土混合料配合比及骨料分布对ASR效应的实验技术,设计了新的减轻ASR损坏的解决方案。之后,许多研究工作,包括实验、分析和数值研究,都仔细考虑了ASR的存在及其对结构劣化等各方面的影响。
实验室条件下的ASR实验主要是在加快ASR情况下采用小规模标本进行的。快速砂浆棒试验(AMBT)[4]是一种流行的实验方法,试验大约持续16 d。在AMBT实验中,将由粉碎的骨料铸成的样品浸入碱性溶液中,并将温度升至80 ℃。另一个ASR实验方案是混凝土棱柱体试验(CPT)[5],该方法提供了有关ASR对混凝土结构影响的更全面的数据。CPT通常采用由工业应用中的骨料浇铸而成的混凝土样品进行,无需进行任何调整。此外,样品需要被保存在完全密封的容器中,湿度要接近饱和状态(97%或更高),从而确保最大的水分含量并最大限度地减少沥滤。CPT按实验持续时间可分为两类:加速试验通常在60 ℃下进行,持续时间为6个月;而长期试验则在38 ℃下进行,持续时间为1~2年。
许多研究人员探索了不同长度和不同精度水平下的ASR效应的数值模型。Bažant等[6]首先通过断裂力学方法探讨了ASR的损伤和劣化,并预测了骨料劣化尺寸。
文献中包含了几种宏观连续体模型,用于研究ASR机制及其与混凝土力学性能退化的关系。其中最早的一种是由Charlwood等[7]和Thompson等[8]开发的现象学模型。后续开发出的更详细的模型,如参考文献[9]描述的模型以及将蠕变效应考虑在内的其他模型[10],都可成功预测整个结构的应力和变形过程。此外,研究人员根据ASR动力学建立了计算模型,并使用裂纹带法将其运用到各种有限元软件程序中[11,12]。这些模型成功地复制了一些有关ASR扩展的实验数据[13]。应力状态对ASR劣化机制的影响被纳入Saouma和Perotti [14]以及Multon等[15]所开发的模型中。Comi等[16,17]开发了一种损坏模型,该模型考虑了ASR过程中某些力学和化学方面的热力学规律。Poyet等[18]将温度和湿度因素整合到ASR的动力学中。最后,Bažant等[19,20]构建了一个ASR劣化的微平面模型,其中由ASR凝胶流动所引起的压力是主要的劣化机制。上述模型都可以被用来研究ASR机制及其与混凝土力学性能退化的关系,但是Capra和Sellier [21]提出了一种基于ASR关键参数和与混凝土力学性能相关的概率分析方法来研究ASR。
然而,上述力学模型有一个共同的缺点,那就是不能准确地再现由ASR所引起的裂纹图案和损伤分布。这限制了对由ASR效应引起的混凝土力学性能退化的现实预测,并需要使用唯象公式将混凝土力学性能与ASR凝胶膨胀联系起来。这些模型还需要利用唯象关系去耦合应力状态下的ASR凝胶膨胀,以再现混凝土约束下的ASR效应。这些限制的产生主要是由于假定了混凝土是各向同性均质材料[22]。第一个能够成功克服这些限制的力学模型是ASR-LDPM [23],该模型已被用于目前的研究。在该模型中,ASR效应与晶格离散粒子模型(LDPM)相结合[24,25]。LDPM是一个离散的力学模型,它将混凝土模拟成一个由三维(3D)刚性多面体单元组成的整体,每个多面体单元代表一个球形骨料及砂浆。这些细胞通过晶格支撑连接,其力学行为以矢量形式表示。以往的研究表明,ASR-LDPM可以成功复制自由膨胀试验和多轴压缩试验中的裂纹分布和图案[23]。此外,ASR-LDPM成功地再现了温度和碱含量对混凝土力学性能退化的影响。这里需要注意的是,在ASR-LDPM公式中,ASR凝胶膨胀与混凝土力学性能退化之间不存在唯象关系。在最近的研究中,蠕变和收缩效应也被纳入该模型,这对于改善模型预测多变的温度和湿度来说是非常必要的[26,27]。
尽管ASR-LDPM框架具有强大的功能,但该模型仍存在局限性——大型混凝土结构构件的仿真计算成本很高。因此,为了解决实际问题,必须开发一种多尺度框架以降低分析的计算成本,同时又要保持结果的准确性。Wu等 [28]建立了基于平均定理的均质化框架,以分析混凝土结构中的ASR效应。但是,他们没有进行两尺度均质化分析,也没有研究多尺度模型的数值准确性和计算效率。在目前的研究中,新开发的多尺度均质化框架[29–32]被用于研究ASR对混凝土结构的影响。通过将ASR-LDPM代表性体积元(RVE)均质化为宏观张量本构关系,利用传统的有限元方法可以模拟宏观问题,并显著降低解决这些问题所需的计算成本。
《2. ASR-LDPM 模型回顾》
2. ASR-LDPM 模型回顾
ASR-LDPM模型[23]是通过将ASR引起的中尺度应变引入由LDPM模拟的混凝土中尺度力学相互作用中所建立起来的。ASR应变随时间和空间的演变与所要解决的问题的化学-物理性质有关,由其引发的劣化问题仅取决于LDPM的本构行为。下面的小节将回顾LDPM和ASR模型的公式,然后解释它们是如何被耦合的。
《2.1. 晶格离散粒子模型》
2.1. 晶格离散粒子模型
使用混凝土混合料配合比作为输入数据(即水泥含量c、水灰比w/c 和骨灰比 ),通过以下步骤构建一个通用LDPM系统的中尺度几何构型:
),通过以下步骤构建一个通用LDPM系统的中尺度几何构型:
(1)通过反复试验,将假定为球形的粗骨料插入混凝土样本中。首先将最大的骨料放置在样品中,然后通过对Fuller曲线 进行采样来计算骨料的大小,其中d 是骨料的公称直径;da 是最大骨料的公称直径;n 是Fuller曲线指数。选择最小公称直径d0 作为定义模型分辨率的下限阈值。按照此步骤,可以生成一个充满球形骨料粒子的狗骨式样本,如图1(a)所示。
进行采样来计算骨料的大小,其中d 是骨料的公称直径;da 是最大骨料的公称直径;n 是Fuller曲线指数。选择最小公称直径d0 作为定义模型分辨率的下限阈值。按照此步骤,可以生成一个充满球形骨料粒子的狗骨式样本,如图1(a)所示。
《图1》
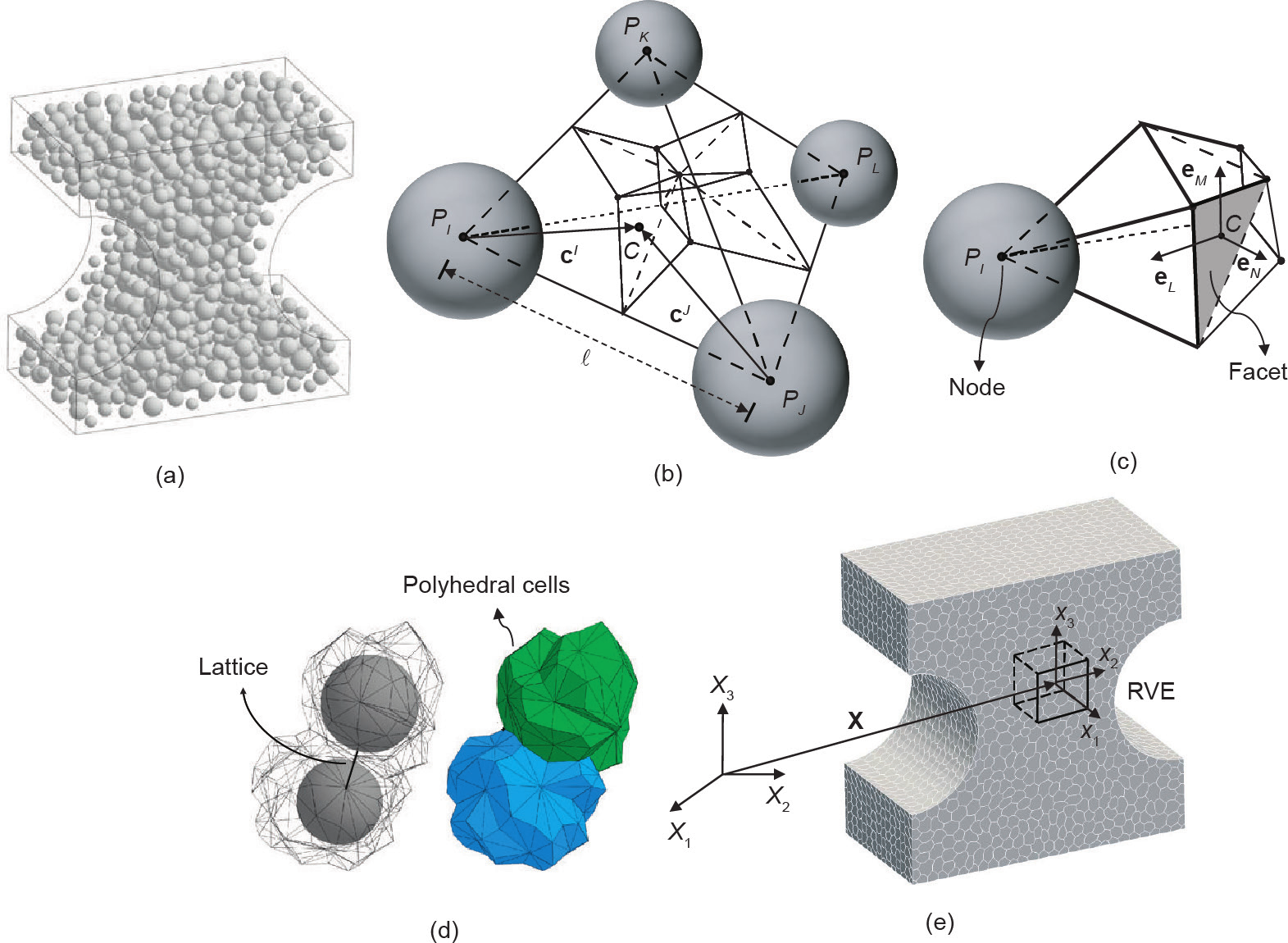
图1.(a)含有分散式球形骨料的狗骨式样本;(b)含有四个骨料粒子的通用LDPM四面体及其相关细分曲面;(c)与节点 有关的四面体部分;(d)围绕相关球形骨料的两个相邻LDPM多面体单元;(e)由多面体单元组成的狗骨式样本。
有关的四面体部分;(d)围绕相关球形骨料的两个相邻LDPM多面体单元;(e)由多面体单元组成的狗骨式样本。
(2)将半径为零的计算节点放置在这个样本的外表面上,这些是用于应用边界条件的实体。
(3)对生成的混凝土骨料的中心和外部节点执行Delaunay四面体化,以生成四面体系统。如图1(b)所示,这个四面体系统的3D细分曲面在每个四面体内部形成了一个三角形小平面网络。曲面细分的结果是,每个四面体元素被分为四个部分,每个部分与一个节点相连接。与通用节点相连接的细分子域相互组合形成了一个多面体单元,该单元包含该节点和相应的球形骨料。图1(c)显示了与节点 相关联的子域。三角形小平面是根据应变矢量到应力矢量定义的矢量本构方程的位置。这些小平面是可能在混凝土中形成裂纹和损坏的潜在平面,而且是两个相邻多面体单元相互作用的位置,如图1(d)所示。图1(e)显示了图1(a)中所示的狗骨式样本的多面体单元。值得注意的是,球形骨料仅用于构建类似于实际混凝土中尺度材料结构的几何形状,它们在数值求解过程中并不起作用。另外,在下文中被分别称为“节点”和“单元”的球形粒子的质心和相关的多面体单元是用于数值分析的几何实体。在本文中,单元和节点分别用
相关联的子域。三角形小平面是根据应变矢量到应力矢量定义的矢量本构方程的位置。这些小平面是可能在混凝土中形成裂纹和损坏的潜在平面,而且是两个相邻多面体单元相互作用的位置,如图1(d)所示。图1(e)显示了图1(a)中所示的狗骨式样本的多面体单元。值得注意的是,球形骨料仅用于构建类似于实际混凝土中尺度材料结构的几何形状,它们在数值求解过程中并不起作用。另外,在下文中被分别称为“节点”和“单元”的球形粒子的质心和相关的多面体单元是用于数值分析的几何实体。在本文中,单元和节点分别用 和
和 表示,其中I =1, …, N,N 为粒子总数。
表示,其中I =1, …, N,N 为粒子总数。
2.1.1. 小平面应变矢量定义
鉴于具有节点 和
和 [图1(b)]的两个相邻多面体单元之间共享的通用构面,位移跳跃矢量
[图1(b)]的两个相邻多面体单元之间共享的通用构面,位移跳跃矢量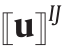 可以以描述单元系统变形的刚体运动学为基础,利用构面的质心来计算,然后将其用于定义小平面应变矢量,具体如下:
可以以描述单元系统变形的刚体运动学为基础,利用构面的质心来计算,然后将其用于定义小平面应变矢量,具体如下:

式中, α = N, M, L,如图1(c)所示。通过小位移、小旋转和小应变假设得到等式(1)中的小平面应变矢量公式。如等式(1)所示,在本文其余部分,上标IJ 只有在数量符号因I 和J 互换而发生改变时才需要被写出,如小平面法矢量或切矢量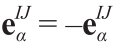 。如参考文献[24]所述,定义法线和切线方向的局部坐标系与正交于连接两个单元节点的晶格线投影的三角形小平面有关,与原始小平面的方向相反。值得一提的是,等式(1)中的应变矢量定义与连续微极性应变张量在空间的一般方向上的投影一致 [33]。
。如参考文献[24]所述,定义法线和切线方向的局部坐标系与正交于连接两个单元节点的晶格线投影的三角形小平面有关,与原始小平面的方向相反。值得一提的是,等式(1)中的应变矢量定义与连续微极性应变张量在空间的一般方向上的投影一致 [33]。
在等式(1)中,假定 α = N, M, L,ϵN 是小平面法向应变分量,ϵM 和ϵL 是小平面切向应变分量。如图1(b)所示,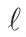 是两个相邻粒子
是两个相邻粒子 和
和 的中心距,可以根据
的中心距,可以根据
 来计算。
来计算。 是用于描述小平面局部Cartesian坐标系的单位矢量——
是用于描述小平面局部Cartesian坐标系的单位矢量—— 是正交于投影平面的单位矢量,那么
是正交于投影平面的单位矢量,那么 则是在与小平面相切方向上的单位矢量。将用来连接两个节点
则是在与小平面相切方向上的单位矢量。将用来连接两个节点 和
和 与小平面质心的矢量分别用
与小平面质心的矢量分别用 和
和 表示。对于所有这些几何实体,可以参考图1(b)和图1(c)。
表示。对于所有这些几何实体,可以参考图1(b)和图1(c)。 是节点
是节点 和
和 的位移矢量,而
的位移矢量,而 是节点
是节点 和
和 的旋转矢量。
的旋转矢量。
2.1.2. 小平面本构方程
利用每个小平面质心处所建立的本构方程来描述材料特性,并将小平面应变矢量与应力矢量相关联。LDPM本构方程简要概述如下,但读者可以参考先前的研究[24,34]以了解更多详细信息。为了模拟弹性行为,小平面法向应力分量和切应力分量与相应的小平面法向应变分量和切应变分量是成正比的。
为了模拟拉伸和剪切-拉伸状态(ϵN > 0)下的断裂,我们计算了有效应变ϵ = 和有效应力
和有效应力 , 用以将小平面上的法向应力和剪切应力定义为 tN =ϵN (t /ϵ), tM = αϵM (t /ϵ)和 tL = αϵL ( t /ϵ)。有效应力t 为增量弹性
, 用以将小平面上的法向应力和剪切应力定义为 tN =ϵN (t /ϵ), tM = αϵM (t /ϵ)和 tL = αϵL ( t /ϵ)。有效应力t 为增量弹性 , 并且受不等式0 ≤ t ≤ σbt (ϵ, ω )的限制。应力边界为 σbt = σ0( ω )exp[– H0 (ω ) 〈ϵmax – ϵ0( ω )〉/ σ0( ω )],其中〈x 〉= max{x , 0}, σ0( ω ) =σ0( ω )/ E0 ;并且 tanω =
, 并且受不等式0 ≤ t ≤ σbt (ϵ, ω )的限制。应力边界为 σbt = σ0( ω )exp[– H0 (ω ) 〈ϵmax – ϵ0( ω )〉/ σ0( ω )],其中〈x 〉= max{x , 0}, σ0( ω ) =σ0( ω )/ E0 ;并且 tanω =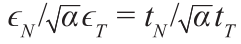 , 其中ϵmax =
, 其中ϵmax =  ,
,  。 ω 是控制法向载荷和剪切载荷之间耦合程度的参数。
。 ω 是控制法向载荷和剪切载荷之间耦合程度的参数。 是小平面承受的最大有效应变,即没有卸载时,ϵmax = ϵ。峰后行为的软化模量
是小平面承受的最大有效应变,即没有卸载时,ϵmax = ϵ。峰后行为的软化模量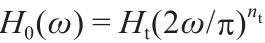 , 其中nt 是软化指数,Ht 是纯拉伸(当 ω = π/2时)状态下的软化模量,所得公式为
, 其中nt 是软化指数,Ht 是纯拉伸(当 ω = π/2时)状态下的软化模量,所得公式为 。
。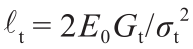 是拉伸特征长度,Gt 是中尺度断裂能。纯剪切力( ω = 0)到纯拉伸力之间的过渡是一个平滑函数,该函数的强度以抛物线
是拉伸特征长度,Gt 是中尺度断裂能。纯剪切力( ω = 0)到纯拉伸力之间的过渡是一个平滑函数,该函数的强度以抛物线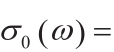


 形式变化,其中rst= σs/σt 是剪切拉伸强度比。
形式变化,其中rst= σs/σt 是剪切拉伸强度比。
相反,当小平面处于压缩状态(ϵN < 0)下时,在考虑不等式–σbc (ϵD , ϵV ) ≤ tN =E0ϵN ≤ 0的情况下计算法向应力,其中 σbc 取决于四面体元素体积应变的边界应力函数ϵV,小平面偏斜应变ϵD=ϵN –ϵV 。由四面体元素的体积变化来计算体积应变,ϵV = ΔV /3V0 ,对于所有属于该四面体元素的小平面,该体积应变是相等的。函数σbc (ϵD , ϵV )描述了高约束下的孔塌陷和再硬化,其定义如下:对于–ϵV ≤ ϵc0 = σc0 / E0,σbc =σc0 ;对于ϵc0≤ –ϵV ≤ ϵc1 = κc0ϵc0 ,Hc = Hc0 /(1+ κc2 〈 rDV – κc1 〉);对 于–ϵV ≥ ϵc1 ,σbc = σc1 ( rDV )exp[(–ϵV – ϵc1 ) Hc ( rDV )/σc1 ( rDV )],σc1 (rDV ) = σc0 + (ϵc1 – ϵc0 )Hc( rDV )。在前面的等式中,对于ϵV > 0, rDV = 10|ϵD|/ϵc0 ;对于ϵV < 0, rDV = –|ϵD|/(ϵV – 0.1ϵc0 );σc0 , Hc0 , κc0 , κc1 和 κc2 是材料参数。
对于受压面,剪切应力增量的计算公式为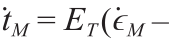
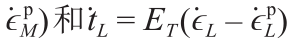 ,其中
,其中 ;λ 是塑性比例系数,其加载和卸载条件分别为
;λ 是塑性比例系数,其加载和卸载条件分别为 。本构模型屈服面和塑性势分别用
。本构模型屈服面和塑性势分别用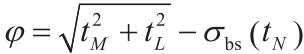 ,其中
,其中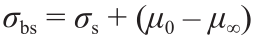
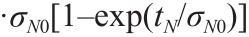
 和
和 表示。式中,
表示。式中,  是过渡法向应力; μ0 是初始内部摩擦系数; μ∞ 是最终内部摩擦系数。
是过渡法向应力; μ0 是初始内部摩擦系数; μ∞ 是最终内部摩擦系数。
2.1.3. 单元平衡方程
最后,通用LDPM单元C I 的平移和旋转平衡方程为:

式中, 是由单元
是由单元 组成的一系列小平面;A是投影面的面积;
组成的一系列小平面;A是投影面的面积; 是单元体积;
是单元体积; 是体力矢量,其在整个单元上被认为是均匀的;
是体力矢量,其在整个单元上被认为是均匀的; 作用在三角形小平面上的合成应力矢量。
作用在三角形小平面上的合成应力矢量。
LDPM是名为MARS的计算软件包的一部分[35],已被广泛用于模拟混凝土的力学行为[25]。此外,LDPM在动态条件下的混凝土响应模拟[36,37]、钢[34]纤维增强聚合物(FRP)混凝土断裂建模、纤维增强混凝土模拟[38,39]以及混凝土穿孔响应[40]等方面都取得了巨大成功。
《2.2. ASR 控制方程》
2.2. ASR 控制方程
在过去的几十年中,研究人员广泛地研究了ASR发展进程中的化学和物理过程。结果表明,这些变化过程很大程度上取决于骨料的矿物学和化学性质、水泥的组成、水泥的替代产品及其他添加剂。此外,据报道,二氧化硅没有均匀地分布在每个骨料片上。相反,它以离散的包裹体、囊袋和脉络状的形式出现[41,42]。水泥浆[43,44]中存在的各种碱金属离子,如Na+ 、K+ 和Ca2+ ,在氢氧根离子(OH- )和水(H2O)的存在下与骨料中的二氧化硅发生反应[45–47],这些反应主要发生在混凝土寿命的后期[48,49]。ASR会产生无定形的膨胀凝胶,由于骨料的不同矿物性质和有效的碱金属离子,这些凝胶的化学成分差异很大[50,51]。此外,研究人员表示ASR凝胶的流动性和膨胀特性主要取决于钙和水的含量[52–54],并且在后期还会发生进一步的化学反应[55]。ASR凝胶具有显著的膨胀特性,可导致骨料和水泥浆的明显开裂和损坏[56,57]。实验结果清楚地证明了ASR凝胶的存在,特别是在骨料的外表面、骨料内部和活性很强的骨料裂纹内部。值得注意的是,这并不能说明凝胶是流动的,因为这可能与裂纹促进水和金属离子的运输有关,从而使裂纹内部产生更多的凝胶[52,53,58]。
然而,在ASR期间,水泥浆中碱金属离子必须要渗透到骨料才能发生反应并形成ASR凝胶。此外,必须给凝胶提供额外的水分,以使其吸收水分并随后膨胀。前文清楚地表明,中尺度扩散过程一定会发生。因此,在先前的研究中,我们选择了一个中尺度混凝土模型,该模型可以捕获ASR的主要现象和平均次尺度现象[23]。在此方法中,依赖于碱性凝胶形成和吸水性的单个骨料的总体平均膨胀率被转换为不均匀的凝胶应变,并作为特征应变被应用于LDPM框架内的混凝土中尺度结构。ASR-LDPM最初是为满足饱和条件和均匀碱浓度而配制的 [23],最近它已被推广用于可变环境条件和可变碱金属离子浓度的情况[26]。
如前所述,为了生成ASR凝胶,碱金属离子和水必须扩散至整个骨料,并与骨料中的二氧化硅接触。因此,可以通过求解骨料径向扩散过程的稳态质量平衡,计算出直径为d 的一般骨料周围的凝胶质量Mg 。图2(a)和图2(b)展示了ASR期间的扩散过程,其中z是根据骨料中心计算出的扩散前沿位置,其值等于骨料未反应部分的半径。因此,ASR凝胶质量Mg 计算如下:

式中,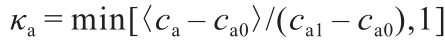 , 代表了水泥浆中碱含量水平的参数;
, 代表了水泥浆中碱含量水平的参数; 是碱含量下限,此时没有发现ASR膨胀;
是碱含量下限,此时没有发现ASR膨胀; 是足以完成ASR的饱和碱含量;
是足以完成ASR的饱和碱含量; 是硅胶转化的自由参数。ASR扩散前沿的速度可用下式表示:
是硅胶转化的自由参数。ASR扩散前沿的速度可用下式表示:
《图2》
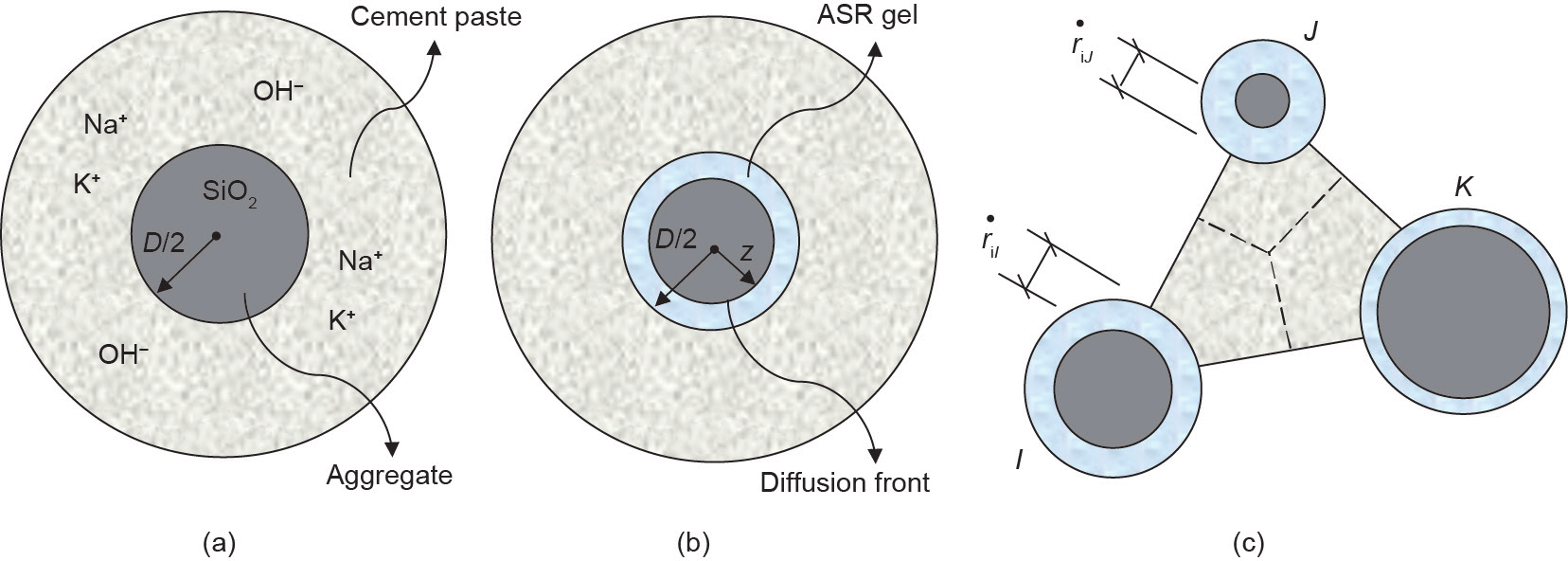
图2.(a)通用骨料及其周围的水泥浆; (b)在通用骨料周围形成的ASR凝胶; (c)在ASR效应下由2D模型中的三个骨料生成的三角形元素。

式中,T0 和T 分别是参考温度和当前温度;Eag 是扩散过程的活化能;R 是摩尔气体常数;ww 是骨料周围水泥浆中的含水量密度,在饱和情况下可利用公式 ww =c ( w/c – 进行估算[59]。其中
进行估算[59]。其中 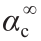 = (1.031 w/c )/(0.194 + w/c )是渐近水合度;
= (1.031 w/c )/(0.194 + w/c )是渐近水合度; 是在室温(296 K)下富碱水对骨料的渗透率。
是在室温(296 K)下富碱水对骨料的渗透率。
ASR凝胶一旦形成就会吸收水分并发生膨胀,从而向周围材料施加膨胀压力,导致材料损坏和破裂。吸水过程是根据参考文献[26]中介绍的演变规律制定的:

式中,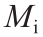 是吸收的水的质量;
是吸收的水的质量; 是最大吸水量与凝胶质量的比;
是最大吸水量与凝胶质量的比; 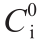 是骨料表面周围的水的初始微扩散率;δ 是水从骨料周围的混凝土流到ASR凝胶的有效距离。指数项则反映了这样一个事实,即随着吸水过程的进行,ASR凝胶的扩散率降低。最后,吸水过程的温度依赖性用以吸水过程活化能Eai 表示的Arrhenius-type方程的形式表示。
是骨料表面周围的水的初始微扩散率;δ 是水从骨料周围的混凝土流到ASR凝胶的有效距离。指数项则反映了这样一个事实,即随着吸水过程的进行,ASR凝胶的扩散率降低。最后,吸水过程的温度依赖性用以吸水过程活化能Eai 表示的Arrhenius-type方程的形式表示。
通过计算吸收的水的质量,可以知道相应骨料的平均膨胀程度,其半径为

式中,括号〈〉提取了封闭表达式的正值。在等式(6)中, 代表的是与凝胶膨胀相关的吸收的水,它存在于界面过渡区(ITZ)的孔隙中而不会产生任何压力;r = D/2是骨料的初始半径;δc 表示ITZ中孔隙的可用空间;ρw 是水的质量密度。
代表的是与凝胶膨胀相关的吸收的水,它存在于界面过渡区(ITZ)的孔隙中而不会产生任何压力;r = D/2是骨料的初始半径;δc 表示ITZ中孔隙的可用空间;ρw 是水的质量密度。
根据等式(6),通用骨料半径的时间变化率可用下式表示:

因此,由LDPM晶格中通用小平面上的ASR凝胶膨胀产生的正常本征应变时间变化率 用下式表示:
用下式表示:

式中, 是骨料
是骨料 的半径的时间变化率,它们共用一个小平面,如图2(c)所示。
的半径的时间变化率,它们共用一个小平面,如图2(c)所示。
值得注意的是,由ASR凝胶膨胀产生的剪切本征应变被假定为零,即 ,但由于真实的骨料的形状不规则,所以这仅仅是实际情况的一个近似值。
,但由于真实的骨料的形状不规则,所以这仅仅是实际情况的一个近似值。
《3. 多尺度均质化方法》
3. 多尺度均质化方法
本研究采用参考文献[30]所提出的均质化技术来计算由ASR效应引起的LDPM RVE的平均力学响应。利用该平均力学响应进行了标准有限元计算,计算过程考虑了中尺度混凝土异质性的影响。
参照图3,我们在宏观尺度上考虑了X和x两个坐标系,它们分别代表了用于确定RVE中位置的全局宏观坐标系和局部坐标系,如图1(e)所示。另外,我们还考虑了中尺度坐标系y,解决了材料异质性问题。在X和x中,假定材料域是同质的,在此范围内材料异质性是显示不出来的。根据尺度分离假设[60,61],当η 是一个小的正标量时,关系式x = ηy成立,0 < η ≤ 1。值得注意的是,在图1(e)中,为了清楚地表示两尺度问题,我们在视觉上违背了尺度分离假设。
《图3》

图3. 两尺度均质化方案。(a)宏观材料域; (b)包含材料异质性的中尺度域; (c)两个相邻的多面体单元。
我们考虑了两个独立的场变量u(x, y)和Θ(x, y),这两个场变量分别代表通用计算节点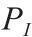 的位移矢量和旋转矢量。这些变量是宏观尺度和中尺度坐标系的函数,当评估
的位移矢量和旋转矢量。这些变量是宏观尺度和中尺度坐标系的函数,当评估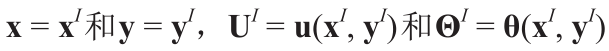 时,它们对应于中尺度自由度(DOFs)。这些变量可以在两个单独的尺度上进行如下扩展:
时,它们对应于中尺度自由度(DOFs)。这些变量可以在两个单独的尺度上进行如下扩展:

式中, 分别是宏观尺度和小尺度位移场,它们在x中是连续的,在y中是不连续的。此外,由于旋转矢量可以通过旋度算符与位移矢量相关联,因此用ω0和ω1 可以直接表明小尺度旋转矢量,而φ0 和φ1 是宏观旋转场 [30]。
分别是宏观尺度和小尺度位移场,它们在x中是连续的,在y中是不连续的。此外,由于旋转矢量可以通过旋度算符与位移矢量相关联,因此用ω0和ω1 可以直接表明小尺度旋转矢量,而φ0 和φ1 是宏观旋转场 [30]。
使用等式(1)中位移和旋转矢量的渐近展开式,考虑到小尺度RVE的刚体运动[30],LDPM小平面应变的渐近表达式如下:
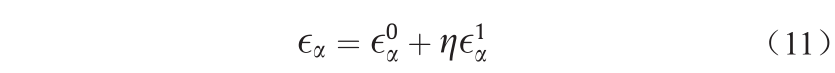
忽略宏观曲率效应,可以获得以下结果:
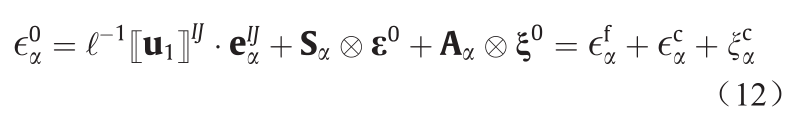
零阶的小平面应变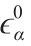 由三项组成:第一项是
由三项组成:第一项是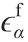 ,对应等式(1)的小尺度的小平面应变;第二项是
,对应等式(1)的小尺度的小平面应变;第二项是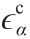 ,对应对称宏观应变张量
,对应对称宏观应变张量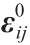 的投影
的投影 ;第三项是
;第三项是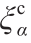 ,对应反对称宏观应变张量
,对应反对称宏观应变张量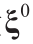 的投影
的投影 。张量
。张量 是Levi-Civita排列符号。
是Levi-Civita排列符号。 是投影算子,可被推导为
是投影算子,可被推导为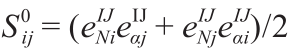 和
和 。本质上,等式(12)中的第二和第三项表示了应如何将每个有限元积分点处的宏观应变张量投影到相应的LDPM RVE面上,以解决RVE问题。有关该理论的详细推导,请见参考文献[30]。
。本质上,等式(12)中的第二和第三项表示了应如何将每个有限元积分点处的宏观应变张量投影到相应的LDPM RVE面上,以解决RVE问题。有关该理论的详细推导,请见参考文献[30]。
LDPM小平面应力的渐近展开式可通过使用小平面应变的渐近形式得出;利用该结果与等式(2)可推导出两个独立尺度的平移和旋转平衡方程——零阶是RVE问题,一阶是宏观或粗尺度问题。
RVE平移和旋转平衡方程如下:

式中,零阶小平面应力 是使用第2.1节中给出的本构方程并根据零阶小平面应变
是使用第2.1节中给出的本构方程并根据零阶小平面应变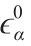 计算得出的。等式(12)可被改写为
计算得出的。等式(12)可被改写为 ,这意味着宏观应变张量的投影是以阐述RVE问题的小平面本征应变的形式被应用的。通过使用周期边界条件求解RVE平衡方程,可以得到零阶牵引力
,这意味着宏观应变张量的投影是以阐述RVE问题的小平面本征应变的形式被应用的。通过使用周期边界条件求解RVE平衡方程,可以得到零阶牵引力  。然后将其用于计算宏观对称和反对称应力张量,具体计算公式如下:
。然后将其用于计算宏观对称和反对称应力张量,具体计算公式如下:

式中,V 0 是RVE的体积。均质化理论还提供了宏观耦合应力张量,但由于其已被忽略[62],因此这里没有对它进行探讨。
最后,可以通过对一级平衡方程[30]进行平均来获得宏观平衡方程,具体如下:

如前所述,由于应力张量和耦合应力张量的反对称部分为零,因此应变张量的反对称部分也必须为零,即 。这使得在没有宏观旋转DOF和基于位移的标准有限元的情况下,基于LDPM的均质化框架的数值实现能够完成。
。这使得在没有宏观旋转DOF和基于位移的标准有限元的情况下,基于LDPM的均质化框架的数值实现能够完成。
图4是显示了本研究所采用的均质化框架,其中包括按照以下步骤进行的中尺度ASR效应:
《图4》
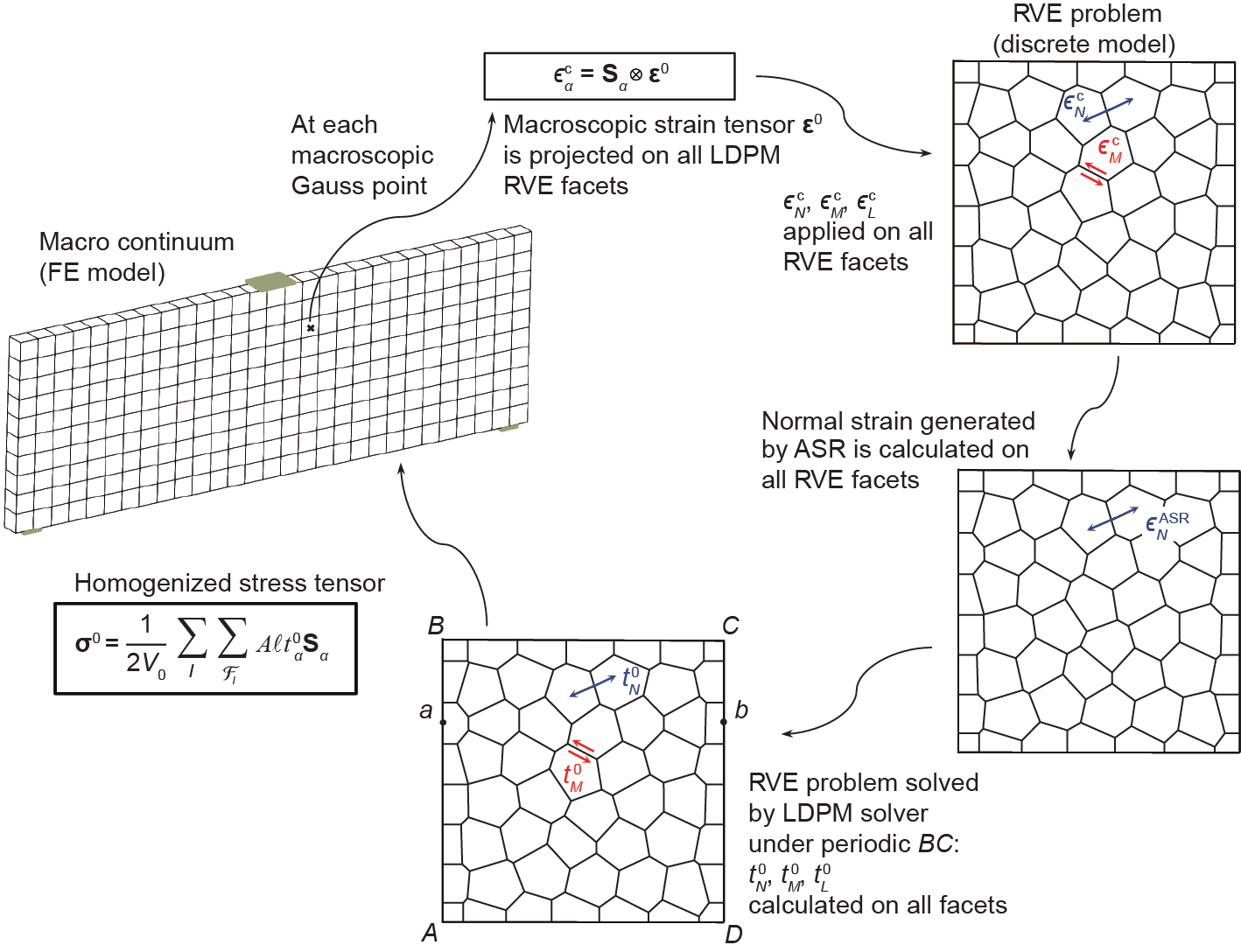
图4. 具有ASR效应的多尺度均质化方法的一般框架。FE:有限元。
(1)采用有限元法对宏观材料域进行离散化,并且将LDPM RVE分配给每个宏观有限元Gauss点。
(2)对于每个宏观加载步骤,在所有宏观有限元的每个Gauss点处计算宏观应变张量的增量 。
。
(3)在每个有限元Gauss点,使用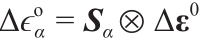 [等式(12)]将计算的宏观应变张量增量
[等式(12)]将计算的宏观应变张量增量 投影到所有相应的LDPM RVE小平面上。
投影到所有相应的LDPM RVE小平面上。
(4)计算每个LDPM RVE内部所有小平面由ASR产生的正应变增量 。
。
(5)RVE问题是通过在RVE上施加周期性边界条件,将 应用到所有RVE小平面上而得到解决的。将ASR产生的正应变以及预计的宏观应变作为本征应变应用于所有RVE面上,从而计算出受LDPM本构方程控制的小尺度解,即
应用到所有RVE小平面上而得到解决的。将ASR产生的正应变以及预计的宏观应变作为本征应变应用于所有RVE面上,从而计算出受LDPM本构方程控制的小尺度解,即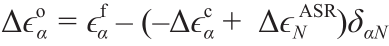 。其中,如果α = N,则δαN = 1;如果α = M或L,则δαN =0。然后计算所有RVE粒子的中尺度位移u1 和旋转矢量ω1 以及所有RVE小平面的牵引矢量
。其中,如果α = N,则δαN = 1;如果α = M或L,则δαN =0。然后计算所有RVE粒子的中尺度位移u1 和旋转矢量ω1 以及所有RVE小平面的牵引矢量 。
。
(6)基于RVE问题的解决方案,使用等式(14)计算宏观应力张量。
(7)然后将RVE均质应力张量传递回相应的Gauss点,以更新有限元节点位移和力。
《4. 数值结果》
4. 数值结果
在本节中,我们研究了所开发的多尺度框架的性能,用以评估ASR对混凝土体积膨胀以及力学性能退化的影响。首先,ASR-LDPM参数是根据Shehata和Thomas[63]的实验报告数据进行校准的。他们研究了尺寸为75 mm×75 mm×265 mm的密封混凝土棱柱体在320 d内的自由膨胀。他们采用了五个不同水平的碱含量(ca= 2.89 kg·m−3 、3.15 kg·m−3 、3.90 kg·m−3 、4.20 kg·m−3 和5.25 kg·m−3 )。实验中所使用的混凝土骨料粒度分布情况如下:三分之一的骨料的粒度在4.75~9.5 mm,另外三分之一的骨料的粒度在9.5~12.5 mm,最后三分之一的骨料的粒度在12.5~19 mm。对于LDPM样品的生成,使用以下参数:骨料最小直径d0 = 4.75 mm,骨料最大直径da =19 mm,Fuller曲线指数n = 0.55;配合比参数:水泥含量c = 420 kg·m−3 ,水灰比w/c = 0.45,骨灰比 = 4.25。为了校准ASR-LDPM参数,我们利用LDPM完全模拟了混凝土棱柱体,并研究了其随时间的体积膨胀。LDPM棱柱体的单元表示如图5(a)所示。针对每种碱含量水平,使用三种不同的LDPM粒子实现方法对棱柱体进行完整的LDPM分析,以研究RVE晶格的划分效果,并计算其平均特性。实验体积应变随时间的变化情况以及相应的多尺寸LDPM分析结果如图5(b)所示。可以看出,数值模拟结果与实验数据吻合良好。显然,随着ASR的持续进行,体积应变率会降低并达到平稳。应当注意的是,我们首先针对碱含量水平为2.89 kg·m−3 的棱柱体进行了ASR-LDPM参数校准,然后将其用于验证模型对其他碱含量水平的响应。被校准的ASR参数:
= 4.25。为了校准ASR-LDPM参数,我们利用LDPM完全模拟了混凝土棱柱体,并研究了其随时间的体积膨胀。LDPM棱柱体的单元表示如图5(a)所示。针对每种碱含量水平,使用三种不同的LDPM粒子实现方法对棱柱体进行完整的LDPM分析,以研究RVE晶格的划分效果,并计算其平均特性。实验体积应变随时间的变化情况以及相应的多尺寸LDPM分析结果如图5(b)所示。可以看出,数值模拟结果与实验数据吻合良好。显然,随着ASR的持续进行,体积应变率会降低并达到平稳。应当注意的是,我们首先针对碱含量水平为2.89 kg·m−3 的棱柱体进行了ASR-LDPM参数校准,然后将其用于验证模型对其他碱含量水平的响应。被校准的ASR参数: 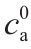 = 2.7 kg·m−3 ,
= 2.7 kg·m−3 ,  = 4.37 kg·m−3 ,
= 4.37 kg·m−3 ,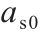 = 3.45×10−13 m2 ·s−1 ,
= 3.45×10−13 m2 ·s−1 ,  = 2.8×10−10 m2 ·s−1 ,ξ =439 540 kg−1 ,kg = 689 kg·m−3 ,Eag = Ead = 500 J·mol−1 ,δc= 1。参考温度T0 与当前温度T 相等,这意味着可以忽略温度的影响。应该注意的是,样品是密封的,并且保持接近100%的高相对湿度。模拟中使用的LDPM参数:EN =60 GPa,σt = 4.75 MPa,σc0 = 150 MPa,α = 0.25,nt = 0.2,
= 2.8×10−10 m2 ·s−1 ,ξ =439 540 kg−1 ,kg = 689 kg·m−3 ,Eag = Ead = 500 J·mol−1 ,δc= 1。参考温度T0 与当前温度T 相等,这意味着可以忽略温度的影响。应该注意的是,样品是密封的,并且保持接近100%的高相对湿度。模拟中使用的LDPM参数:EN =60 GPa,σt = 4.75 MPa,σc0 = 150 MPa,α = 0.25,nt = 0.2, = 75 mm,rst = 2.6,Hc0 /E0 = 0.4,μ0 = 0.4,μ∞ = 0,κc1 =1,κc2 = 5,σN0 = 600 MPa。因为参考文献[63]未提及力学性能,所以这些参数已针对标准混凝土的力学性能进行了校准[23]。
= 75 mm,rst = 2.6,Hc0 /E0 = 0.4,μ0 = 0.4,μ∞ = 0,κc1 =1,κc2 = 5,σN0 = 600 MPa。因为参考文献[63]未提及力学性能,所以这些参数已针对标准混凝土的力学性能进行了校准[23]。
《图5》
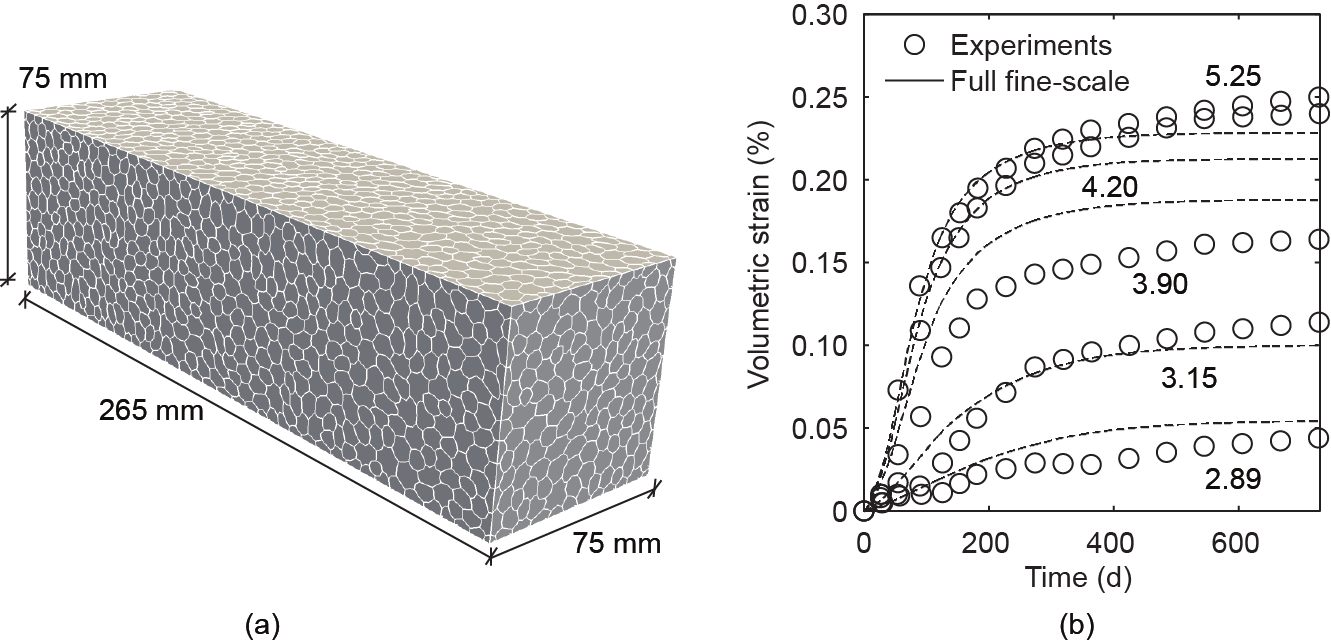
图5. (a)混凝土棱柱体的多面体单元表示; (b)通过完整的小尺度LDPM分析和实验获得的混凝土棱柱体的体积膨胀[图(b)中的纵坐标值为碱含量,单位为kg·m−3 ]。
由于小尺度的RVE是均质化框架的主要元素,因此,接下来的部分将首先研究LDPM RVE在拉伸和压缩条件下以及在ASR效应下的均质化反应。在参考文献[63]中,研究人员对混凝土棱柱体进行了研究,然后使用均质化方法进行建模并与小尺度仿真和实验数据进行比较,以确定多尺度框架的效率。但是,必须注意的是,本文的研究目的是检查多尺度框架的效率,从而以较低的计算成本准确地再现完整的LDPM分析结果,而不是针对实验数据进行验证。后一项研究工作已经在参考文献[23,27]中被提出。此外,本研究没有考虑在混凝土寿命期间发生的其他现象(如收缩和蠕变),尽管将它们纳入多尺度模型属于我们未来工作的范围。
《4.1. ASR 作用下 RVE 均质力学性能分析》
4.1. ASR 作用下 RVE 均质力学性能分析
在本节中,我们将使用上述配合比参数生成LDPM RVE。为了研究RVE尺寸的影响,我们采用了四种不同的RVE尺寸,分别为35 mm、50 mm、75 mm和100 mm。四种RVE尺寸的单元和粒子分布如图6和图7所示,对于每种RVE尺寸,我们采用了五种不同的粒子分布,以便检验RVE晶格划分效果。图8给出了75 mm LDPM RVE的五种不同的粒子分布。
《图6》

图6. 不同尺寸的RVE多面体单元表示。(a)35 mm; (b)50 mm; (c)75 mm; (d)100 mm。
《图7》
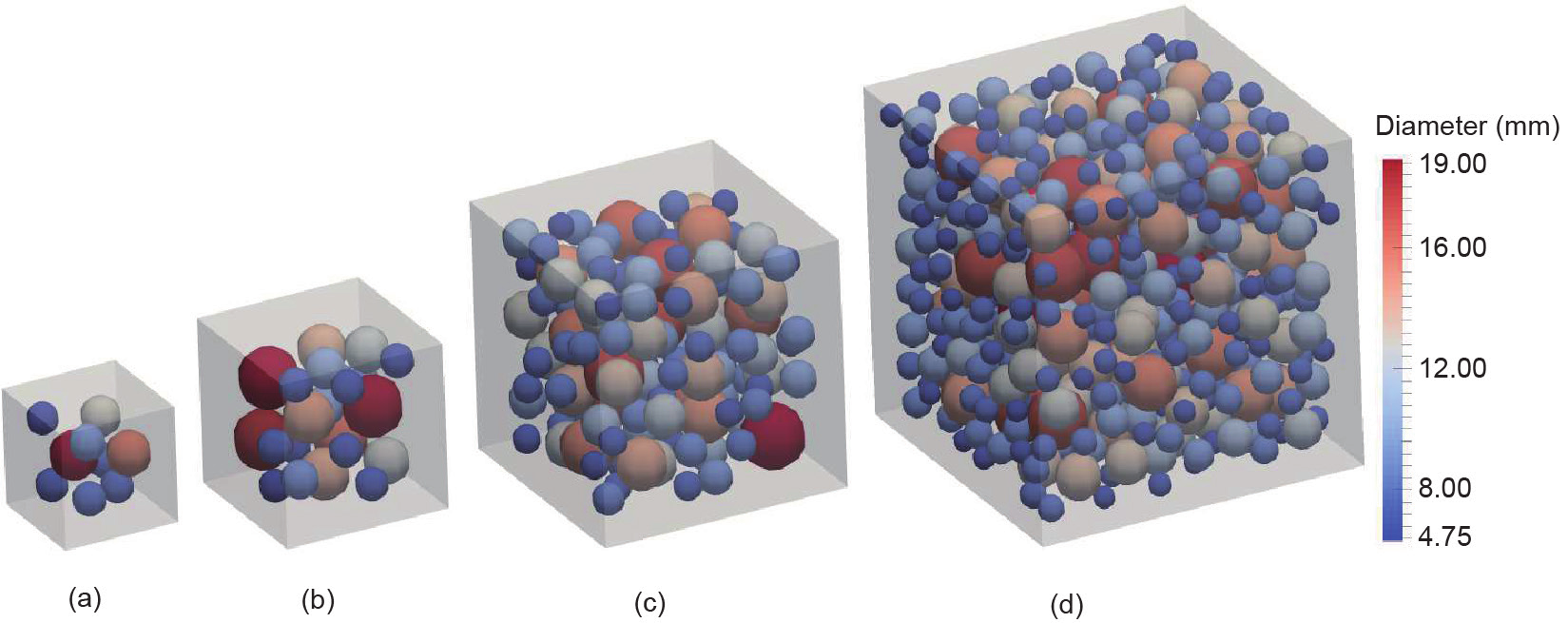
图7. 不同尺寸的RVE内部球形粒子分布。(a)35 mm; (b)50 mm; (c)75 mm; (d)100 mm。
《图8》

图8. 75 mm LDPM的RVE内部五种不同的粒子分布。
在ASR演变的三个不同阶段,我们测试了在单轴拉伸状态下生成的RVE。首先,在没有ASR效应的条件下对其进行测试。接下来,在ASR自由膨胀60 d和120 d后对RVE进行测试。我们使用第4节介绍的参数模拟了RVE的ASR膨胀,此时碱含量为2.89 kg·m−3 。样品在60 d和120 d时的ASR膨胀分别约为0.015%和0.025%。应当注意的是,对于所有四种不同尺寸的RVE,这些值大约相同。下一节介绍了RVE尺寸对自由膨胀曲线的影响及其与实验数据的比较。图9展示了ASR自由膨胀120 d后引起的RVE开裂轮廓。由此可知,ASR损伤在试样上是分散的,并且由此产生的裂纹是随机取向的,这符合在自由膨胀实验中所观察到的损伤模式。
《图9》
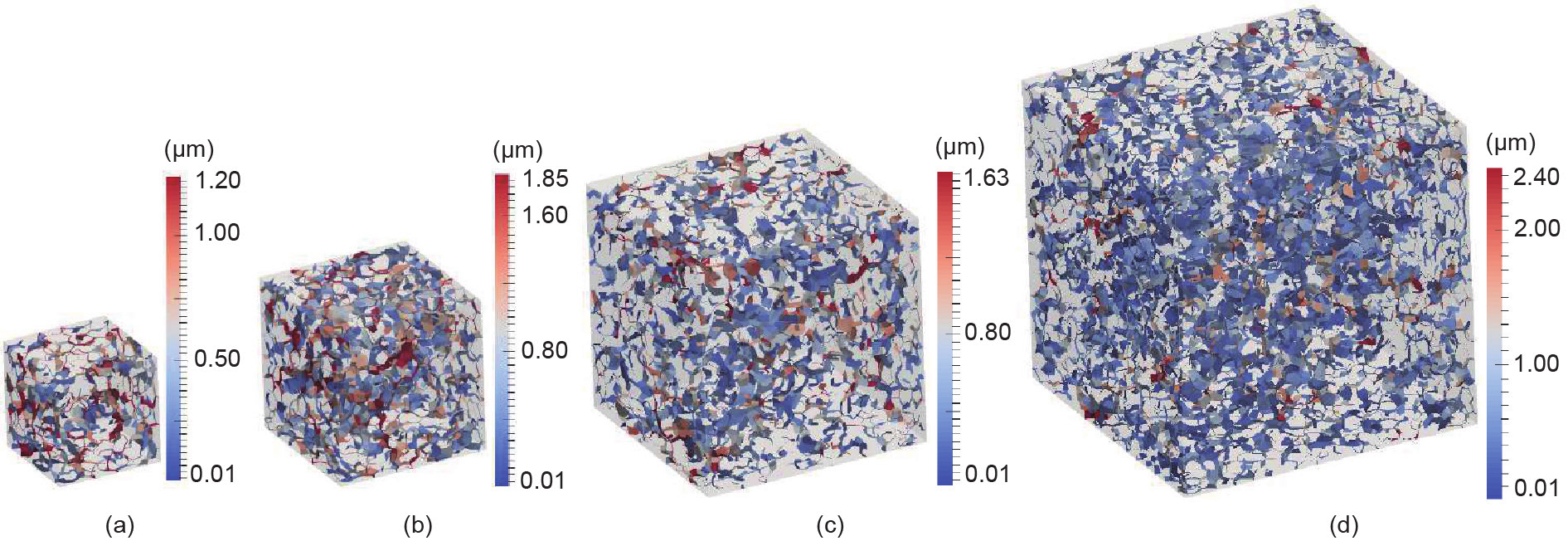
图9. 自由膨胀120天后,RVE的开裂轮廓。(a)35 mm; (b)50 mm; (c)75 mm; (d)100 mm。
在60 d和120 d时,我们对受损的RVE进行单轴拉伸,并将获得的应力-应变曲线与从无ASR损伤样品获得的应力-应变曲线进行比较。如图10所示,对每种RVE尺寸的不同粒子划分的拉伸应力-应变曲线取平均值。从每条曲线中计算出杨氏模量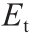 和拉伸峰值应力
和拉伸峰值应力  ,并将其与样品受ASR效应的时间作图,如图11所示。所有曲线沿时间轴略有偏移,以提供更清晰的误差线。由图11可知,每次计算得出的
,并将其与样品受ASR效应的时间作图,如图11所示。所有曲线沿时间轴略有偏移,以提供更清晰的误差线。由图11可知,每次计算得出的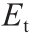 和
和  平均值都与不同的RVE尺寸匹配得非常好。因此,在RVE尺寸受影响最小的情况下,通过均质化方案,我们可以完美地捕捉到由ASR引起的混凝土杨氏模量和抗拉强度下降的情形。对于每种RVE尺寸,误差线显示了来自五个不同粒子划分的目标数量的标准偏差。正如所预期的那样,较小的RVE尺寸的标准偏差较高,这是因为RVE尺寸与骨料最大直径的比值较小。对于尺寸为100 mm的RVE,误差值可以忽略不计,这就意味着RVE内部的粒子分布对均质的量没有影响。这些结果清楚地表明,较小的RVE尺寸可用于多尺度均质化分析,以成功捕捉拉伸力学性能的下降趋势。
平均值都与不同的RVE尺寸匹配得非常好。因此,在RVE尺寸受影响最小的情况下,通过均质化方案,我们可以完美地捕捉到由ASR引起的混凝土杨氏模量和抗拉强度下降的情形。对于每种RVE尺寸,误差线显示了来自五个不同粒子划分的目标数量的标准偏差。正如所预期的那样,较小的RVE尺寸的标准偏差较高,这是因为RVE尺寸与骨料最大直径的比值较小。对于尺寸为100 mm的RVE,误差值可以忽略不计,这就意味着RVE内部的粒子分布对均质的量没有影响。这些结果清楚地表明,较小的RVE尺寸可用于多尺度均质化分析,以成功捕捉拉伸力学性能的下降趋势。
《图10》
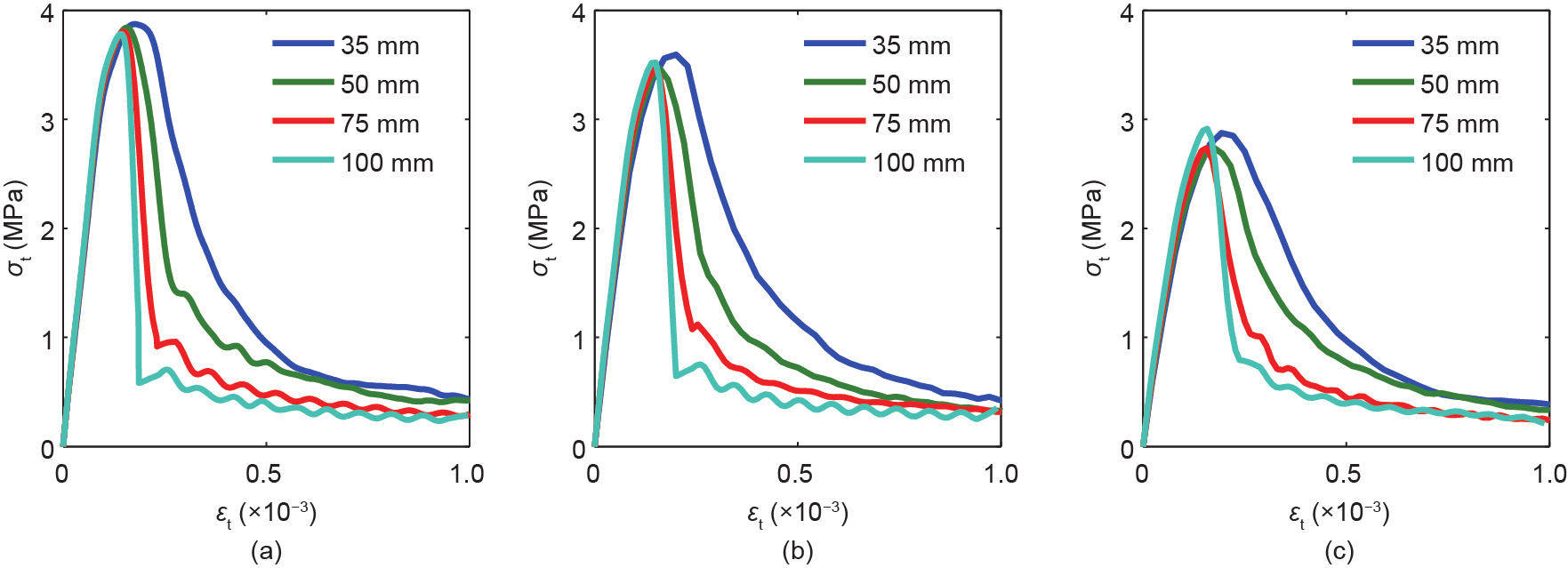
图10. 对于不同的RVE尺寸,在没有ASR演变(a)、在ASR演变的第60 d(b)以及在ASR演变的第120 d(c)时,在拉伸作用下的RVE非线性行为的平均曲线。
《图11》
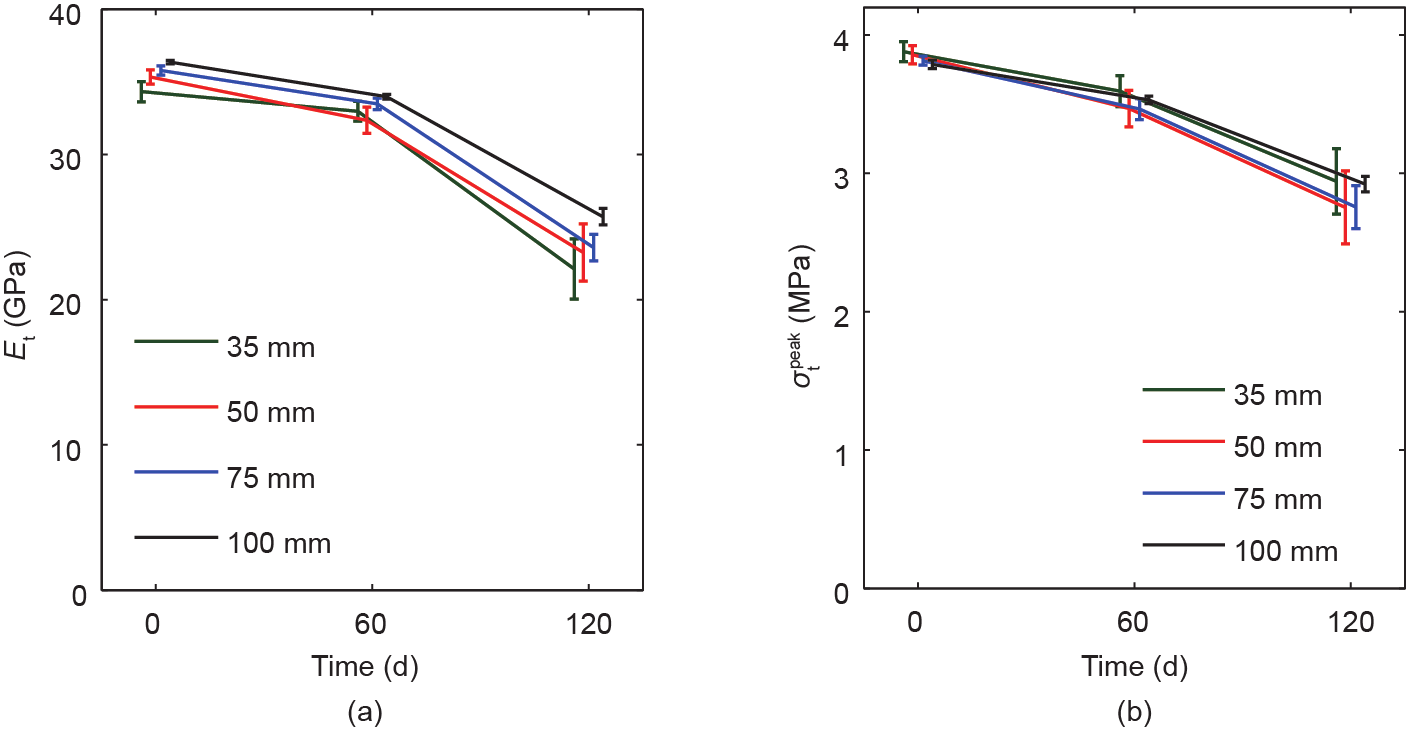
图11. 在 ASR引起的拉伸杨氏模量(a)和拉伸峰值应力(b)随时间的变化。
由图10可知,不同RVE尺寸下的不同峰后响应在准脆性材料(如混凝土)的断裂力学中被称为“尺寸效应”。这种效应是由拉伸作用下准脆性材料发生的局部损伤所引起的。同时,未损伤区域的弹性能将被释放。图12绘制了不同RVE尺寸的损伤区域图。“尺寸效应”是软化材料多尺度均质化中一个众所周知的问题,一般需要对软化材料进行特殊处理才能使多尺度框架正确地获取耗散的能量[64]。
《图12》
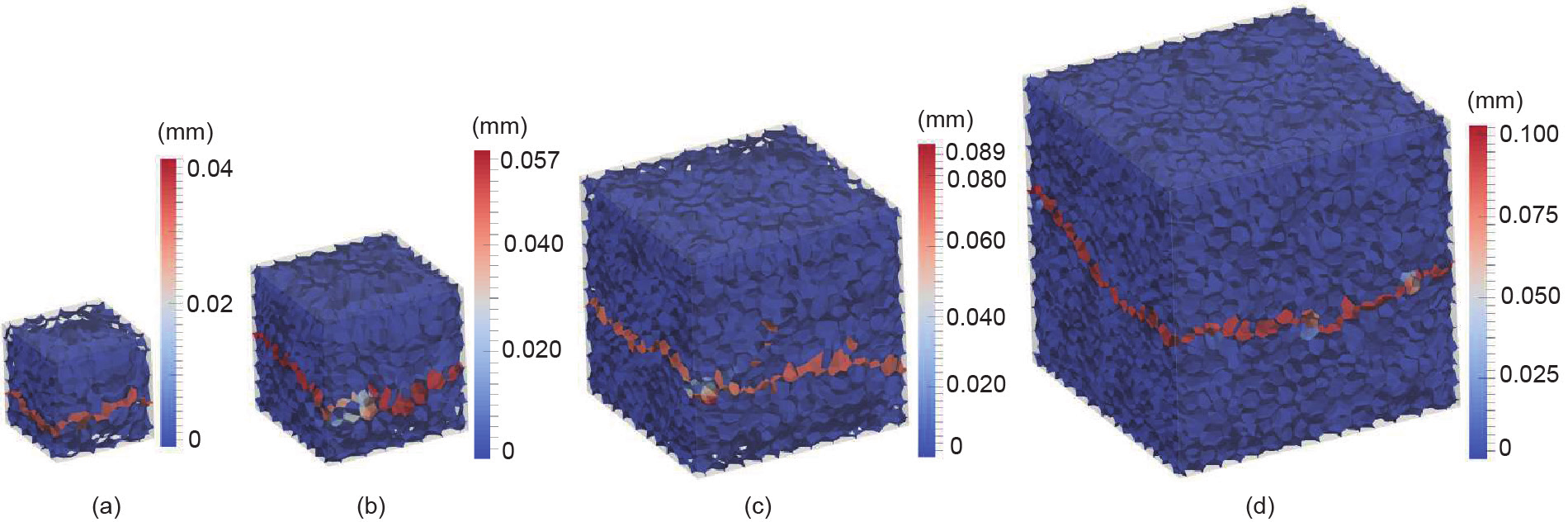
图12. 在轴向应变为1×10−3 的直接拉伸试验中的开裂轮廓。(a)35 mm; (b)50 mm; (c)75 mm; (d)100 mm。
接下来,在ASR演变两年零182 d后,通过对RVE进行单轴压缩试验,我们研究了由ASR引起的混凝土抗压强度和杨氏模量的演变过程。我们将REV的压缩响应与没有受到ASR效应的RVE的压缩响应进行比较。所有LDPM材料参数以及ASR参数都与上一节使用的参数一致。因为由ASR引起的混凝土抗压强度的降低不如抗拉强度降低[56]得明显,所以与前一节所述的相比,RVE的ASR演变周期更长。
我们对每种RVE尺寸根据不同粒子划分的压应力-应变曲线进行平均,并在图13中绘制了无ASR自由膨胀、ASR自由膨胀182 d以及ASR自由膨胀两年的压应力-应变曲线。图14显示了由ASR引起的杨氏模量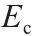 和压缩峰值应力
和压缩峰值应力  的变化,其中所有曲线沿时间轴略有偏移,用以提供清晰的误差线。由此可知,通过分析不同RVE尺寸所获得的
的变化,其中所有曲线沿时间轴略有偏移,用以提供清晰的误差线。由此可知,通过分析不同RVE尺寸所获得的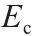 和
和  的均质化值在三个不同的时间段吻合得很好。因此,在保持结果准确性的前提下,较小的RVE尺寸可以用于多尺度均质化分析。与上一节类似,均质化的
的均质化值在三个不同的时间段吻合得很好。因此,在保持结果准确性的前提下,较小的RVE尺寸可以用于多尺度均质化分析。与上一节类似,均质化的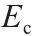 和
和  的标准偏差随RVE尺寸与骨料最大直径的比值的增加而减小。但是,即使是最小的RVE尺寸,这些量的标准偏差仍然可以忽略不计。应当指出的是,与拉伸行为相反,所有RVE尺寸在压缩下的峰后行为都吻合良好,如图13所示。这是由于单轴压缩下的RVE裂纹的分布很分散,并且在裂纹区域内没有局部性损伤,如图15所示。
的标准偏差随RVE尺寸与骨料最大直径的比值的增加而减小。但是,即使是最小的RVE尺寸,这些量的标准偏差仍然可以忽略不计。应当指出的是,与拉伸行为相反,所有RVE尺寸在压缩下的峰后行为都吻合良好,如图13所示。这是由于单轴压缩下的RVE裂纹的分布很分散,并且在裂纹区域内没有局部性损伤,如图15所示。
《图13》
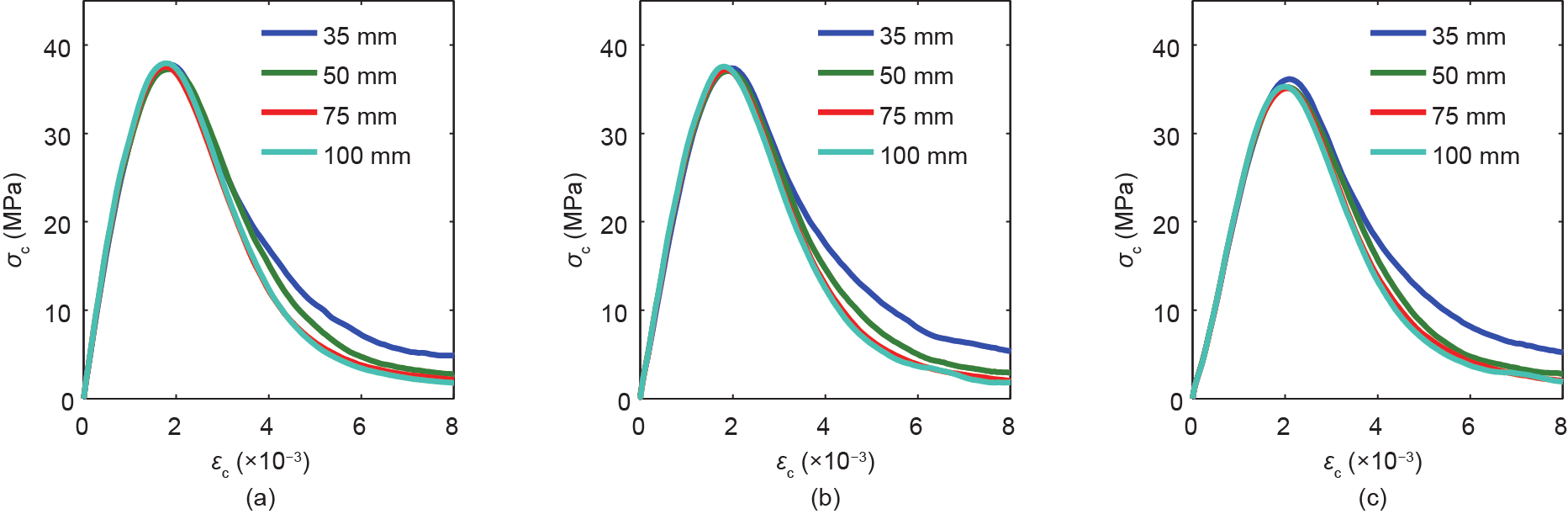
图13. 对于不同的RVE尺寸,在没有ASR演变(a)、在ASR演变182 d(b)以及在ASR演变两年(c)时,在拉伸作用下的RVE非线性行为的平均曲线。
《图14》
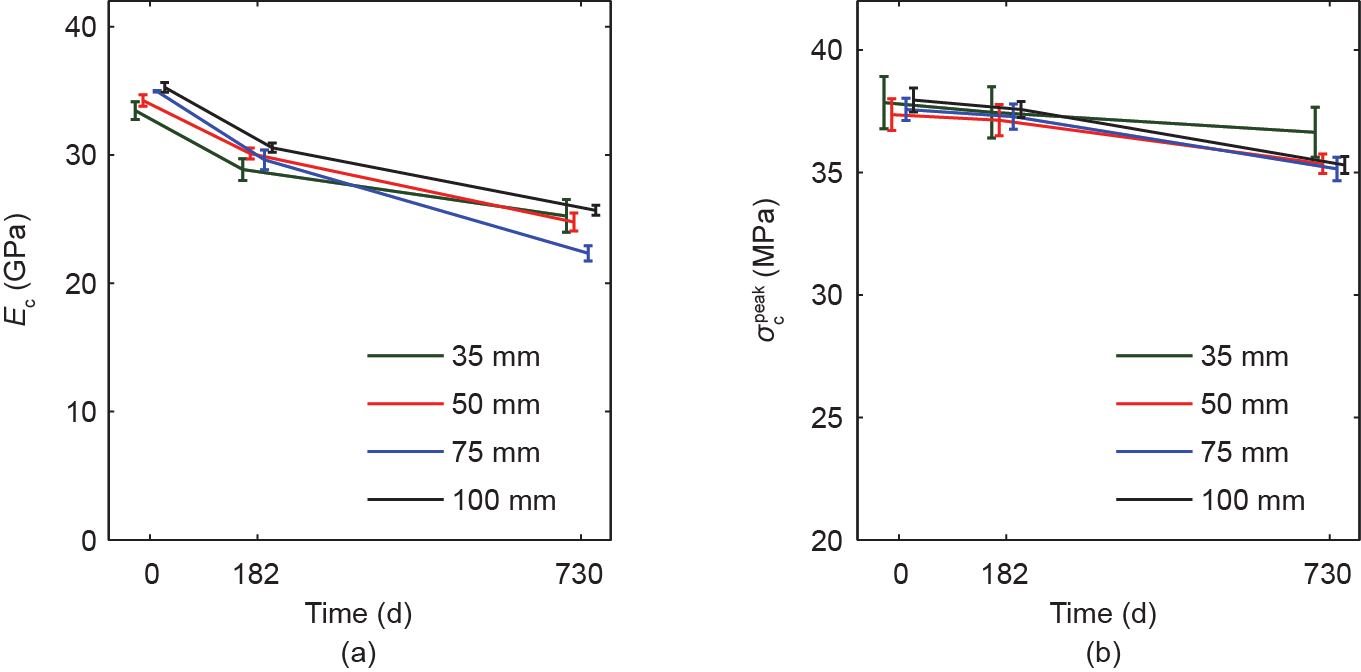
图14. 由ASR引起的压缩杨氏模量(a)和压缩峰值应力(b)随时间的变化。
《图15》
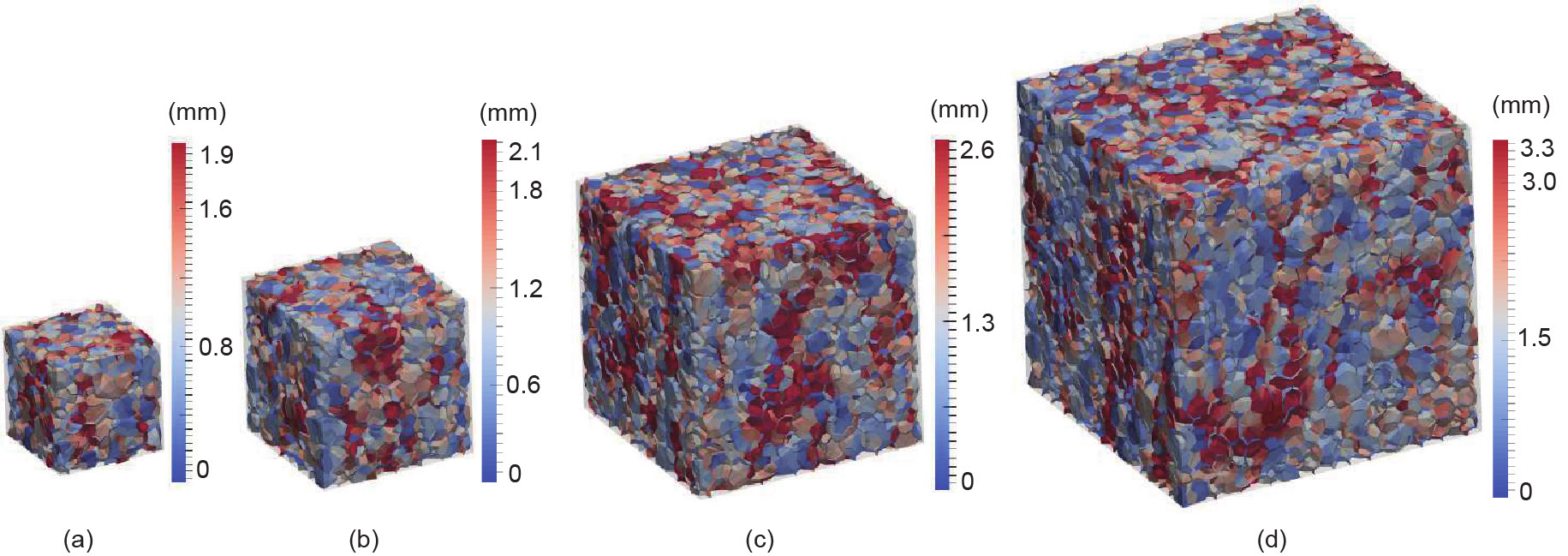
图15. 在轴向应变为8×10−3 的无限制压缩测试中的开裂轮廓。(a)35 mm; (b)50 mm; (c)75 mm; (d)100 mm。
《4.2. ASR 效应下的混凝土棱柱体两尺度均质化分析》
4.2. ASR 效应下的混凝土棱柱体两尺度均质化分析
在本节中,参考文献[63]和第4节研究了混凝土棱柱体,该棱柱体是通过完整的小尺度LDPM和两尺度均质化方法进行模拟的,用以研究多尺度模型再现完整的小尺度分析结果的能力。如图5(b)所示,针对棱柱体自由膨胀的实验记录进行校准的ASR-LDPM参数在这里被用于小尺度和多尺度均质化分析。在均质化分析中,我们利用边长为75 mm的三个单点积分六面体有限元对混凝土棱柱体离散化,如图16所示。为了研究RVE尺寸的影响,我们对35 mm、50 mm和75 mm三种不同的RVE尺寸进行了均质化分析,并将其分配给每个有限元的积分点。此外,针对每种RVE尺寸,我们对RVE内部的六种不同粒子划分方式进行了两尺度分析,以研究RVE内部粒子分布的影响。
《图16》
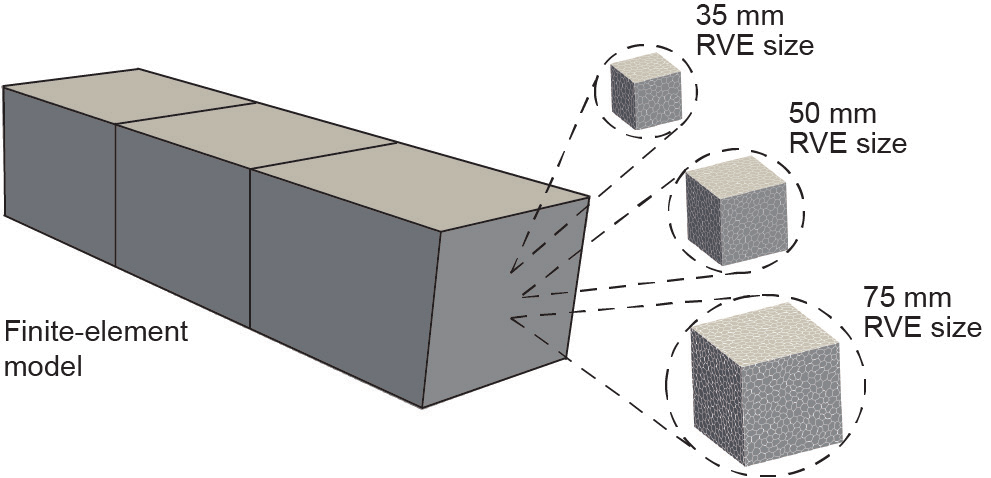
图16. 具有三个实体有限元和三种不同RVE尺寸的混凝土棱柱体的均质化模型
如图17 (a)~ (c),针对已分配的三种不同的RVE尺寸,我们绘制了通过两尺度均质化分析获得的混凝土棱柱体的体积膨胀与时间的关系图。根据实验报告,参考文献 [63]对五个不同碱含量的棱柱体进行了自由膨胀分析。我们针对每种RVE尺寸和碱含量值分别绘制了六个不同的曲线,分别对应于RVE内部的六个不同的粒子分布。显然,如上一节所述,对于较小的RVE尺寸,混凝土棱柱体的体积膨胀曲线更加分散。因此,RVE尺寸与骨料最大直径的比值越大,均质化结果的标准差就越小。此外,由关系图可知,对于更高的碱含量水平,混凝土棱柱体的体积膨胀曲线则更分散,这是因为更高的碱含量水平将导致更高水平的ASR损伤,并使RVE内部损伤分布的不均匀性进一步加剧。
《图17》
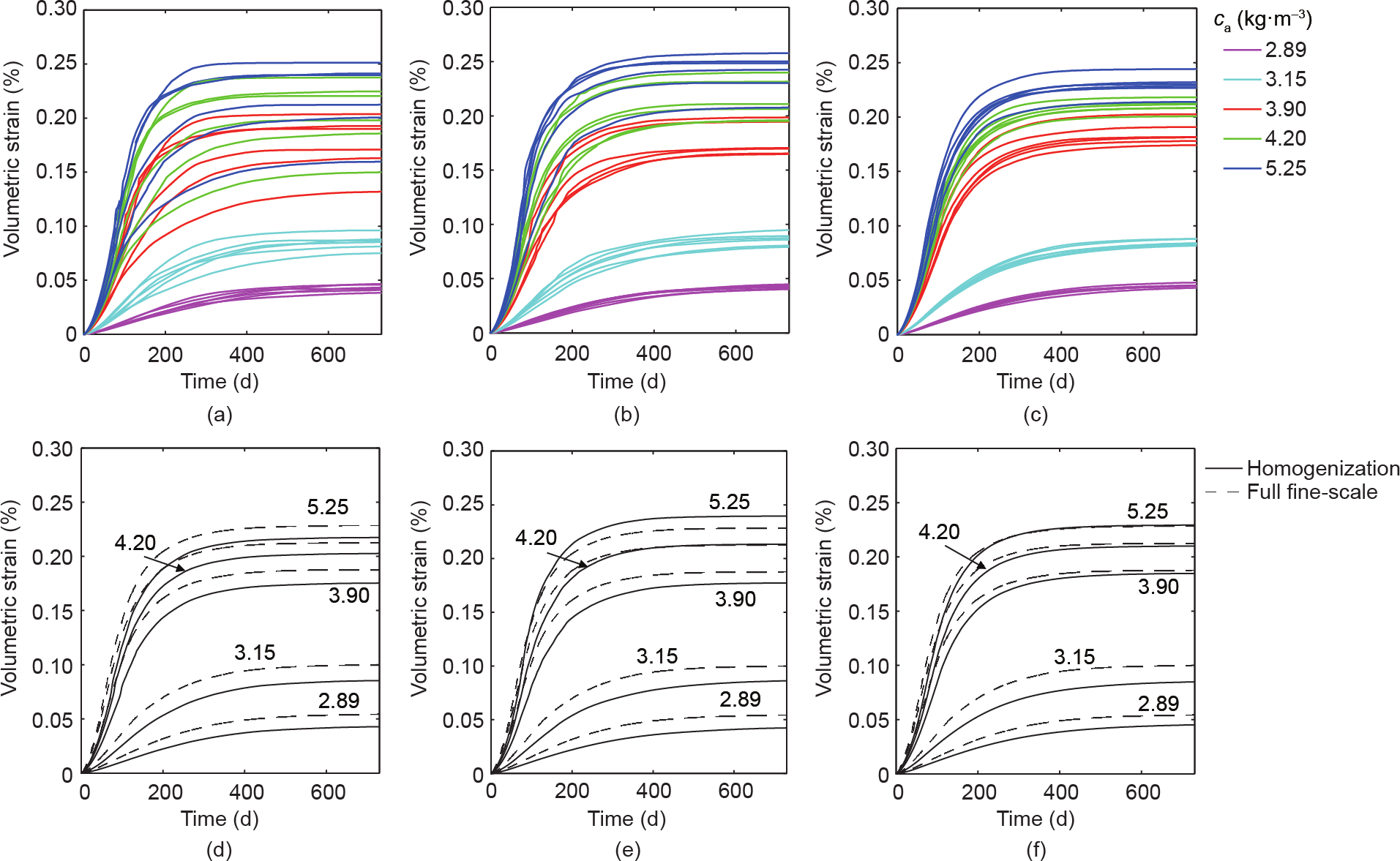
图17. RVE尺寸为35 mm(a)、50 mm (b)和75 mm(c)时,从均质化框架中获得的不同碱含量棱柱体的体积膨胀曲线;RVE尺寸为35 mm(d)、50 mm(e)和75 mm(f)时的均质化结果与完整的小尺度均质化结果的比较[图(d)~(f)中的纵坐标值是碱含量,单位为kg·m−3 ]。
我们针对每种RVE尺寸和不同碱含量条件下形成的曲线进行平均化,并与图17(d)~(f)中完整的小尺度LDPM分析结果进行比较。可以看出,对于不同的RVE尺寸和不同的碱含量,均质化结果和完整的小尺度分析结果非常匹配。随着RVE尺寸的增加,均质化结果与完整的小尺度模拟更加接近。由于较大尺寸的RVE能更好地代表经过均质处理的低尺度材料结构,因此这样的结果是在预料之中的。
接下来,为了研究多尺度均质化方法在捕捉混凝土抗压强度退化方面的能力(与完整小尺度LDPM分析方法相比),我们对相同棱柱体在不同ASR演变周期后进行单轴压缩加载。首先,样品在一定的时间间隔内受到ASR效应的影响,同时受到轴向约束。接下来,棱柱体在单轴压缩下被加载,直到被破坏为止。为了确定抗压强度退化的趋势,样本在轴向约束条件下,分别经受了0 d、122 d、243 d、365 d、488 d、610 d和730 d的ASR效应。为了研究碱含量的影响,所有试验都是在ca 为2.89 kg·m−3和3.15 kg·m−3 的条件下进行的。图18(a)和(b)对从小尺度LDPM全模拟获得的混凝土棱柱体抗压强度的变化与三种不同RVE尺寸的均质化分析结果进行了比较。由此可知,不同RVE尺寸的均质化分析结果与从小尺度LDPM分析获得的结果非常吻合。此外,由图18可知,碱含量越高,棱柱体抗压强度降低越明显,此结果已被均质化框架成功捕捉并且与LDPM的分析结果一致。此外,如先前研究结果所观察到的,对于较大的RVE尺寸,粒子划分的效果会降低,这主要表现为曲线上散射的减小。
《图18》
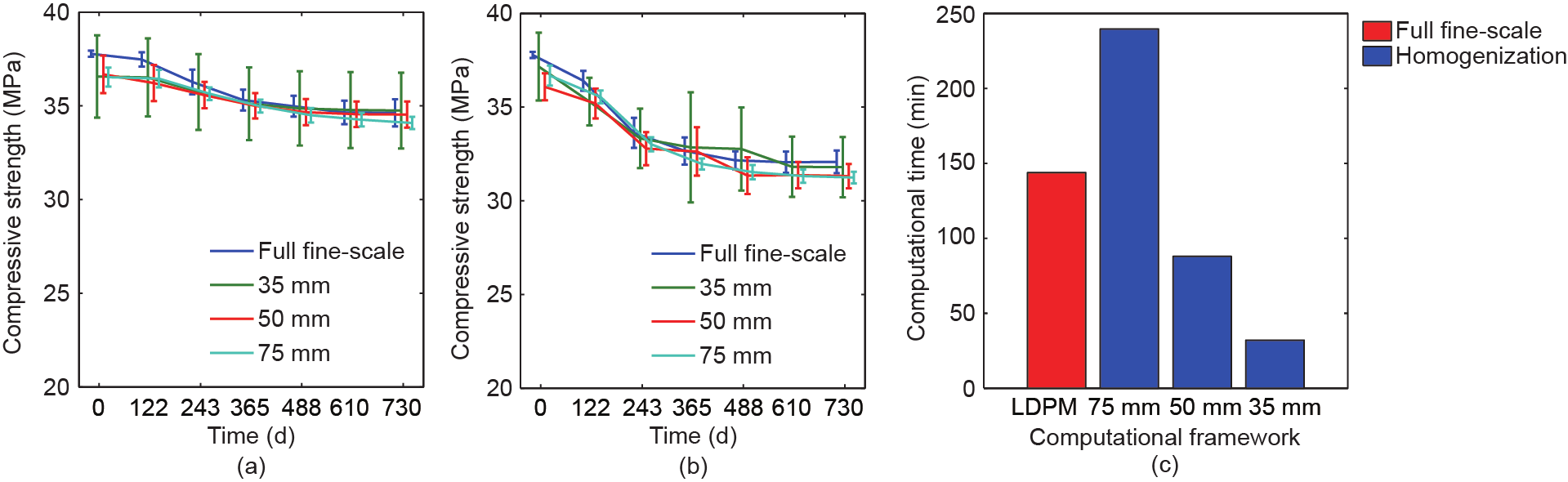
图18. 针对ca = 2.89 kg·m−3 (a)和ca = 3.15 kg·m−3 (b),对由完整小尺度LDPM分析和均质化框架获得的抗压强度进行比较; (c)比较不同RVE尺寸的完整小尺度LDPM分析和均质化分析的计算成本。
计算成本研究是多尺度方法研究的一个重要方面,没有多尺度方法,多尺度模型的开发就没有意义。在相关文献方面,对已开发的多尺度模型的计算成本效率的研究还没有对其数值精度研究得多。目前已开发的均质化框架的
显著优点是在节省计算成本的同时保证了数值结果的精度。图18(c)比较了针对不同RVE尺寸的完整小尺度LDPM分析的计算成本和均质化方法的计算成本。由此可知,使用75 mm的RVE对混凝土棱柱体进行均质化分析的计算时间比使用完整小尺度LDPM分析的计算时间大约长30%。这是因为在75 mm的RVE的均质化分析中,计算节点和LDPM四面体元素的总数要大于在完整小尺度LDPM分析中的总数。在这种情况下,RVE的体积等于宏观有限元的大小,而RVE曲面节点在有限元内表面是重复的。另外,对于50 mm和35 mm的RVE多尺度分析,其计算时间分别为完整小尺度LDPM分析的计算时间的67%和23%。应该注意的是,均质化分析仅使用了三种宏观有限元。因此,在分析由大量有限元离散化的较大结构时,节省的计算成本将更为可观。计算成本的节省是开发多尺度框架的主要目的之一,也是利用所开发的均质化方案能成功实现的。
最后,在自由膨胀和单轴压缩下,从完整小尺度LDPM分析和均质化分析获得的棱柱体的破坏模式如图19所示。由于在自由膨胀和单轴压缩条件下的应变场是均匀的,因此图19仅显示了这两种情况下每种尺寸的一种RVE的损伤轮廓。图19(a)显示了在ca = 3.9 kg·m−3 的情况下,ASR自由膨胀(无轴向约束)730 d后的试样开裂轮廓。可以看出,损伤随机分布在整个试样中,并且均质化分析也捕捉到了相似的损伤模式。图19(b)显示了在ASR膨胀243 d后,承受单轴压缩的混凝土棱柱的开裂轮廓。可以看到,小尺度分析和均质化分析都捕捉到了由于单轴变形所产生的试样横向膨胀而引起的垂直裂痕。
《图19》

图19. 当ca = 3.9 kg·m−3 时,在由ASR效应引起的自由膨胀(a)和ASR自由膨胀后的单轴压缩(b)条件下,混凝土棱柱体和不同RVE尺寸的开裂轮廓。
《4.3. 四点弯曲试验(4pbt)》
4.3. 四点弯曲试验(4pbt)
如图20(a)所示,在此数值示例中,利用完整LDPM分析法和两尺度均质化方法模拟了跨度为2.5 m,高度为0.5 m的混凝土梁。为了进行均质化分析,我们利用边长为50 mm且具有单个高斯点的六面体有限元对混凝土试样进行离散化,并将35 mm的LDPM RVE分配给每个宏观积分点。LDPM RVE和全混凝土梁LDPM样本均使用由第4节所介绍的参数生成。我们针对三种不同的ASR作用时间,即无ASR、ASR自由膨胀100 d和ASR自由膨胀150 d,对混凝土梁进行了四点弯曲试验(4pbt)。完整小尺度和均质化分析使用的ASR-LDPM参数与第4节所介绍的参数相同。所有模拟过程中的碱含量均为2.89 kg·m−3 。图20(b)对从完整的LDPM分析和均质化分析获得的力-位移(F-u)曲线进行了比较。由图可知,在压缩力峰值、弹性分支F-u 曲线下面积方面,对于无ASR效应的混凝土梁,其F-u 曲线与完整的LDPM和两尺度均质化分析结果吻合良好。峰后斜率存在差异,这是由于均质化分析中RVE尺寸小于宏观有限元尺寸。Gitman等[64]研究表明,软化响应的峰后分支由RVE尺寸控制,并且如果RVE尺寸等于有限元尺寸,则说明了该分支所消耗的能量是正确的。
《图20》
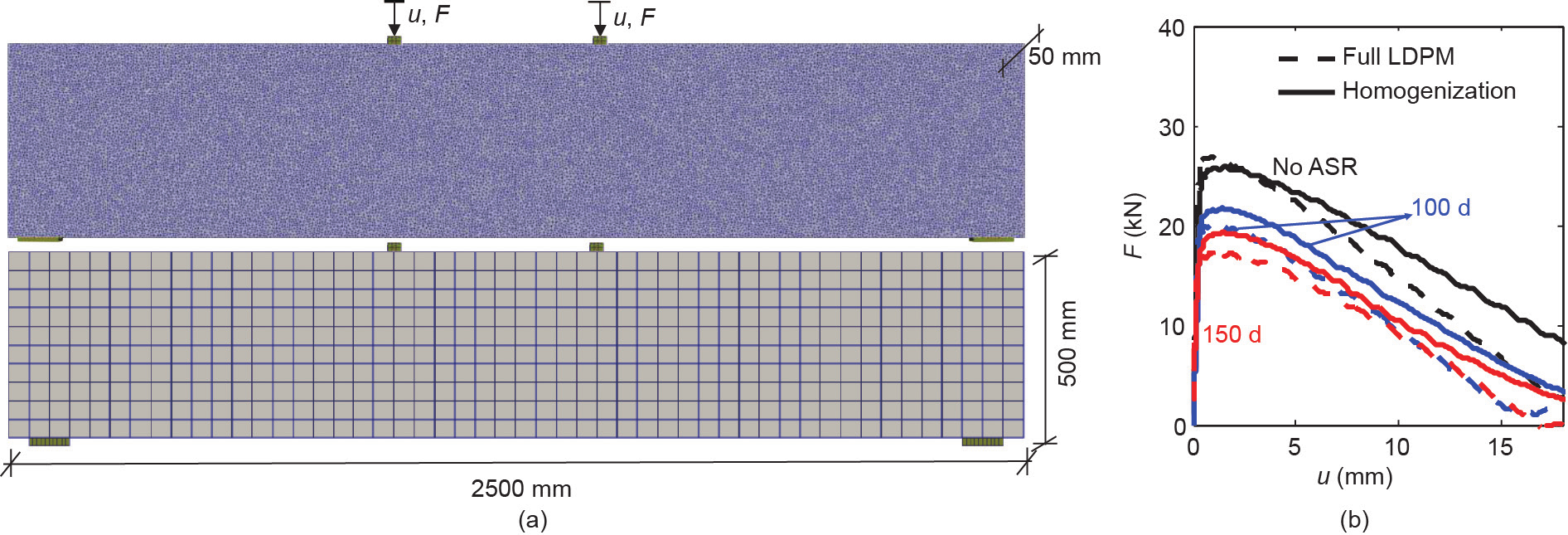
图20. (a)利用完整的LDPM和有限元对混凝土梁进行建模,用于均质化分析; (b)在无ASR、ASR自由膨胀100 d和150 d后,从完整的LDPM和均质化分析获得的F-u 曲线。
图20(b)还显示了从ASR自由膨胀100 d和150 d后的4pbt中获得的F-u 曲线。由此可知,对于ASR自由膨胀100 d和150 d,由完整的LDPM分析计算出的ASR所引起的峰值力降比从均质化分析中获得的峰值力降要高。破坏过程中裂纹在样本中的扩展路径是影响力学响应的一个重要因素。图21(a)~(c)为不同ASR阶段,在混凝土梁上进行4pbt后,LDPM样本的裂纹扩展轮廓。由图21(b)、(c)可知,在预加载的ASR自由膨胀阶段所产生的分散式微裂纹遍布了整个梁体。图21(d)显示的是,在混凝土梁被破坏时,由均质化分析所获得的在混凝土梁长度方向上的应变张量分量的轮廓。在所有三种情况下(无ASR、ASR自由膨胀100 d和ASR 150 d),该轮廓看起来都很相似。从该图可以清楚地看到,在完全LDPM分析中,由于试样的精细空间离散化,宏观裂纹遵循了使势能最小化的路径。但是,在均质化分析中,宏观裂纹在宏观有限元离散化之后被迫沿垂直方向直线生长。这种差异对于力学加载前具有ASR自由膨胀的样本更为重要,因为样本中存在分布的微裂纹。因此,均质化通过宏观有限元离散化限制了宏观裂纹的扩展路径,这可能是造成ASR自由膨胀100 d和ASR自由膨胀150 d情况下,完整LDPM和多尺度F-u 曲线之间差异的原因,如图20(b)所示。在计算成本方面,三种情况下均质化分析的模拟时间大约占整个LDPM分析运行时间的40%,这说明多尺度分析可显著提高计算效率。
《图21》
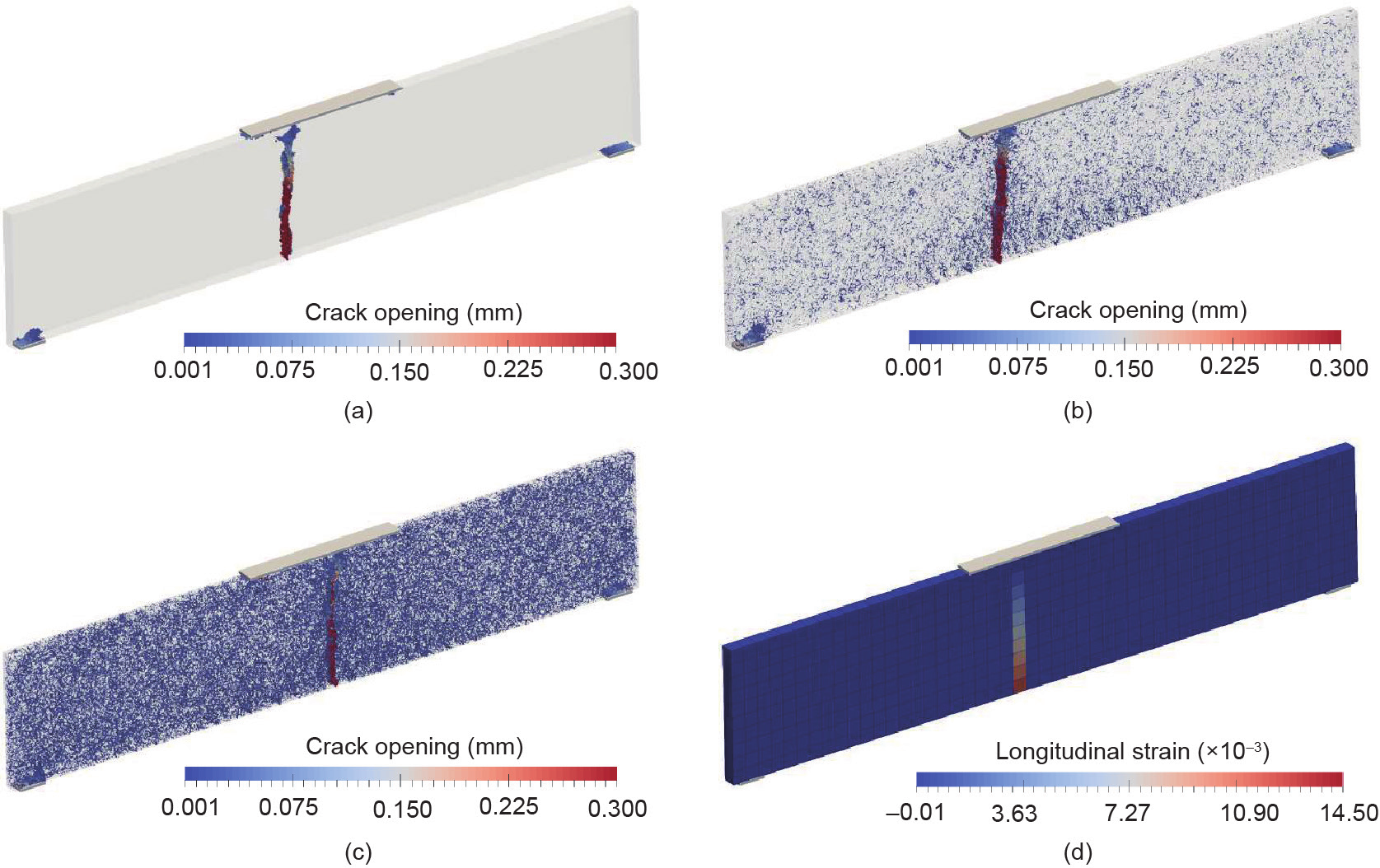
图21. 在无ASR(a)、ASR自由膨胀100 d(b)及ASR自由膨胀150 d(c)后,混凝土梁经4pbt后的开裂轮廓; (d)均质化模拟的纵向应变轮廓。
《5. 结论》
5. 结论
本文介绍了混凝土ASR多尺度均匀质化分析的理论和数值实现。在均质化框架中,中尺度粒子模型与连续体有限元模型相联系,该模型在混凝土ASR效应的建模中取得了显著效果。混凝土在力学载荷作用下的损伤和裂纹以及ASR损伤,都是在小尺度RVE中进行模拟的,而在宏观尺度上没有考虑预定的非线性行为。首先,研究表明,不同尺寸的RVE能够再现混凝土在拉伸和压缩时的力学性能退化。因此,我们选择比相应的有限元尺寸更小的RVE尺寸,从而大大节省了计算成本。接下来,我们利用多尺度均质化框架分析了由ASR引起的混凝土棱柱体的自由膨胀。
结果表明,该多尺度框架能较准确地再现由试验和完整小尺度LDPM分析得到的膨胀曲线。此外,我们还对混凝土棱柱体的抗压强度在经过几个ASR效应时间段后的退化情况进行了评估,结果表明,多尺度均质化分析结果和小尺度LDPM分析结果吻合良好。这种多尺度均质化分析的优势在于它大大降低了计算成本。研究结果表明,通过减小RVE尺寸,棱柱体均质化分析的计算时间相比小尺度LDPM分析的计算时间大大缩短,而结果的数值精度也得到了很大的保证。最后,通过大型混凝土梁的4pbt模拟,我们验证了多尺度框架与完整小尺度LDPM分析的数值精度和计算效率。
《Acknowledgments》
Acknowledgments
This material is based upon work supported by the Nuclear Regulatory Commission (NRC-HQ-60-14-G-0003).
《Compliance with ethics guidelines》
Compliance with ethics guidelines
Roozbeh Rezakhani, Mohammed Alnaggar, and Gianluca Cusatis declare that they have no conflict of interest or financial conflicts to disclose.













 京公网安备 11010502051620号
京公网安备 11010502051620号




