《1. 引言》
1. 引言
当前,制造业的数字化正处于新的工业革命的最前沿,过程工业正朝着智能制造时代(通常称为工业4.0[1])过渡。工业4.0旨在创建智能工厂,其中,①物理设备具有对应的虚拟设备,这些虚拟设备集成了智能算法,能够模拟实际过程;②此类设备在现实世界和虚拟世界中互连,并连接到集中式数据库;③在有限的人工干预下,互连的设备将基于集成的实时信息进行决策并自动处理,从而推动生产过程朝着最佳目标值发展[2]。为了实现上述工业4.0,所有工程领域已经开发了新型连续操作的机器人,以确保将可靠的科学信息从最初的可行性研究更快地传递到试验工厂[1]。化学工程中的一个应用是使用自动连续流动微反应器系统,从实时实验数据中理解并建模化学过程的动力学现象。在化学转化过程的研究中,使用在线分析和反馈控制回路来进行最优实验设计的自动化微反应器系统已成功用于:①过程性能标准的在线优化,如化学反应的百分率(称为“自我优化”)[3–7];②相互竞争的动力学模型之间的区别[8,9];③动力学模型参数的精确估算[7,10,11]。
当目标是在线识别动力学模型时(即在实验执行期间),自动化微反应器系统在反馈回路中采用基于顺序模型的实验设计(model-based design-of-experiment, MBDoE)方法来设计新实验。在顺序MBDoE中[12],历史实验的数据用于获得有关系统的信息(费希尔信息),这与候选模型结构的参数估计的不确定性有关。然后,将过去的信息用于设计未来的实验,以最大化预期信息或最小化连续参数估计中的不确定性。重复进行最小化参数不确定性的过程,直到达到参数估计值的理想精度为止。在大多数关于模型识别的研究中[10,11],基于对预期费希尔信息矩阵(Fisher information matrix, FIM)的某种度量,最优实验设计问题被表述为单目标优化问题。在稳态过程中,每个实验获得的最大信息量受到实验时间和成本的限制。在这种情况下,应该通过多目标最优实验设计方法来分析每个实验获得的信息和相关的经济和运营绩效。这将有助于以总体最优的方式设计用于模型识别的实验,并且可以解答一些问题,如在一定的花费或时间下可以达到何种信息水平。
典型的多目标优化问题涉及一组非支配的折中解决方案的确定,称为帕累托(Pareto)最优解。相应的目标向量集称为帕累托前沿[13]。解决多目标优化问题的方法通常可以分为经典方法和进化方法。在经典方法中,通过将多目标问题分解为多个单目标优化问题来求解,获得接近帕累托最优的解集,在该解法中,所有目标都集成在一起(加权求和法[14]),或除了一个目标,其他目标都受到约束(ε 约束法[15])。另一方面,进化方法产生的解决方案集在优化算法的每一次运行中都接近帕累托最优[16]。算法的选择与特定问题相关,并且需要在收敛性和计算时间之间取舍。有关各种算法及其选择的更详细说明,感兴趣的读者可以参考文献[13,17]。
在以往的动力学模型辨识中,我们采用多目标最优实验设计方法来研究基于FIM的不同标准之间的权衡,来改善生物过程系统中的参数估计问题[18]。多目标优化在模型识别的最佳实验设计中的其他应用包括基于联合模型的实验设计方法[19],该实验设计方法可同时改善参数估计和模型辨别力,以及用于提高参数精度和最小化参数相关性的实验设计方法[20]。对于高度非线性的系统,已采用多目标最优实验设计方法来最大化基于FIM的度量和最小化模型曲率,以改进基于FIM的模型识别过程[21]。此外,还讨论了在过程仿真软件界面中,如何实现具有高效决策步骤的多目标优化[22]。该方法通过分析权衡解决方案,并借助灵活的决策支持机制,实现了对具有冲突目标的流程的有效设计。参考文献 [23]讨论了多目标优化在模型开发的最优实验设计中的优势。这些学者在冲突目标帕累托边界最理想的区域中应用了统计实验设计(design-of-experiment, DoE)方法,来设计最优实验。最近,基于机器学习的多目标最优实验设计方法被应用于自动优化的流式反应器系统[4]。该方法采用贝叶斯(Bayesian)优化算法来训练和完善了近似目标响应面的高斯(Gaussian)过程代理模型。在最近的另一项研究中[24],采用了一种多目标的最佳实验设计方法,来比较使用不同实验设计标准设计碳标记实验的信息和成本。之前的工作都没有探索在在线模型识别平台中应用多目标最佳实验设计框架的可能性。这样的框架将提供一个灵活的优化平台,该平台能够在实验设计问题的每次迭代中,分析基于信息的目标函数与其他冲突目标之间的不同折中方案,并可以选择所需的折中方案,从而得到模型识别总体最佳方案。
本文提出了一个多目标最优实验设计框架,用于提高在线模型识别平台的效率。在该框架中,使用ε 约束方法[15]将最优实验设计问题转化为多目标MBDoE(multi-objective MBDoE, MBDoE-MO)优化问题,其中一个目标函数(过程经济学)被优化,另一个目标函数(基于信息的目标函数)被不同值约束。在模拟案例研究中,用该框架设计最优实验,用于识别稳态下自动流反应器中的动力学模型。该案例研究源自用于识别稳态下运行的微反应器中苯甲酸(benzoic acid, BA)和乙醇酯化的动力学模型的真实系统[25]。尽管案例很简单,但是在稳定状态下运行的流动系统中进行实验会涉及不必要的材料消耗[26−29],而且在信息量最大的情况下,材料消耗量通常达到最大,因此整个过程并不经济。所提出的多目标最优实验设计框架,通过使用基于信息的目标函数和考虑材料消耗的基于成本的目标函数,可以克服这一限制。
《2. 材料和方法》
2. 材料和方法
《2.1. 系统模型》
2.1. 系统模型
所涉及系统的可识别模型(即可以从足够的实验数据中唯一估计其参数的模型)[30]由式(1)中一般形式的一组微分和代数方程(differential and algebraic equation, DAE)表示。
式中,f 和h分别是组成动力学模型的Nf × 1和Ny × 1组公式;x是状态变量的Nx × 1数组, 是时间和空间中状态变量的一组导数[即对
是时间和空间中状态变量的一组导数[即对 来说,
来说,
 ,对
,对 来说,
来说,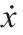
 ;u是Nu × 1受控输入数组;θ是Nθ × 1模型参数数组;t 是时间;z 是轴向域;
;u是Nu × 1受控输入数组;θ是Nθ × 1模型参数数组;t 是时间;z 是轴向域; 变量模型预测数组。
变量模型预测数组。
在线模型识别任务的目的是获得式(1)最合适的形式,并使用自动化设备生成的实时数据来估计其参数集θ的唯一值。一旦从数据中识别出合适的模型结构,就将模型识别任务简化为尽可能精确的估计模型参数θ。这是通过依次解决参数估计问题和最佳实验设计问题来实现的,直到通过统计假设检验确认了唯一的参数估计为止。实验设计问题被看作优化问题,目标是寻找最优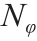 维实验设计向量
维实验设计向量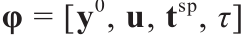 ,该向量通常包含被测变量初始条件
,该向量通常包含被测变量初始条件 维集合、受控输入u的Nu 维集合、输出变量的采样次数
维集合、受控输入u的Nu 维集合、输出变量的采样次数 维集合以及可能的实验持续时间τ 。
维集合以及可能的实验持续时间τ 。
《2.2. 所提出的框架》
2.2. 所提出的框架
针对在线模型辨识平台的实验设计问题,提出了一种多目标优化实验设计框架,以确定实验设计向量集,从而以最小的实验成本提高参数估计。框架的算法如图1所示。
《图1》

图1. 自动化模型识别平台中在线多目标最优实验设计框架,该框架用于以最小的实验成本提高在线参数估计精度。
如图1所示,自动化设备首先执行使用统计DoE方法设计的初步实验[31]。初步实验的实际数据存储在数字数据库中。从实际数据的数字记录中,使用预定义的目标函数评估过程性能。这里提出的在线模型识别框架基于两个目标:①最小化成本;②最大化期望信息。通过计算实验成本和模型参数的置信区间,可以在实验设计的每个步骤中评估过程性能。图1的模块1 (性能矩阵)对此步骤进行了说明。未来的实验旨在确定与这两个目标相对应的折中解决方案的条件。通过将实验设计问题看作最小化成本和最大化信息的多目标优化问题来得到折中条件,如图1中的模块2所示。在下一步(图1中的模块3)中,从生成的折中解决方案中选择适合下一个实验的条件,并自动执行。整个操作都是在线执行的,并迭代直到满足终止条件为止。终止标准由用户确定。常见的终止标准包括:①达到实验预算;或②主要目标预先定义的阈值。在本文中,选择准则①作为终止准则。整个框架使用Python [32]实现,并通过一个函数调用作为独立模块运行。多目标最优实验设计框架构成了所实现算法的核心部分。详细信息请参见以下各节。首先讨论了使用用于改进参数估计的MBDoE方法(MBDoE methods for improving parameter estimation, MBDoE-PE)和用于最小化实验成本(MBDoE method for minimizing experimental cost, MBDoE-cost)的MBDoE方法的最佳实验设计问题,然后讨论了MBDoE-MO的定义及其解决方法。
《2.3. MBDoE-PE》
2.3. MBDoE-PE
FIM的逆矩阵通过Cramer-Rao不等式[33,34]来估计参数方差-协方差的下限,费希尔信息矩阵已被广泛用于定义最佳实验设计中的目标函数以提高参数精度 [35]。常规MBDoE-PE被公式化为以下形式的优化问题:

式中, 指的是预测参数方差-协方差矩阵
指的是预测参数方差-协方差矩阵 的某种度量,最小化
的某种度量,最小化 以获得最佳实验设计向量
以获得最佳实验设计向量 ,该向量是尺寸为
,该向量是尺寸为 的数组,对应于N 个设计实验。
的数组,对应于N 个设计实验。 的常见选择包括参数方差-协方差矩阵的迹线、特征值和行列式,它们分别构成被称为A-最优设计、E-最优设计和D-最优设计的最优设计标准[36]。在本研究中,选择参数方差-协方差矩阵的最大特征值作为参数不确定性的度量,并通过最小化该目标函数来制定用于提高参数精度的E-最优MBDoE。优化问题的约束条件是模型方程和设计变量的
的常见选择包括参数方差-协方差矩阵的迹线、特征值和行列式,它们分别构成被称为A-最优设计、E-最优设计和D-最优设计的最优设计标准[36]。在本研究中,选择参数方差-协方差矩阵的最大特征值作为参数不确定性的度量,并通过最小化该目标函数来制定用于提高参数精度的E-最优MBDoE。优化问题的约束条件是模型方程和设计变量的 维边界,允许边界在设计空间D内变化,从而定义了这些变量的运算范围。式(2)中的预测参数方差-协方差矩阵
维边界,允许边界在设计空间D内变化,从而定义了这些变量的运算范围。式(2)中的预测参数方差-协方差矩阵 根据式(3)的FIM观测值计算得出的。
根据式(3)的FIM观测值计算得出的。

式中, 表示从第i 个实验获得的FIM观测值和代表所有n 个实验的总观测信息。类似地,
表示从第i 个实验获得的FIM观测值和代表所有n 个实验的总观测信息。类似地,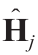 表示要设计的第j 个实验的FIM预期值,其加和表示要设计的N 个实验中的总预测信息。在模型参数的最大似然估计
表示要设计的第j 个实验的FIM预期值,其加和表示要设计的N 个实验中的总预测信息。在模型参数的最大似然估计 [34]下评估FIM观测值。使用式(4)计算第j 个设计实验的FIM预期值。
[34]下评估FIM观测值。使用式(4)计算第j 个设计实验的FIM预期值。
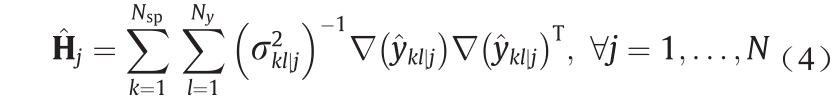
式中,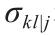 表示在第
表示在第 次实验的第k 次采样中与第
次实验的第k 次采样中与第 个响应变量测量误差的标准差;
个响应变量测量误差的标准差; 表示模型参数对第k 个采样中第
表示模型参数对第k 个采样中第 个响应变量的一阶导数的
个响应变量的一阶导数的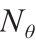 × 1维列向量,并表示对参数值响应的一阶敏感性,
× 1维列向量,并表示对参数值响应的一阶敏感性, 的转置。
的转置。
《2.4. MBDoE-cost》
2.4. MBDoE-cost
为了提高实验过程的经济性,MBDoE成本公式表示如下:

式中,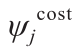 为第
为第 次实验的成本函数和表示执行N 次实验的总成本;
次实验的成本函数和表示执行N 次实验的总成本;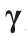 为成本函数中的一组常数参数。其优化决策变量的定义以及与模型方程和设计空间有关的约束与MBDoE-PE中的相同。
为成本函数中的一组常数参数。其优化决策变量的定义以及与模型方程和设计空间有关的约束与MBDoE-PE中的相同。
《2.5. 制定多目标最优实验设计问题》
2.5. 制定多目标最优实验设计问题
为了最小化实验成本并且提高参数估计精度,MBDoE-MO是通过ε 约束方法求解的。通过将基于FIM的目标函数限制在ε 的不同值内来最小化成本函数。MBDoE-MO优化问题的公式为:

式中,给出的MBDoE-MO优化问题的唯一解φMO 是对于任何给定的Nk 维上界向量 的帕累托最优解。使用不同的ε值可以找到不同的帕累托最优解。理想地,ε向量的选择必须使得每个ε 都位于受约束的目标函数的最小值和最大值之间。这意味着ε1 和
的帕累托最优解。使用不同的ε值可以找到不同的帕累托最优解。理想地,ε向量的选择必须使得每个ε 都位于受约束的目标函数的最小值和最大值之间。这意味着ε1 和 应该分别是受约束目标函数的最小值和最大值,也就是当前问题中参数方差-协方差矩阵ψ PE 的最大特征值。因此,ε的最小值,即ε = ε1 ,是MBDoE解决方案中用于改善参数估计的
应该分别是受约束目标函数的最小值和最大值,也就是当前问题中参数方差-协方差矩阵ψ PE 的最大特征值。因此,ε的最小值,即ε = ε1 ,是MBDoE解决方案中用于改善参数估计的 的值,即
的值,即 (φPE )而ε的最大值ε =
(φPE )而ε的最大值ε =  ,是MBDoE解决方案中用于提高过程经济学的
,是MBDoE解决方案中用于提高过程经济学的 的值,即
的值,即 (φcost )。
(φcost )。
《2.6. 帕累托最优解的选择》
2.6. 帕累托最优解的选择
当通过N个实验解决多目标优化问题设计时,通过求解式(6)获得的解向量φMO 是一个Nk × N × Nφ 的数组。为了在在线模型识别框架中导航,有必要从φMO 中选择一个解决方案作为下一个实验的条件。为此,有学者提出了一种称为权衡指数(在此称为“TO指数”)的度量算法,该算法指示帕累托曲线上任意点到与该点的最小值对应的点的距离。提出两个目标函数(如果函数互不冲突),建议分析最佳折中解φMO 的集合,并为下一个实验选择所需的折中解。使用包含在归一化目标向量ψPE′ 和ψcost′ 中的目标函数归一化值(用ψ PE′ 和ψ cost′ 表示)来评估TO指数。使用等式(7)对目标函数进行归一化。

式中,obj代表PE或成本,下面给出了用于计算每个帕累托最优解TO指数的两步算法。
《2.7. 计算 TO 指数的算法》
2.7. 计算 TO 指数的算法
(1)将两个Nk 维目标向量归一化,构造归一化目标向量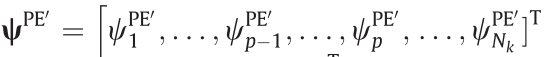 和
和 

 ,使得ψPE′ 和ψcost′ 的值落在0到1内。
,使得ψPE′ 和ψcost′ 的值落在0到1内。
(2)用以下公式评估目标空间中每个折中点的折中指数:

式中,ω1 和ω2 分别是权重因子1和权重因子2,作用于ψ PE ,用于选择折中解。
(3)选择TO指数最小的帕累托最优解作为下一组实验的条件。
上述整个解决过程如图2所示,该求解过程在每个最优参数设计的序列中,求解了多目标最优实验设计问题。
《图2》

图2. 所提出的多目标最优实验设计框架中决策步骤的图示。左图显示了从ε 约束方法获得的目标空间折中点集。从归一化折中点(如右图所示),使用权重因子ω1 和ω2 的不同值获得下一个实验的合适条件;这有助于根据用户的兴趣选择所需的折中解。
该方法是基于帕累托前沿的几何解释而开发的。如图2所示,当将帕累托目标向量归一化时,可以用坐标(0, 1)和(1, 0)表示相互冲突的目标函数的最坏折中点。帕累托曲线上任意点与最小点(0, 0)之间的距离由TO指数表示,如果函数不相互冲突,则该最小点将成为最佳点。在MBDoE-MO优化问题每次运行所涉及的决策步骤中,算法从具有最低TO指数的非支配折中点集中选择帕累托最优点。在所选帕累托点所对应的条件下进行下一个实验。当等式(8)中权重因子ω1 和ω2 被设置为1时,该算法通过同时考虑两个目标函数来选择帕累托最优解。但是,在多目标最优实验设计问题的每个序列中,也可以根据目标函数所需折中程度选择帕累托最优点。这可以通过将一个权重值在闭区间[0, 1]内调整,同时使另一个权重值保持在1。因此框架提供了可以在任何操作顺序下选择所需的折中解的灵活平台。例如,当在式(8)中ω1 = 0,ω2 = 1,该算法从成本最小化(MBDoE-cost)的角度出发,退化为单目标算法,并选择成本最小的条件作为下一个实验的条件。类似地,当将ω2 设置为0,ω1设置为1时,该算法收敛为MBDoE-PE,并选择信息量最大的条件继续进行,而无视成本。在ω1 = 0且ω2 = 1或ω1 = 1且ω2 = 0的情况下,即决策过程变为单目标,在ω1 = 0且ω2 = 1或ω1 = 1且ω2 = 0的情况下,也就是说,当决策过程成为单目标决策时,如果存在多个具有相同TO指数的折中解,算法会选择使得权重被设置为0的目标函数以达到最小的折中解。为了确保优化算法局部搜索的有效性,在框架中解决的所有最佳实验设计问题中都包含了使用拉丁超立方体采样的随机初始化步骤,与收敛有关的数值问题并未被观察到。在补充信息中讨论了初始化和上限约束对帕累托最优解的分布和收敛的影响。该算法解决每个优化问题所需的计算时间约为几秒钟。Python的科学计算库(SciPy)被用于继承模型中常微分方程系统(使用odeint工具)和解决优化问题(参数估计和实验设计)。所有的矩阵操作均使用NumPy库进行。分别使用Nelder-Mead和顺序最小二乘编程方法解决参数估计的优化问题和最佳实验设计。
《2.8. 案例研究》
2.8. 案例研究
所提出的多目标最优实验设计框架被应用于模拟案例研究,该案例与微反应器中BA和乙醇的酯化动力学模型的识别有关。以下小节中描述了该案例研究中使用的动力学模型、目标、模型假设和方法。
2.8.1. 动力学模型
BA和乙醇(ethanol, E)之间的酯化反应以苯甲酸乙酯(ethyl benzoate, EB)为主要产物,水(water, W)为副产物[37],可以表示为:
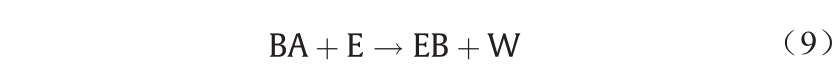
该反应被认为在稳态和等温条件下的微反应器中进行。假定由于轴向与径向尺寸之比较大,微反应器被认为是理想的活塞流反应器,径向扩散较快。假设反应器长2 m,反应过程被建模为相对于BA的一阶反应,给出了一组DAE。
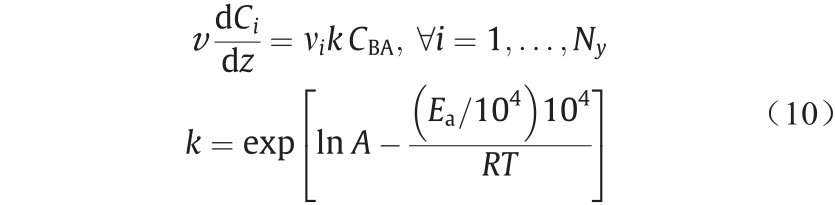
式中, 是第
是第 种物质的浓度;z 是沿着反应器长度的轴向坐标;v 是反应混合物的轴向速度;
种物质的浓度;z 是沿着反应器长度的轴向坐标;v 是反应混合物的轴向速度; 是第
是第 种物质的化学计量系数;k 是反应速率常数。式(10)给出了重新参数化的阿伦尼乌斯方程,其中,T 是反应温度;R 是摩尔气体常量。经过重新参数化,减少了参数相关性,改善了参数估计和统计检验的质量[38]。阿伦尼乌斯方程的参数即活化能
种物质的化学计量系数;k 是反应速率常数。式(10)给出了重新参数化的阿伦尼乌斯方程,其中,T 是反应温度;R 是摩尔气体常量。经过重新参数化,减少了参数相关性,改善了参数估计和统计检验的质量[38]。阿伦尼乌斯方程的参数即活化能 和指数前因子A 构成了一组需要估计的模型参数,分别以ln A 和
和指数前因子A 构成了一组需要估计的模型参数,分别以ln A 和 ×10−4 的形式被估计,即θ= [θ1 , θ2 ] T = [ln A,
×10−4 的形式被估计,即θ= [θ1 , θ2 ] T = [ln A,  ×10 −4 ]T 。
×10 −4 ]T 。
2.8.2. 目标、假设和方法
案例研究的目的是通过最小化实验成本来精确估算动力学参数。为此,将所提出的多目标实验设计框架应用于设计最佳实验集。当反应器在稳态条件下运行时,每个实验中的测量值都对应于在反应器出口采样的BA和EB的稳态浓度。因此,每个实验都涉及一个用y = 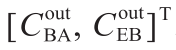 表示的测量样本。假定
表示的测量样本。假定 的测量误差为正态分布的随机变量,均值为0,标准偏差分别为0.03 mol·L−1 和0.01 mol·L−1 ;即标准偏差向量σ =[0.03 0.01]T 。
的测量误差为正态分布的随机变量,均值为0,标准偏差分别为0.03 mol·L−1 和0.01 mol·L−1 ;即标准偏差向量σ =[0.03 0.01]T 。
实验设计空间D是一个以实验设计变量的运行条件范围为边界的三维区域,这些条件是反应温度T(343~423 K),入口流速f(7.5~30 μL·min−1 )和BA的入口浓度 (0.9~1.55 mol·L−1)。实验设计问题通过求解式(2)或式(6)在空间D内为未来的实验确定最佳条件,求解哪个公式取决于使用MBDoE-PE还是MBDoE-MO。假设一个实验活动中最多允许进行7个实验,使用析因DoE方法设计了两个初步实验。这是为了确保在开始应用MBDoE之前,可以对参数进行估算,并保证信息的最小阈值。这两个初步实验的条件分别为T =413 K, f = 20 μL·min−1 ,
(0.9~1.55 mol·L−1)。实验设计问题通过求解式(2)或式(6)在空间D内为未来的实验确定最佳条件,求解哪个公式取决于使用MBDoE-PE还是MBDoE-MO。假设一个实验活动中最多允许进行7个实验,使用析因DoE方法设计了两个初步实验。这是为了确保在开始应用MBDoE之前,可以对参数进行估算,并保证信息的最小阈值。这两个初步实验的条件分别为T =413 K, f = 20 μL·min−1 ,  = 1.5 mol·L−1 和T = 393 K, f =20 μL·min−1 ,
= 1.5 mol·L−1 和T = 393 K, f =20 μL·min−1 ,  = 1.5 mol·L−1 。然后采用在线多目标最佳实验设计,自动在迭代5次的循环中依次设计接下来的5个实验。
= 1.5 mol·L−1 。然后采用在线多目标最佳实验设计,自动在迭代5次的循环中依次设计接下来的5个实验。
在实际自动运行在线模型识别系统中,如果反应混合物分析不够迅速,则采样后系统信息的获取就会出现延迟。通过重叠实验,可以在一定程度上克服这种延迟,在每次将运行实验中的样本发送到分析仪器时,便可以开始一个新的实验。为了将此概念结合到当前问题中,设计两个实验来解决第一个实验设计问题(即在实验设计问题的第一个序列中,令式(3)、式(5)和式(6)中的N = 2),这样,在对第一个设计实验的稳态浓度进行采样时,第二个实验就可以开始了。换句话说,这意味着尽管依次设计了5个实验,但仅需要解决4个最佳实验设计问题。为了进行仿真研究,使用θ* = [19.99 7.85]T 的参数值将动力学模型集成到式(10)中来生成硅内测量。此处参数集合θ* 表示模型参数的真实值。指数前因子A和活化能E a 的值分别为8.0 × 106 s−1 和7.85 ×104 J·mol−1 。
2.8.3. 成本函数的评估
在稳态条件下运行的流动反应器的动力学研究中,反应混合物被冲洗掉,直至达到稳态,并且仅将在稳态下进行的测量用于拟合模型和估计参数。因此,为了评估成本,必须确定为了达到稳态而使用的材料量,这反过来又需要估计达到稳定状态所需的时间。流动反应器系统的成本函数是通过考虑在任何实验j中冲洗掉的材料的成本来制定的,公式如下:

式中, 是实验j 达到稳态所需的时间;乘积
是实验j 达到稳态所需的时间;乘积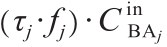 表示时间
表示时间 内冲洗掉的BA的摩尔数;
内冲洗掉的BA的摩尔数; 分别表示BA的流速和入口浓度,单位成本为1 mol BA的成本,假设为59英镑(约合74美元)。
分别表示BA的流速和入口浓度,单位成本为1 mol BA的成本,假设为59英镑(约合74美元)。
为了计算每个实验达到稳态所需的大概时间τ,使用了一种离线方法,该方法利用了之前进行的酯化反应(在与模拟系统相同的真实流动反应器系统中进行)稳态实验活动中生成的时间序列数据(即在过渡期间以固定间隔收集的数据)。之前的活动由析因实验组成,这些析因实验具有与上一节所述相同的实验设计变量和范围。所有实验均进行了1 h,以确保达到稳态。在此期间,每7 min取样一次,每次实验产生7~8个样本。该过程产生了时间序列数据。通过以下步骤,利用时间序列数据,以获得根据实验设计变量达到稳态所需时间的表达式。
步骤1:估算达到稳定状态所需的时间。在此步骤中,从时间序列数据中计算出每个实验达到稳态所需的近似时间τ 。使用基于固定窗口(本研究中的窗口大小等于3)移动平均法的算法来计算时间序列数据中测量误差的标准偏差。固定窗口大小对应于用于计算误差标准偏差的连续样本数。如果计算得出的标准误差的值小于假定的测量误差的标准差,则可以得出结论:系统已达到稳定状态,算法停止运行。对于每个实验,该算法在停留时间(等于反应器和分析回路的总体积的1.5倍除以体积流速)后生效,这是达到稳态条件的经验法则[26]。
步骤2:建立达到稳态所需时间的经验模型。在此步骤中,通过拟合步骤1中生成的数据,建立了以稳态时间为响应变量和实验条件为因素的经验模型。假定入口浓度对所需时间的影响可忽略不计。使用多项式函数来描述达到稳态所需的时间与实验条件之间的关系,如式(12)所示。
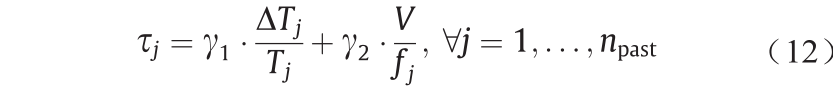
式中, 代表第j次实验达到稳态的时间;
代表第j次实验达到稳态的时间; 为温度;
为温度;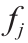 为流速;
为流速;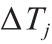 为第j次实验与第 j –1次实验之间的温差;V为反应器和分析回路(即反应器出口和HPLC取样阀之间的部分)的总体积;
为第j次实验与第 j –1次实验之间的温差;V为反应器和分析回路(即反应器出口和HPLC取样阀之间的部分)的总体积;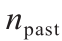 是之前实验中稳态实验的数量;
是之前实验中稳态实验的数量; 是经验模型的参数,分别与温度或流量变化后系统达到稳态所需的时间长度有关。使用最大似然估计方法,用步骤1中生成的数据来拟合多项式模型和估计参数。参数集的估计值为
是经验模型的参数,分别与温度或流量变化后系统达到稳态所需的时间长度有关。使用最大似然估计方法,用步骤1中生成的数据来拟合多项式模型和估计参数。参数集的估计值为 = [18.38, 1.83]T 。
= [18.38, 1.83]T 。
《3. 结果和讨论》
3. 结果和讨论
下面比较了两个实验设计活动。
(1)MBDoE-PE:通过最小化模型参数估计值的不确定性来改善参数估计的最佳实验设计。
(2)MBDoE-MO:多目标MBDoE用于设计最佳实验以改善参数估计,同时降低实验成本。
在第3.1节(MBDoE-PE)和第3.2节(MBDoE-MO)中报道了结果。
《3.1. MBDoE-PE—— 用于改善参数估计的 MBDoE》
3.1. MBDoE-PE—— 用于改善参数估计的 MBDoE
表1列出了设计的实验条件和在执行设计实验的每个序列中具有95%置信区间(confidence interval, CI)的参数估计的相应值。该方法涉及4个参数估计和实验设计问题的解决方案[式(2)]。如表1所示,在两次初始实验后,参数估计迅速收敛到模型参数的假定真实值θ* = [19.99 7.85]T 。这显示了所选模型与数据的紧密一致性。但是,95%置信区间是参数估计值方差的度量[34],表明参数估计值的不确定性在一开始很大。为了提高对参数估计值的置信度,在线设计了另外5个实验,目的是使参数估计中的不确定性最小。在第一个实验设计问题中,使用从初步析因实验获得的参数估计来同时设计两个实验。然后,其余三个实验在每次执行新实验并更新参数估计值时被设计出来。表1给出了所设计的实验以及置信区间为95%的参数估计值。
从结果可以明显看出,在实验过程中,参数估计的不确定性已大大降低。计算了初步实验和每个设计实验的实验成本,实验成本用于比较常规MBDoE与多目标MBDoE,以改进参数估计。实验在表1中进行了展示。
《表1 》
表1 在线MBDoE-PE的结果,包括实验设置、参数估计的后验统计以及每个设计实验的实验成本
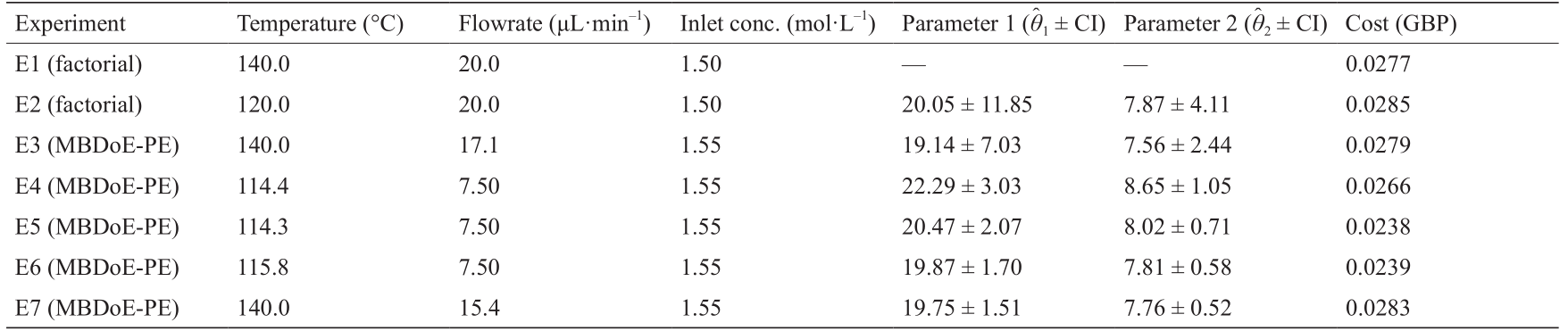
Conc.: concentration.
《3.2. MBDoE-MO—— 一种多目标 MBDoE,用于改善参数估计,同时将成本降至最低》
3.2. MBDoE-MO—— 一种多目标 MBDoE,用于改善参数估计,同时将成本降至最低
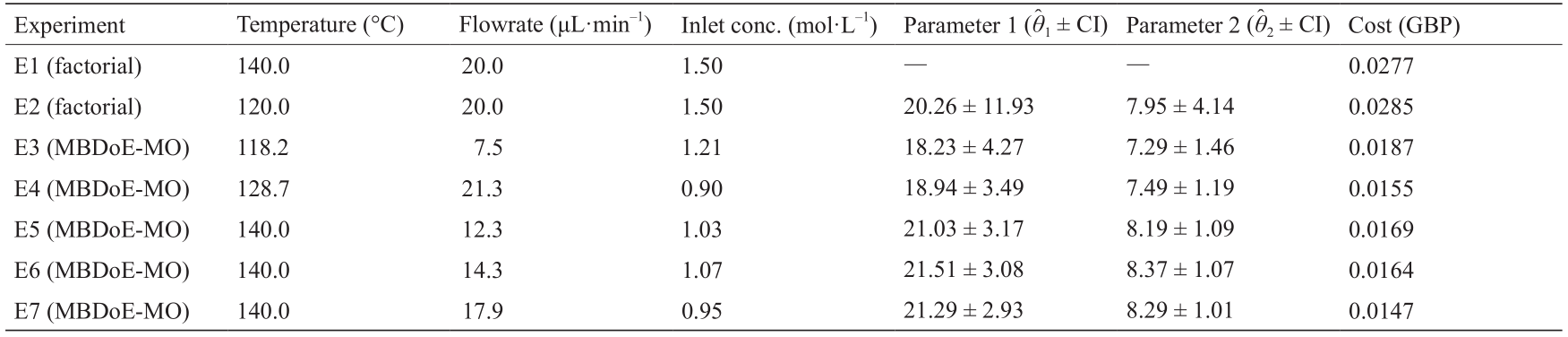
在MBDoE-MO中,以最小的实验成本改进参数估计。与MBDoE-PE相似,此方法涉及在线求解4个参数估计和最佳实验设计问题[式(6)],来设计5个最佳实验。在第一个实验设计问题中,使用从初步析因实验获得的参数更新来设计两个实验。在随后的实验设计问题中,每次从新实验更新参数估计值时,都会设计一个实验。在每个实验设计问题期间,获得了一组7个折中解,分别对应于ε 的7个不同上限值(即设置Nk = 7),决策者从中选择了帕累托最优点。每个实验设计问题中的权衡点集和选择点如图3所示。
《图3》

图3. 将MBDoE-MO用于5个实验的设计。(a)前两个实验,其中曲线的每个点对应两个最佳实验条件; (b)第三个实验; (c)第四个实验; (d)第五个实验。黑色正方形表示对应于上限变量ε 的不同值的不同折中点(非支配点/支配点)。绿色菱形表示从折中点集中选择的点,选择该点处的解作为下一组实验的条件。在所有情况下,所选点都是帕累托最优的。
如图3所示,多目标最优实验设计问题涉及与上限变量ε 的Nk 个不同值相对应的Nk 个优化问题(此处Nk = 7)的求解。在所提出的平台上在线解决了此问题。通过为权重因子ω1 和ω2 分配适当的值,可以从折中解集中选择下一个实验的适当解决方案(请参阅第2.5节)。在本问题中,将ω1 和ω2 都设置为1 [式(8)],以此选择最优折中解(两个目标同等重要)。通过为权重分配适当的值,可以根据两个目标函数之间需要的折中程度选择帕累托最优解。表2总结了多目标MBDoE的结果。如表2所示,与MBDoE-PE的结果相比,实验成本显著降低,参数估计精度略微降低。
《表2》
表2 在线MBDoE-MO的结果,包括实验的最佳设置、参数估计的后验统计以及每个设计实验的实验成本
《3.3. 结果比较》
3.3. 结果比较
比较了两个实验设计方案(MBDoE-PE和MBDoE-MO)的结果。就模型参数估计的精度而言,MBDoE-PE和MBDoE-MO均可改善连续实验设计问题中模型参数的估计。图4中参数估计值的置信区间和图5(a)中的参数统计量(95% t 值)说明了这一点。具有显著性水平α 的任何参数估计 的置信区间可以计算为:
的置信区间可以计算为:

式中,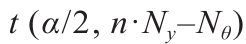 是具有
是具有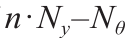 自由度和α 显著性的t 分布的双尾t 值;
自由度和α 显著性的t 分布的双尾t 值;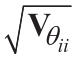 表示第
表示第 个参数估计
个参数估计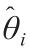 的标准偏差。任何参数估计的t 值都是参数估计与置信区间之间的比率:
的标准偏差。任何参数估计的t 值都是参数估计与置信区间之间的比率:

参考t 值是具有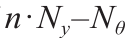 自由度和α显著性的t 分布的t 值,即
自由度和α显著性的t 分布的t 值,即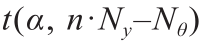 。对于任何参数估计,高于参考t 值的t 值表示该参数的统计精确估计。不出所料,与MBDoE-MO相比,MBDoE-PE可以对两个模型参数进行更精确地估计。从图4所示参数估计的置信区间的宽度可以明显看出这一点,置信区间的宽度表示估计值周围的误差范围。如图4所示,在MBDoE-PE中,两个参数均已接近真实值,最小不确定性由窄置信区间定义。参数估计值围绕真实值的微小波动可归因于模拟实验中添加的随机噪声。与MBDoE-PE相比,在MBDoE-MO中,参数估计值距离真实值相对较远,置信区间较宽。与MBDoE-MO相比,在MBDoE-PE中参数估计值的t 值更高,这也表明MBDoE-PE可以更精确地估计参数。图5(a)展示了这一点。相反,MBDoE-PE设计的信息丰富的实验比MBDoE-MO设计的实验成本高。图5(b)比较了两种方法设计的每个实验的成本。
。对于任何参数估计,高于参考t 值的t 值表示该参数的统计精确估计。不出所料,与MBDoE-MO相比,MBDoE-PE可以对两个模型参数进行更精确地估计。从图4所示参数估计的置信区间的宽度可以明显看出这一点,置信区间的宽度表示估计值周围的误差范围。如图4所示,在MBDoE-PE中,两个参数均已接近真实值,最小不确定性由窄置信区间定义。参数估计值围绕真实值的微小波动可归因于模拟实验中添加的随机噪声。与MBDoE-PE相比,在MBDoE-MO中,参数估计值距离真实值相对较远,置信区间较宽。与MBDoE-MO相比,在MBDoE-PE中参数估计值的t 值更高,这也表明MBDoE-PE可以更精确地估计参数。图5(a)展示了这一点。相反,MBDoE-PE设计的信息丰富的实验比MBDoE-MO设计的实验成本高。图5(b)比较了两种方法设计的每个实验的成本。
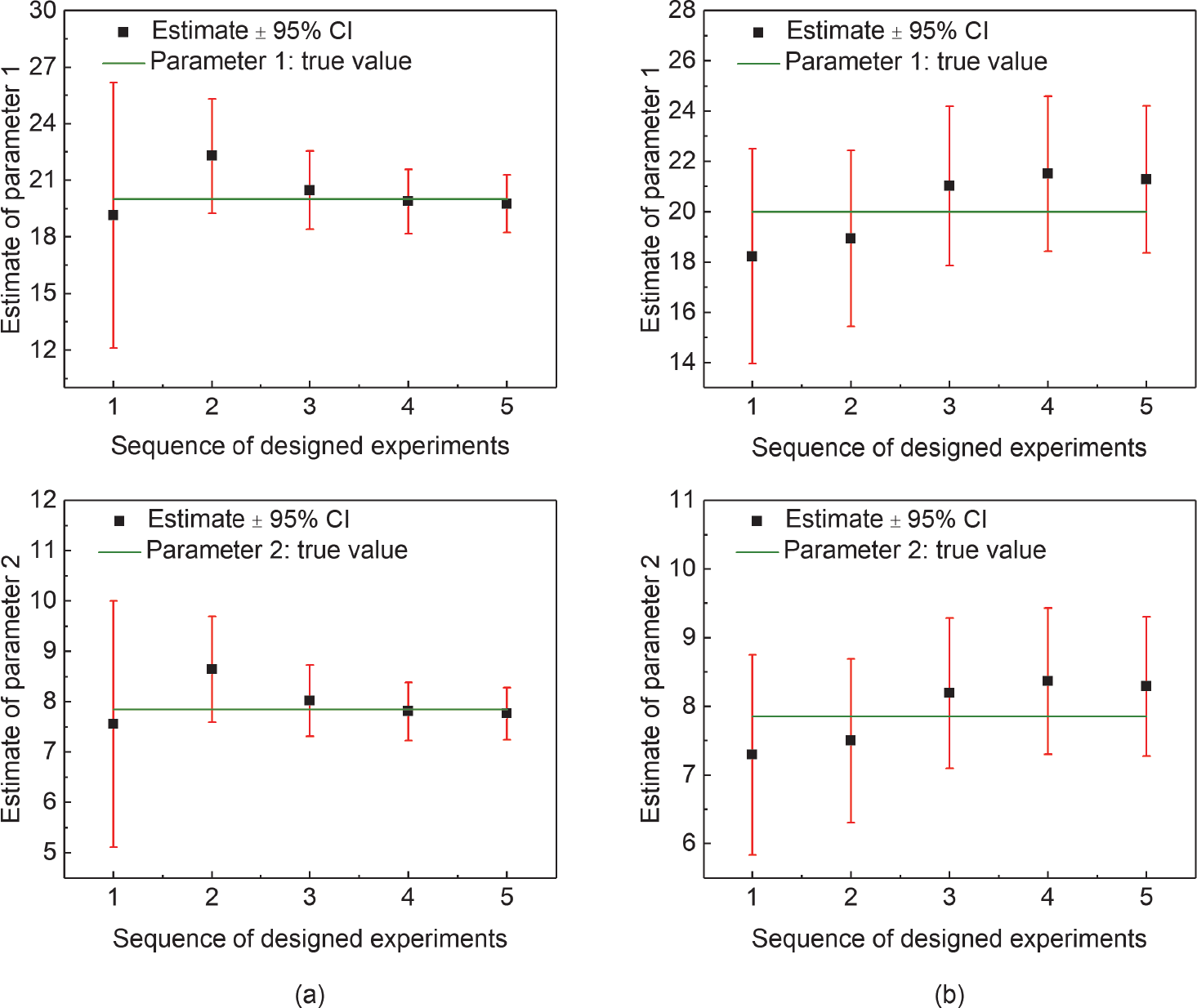
图4. 在MBDoE-PE(a)和MBDoE-MO(b)的每个实验中,模型参数的参数估计具有95%的置信区间。
《图5》
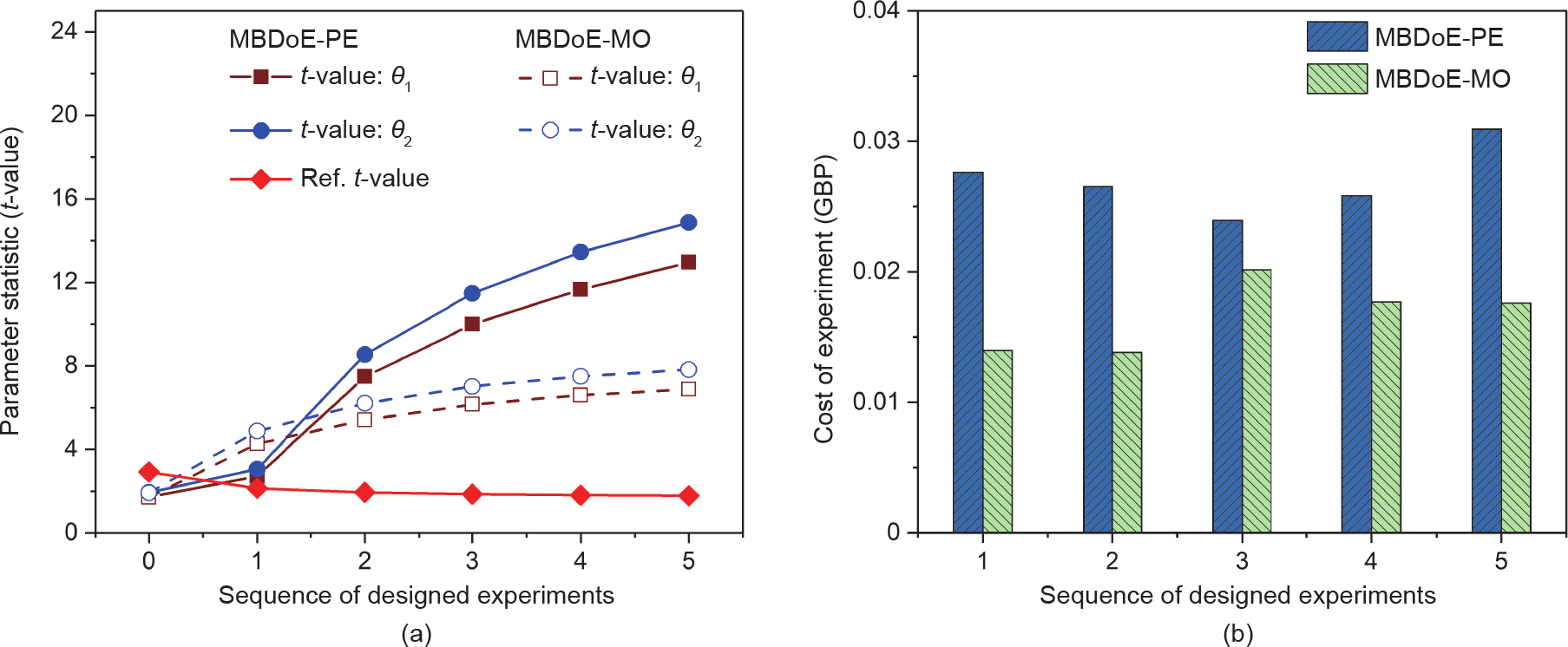
图5. 在参数统计(t 值为95%)(a)和每个实验中的材料成本(b)方面比较MBDoE-MO和MBDoE-PE的结果。在(a)中,大于参考t 值的t 值表示模型参数的精确估计。t 值越高,估计越精确。
分析图4和图5可以看出,很明显,在对成本有严格限制的情况下,多目标最优实验设计框架可以在改善参数估计和最小化成本方面提供最佳折中解决方案。图6对两种方法的实验设计变量(温度、流速和入口浓度)的分布进行了比较。在流速和反应物浓度方面,两种方法在实验条件上的差异更加明显。这是由于以下事实:所用试剂的量与入口浓度直接相关,而流速是影响达到稳态所需时间的最重要因素。反应温度和流速的分布在MBDoE-PE中遵循相似的趋势,因此高温(T ≈ 140 ℃)和低停留时间(高流速;f ≈ 17 μL·min−1 )的组合与低温(T ≈ 115 ℃)和高停留时间(低流速;f ≈ 7.5 μL·min−1 )的组合似乎有利于获得有关反应系统的信息。在MBDoE-MO中,最佳条件变为高流速和低浓度,以最大程度地减少材料消耗。
《图6》
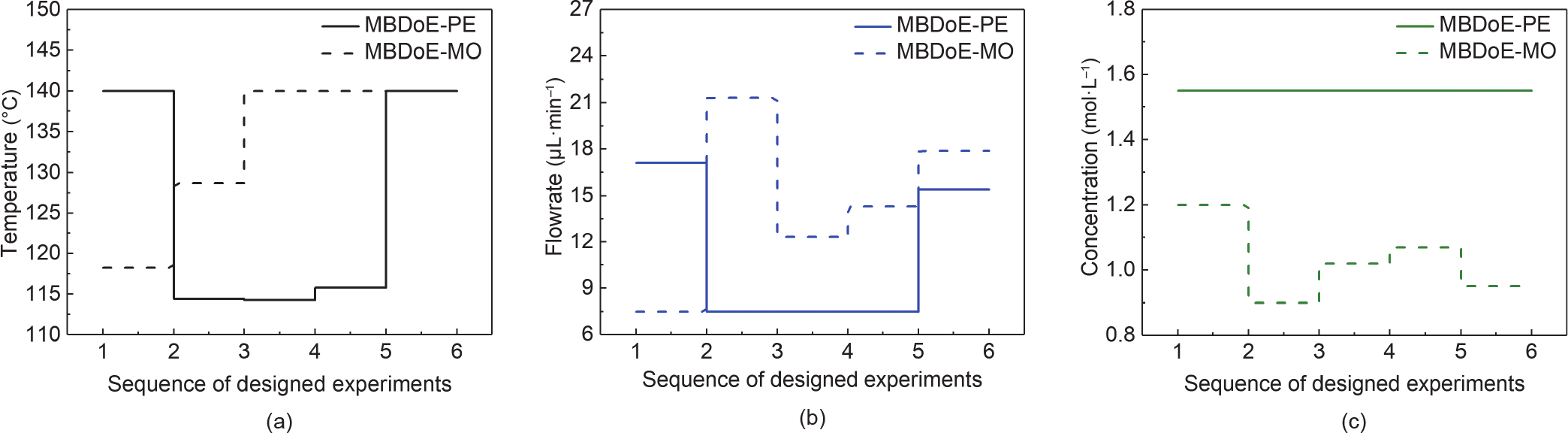
图6.比较使用MBDoE-PE和MBDoE-MO方法设计实验的最佳顺序。(a)最佳温度分布; (b)最佳流量分布; (c)MBDoE-PE(实线)和MBDoE-MO(虚线)的最佳浓度分布。
《4. 结论》
4. 结论
具有基于实时数据的反馈回路的机器人设备的出现,为化学过程的在线建模和优化提供了合适的环境。最佳实验设计可以在这种建模和优化中发挥重要作用,因为它可以根据当前数据和所需目标来计划下一步过程条件。当最佳实验设计问题涉及相互矛盾的目标时,可以选择折中得到最佳解决方案。在本文中,提出了一种用于在线多目标最佳实验设计的框架,当过程受到多个约束时,该框架可以找到用于设计实验的最佳折中解决方案。为了解决在线多目标优化问题,提出了一种由决策步骤组成的求解策略。该策略使用基于FIM的度量标准来分析折中解,从而有可能从折中解的向量中选择帕累托最优点作为下一个实验的条件。模拟案例研究中,确定了BA酯化反应的动力学模型,证明了该框架的应用价值。案例研究的结果表明,使用MBDoE-MO进行最佳实验设计是研究稳态下流动系统反应动力学的一种改进方法。这种方法可以确定最佳的折中条件,以改善从反应系统中获得的信息,同时最大程度地降低材料的消耗成本。该框架已作为Python中的常规函数被实现,并且可以扩展解决各种实际的在线多目标优化问题。
《Acknowledgements》
Acknowledgements
This work was financially supported by the PhD scholarship awarded to A. Pankajakshan from the Department of Chemical Engineering, University College London.
《Compliance with ethics guidelines》
Compliance with ethics guidelines
Arun Pankajakshan, Conor Waldron, Marco Quaglio, Asterios Gavriilidis, and Federico Galvanin declare that they have no conflicts of interest or financial conflicts to disclose.
《Nomenclature》
Nomenclature
Latin symbols
A pre-exponential factor
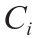 concentration of species i
concentration of species i
 concentration of species i at the reactor inlet
concentration of species i at the reactor inlet
 concentration of species i at the reactor outlet
concentration of species i at the reactor outlet
 activation energy
activation energy
 volumetric flowrate
volumetric flowrate
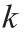 kinetic constant
kinetic constant
n number of designed experiments already performed
N number of experiments designed in one sequence of MBDoE methods
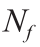 number of differential and algebraic equations constituting the model
number of differential and algebraic equations constituting the model
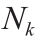 number of upper bound variable in one sequence of MBDoE-MO optimization problem
number of upper bound variable in one sequence of MBDoE-MO optimization problem
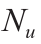 number of manipulated inputs
number of manipulated inputs
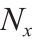 number of state variables
number of state variables
 number of measured variables
number of measured variables
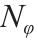 number of design variables
number of design variables
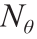 number of model parameters
number of model parameters
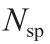 number of sampling points
number of sampling points
R ideal gas constant
t time
T temperature
v flow velocity along the axial coordinate of reactor
V volume of reactor
z axial coordinate
Matrices and vectors
D  dimensional experimental design space that bounds the admissible range of values of design variables
dimensional experimental design space that bounds the admissible range of values of design variables
f array of functions in kinetic model Nf × 1
h set of relations between the measured response variables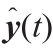 and the state variables
and the state variables 
 observed Fisher information matrix from the i-th performed experiment Nθ × Nθ
observed Fisher information matrix from the i-th performed experiment Nθ × Nθ
 predicted Fisher information matrix for the design of j-th experiment Nθ× Nθ
predicted Fisher information matrix for the design of j-th experiment Nθ× Nθ
tsp array of sampling times N sp × 1
u array of manipulated control inputs Nu × 1
 parameter variance-covariance matrix Nθ× Nθ
parameter variance-covariance matrix Nθ× Nθ
x array of state variables Nx × 1
y array of measured output variables Ny × 1
y0 array of initial conditions of measured response variables Ny × 1
 array of model predictions for the measured output variables Ny × 1
array of model predictions for the measured output variables Ny × 1
θ array of model parameters Nθ × 1
 maximum likelihood estimate of model parameters Nθ × 1
maximum likelihood estimate of model parameters Nθ × 1
θ* array of true model parameters Nθ × 1
ε upper bound vector in MBDoE-MO optimization problem Nk × 1
φ experimental design vector Nφ × 1
φcost optimal experimental design vector for MBDoE-cost problem N × Nφ
φPE optimal experimental design vector for MBDoE-PE problem N × Nφ
φMO optimal experimental design vector for MBDoE-MO optimization problem Nk × N × Nφ
ψcost′ normalized objective vector from MBDoE-cost problem Nk × 1
ψPE′ normalized objective vector from MBDoE-PE problem Nk × 1
Greek symbols
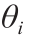
 model parameter
model parameter
 maximum likelihood estimate of the ith model parameter
maximum likelihood estimate of the ith model parameter
vi stoichiometric coefficient of the ith species
ε upper bound variable in MBDoE-MO optimization problem
τi time to reach steady state in ith experiment
 gradient operator
gradient operator
ω 1 weight factor 1, used to select trade-off solutions by acting on ψ PE
ω2 weight factor 2, used to select trade-off solutions by acting on ψ cost
 parameters of empirical model for estimating time to reach steady state
parameters of empirical model for estimating time to reach steady state
ψ PE objective function in MBDoE-PE problem
ψ cost objective function in MBDoE-cost problem
ψ PE′ normalized value of objective function in MBDoE-PE problem
ψ cost′ normalized value of objective function in MBDoE-cost problem
Acronyms
BA benzoic acid
DAE differential and algebraic equation
DoE design of experiments
EB ethyl benzoate
FIM Fisher information matrix
MBDoE model-based design of experiments
MO multi-objective
PE parameter estimation
《Appendix A. Supplementary data》
Appendix A. Supplementary data
Supplementary data to this article can be found online at https://doi.org/10.1016/j.eng.2019.10.003.














 京公网安备 11010502051620号
京公网安备 11010502051620号




