《1. 引言》
1. 引言
生成对抗网络(GAN)是无条件图像生成的主要方法之一。在对数据集进行训练后,GAN能够生成逼真的、视觉上吸引人的样本。GAN方法训练了一种无条件生成器和一种判别器,其中生成器可以将随机噪声转换成真实图像,而判别器用于测量生成样本与真实图像之间的差异。GAN已经过多次改进。其中一个突破是将最优传输(OT)理论与GAN相结合,如Wasserstein GAN(WGAN)[1]。在WGAN框架中,生成器计算了从白噪声到数据分布的OT映射,而判别器计算了真实数据分布与生成数据分布之间的Wasserstein距离。
《1.1. 流形分布假设》
1.1. 流形分布假设
GAN的成功可以通过以下事实进行解释,即GAN 有效地发现了真实数据集的内在结构。该结构可以用流形分布假设来表示,即一类特定的自然数据主要集中在一个低维流形上,且该低维流形被嵌入高维背景空间[2]。
图1显示了MNIST数据集的流形结构。每个手写数字图像的维数为28 × 28,且被看作是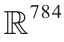 图像空间中的一个点。MNIST数据集主要集中在一个低维流形(2D 流形)附近。通过利用t-SNE流形嵌入算法[3],MNIST 数据集可被映射到一个平面区域上,而且每个图像可被映射到一个点上。表示相同数字的图像被映射到同一个集群中,这里共有10个集群,每个集群分别用不同的颜色编码。这表明MNIST数据集分布在一个二维(2D)曲面附近,该曲面被嵌入在
图像空间中的一个点。MNIST数据集主要集中在一个低维流形(2D 流形)附近。通过利用t-SNE流形嵌入算法[3],MNIST 数据集可被映射到一个平面区域上,而且每个图像可被映射到一个点上。表示相同数字的图像被映射到同一个集群中,这里共有10个集群,每个集群分别用不同的颜色编码。这表明MNIST数据集分布在一个二维(2D)曲面附近,该曲面被嵌入在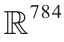 的单位超立方体中。
的单位超立方体中。
《图1》
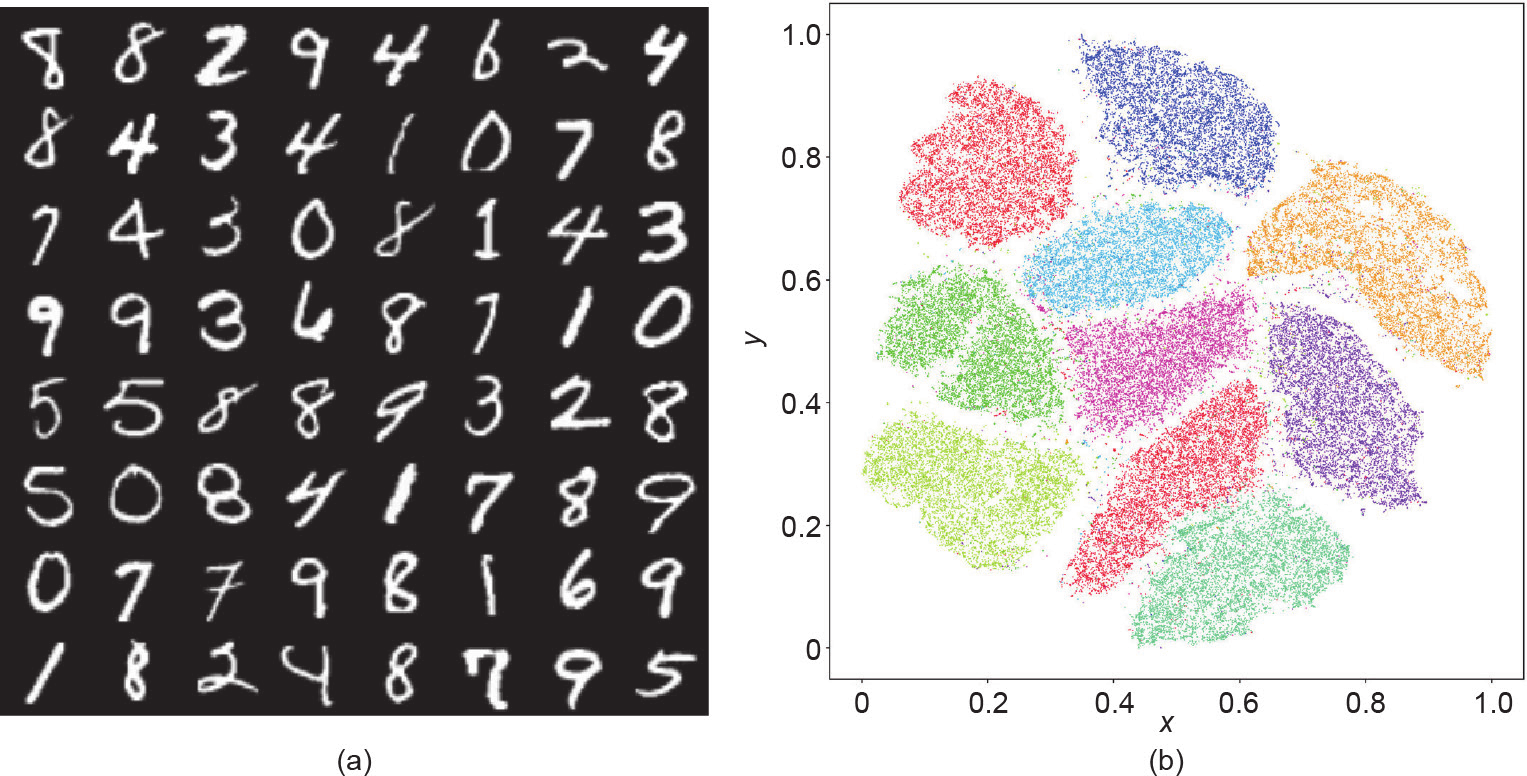
图1. MNIST数据集的流形分布。(a)MNIST数据集中的手写数字;(b)利用t-SNE算法得到的2D平面内数字的嵌入结果。将x 和y 相对坐标进行标准化。
《1.2. GAN 理论模型》
1.2. GAN 理论模型
图2显示了GAN的理论模型。真实数据分布ν 主要集中在被嵌入背景空间χ 中的流形Σ 上。(Σ, ν ) 共同揭示了真实数据集的内在结构。GAN模型计算了隐空间 Z 到流形Σ 的解码映射gθ,其中,θ\表示深度神经网络(DNN)参数。ζ 是隐空间中的Gaussian分布,gθ将ζ 前推为µθ 。判别器计算了真实数据分布ν 和生成数据分布µθ 之间的距离,如Wasserstein距离Wc (µθ , ν ),其等价于 Kontarovich势能φξ 。
《图2》

图2. GAN的理论模型。G:生成器;D:判别器。
虽然GAN有很多优点,但是它们也有一些严重的缺点。从理论上讲,我们对深度学习的基本原理的理解仍然比较粗浅。从实践来看,GAN的训练是复杂的,且其对超参数非常敏感,而且GAN经常会遇到模式崩溃问题。最近,Meschede等[4]研究了9种不同的GAN 模型及其变体,结果表明,基于梯度下降的GAN优化并不总是局部收敛的。
根据流形分布假设,自然数据集可以被表示为关于流形的概率分布。因此,GAN主要完成两项任务:①流形学习,即计算隐空间与背景空间之间的解码映射和编码映射;②概率变换,即在隐空间或图像空间中计算白噪声与数据分布之间的变换。
图3显示了生成器映射gθ = h ◦ T 的分解, 其中,h : Z →Σ 是从隐空间到背景空间中数据流形Σ 的解码映射, T : Z → Z 是概率分布变换映射。流形学习的解码映射是 h,测度变换映射是T 。
《图3》
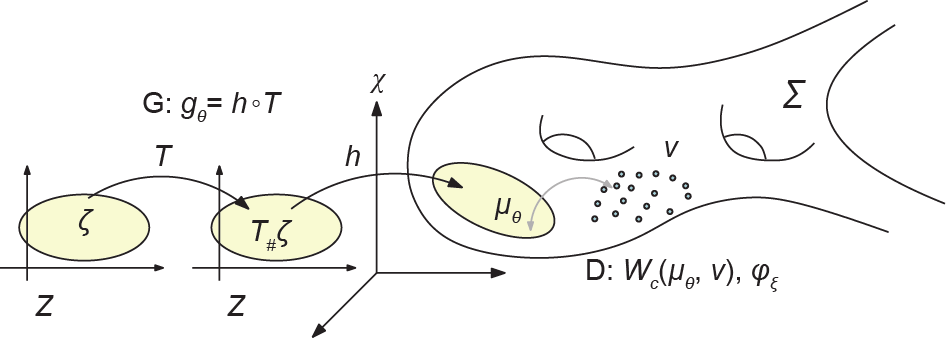
图3. 生成器映射被分解为解码映射h 和概率分布变换映射T 。T#ζ 是由 T 推导出的前推测度。
《1.3. OT 观点》
1.3. OT 观点
OT理论[5]研究的是以最经济的方式将一个概率分布转化为另一个概率分布的问题。OT理论给出了计算最优映射的严格而强大的方法,这些方法可以将一个概率分布转换为另一个概率分布,同时计算出它们之间的距离[6]。
如前所述,GAN完成了流形学习和概率分布变换两大任务。后一项任务可以通过直接使用OT方法完成。具体来说, 在图3中, 概率分布变换映射T 可以通过OT理论来计算。判别器计算了真实数据分布和生成数据分布之间的Wasserstein 距离Wc (µθ , ν ),这个可以利用OT方法直接计算得到。
从理论角度来看,GAN可以由OT理论来解释,从而使得一部分黑匣子变得透明,同时将概率分布变换过程简化为一个凸优化过程。OT理论使解的存在性和唯一性具有理论保证, 而且其收敛速度和近似程度也可以得到全面分析。
OT理论也解释了模式崩溃的根本原因。根据 Monge-Ampère方程的正则性理论,变换映射在某些奇异集上是不连续的。然而,DNN只能表达连续函数和连续映射。因此,目标变换映射位于GAN所表示的函数空间之外。这种内在的冲突使得模式崩溃问题不可避免。
OT解释还揭示了更复杂的生成器和判别器之间的关系。在现有的GAN模型中,生成器和判别器之间是相互竞争的,它们不共享中间的计算结果。OT理论表明,在L2 成本函数下,生成器和判别器的最优解可以用闭合式来相互表示。因此,生成器与判别器之间的关系应该是相互协作的而不是相互竞争的,而且它们应该共享中间的计算结果以提高计算效率。
《1.4. AE-OT 模型》
1.4. AE-OT 模型
为了降低GAN的训练难度,特别是避免模式崩溃问题,我们提出了一种基于OT理论的更简单的生成模型——自编码(AE)OT模型(AE-OT),如图4所示。
《图4》
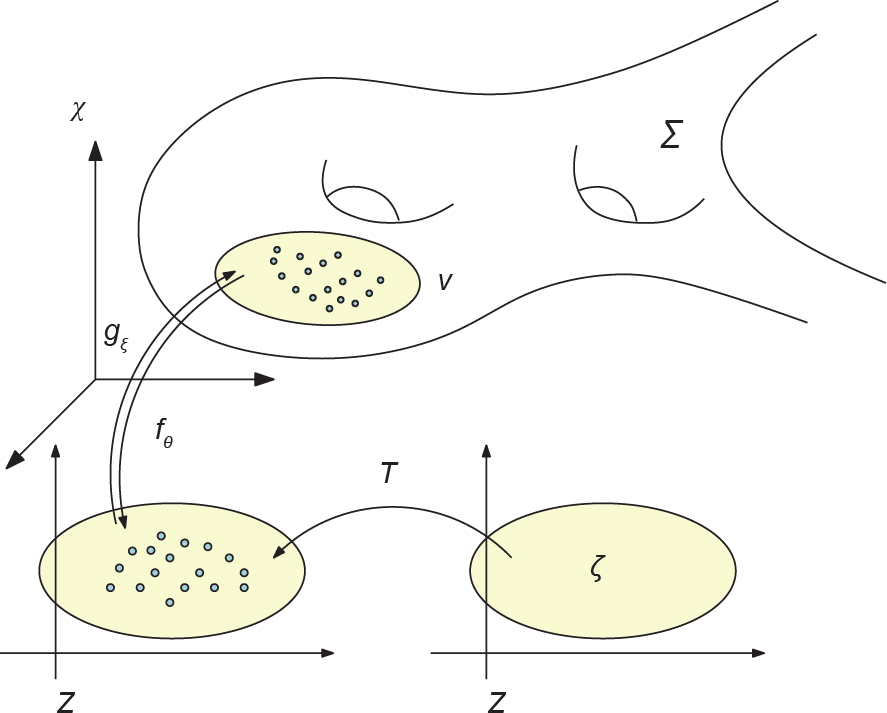
图4. 生成模型AE-OT,将AE和OT相结合。
如前所述,生成模型的两个主要任务是流形学习和概率分布变换。AE计算了编码映射fθ : Z →Σ 和解码映射gξ : Σ → Z , 目的是为了流形学习。OT映射T : Z → Z , 将白噪声ζ 变换为由编码映射(fθ)#v 前推的数据分布。
AE-OT模型有很多优点。从理论上讲,OT理论已经建立并得到了人们的充分理解。通过解耦解码映射和 OT映射,我们可以提高生成模型的理论严谨性,从而使部分黑匣子透明化。实际上,OT映射可被简化成一个凸优化问题,从而保证解的存在性和唯一性,同时使得训练过程不会仅局限于局部最优;与OT映射相关的凸能量具有明显的Hessian矩阵结构,因此,我们可以利用二阶收敛的牛顿法或超线性收敛的拟牛顿法进行优化。相比之下,现有的生成模型是以具有线性收敛性的梯度下降法为基础的。而且在AE-OT模型中,未知数的个数与训练样本的个数相等,从而避免了过度参数化的问题。在Monte Carlo方法中,采样密度可以完全控制 OT映射的误差范围。自适应等级分层算法进一步提高了计算效率。利用图形处理器(GPU)可实现并行OT 映射算法。更重要的是,AE-OT模型可以消除模式崩溃问题。
《1.5. 贡献》
1.5. 贡献
本研究运用OT理论对GAN模型进行了解释。GAN 可以完成流形学习和概率分布变换两大任务,后一项任务可以通过OT方法来实现。生成器计算了OT映射,而判别器计算了真实数据分布和生成数据分布之间的Wasserstein距离。使用Brenier定理,我们可以将生成器和判别器之间的竞争关系用协作关系来代替;根据MongeAmpère方程的正则性理论,分布变换映射的不连续性导致了模式崩溃。我们进一步提出,利用AE-OT模型来解耦流形学习和概率分布变换,从而使部分黑匣子透明化、提高训练效率以及避免模式崩溃。实验结果表明了我们所提出的方法的有效性。
本文的组织结构如下:第2部分简要回顾了OT与 GAN的相关工作;第3部分简要介绍了OT的基本理论以及Monge-Ampère方程的正则性理论;第4部分介绍了一种适合深度学习设置的用于计算OT的变分框架;第5部分从OT的角度分析了GAN模型,解释了生成器与判别器之间的协作关系(不是竞争关系),以及揭示了模式崩溃的内在原因;第6部分总结了实验结果;第7部分对全文进行了总结。
《2. 前期工作》
2. 前期工作
《2.1. 最优传输》
2.1. 最优传输
当输入域和输出域均为Dirac分布时,OT问题可被看作是一种标准线性规划(LP)任务。为了将问题扩展到大数据集,参考文献[9]的作者在原LP问题中增加了一个熵正则化器,则正则化解可以通过Sinkhorn算法被快速计算出来。后来Solomon等[10]通过引入快速卷积提高了计算效率。
第二种解决OT问题的方法是通过OT问题与凸几何之间的联系来最小化凸能量[6],从而计算出连续测度与逐点测度之间的OT映射。在参考文献[11]中,作者利用Legendre对偶理论将凸几何OT问题与Kantorovich 对偶问题联系起来。本文所提出的方法是该方法在高维空间上的一种扩展。如果输入和输出都是连续密度,求解OT问题就等价于求解著名的Monge-Ampère方程,该方程是一个高度非线性椭圆偏微分方程(PDE)。有了一个额外的虚拟时间维度,这个问题可以通过计算流体动力学来解决[12–14]。
《2.2. 生成模型》
2.2. 生成模型
在机器学习领域,能够生成复杂且高维的数据的生成模型近年来变得越来越重要。具体来说,生成模型主要被用于从给定的图像数据集中生成新的图像。在早期研究中,一些方法已被采用,如深度信念网络[15]和深度玻尔兹曼机[16]。然而,这些方法的相关训练通常比较困难和低效。后来,变分AE(VAE)方法取得了重要突破[17],其中解码器利用变分方法将Gaussian分布逼近了真实数据分布[17,18]。在此基础上,研究人员进行了一系列新的研究工作,包括对偶自编码器(AAE) [19]和Wasserstein AE(WAE)[20]。尽管VAE训练相对容易,但它们生成的图像看起来很模糊。在某种程度上,这是由于显式表达的密度函数可能无法表示真实数据分布的复杂性和无法学习高维数据分布[21,22]。后来,研究人员提出了其他非对抗性训练方法,如PixelCNN [23]、PixelRNN [24]和WaveNet [25]。然而,由于这些方法的自回归性质,新样本的生成是不能并行的。
《2.3. 对抗生成模型》
2.3. 对抗生成模型
针对上述模型的不足,研究人员提出了GAN [26]。虽然GAN是生成逼真样本的强大工具,但是它们很难被训练,而且会出现模式崩溃的问题。为了更好地训练 GAN,研究人员已经提出了各种改进措施,包括改变损失函数(如WGAN [1])以及通过剪切[1]、梯度正则化[4,27]或者光谱归一化[28]来将判别器正则化。然而, GAN的训练仍然是棘手的,需要仔细选择超参数。
《2.4. 生成模型的评估》
2.4. 生成模型的评估
生成模型的评估仍然具有挑战性。早期的工作包括概率标准[29]。然而,最近的生成模型(尤其是GAN)不适合这种评估。传统上,GAN的评估依赖于对少数示例或用户研究的可视化检查。近年来,研究人员提出了几种定量评价标准。Inception score(IS)[30]可同时测量多样性和图像质量,然而它不是距离指标。为了克服IS的缺点,研究人员在参考文献[31]中引入了Fréchet inception distance(FID)。该方法对图像的破坏具有较强的鲁棒性,而且与视觉保真度有很好的相关性。最近的研究[32]介绍了分布的精度和召回率(PRD),这两个指标用于测量真实数据分布和生成数据分布之间的精度和查全率。为了公平地评测GAN,研究人员在参考文献[33]中进行了大规模比较,在统一的网络架构下,研究人员比较了7种不同的GAN和VAE,并建立了一个通用的评价标准。
《2.5. 非对抗性方法》
2.5. 非对抗性方法
最近,研究人员也提出了各种非对抗性的方法。生成潜优化(GLO)[34]是一种“无编码器AE”的方法,其中生成模型通过非对抗性损失函数进行训练,并且取得了比VAE更好的结果。隐式最大似然估计(IMLE) [35]是一种最近点迭代(ICP)相关的生成模型训练方法。后来Hoshen和Malik [36]提出了生成式隐含最近邻(GLANN),该方法结合了GLO和GLANN的优点。该方法首先利用GLO发现了从图像空间到隐空间的嵌入,然后利用IMLE计算出了任意分布与隐藏代码之间的转换。
其他一些方法则是利用含有可控Jacobian矩阵的 DNN直接逼近了从噪声空间到图像空间的分布变换映射[37–39]。近年来,研究人员选择了一些基于能量的模型[40–42],他们利用DNN来表示能量函数,并通过 Gibb分布对图像分布进行建模。这些方法利用现有模型交替生成伪样本,然后利用生成的伪样本和真实样本对模型参数进行优化。
《3. OT 理论》
3. OT 理论
在本章中,我们将介绍经典OT理论中的基本概念和定理,重点介绍Brenier方法及其在离散集中的推广。具体细节可参考Villani的专著[5]。
《3.1. Monge 问题》
3.1. Monge 问题
假设X  是两个d 维Euclidean空间
是两个d 维Euclidean空间 的子集,µ 和υ 是被分别定义在X 和Y 上的两个概率测度,则密度函数如下:
的子集,µ 和υ 是被分别定义在X 和Y 上的两个概率测度,则密度函数如下:

假设总测度相等,即 ,那么
,那么

我们只考虑保测度的映射。Defnition 3.1(保测度映射)。如果对于任何可测集B ⊂ Y,集合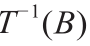 是µ- 可测的,并且
是µ- 可测的,并且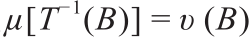 ,那么映射T : X → Y 是保测度的,即
,那么映射T : X → Y 是保测度的,即

保测度条件被记作 = υ,其中
= υ,其中 为T 诱导的前推测度。
为T 诱导的前推测度。
给定成本函数 ,该函数表示从源到目标的传输每个单位质量的代价,则定义映射T : X → Y 的总传输代价为
,该函数表示从源到目标的传输每个单位质量的代价,则定义映射T : X → Y 的总传输代价为

Monge的OT问题在于寻找使总传输成本最小的保测度映射。
Problem 3.2(Monge’s [43];MP)。给定传输成本函数 ,求使总传输成本最小的保测度映射T : X → Y ,即
,求使总传输成本最小的保测度映射T : X → Y ,即

Defnition 3.3(OT映射)。Monge的问题的解被称为OT映射。OT映射的总传输成本被称为µ 和υ 之间的Wasserstein距离,被记作Wc (µ, υ )。

《3.2. Kontarovich 的方法》
3.2. Kontarovich 的方法
根据成本函数及其测度的性质,(X, µ )和(Y, υ )之间的OT映射可能不存在。Kontarovich将传输映射扩展至传输平面,并定义了联合概率测度 ,这样ρ 的边际概率分别等于µ 和υ 。令投影映射
,这样ρ 的边际概率分别等于µ 和υ 。令投影映射 =
=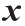 和
和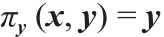 ,然后定义联合测度类如下:
,然后定义联合测度类如下:

Problem 3.4(Kontarovich;KP)。给定一个传输成本函数 ,求得联合概率测度
,求得联合概率测度 ,使得传输总成本最小。
,使得传输总成本最小。

Kontarovich的问题(KP)可以采用LP方法来求解。由于LP的对偶性,方程(7)(KP公式)可以被重新表述为对偶问题(DP),具体如下:
Problem 3.5(对偶;DP)。给定一个传输成本函数 ,求得真实函数
,求得真实函数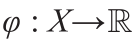 和
和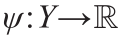 ,使得
,使得
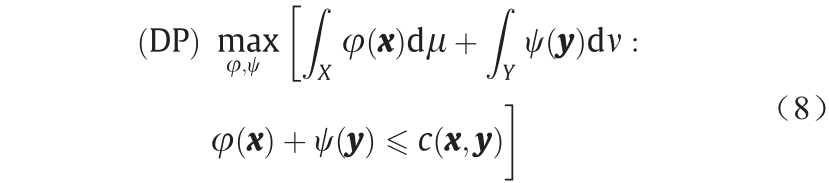
公式(8)的最大值给出了Wasserstein距离。现有的WGAN模型大多是基于L1 成本函数下的对偶形式。
Defnition 3.6(c-变换)。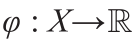 的c-变换被定义为
的c-变换被定义为 :
:
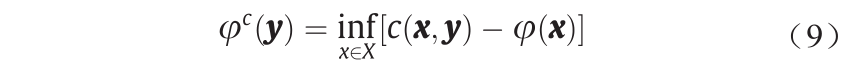
则对偶问题可被重新表述为如下形式:

《3.3. Brenier 的方法》
3.3. Brenier 的方法
对于二次Euclidean距离成本函数,Brenier [44]证明了OT映射的存在性、唯一性和内在结构。
Theorem 3.7(Brenier’s [44])。假设X 和Y 是Euclidean空间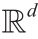 中的子集,并且传输成本是Euclidean 距离的平方,即
中的子集,并且传输成本是Euclidean 距离的平方,即 。此外,µ 是绝对连续的,而且µ 和υ 存在有限的二阶矩
。此外,µ 是绝对连续的,而且µ 和υ 存在有限的二阶矩

则存在一个凸函数 ,即所谓的Briener势能,其梯度映射
,即所谓的Briener势能,其梯度映射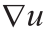 给出了Monge问题的解:
给出了Monge问题的解:
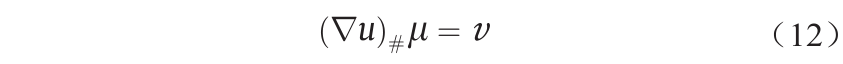
由于Brenier势能在常数范围内是唯一的,因此OT映射是唯一的。
假设Brenier势能是C 2 光滑的,则它是下面Monge-Ampère方程的解。
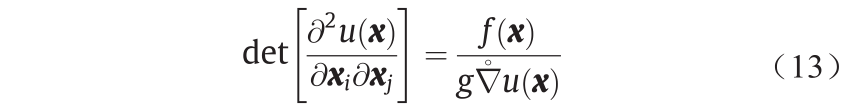
在 中,对于Euclidean空间上的L2 传输成本函数
中,对于Euclidean空间上的L2 传输成本函数 ,c-变换与经典Legendre变换之间有着特殊的关系。Defnition 3.8(Legendre变换)。给定一个函数φ :
,c-变换与经典Legendre变换之间有着特殊的关系。Defnition 3.8(Legendre变换)。给定一个函数φ : ,其Legendre变换被定义为如下形式:
,其Legendre变换被定义为如下形式:

由此可知,当 时,下面的等式成立。
时,下面的等式成立。
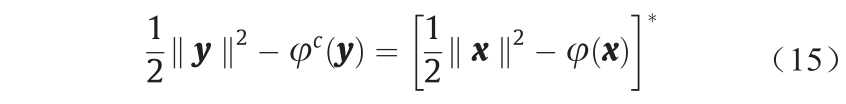
Theorem 3.9(Brenier极分解[44])。假设X 和Y 是Euclidean空间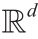 ,µ相对于Lebesgue测度是绝对连续的,且映射φ : X→Y 将µ 前推为ν ,即
,µ相对于Lebesgue测度是绝对连续的,且映射φ : X→Y 将µ 前推为ν ,即 =υ,则存在一个凸函数
=υ,则存在一个凸函数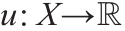 ,使得φ =
,使得φ = 。式中,s : X→X 是保测度的,即
。式中,s : X→X 是保测度的,即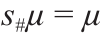 。此外,这个分解是唯一的。
。此外,这个分解是唯一的。
下面的定理在OT理论中是众所周知的。
Theorem 3.10(Villani [5])。给定凸紧区域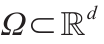 上定义的测度µ 和υ,这里存在一个成本函数为
上定义的测度µ 和υ,这里存在一个成本函数为 =
=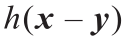 的OT平面ρ,其中h 是严格凸的。假定µ 是绝对连续的,并且∂Ω 为零测度,则ρ 是唯一的,且其具有(id, T# )µ(id:恒等映射)的形式。另外,这里存在一个Kantorovich势能φ,而且映射T 可用下式表示为:
的OT平面ρ,其中h 是严格凸的。假定µ 是绝对连续的,并且∂Ω 为零测度,则ρ 是唯一的,且其具有(id, T# )µ(id:恒等映射)的形式。另外,这里存在一个Kantorovich势能φ,而且映射T 可用下式表示为:

在这种情况下,Brenier势能u和Kantorovich势能φ 有如下关系:
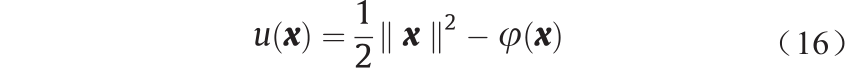
《3.4. OT 映射的正则性》
3.4. OT 映射的正则性
令Ω 和Λ 是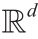 中两个有边界的光滑开集,令µ =
中两个有边界的光滑开集,令µ = 是
是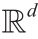 上两个概率测度,那么
上两个概率测度,那么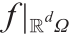 =0和
=0和 = 0。设f 和g 在Ω 和Λ 上分别是非零和非无穷的。
= 0。设f 和g 在Ω 和Λ 上分别是非零和非无穷的。
3.4.1. 凸目标域
Defnition 3.11(Hölder 连续)。一个实值函数或复值函数f 在d 维Euclidean空间中满足Hölder条件,或者它是Hölder连续时,此时存在非负实常数C,且α > 0,使得 对于f 定义域中的所有x 和y 都成立。
对于f 定义域中的所有x 和y 都成立。
Defnition 3.12(Hölder空间)。Hölder空间为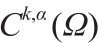 ,其中Ω 是某个Euclidean空间的一个开子集,并且整数k ≥0,它是由在Ω 上有直到k 阶连续偏导数的函数组成,从而使得k 阶偏导数是α 阶Hölder连续的,且0 < α ≤ 1。
,其中Ω 是某个Euclidean空间的一个开子集,并且整数k ≥0,它是由在Ω 上有直到k 阶连续偏导数的函数组成,从而使得k 阶偏导数是α 阶Hölder连续的,且0 < α ≤ 1。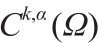 意味着上述条件适用于Ω 的任意紧子集。
意味着上述条件适用于Ω 的任意紧子集。
Theorem 3.13(Caffarelli [45])。如果Λ 是凸的,那么Brenier势能u 是严格凸的,此外,
(1)如果  ,当λ > 0时,g≤1/λ,那么u ∈
,当λ > 0时,g≤1/λ,那么u ∈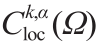 。
。
(2)如果f ∈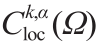 和g ∈
和g ∈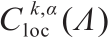 ,并且 f, g > 0,那么u ∈
,并且 f, g > 0,那么u ∈ 且[k ≥ 0,
且[k ≥ 0, 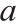 ∈ (0.1)]。
∈ (0.1)]。
3.4.2. 非凸目标域
如果Λ 是非凸的且存在光滑的f 和g,那么 ,而且OT映射
,而且OT映射 在奇异点处是非连续的。
在奇异点处是非连续的。
Defnition 3.14(次梯度)。给定开区间 和一个凸函数
和一个凸函数 ,对于
,对于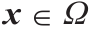 ,u 在x 点的次梯度(次微分)可被定义为如下形式:
,u 在x 点的次梯度(次微分)可被定义为如下形式:

显然, 是一个闭凸集。从几何学来看,如果p ∈
是一个闭凸集。从几何学来看,如果p ∈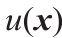 ,那么超平面
,那么超平面 在x 点从下方触碰到了u,即Ω 中的
在x 点从下方触碰到了u,即Ω 中的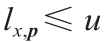 并且
并且 ,其中
,其中 是u 在x 点处的支撑平面。
是u 在x 点处的支撑平面。
如果Brenier势能u 的次梯度∂u (x )包含一个点,则u 在x 点处可微。我们根据次梯度的维数对这些点进行分类,并且定义集合 =
=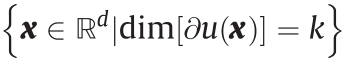 ,
,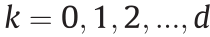 。
。
可以看出,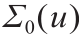 是正则点的集合,而
是正则点的集合,而 是奇异点的集合,其中k > 0。我们也定义了x 点的可达次梯度,具体如下:
是奇异点的集合,其中k > 0。我们也定义了x 点的可达次梯度,具体如下:
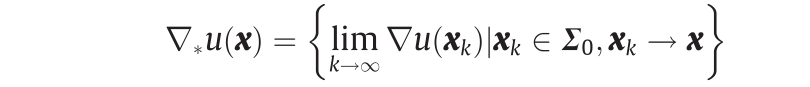
由此可知,次梯度等于可达次梯度的凸包,即

Theorem 3.15(正则性)。令Ω, Λ 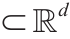 为两个有边界的开集,并且令
为两个有边界的开集,并且令 为两个概率密度函数,该密度函数在Ω 和Λ 之外为0,而在Ω 和Λ 上则界于0和无穷之间。Theorem 3.7中的OT映射被表示为T =
为两个概率密度函数,该密度函数在Ω 和Λ 之外为0,而在Ω 和Λ 上则界于0和无穷之间。Theorem 3.7中的OT映射被表示为T =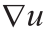 :Ω → Λ 。那么存在两个相对闭集
:Ω → Λ 。那么存在两个相对闭集 ,且
,且 =
=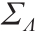 =0,当常数α >0时,使得
=0,当常数α >0时,使得 是属于
是属于 类的拓扑同胚。
类的拓扑同胚。
我们称 为OT映射
为OT映射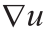 :Ω → Λ 的奇异集。图5给出了基于Theorem 4.2的算法所计算出的奇异点集结构。具体形式如下:
:Ω → Λ 的奇异集。图5给出了基于Theorem 4.2的算法所计算出的奇异点集结构。具体形式如下:

 点的次梯度
点的次梯度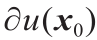 整个覆盖了Λ 内部孔洞,而
整个覆盖了Λ 内部孔洞,而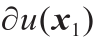 覆盖了阴影三角形区域。对于
覆盖了阴影三角形区域。对于 上的每个点,
上的每个点,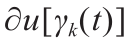 是Λ 外部的一条线段。
是Λ 外部的一条线段。 的分歧点。Brenier势能在Σ 1 和Σ 2 上是不可微的,OT映射
的分歧点。Brenier势能在Σ 1 和Σ 2 上是不可微的,OT映射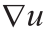 在Σ 1 和Σ 2 上是不连续的。
在Σ 1 和Σ 2 上是不连续的。
《图5》
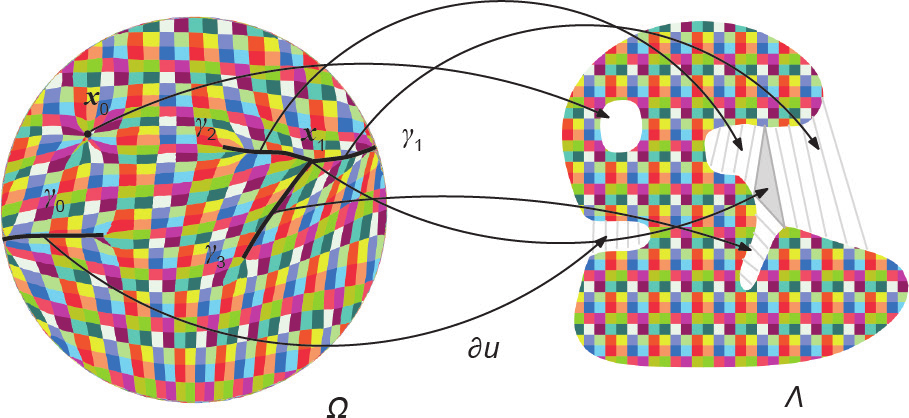
图5. OT映射的奇异点集结构。
《4. 计算方法》
4. 计算方法
Brenier定理可以被直接推广到离散情形中。在GAN模型中,源测度µ 是一个被定义在紧凸集Ω 上的均匀(或高斯)分布;目标测度ν 被表示为经验测度,它是Dirac测度的总和,即

式中,Y = 是训练样本,其权重为
是训练样本,其权重为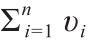 =
= ;δ 是特征函数。
;δ 是特征函数。
每个训练样本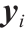 对应一个Brenier势能的支撑平面,且用下式表示,即
对应一个Brenier势能的支撑平面,且用下式表示,即
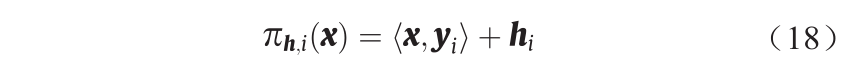
式中,支撑平面的截距(高度)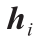 是未知变量。我们将所有的高度变量记为
是未知变量。我们将所有的高度变量记为 。
。
Euclidean空间中一族超平面的包络是一个超曲面,它与该族的每个成员都相切于某一点,这些切点共同构成了整个包络超曲面。如图6所示,Brenier势能 :
: 是一个由
是一个由 确定的分片线性凸函数,这个凸函数是它所有支撑平面的上包络,即
确定的分片线性凸函数,这个凸函数是它所有支撑平面的上包络,即

《图6》
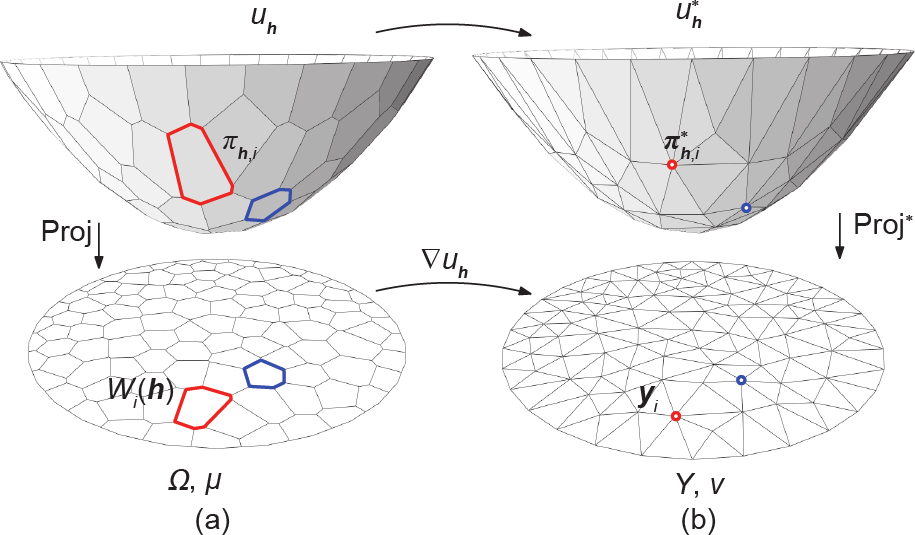
图6. 分片线性Brenier势能函数(a)及其Legendre变换 (b)。
(b)。 :
: 的Legendre对偶;
的Legendre对偶; 的梯度;Proj:投影映射;Proj*:Legendre对偶空间内的投影映射。
的梯度;Proj:投影映射;Proj*:Legendre对偶空间内的投影映射。
Brenier势能图是一个凸多面体。每一个支撑平面 对应多面体的一个面。多面体的投影诱导了Ω 的一个单元分解,其中每个支撑平面
对应多面体的一个面。多面体的投影诱导了Ω 的一个单元分解,其中每个支撑平面 的投影形成一个单元
的投影形成一个单元 ,而p 是
,而p 是 中的任意一点,具体如下:
中的任意一点,具体如下:

这个单元分解是一个功率图。 的µ 测度被记为
的µ 测度被记为 ,即
,即
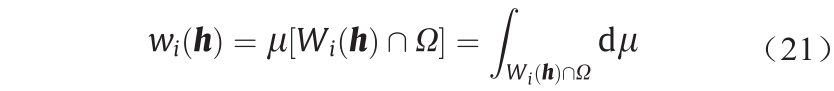
梯度映射 将每个单元
将每个单元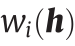 映射为一个点
映射为一个点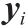 ,即
,即

如果公式(17)中目标测度υ已知,则由公式(19)可得到一个离散的Brenier势能,且该势能的每个支撑平面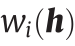 投影的µ-体积等于给定的目标测度υi 。这个结论已被Alexandrov [46]在凸几何中证明。
投影的µ-体积等于给定的目标测度υi 。这个结论已被Alexandrov [46]在凸几何中证明。
Theorem 4.1(Alexandrov [46])。假设Ω 是一个紧凸多面体,其在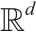 中内部非空;
中内部非空;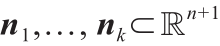 是 k 个不同的单位向量;第(n +1)个坐标是负的以及υ1 , ..., υk > 0,使得
是 k 个不同的单位向量;第(n +1)个坐标是负的以及υ1 , ..., υk > 0,使得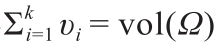 。则存在凸多面体P
。则存在凸多面体P  恰有k 个余维数为1的平面F1 ,..., Fk ,使得
恰有k 个余维数为1的平面F1 ,..., Fk ,使得 是
是 的法向量,且Ω 与
的法向量,且Ω 与 投影之间的交集体积为υi 。此外,P在垂直平移下唯一。
投影之间的交集体积为υi 。此外,P在垂直平移下唯一。
Alexandrov对解的存在的证明是以代数拓扑为基础进行的,其不具构造性。最近,Gu等[6]基于变分方法给出了构造性证明。
Theorem 4.2(参考文献[6])。令µ 是一个被定义在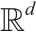 中紧凸区域Ω 上的概率测度,令
中紧凸区域Ω 上的概率测度,令 是
是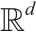 中的一组不同点。那么,对于任意υ1 , υ2 ,..., υn > 0,其中
中的一组不同点。那么,对于任意υ1 , υ2 ,..., υn > 0,其中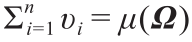 ,存在
,存在 ,在相差一个常数(c, c,..., c )的意义下唯一,使得对于所有1 ≤ i ≤ n,
,在相差一个常数(c, c,..., c )的意义下唯一,使得对于所有1 ≤ i ≤ n,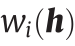 = υi 。向量h 是以下凸能量的唯一最小变元,
= υi 。向量h 是以下凸能量的唯一最小变元,
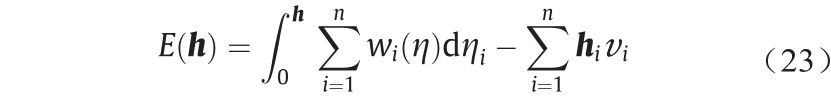
在开凸集上被定义为

此外, 在所有的传输映射
在所有的传输映射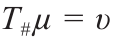 中的最小化二次成本为
中的最小化二次成本为
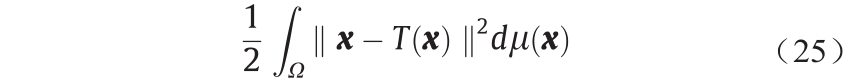
公式(23)中上述凸能量的梯度由下式给出。
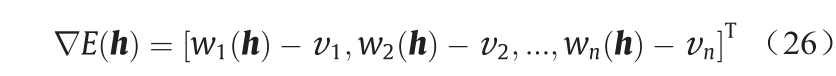
能量的第i 行和第j 列的Hessian元素可由下式给出。
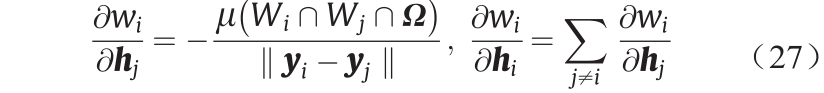
如图6所示,Hessian矩阵具有明确的几何意义。图6(a)显示了离散的Brenier势能uh ,图6(b)显示了Hessian矩阵由Definition 3.8所定义的Legendre变换 。Legendre变换可以用几何方法来构造,即对于每个支撑平面
。Legendre变换可以用几何方法来构造,即对于每个支撑平面 ,我们构造了对偶点
,我们构造了对偶点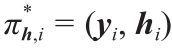 ,其中对偶点的凸包
,其中对偶点的凸包 是Legendre变换
是Legendre变换 的图。
的图。
 的投影诱导了
的投影诱导了 的加权Delaunay三角剖分。如图7所示,公式(20)中的power diagram和加权Delaunay三角剖分是彼此的Poincaré对偶,即在power diagram中,如果
的加权Delaunay三角剖分。如图7所示,公式(20)中的power diagram和加权Delaunay三角剖分是彼此的Poincaré对偶,即在power diagram中,如果 相交于某个(d−1)维单元,则在加权的Delaunay三角剖分中,
相交于某个(d−1)维单元,则在加权的Delaunay三角剖分中, 相连。公式(27)中Hessian矩阵的元素是power diagram中(d −1)维单元的µ-体积与加权Delaunay三角剖分中对偶边的长度之间的比率。
相连。公式(27)中Hessian矩阵的元素是power diagram中(d −1)维单元的µ-体积与加权Delaunay三角剖分中对偶边的长度之间的比率。
《图7》
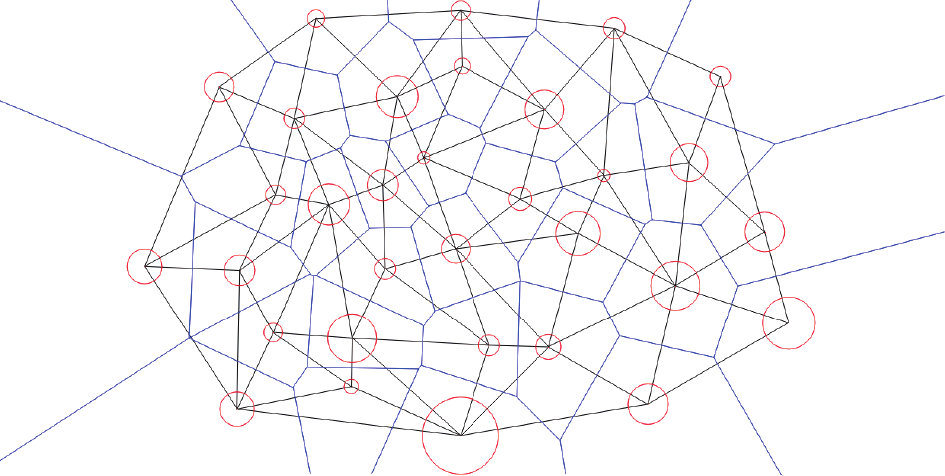
图7. Power diagram(蓝色)和其对偶加权Delaunay三角剖分(黑色)。
传统的power diagram与上述定理密切相关。
Defnition 4.3. (power 距离)。给定具有power权重 的点
的点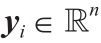 ,power距离可由下式给出。
,power距离可由下式给出。

Defnition 4.4. (power diagram)。给定加权点
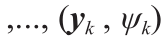 ,power diagram是
,power diagram是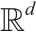 的单元分解,即
的单元分解,即
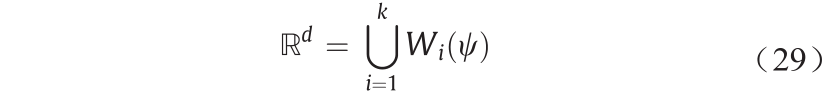
这里的每个单元都是凸多面体,即

加权Delaunay三角剖分用 表示,它是power diagram的Poincaré对偶,如果
表示,它是power diagram的Poincaré对偶,如果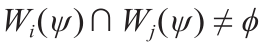 ,则在加权Delaunay三角剖分中存在连接
,则在加权Delaunay三角剖分中存在连接 的边。注意,
的边。注意, 等价于
等价于
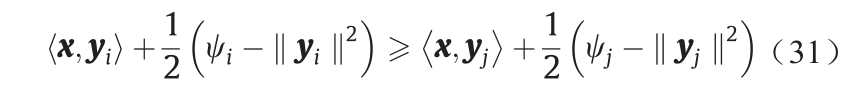
令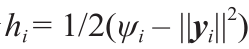 ,我们将
,我们将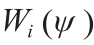 的定义重写为
的定义重写为

在实践中,我们的目标是通过优化凸能量方程(23)来计算离散Brenier势能方程(19)。对于低维情况,我们可以通过计算梯度方程(26)和Hessian矩阵方程(27)来直接使用牛顿法。对于深度学习的应用,直接计算 Hessian矩阵是不可行的,我们可以使用梯度下降法或超线性收敛的拟牛顿法。梯度下降法的关键是估计µ 体积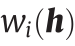 。我们可以通过使用Monte-Carlo方法来完成,即我们从分布µ 中随机抽取n 个样本,并计算落入
。我们可以通过使用Monte-Carlo方法来完成,即我们从分布µ 中随机抽取n 个样本,并计算落入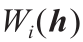 的样本数,该样本数是收敛到µ- 体积的比率。此方法是完全并行的,并可以通过GPU来实现。此外,我们可以使用等级分层方法来进一步提高效率。首先,我们将目标样本按聚类簇进行分类,然后计算目标样本到聚类簇质心的OT映射;其次,对于每个聚类簇,我们计算了从相应单元到聚类簇内原始目标样本的OT映射。
的样本数,该样本数是收敛到µ- 体积的比率。此方法是完全并行的,并可以通过GPU来实现。此外,我们可以使用等级分层方法来进一步提高效率。首先,我们将目标样本按聚类簇进行分类,然后计算目标样本到聚类簇质心的OT映射;其次,对于每个聚类簇,我们计算了从相应单元到聚类簇内原始目标样本的OT映射。
为了避免模式崩溃,我们需要找到Ω 中的奇异点集。如图8所示,目标Dirac测度有两个聚类簇,源是单位平面圆盘上的均匀分布。Brenier势能函数的图是中间带有脊线的凸多面体。脊线在圆盘上的投影是奇异点集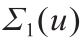 ,OT映射在Σ1上是不连续的。在一般情况下,如果两个单元
,OT映射在Σ1上是不连续的。在一般情况下,如果两个单元 相邻,那么我们可计算相应支撑平面的法线之间的角度为:
相邻,那么我们可计算相应支撑平面的法线之间的角度为:
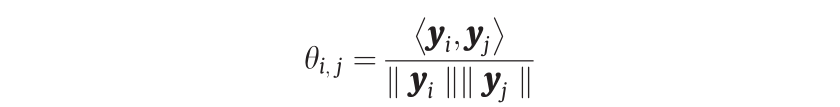
如果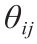 大于阈值,则公共平面
大于阈值,则公共平面 位于不连续奇点集中。
位于不连续奇点集中。
《图8》

图8. Brenier势能函数的奇异点集与OT映射的间断点集。
《5. GAN 和最优传输》
5. GAN 和最优传输
OT理论为GAN奠定了理论基础。最近的研究成果,如WGAN [1]、WGAN-GP [27]和RW-GAN [47],都使用了Wasserstein距离来度量已生成的数据分布与实际数据分布之间的偏差。
从OT角度来看,生成器与判别器最优解之间存在一个闭合式,因此生成器与判别器之间应该是相互合作的而不是竞争的。更多细节见参考文献[11]。此外, Monge-Ampère解的正则性理论可以解释GAN的模式崩溃[48]。
《5.1. 竞争与合作》
5.1. 竞争与合作
图2显示了WGAN [1]的OT视图。根据流形分布假设,真实数据分布υ 与一个被嵌入背景空间χ 中的流形Σ 非常接近。生成器计算了从隐空间Z 到背景空间的解码映射gθ,并且把白噪声ζ(如Gaussian分布)变换为生成分布µθ 。通过计算Kantorovich势能φξ,判别器计算了µθ 和真实分布υ 之间的Wasserstein距离Wc (µθ, υ )。gθ 和φξ 都是通过DNN来实现的。
在训练过程中,生成器通过优化gθ 以使 能更好地逼近υ;判别器通过优化Kantorovich势能φξ 来改善对Wassertein距离的估计,生成器和判别器相互竞争、不共享中间结果。在L1 成本函数下,WGAN的交替训练过程可以被看作是期望值的最小-最大优化过程:
能更好地逼近υ;判别器通过优化Kantorovich势能φξ 来改善对Wassertein距离的估计,生成器和判别器相互竞争、不共享中间结果。在L1 成本函数下,WGAN的交替训练过程可以被看作是期望值的最小-最大优化过程:
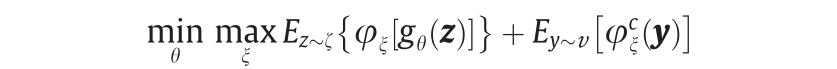
但是如果我们把成本函数换成L2 距离,那么根据Theorem 3.10,在最优情况下,Briener势能u和Kontarovic 势能能能φ是通过公式(16)的闭合式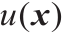 =
= 相联系的。生成器寻找到了OT映射
相联系的。生成器寻找到了OT映射 ,而判别器计算出了φ 。因此,一旦生成器达到最优解,判别器无需任何训练即可得到最优解,反之亦然。
,而判别器计算出了φ 。因此,一旦生成器达到最优解,判别器无需任何训练即可得到最优解,反之亦然。
更详细地说,假设在第k 次迭代中,生成器映射为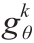 。判别器计算了Kontarovich势能φξ ,其给出了当前生成的数据分布
。判别器计算了Kontarovich势能φξ ,其给出了当前生成的数据分布 与实数据分布υ 之间的Wasserstein距离;
与实数据分布υ 之间的Wasserstein距离; 给出了从
给出了从 到υ 的OT映射。因此我们可以得到:
到υ 的OT映射。因此我们可以得到:

这意味着生成器映射可以被更新为
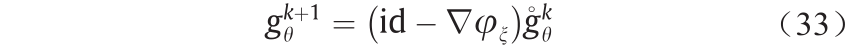
这个结论表明,原则上我们可以跳过生成器的训练过程;在实际应用中,我们通过共享中间计算结果可以大大提高计算效率。因此,在设计GAN架构时,协作优于竞争。
《5.2. 模式崩溃和正则性》
5.2. 模式崩溃和正则性
尽管GAN在许多应用中十分强大,但是它们有十分致命的缺陷。第一,GAN的训练比较复杂,其对超参数敏感以及收敛性差;第二,GAN易产生模式崩溃问题;第三,GAN可能会产生不真实的样本。不收敛性差、模式崩溃和生成不真实的样本等问题都可以通过 OT映射的正则性定理来解释。
根据Brenier的极分解定理,即Theorem 3.9,任何保测度映射都可以被分解为两个映射,其中一个是OT 映射,它是Monge-Ampère方程的解。根据正则性Theorem 3.15,如果目标测度υ 的支集Λ 具有多个连通分支,即υ 具有多个模式,或者Λ 是非凸集合,那么OT映射T : Ω→Λ在奇异点集ΣΩ上是不连续的。
图9显示了多个连通的情形,Λ 具有两个连通分支, OT映射T 在Σ1上间断。图10显示了Λ 是连通但非凸的情形。Ω 是矩形、Λ 是哑铃形、密度函数是常数、OT映射是不连续的、奇异点集合Σ1 = γ1∪γ2。
《图9》

图9. 不连续的OT映射,由基于Theorem 4.2的一个GPU算法实现生成。(a)源域;(b)目标域。(a)图中间的线代表的是奇异点集合Σ 1 。
《图10》

图10. 不连续的OT映射,由基于Theorem 4.2的一个GPU算法实现生成。(a)源域;(b)目标域。(a)图中的γ1和γ2是两个奇异点集合。
图11显示了 中两个概率测度之间的OT映射。源测度µ 和目标测度υ 均为均匀分布,Ω 的支集是单位实心球,Λ 的支集是实心斯坦福(Stanford)兔子。我们基于 Theorem 4.2计算了Brenier势能u : Ω→R 。为了可视化映射,我们按如下方式插值概率测度:
中两个概率测度之间的OT映射。源测度µ 和目标测度υ 均为均匀分布,Ω 的支集是单位实心球,Λ 的支集是实心斯坦福(Stanford)兔子。我们基于 Theorem 4.2计算了Brenier势能u : Ω→R 。为了可视化映射,我们按如下方式插值概率测度:

图11显示了插值测度ρt 的支集。表面的褶皱是奇异点集,其中OT映射是不连续的。
《图11》
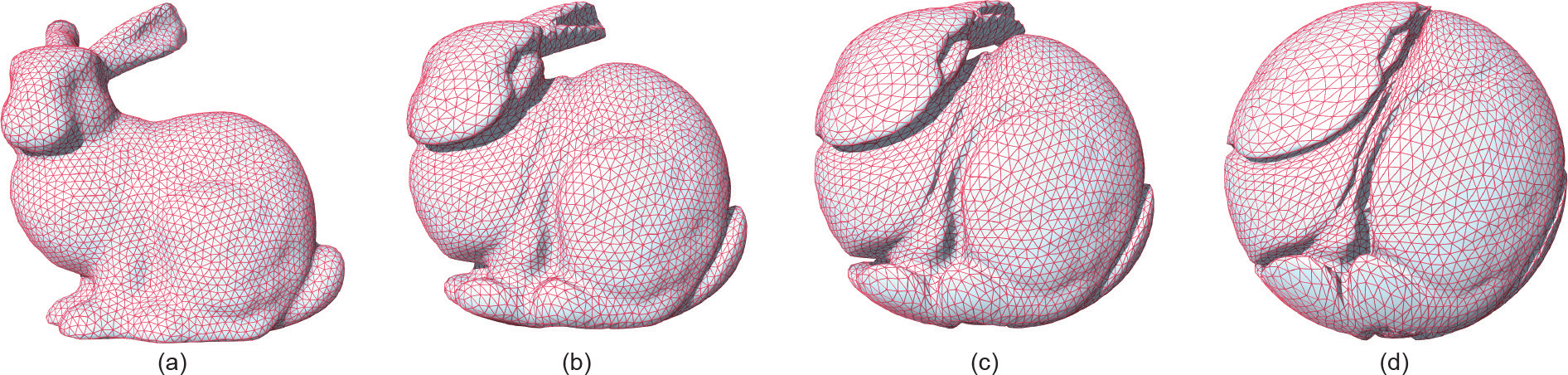
图11. 从Stanford兔子到实心球的OT映射。边界曲面上的皱褶是奇异点集合。(a)~(d)显示了变化过程。
在一般情况下,由于实际数据分布、嵌入流形Σ 以及编码和解码映射的复杂性,目标测度支集很少是凸的,所以传输映射几乎不可能整体上都连续。
另外,一般的DNN,如ReLU DNN只能是逼近连续映射。ReLU DNN所表示的函数空间不包含所需的非连续传输映射。训练过程,即搜索过程,将出现以下三种情况:
(1)训练过程不稳定、不收敛。
(2)搜索过程会收敛到Λ 的多个连通分支之一,映射会收敛到所期望的传输映射的一个连续分支。这意味着我们遇到了模式崩溃。
(3)训练过程能使传输映射成功覆盖所有模式,但同时也覆盖了Λ 以外的区域。在实际应用中,这种情况将导致GAN产生不真实的样本。如图12所示。因此,从理论上讲,直接使用DNN来近似OT映射是不可能的。
《图12》

图12. AE-OT模型生成的人脸图像。(a)生成的实际人脸图像;(b)经过奇异点的路径。(b)图中心位置处的图像的传输映射是非连续的。
《5.3. AE-OT 模型》
5.3. AE-OT 模型
如图4所示,我们将GAN的两个主要任务分为流形学习和概率分布变换。第一个任务是通过AE来计算编码映射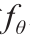 和解码映射gξ;第二个任务是利用变分方法来计算隐空间中的OT映射T 。编码映射
和解码映射gξ;第二个任务是利用变分方法来计算隐空间中的OT映射T 。编码映射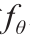 将实际数据分布υ 前推为
将实际数据分布υ 前推为 。在隐空间中,T 将均匀分布µ 映射到
。在隐空间中,T 将均匀分布µ 映射到 。
。
AE-OT模型有许多优势。寻找OT映射实际上是一个凸优化问题,这保证了解的存在性和唯一性。训练过程是稳定的,并采用了拟牛顿法进行超线性收敛。未知数的数量与训练样本的数量相等,避免了过度参数化。并行OT映射算法可以通过使用GPU来实现。OT映射的误差限可以通过Monte Carlo方法中的采样密度来控制。具有自适应性的等级分层算法进一步提高了计算效率。另外,AE-OT模型可以消除模式崩溃。
《6. 实验结果》
6. 实验结果
在这一部分,我们将展示实验结果。
《6.1. 训练过程》
6.1. 训练过程
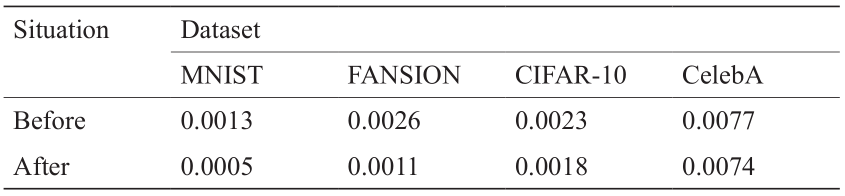
AE-OT模型的训练主要包括两个步骤,即训练AE 和寻找OT映射。正如第4节所述,使用GPU的算法实现来完成OT的步骤。在训练AE过程中,我们使用Adam 算法[49]来优化神经网络的参数,其中学习率为0.003, β1 = 0.5,β2 = 0.999。当L2 损失停止下降时,这意味着神经网络找到了良好的编码映射,我们固定编码器部分并继续训练神经网络以获得解码映射。编码器固定前后的训练损失见表1。接下来,为了找到从给定分布(我们在这里使用均匀分布)到隐空间特征的OT映射,我们从均匀分布中随机采样100N 个随机样本点来计算能量梯度。这里,N 是数据集隐空间特征的数目。实验中,θij 对于不同数据集也是不一样的。具体来说,对于MNIST和FASHION-MNIST两个数据集,θij 是0.75,但对于CIFAR10和CELEBA数据集,θij 分别为0.68和 0.75。
《表1》
表1 编码器固定前后AE的 L2 损失
我们的AE-OT模型是在Linux平台上通过使用PyTorch来实现的。所有实验均在GTX1080Ti上进行。
《6.2. 传输映射不连续性测试》
6.2. 传输映射不连续性测试
在这个实验中,我们的目的是去验证我们的假设,即在大多数实际应用中,目标测度的支集是非凸的、奇异点集是非空的以及在奇异点集上概率分布变换映射是非连续的。
如图12所示,我们使用AE来计算从CelebA数据集 (Σ, υ )到隐空间Z 的编码和解码映射,其中,编码映射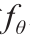 : Σ→Z 在隐空间上将υ 前推为
: Σ→Z 在隐空间上将υ 前推为 。在隐空间中,我们用第4节所描述的算法计算了OT映射,即T : Z→Z , 其中T 将单位立方体ζ 中的均匀分布映射为
。在隐空间中,我们用第4节所描述的算法计算了OT映射,即T : Z→Z , 其中T 将单位立方体ζ 中的均匀分布映射为 。然后,我们从分布ζ 中随机抽取样本z,并使用解码映射gξ : Z→Σ 将 T (z ) 映射为生成的人脸图像gξ ◦ T (z )。图12(a)展示了由该AE-OT模型生成的实际人脸图像。
。然后,我们从分布ζ 中随机抽取样本z,并使用解码映射gξ : Z→Σ 将 T (z ) 映射为生成的人脸图像gξ ◦ T (z )。图12(a)展示了由该AE-OT模型生成的实际人脸图像。
如果隐空间中前推测度 的支集是非凸的,则存在奇异点集合Σk,其中k>0。我们希望验证Σk 的存在。我们在隐空间的单位立方体中随机划上一条线段,然后沿着该线段密集插值以生成面部图像。如图12(b)所示,我们找到了一条线段γ,并生成了一个变形序列,该序列的起点是具有一对棕色眼睛的男孩面部图像,终点是具有一对蓝色眼睛的女孩面部图像。在图像中间部分,我们生成的人脸的一只眼睛是蓝色的,另一只眼睛是棕色的。这些不真实人脸图像,应该在流形Σ 之外。这意味着线段γ 穿过了奇异点集Σk,而传输映射T 在其上是不连续的,这也验证了我们的猜想是正确的,即被编码的人脸图像测度的支集在隐空间中是非凸的。
的支集是非凸的,则存在奇异点集合Σk,其中k>0。我们希望验证Σk 的存在。我们在隐空间的单位立方体中随机划上一条线段,然后沿着该线段密集插值以生成面部图像。如图12(b)所示,我们找到了一条线段γ,并生成了一个变形序列,该序列的起点是具有一对棕色眼睛的男孩面部图像,终点是具有一对蓝色眼睛的女孩面部图像。在图像中间部分,我们生成的人脸的一只眼睛是蓝色的,另一只眼睛是棕色的。这些不真实人脸图像,应该在流形Σ 之外。这意味着线段γ 穿过了奇异点集Σk,而传输映射T 在其上是不连续的,这也验证了我们的猜想是正确的,即被编码的人脸图像测度的支集在隐空间中是非凸的。
同时,我们发现AE-OT模型将训练速度提升了5倍,并且提高了模型的收敛稳定性,这是因为OT过程是一种凸优化过程。这为改进现有的GAN模型提供了一种很有前途的方法。
《6.3. 模式崩溃比较》
6.3. 模式崩溃比较
由于合成数据集由明确的分布和已知模式组成,因此利用这种数据集进行实验,可以精确地测量模式崩溃。我们选择了两个在之前的工作[50,51]中已经研究或提出的合成数据集——2D网格数据集。
关于模式崩溃测量指标的选择,我们选取了三种以前使用过的指标[50,51]。模式数量(number of modes)是指由生成模型生成的样本所捕捉到的模式个数。在这个指标中,如果在该模式的三个标准差范围内没有生成样本,则我们判定该模式已失效。高质量样本的百分比(percentage of high-quality samples)测量的是在最近模式的三个标准差范围内生成的样本比例。参考文献[51] 使用了第三个测量指标,即逆Kullback-Leibler(KL)散度。对于这个指标,每个生成样本都被分配给离其最近的模式,我们计算了被分配给每个模式的样本的直方图。该直方图形成了一种离散分布,然后我们计算了由真实数据形成的直方图的离散分布的KL散度。直观地说,该指标测量了生成样本在所有模式间关于真实分布的平衡程度。
在参考文献[51]中,作者用以上三种指标评估了 GAN [26]、ALI [52]、MD [30]和PacGAN [51]在合成数据集上的表现。每个训练实验使用的生成器都具有相同的网络结构,训练参数共约400k个。网络训练的训练样本共有100k个,迭代次数为400次。对于AE-OT实验,由于源空间和目标空间都是2D,因此我们不需要训练任何AE。我们直接计算了单位正方形上的一致分布与真实数据分布之间的半离散OT映射。理论上,OT映射恢复所有模式所需的最小真实样本数量是每个模式需要一个真实样本。然而这可能导致在插值阶段生成低质量的样本。因此,对于OT映射的计算,我们采用了512个真实样本,并根据这个映射生成了新的样本。在这种情况下,我们注意到,在OT映射的计算中只有512个参数需要被优化,并且由于Hessian矩阵的正定性,优化过程是稳定的。我们的结果见表2,其中前面使用的方法的衡量标准见参考文献[51]。我们在合成数据集上的结果和GAN、PacGAN的结果如图13所示。
《表2》
表2 2D格点数据集上的模式崩溃比较

《图13》

图13. 2D格点数据集上的模式崩溃比较。(a)GAN;(b)PacGAN4;(c)AE-OT。橙色点代表真实样本,绿色点代表生成样本。
《6.4. 与现有技术的比较》
6.4. 与现有技术的比较
我们通过实验对本文提出的AE-OT模型和其他现有生成模型进行了比较,现有生成模型主要包括Lucic等在参考文献[33]中评估的对抗模型和Hoshen、Malik在参考文献[36]中研究的非对抗模型。
出于公平考虑,我们采用了相同的测试数据集和网络架构。数据集与参考文献[31,36]中的测试数据集类似,包括MNIST [53]、MNIST-Fansion [54]、CIFAR-10 [55]和CelebA [56]。网络架构与参考文献[33]中Lucic等使用的网络架构类似。特别是,在我们的AE-OT模型中,解码器的架构和参考文献[33]中GAN生成器的架构一样,并且编码器和解码器是对称的。
我们利用FID评分[31]和PRD曲线作为评估标准来比较我们的模型和现有的生成模型。FID评分衡量了生成结果的视觉保真度,并且对图象损坏具有鲁棒性。但是FID评分对模式的添加和删除非常敏感[33],因此我们又使用了PRD曲线,PRD曲线可以量化真实数据集上模式丢失和添加的程度[32]。
6.4.1. 利用 FID 评分进行比较
FID评分计算方法如下:①通过运行inception网络 [30]来提取生成图像和真实图像中有视觉意义的特征;②利用Gaussian分布来拟合真实图像和生成图像的分布;③用如下公式计算两个Gaussian分布之间的距离:
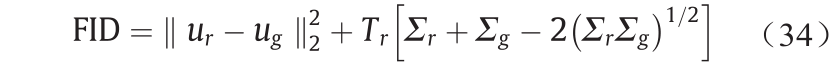
式中, 分别代表真实分布的均值和生成分布的均值;
分别代表真实分布的均值和生成分布的均值; 分别代表两个分布的方差。
分别代表两个分布的方差。
比较的结果见表3和表4,几种GAN的统计数据来自Lucic等[33],非对抗生成模型的统计数据则来自于 Hoshen和Malik [36]。一般,我们提出的模型比其他现有生成模型能够获得更好的FID评分。
《表3》
表3 用FID进行定量比较-I

The best result is shown in bold. MM: manifold matching; NS: non-saturating; LSGAN: least squares GAN; BEGAN: boundary equilibrium GAN.
《表4》
表4 用 FID 进行定量比较-II

The best result is shown in bold.
理论上来说,我们的AE-OT模型的FID评分和之前预训练的AE的FID评分接近,这从我们的实验中也得到了证实。
我们的AE采用的是Lucic等在参考文献[33]中提到的固定网络结构,它的性能不足以编码 CIFAR-10或者 CelebaA,因此我们必须下采样这些数据集。我们从 CIFAR-10中随机选择了2.5×104 张图像和从CelebaA中随机选择了1.0×104 张图像来训练模型。即使是这样,我们的模型在CIFAR-10上依然取得了最好的FID评分。由于InfoGAN模型容量的有限性,CelebA的AE性能的 FID评分(67.5)并不理想,这就使得生成的数据集的 FID评分为68.4。通过在AE架构中增加两个额外的卷积层,CelebA的L2 损失将低于0.03,而且FID评分也超过了所有其他模型(28.6,如表4括号中所示)。
6.4.2. 利用 PRD 曲线进行比较
FID评分是度量生成分布和真实数据分布之间差距的一个有效方法,但它主要用于评价精确度,它不能准确地捕捉生成模型所能覆盖的真实数据比例。参考文献[32]中的方法将分布之间的散度分解为两个部分,即精确度和查全率。
给定一个参考分布P 和一个学习分布Q,精确度可直观地衡量Q 中样本的质量,而查全率衡量了Q 所覆盖的P 的比例。
我们使用Sajjadi等在参考文献[32]中介绍的(F8, F1/8) 的概念量化了精确度和查全率的相对重要程度。图14总结了对比结果。每个点代表的是一个有超参数集的具体模型。点离右上角越近,模型的性能越好。蓝色和绿色的点分别表示了参考文献[32]中评估的GAN和VAE,黄色的点代表的是参考文献[36]中的GLANN模型,而红色的点代表的是我们的AE-OT模型。
《图14》
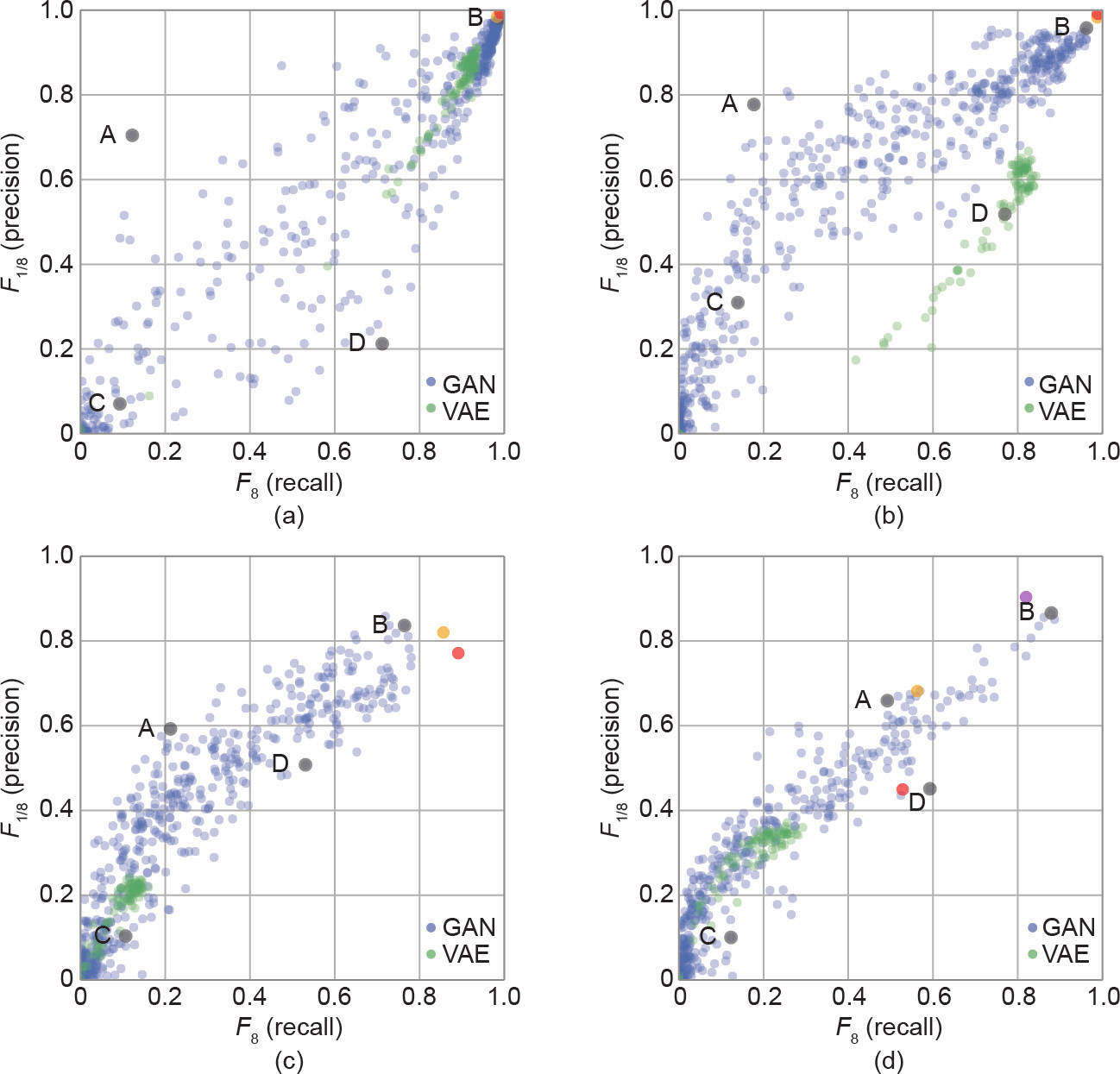
图14. 在四个数据集上,以(F8, F1/8)的精确度-查全率进行比较。(a)MNIST;(b)FASHION;(c)CIFAR-10;(d)CelebA。黄褐色的点表示参考文献[36]中的结果。红色的点是利用本文所提出的方法生成的结果。(d)中紫色的点代表添加两个卷积层后,利用本文所提出的方法生成的结果。
显然,在MNIST和FASHION-MNIST数据集上,我们提出的模型的性能要优于其他模型。对于CIFAR-10 数据集,我们模型的精确度比GAN和GLANN的稍低,但是查全率是最高的。对于CelebA数据集,由于AE容量有限,我们的模型表现得不是很可观。但是,在AE 里添加两个卷积层后,我们的模型得到了最高的评分。
6.4.3. 可视化比较
图15显示了由我们所提出的方法生成的图像和参考文献[33]中Lucic等研究的GAN以及参考文献[36]中 Hoshen和Malik研究的非对抗模型生成的图像之间的可视化的比较结果。第一列是初始图像,第二列是由AE 生成的结果,第三列是由Lucic等[33]采用GAN得到的最好的生成结果,第四列是由Hoshen和Malik采用模型生成的结果,最后一列是用我们方法生成的结果。很明显,采用我们的方法生成了高质量的图像并且该图像包含了所有模式。
《图15》

图15. 生成图像质量在 4 个数据集上的可视化比较。第一列(a)是真实数据;第二列(b)是由AE生成的结果;第三列(c)显示的是由 GAN[33]以最高的精确度-查全率(F8, F1/8)生成的结果,它对应着图14中的B 点;第四列(d)是参考文献[36]中的结果;最后一列(e)是利用本文所提出的方法生成的结果。
《7. 结论》
7. 结论
本文利用OT理论来解释GAN。根据数据流形分布假设,GAN主要完成两个任务——流形学习和概率分布变换。概率分布变换可以利用OT方法直接实现。OT 理论解释了模式崩溃的基本原因,并指出生成器和判别器之间应该是合作而非竞争的内在关系。此外,我们提出了AE-OT模型,该模型提高了理论的严谨性、增强了训练的稳定性和效率,并且消除了模式崩溃问题。
我们的实验结果验证了我们的理论推测,即如果分布传输映射是不连续的,那么奇异点集的存在会导致模式崩溃。此外,通过将我们提出的模型与现有最先进的模型进行比较发现,我们提出的模型消除了模式崩溃,并在FID评分和PRD曲线方面要优于其他模型。
未来,我们将对流形学习阶段的理论理解进行探索,并用严格的方法使这部分黑匣子透明化。
《致谢》
致谢
本项目受到国家自然科学基金项目(61936002、 61772105、61432003、61720106005和61772379)的资助。
《Compliance with ethics guidelines》
Compliance with ethics guidelines
Na Lei, Dongsheng An, Yang Guo, Kehua Su, Shixia Liu, Zhongxuan Luo, Shing-Tung Yau, and Xianfeng Gu declare that they have no conflicts of interest or financial conflicts to disclose.














 京公网安备 11010502051620号
京公网安备 11010502051620号




