《1. Introduction》
1. Introduction
It is a well-known fact that new technologies benefit society in general and national defense systems in particular. Almost every country invests significant resources into creating breakthrough technologies. The Defense Advanced Research Projects Agency (DARPA) of the United States is a government agency under the Department of Defense. DARPA makes pivotal investments with the aim of overcoming the multifaceted threats and challenges that lie ahead [1]. DARPA’s most significant achievement is its investment in computer networking technology in the 20th century. It has also contributed to many other less notable but still pivotal inventions.
Since 2004, DARPA has held a competition, the Grand Challenge, every few years. In the 2004 Grand Challenge that targeted autonomous driving technologies for driverless vehicles, only two vehicles completed the farthest distance of 11.78 km, and no winner was declared. The 2005 DARPA Grand Challenge for driverless vehicles was subsequently held, and became the best known Grand Challenge to date. In the 2005 competition, competing vehicles were required to pass through narrow tunnels and make more than 100 sharp turns over a 212 km desert route. The most challenging part of the race was a winding mountain pass with a sheer drop-off on one side and a rock face on the other, called Beer Bottle Pass.
The Urban Challenge was held in 2007, two years after the famous 2005 Grand Challenge. In this competition, the course was composed of a 96 km trip through an urban area, significantly more challenging than the course through the desert. In this Urban Challenge, participating teams were divided for the first time into two tracks, A and B. Both teams competed in the same competition, with the only difference being that track A teams were funded 1 million dollars per team. Prizes for the first, second, and third teams were 2 million, 1 million, and half a million dollars, respectively.
After this series of three Grand Challenges, the field of autonomous driving attracted more and more attention. Technologies developed for the challenges, such as sensing and navigation, have also been commercialized over many years of consecutive development. In fact, the most well-known autonomous car, the Google driverless car, is almost ready for sale [2,3]. In the meantime, more automobile producers have been integrating functions such as autonomous parking and cruising into their vehicles. Other research focuses on the vision required to recognize traffic signs, pedestrians, and other vehicles [4¯7]. From these past three challenges, we can see that the DARPA Grand Challenge programs have reformed peoples’ concepts in driving and stimulated related research in navigation and autonomous driving. Moreover, people’s lives as well as national defense systems will definitely benefit from such development in new technologies. Consequently, every DARPA Grand Challenge is now regarded as an index of future research fields. In summary, the DARPA Grand Challenge programs play an inspirational role, not only in the particular field each competition is focused on, but in the entire arena of technology.
《2. The DARPA Robotics Grand Challenge》
2. The DARPA Robotics Grand Challenge
In 2012, DARPA announced a new Grand Challenge Program focused on humanoid robots, generally called the DARPA Robotics Challenge (DRC) [8]. This is the fourth DARPA Grand Challenge in five years. The goal of the DRC is to advance the current state-of-the-art in humanoid robots.
《2.1. Background of the DRC》
2.1. Background of the DRC
In 2011, the Fukushima nuclear power plant suffered severe damage due to the tsunami triggered by the Tohoku earthquake. When the plant was hit by the tsunami, three of the plant’s six nuclear reactors melted down. Due to grave risks to human health caused by high radiation, rescue and aid workers are not expected to go into such disaster sites. The alternative is sending robots to perform a timely and effective response to minimize the impacts of such accidents. However at that time, even the most advanced humanoid robots, such as ASIMO from Honda [9], for example, would not have been able to help in the rescue. Other wheeled or tracked robots have limited traversing capabilities in the complex environment of a power plant. This historic event provided the urgency behind DARPA’s decision to push forward robotic technologies, and particularly humanoid robots.
《2.2. Why humanoid robots?》
2.2. Why humanoid robots?
Historically, DARPA has been supporting research in robotics for a long time, especially field robotics. In 1981, DARPA invested in the research and development of a six-legged walking robot called the adaptive suspension vehicle (ASV) by the Ohio State University [10¯12]. This vehicle was designed for sustained locomotion on unstructured terrain. Due to its large size and structure, it was not suitable for operation in environments originally created for human access. More recently, a four-legged robot called BigDog was developed with the support of DARPA. The goal for this robot is to carry heavy loads while traversing complicated terrains [13]. The structure and operation of BigDog are reliable and robust and it has already been equipped in the military. Again, this robot is not suitable for human-scale environments in spite of its impressive performance. It is clear that a humanoid robot, with a structure similar to that of a human being, is more suitable than other kinds of platforms in a scenario such as the Fukushima accident, since this type of environment is constructed with human size and structure in mind. Unfortunately, research in humanoid robots has not produced a robot as reliable as ASV or BigDog for operation in such hostile environments as a nuclear plant in meltdown.
Over the past 30 years, researchers have developed many humanoid robots including CURBi by Clemson University in 1986 [14], ASIMO by Honda in 2000 [15], and QRIO by Sony in 2003 [16]. Those robots are designed mostly for entertainment. For example, ASIMO can walk, run, climb stairs, and even talk with people [9]. Unfortunately, these robots are not designed to substitute for a person in performing tasks in human-made environments. However, the DRC requires humanoid robots to perform duties that are normally performed by human beings in a disaster situation, such as breaking a wall with tools, climbing a stiff ladder, traversing rough terrains, and so on. Thus the DRC will have significant influence in humanoid robot research, moving it towards realistic and useful operations rather than entertainment. For such a challenging task, the design of the humanoid robot must be more innovative and practical. Before the DRC, most humanoid robots used an electrical actuator, due to its reliable and precise performance in motion control. Boston Dynamics, however, built new humanoid robots such as Petman [17] and Atlas [18] using powerful hydraulic systems as actuators.
《2.3. Events of the DRC》
2.3. Events of the DRC
In the DRC, the competition is divided into semifinal trials and finals, running from 2012 to 2015. Like the 2007 Grand Challenge, only the six track-A teams are funded by DARPA. Moreover, seven track-B/C teams are given an Atlas robot for the competition.
To simulate the potential tasks encountered in the rescue, eight tasks are specified: Vehicle Driving, Rough Terrain, Ladder Climbing, Debris Cleaning, Door Opening, Wall Breaking, Valve Turning, and Hose Installation. Each task can score up to four points, so the total score is 32 points. Each task is given 45 min, and one intervention is allowed in case of failure. One point is available for scoring in each of the three stages of a task, and a fourth point is given if the task is completed without the intervention.
In the DRC trials held in December 2013, team SCHAFT [19] shown in Figure 1 beat all the other Atlas teams with a score of 27. The company was bought by Google after the trials. The final will be held in June 2015, with 11 teams funded by DARPA. Figure 2 shows the events making up the final.
《Fig. 1》

Fig.1 SCHAFT in the Rough-Terrain task.
《Fig. 2》

Fig.2 Eight events in the DRC final.
Out of the eight events in the competition, Wall Breaking and Hose Installation emphasize accurate hand manipulation while maintaining balance. In other events, balancing in biped locomotion is a major challenge. Some teams designed robots with different structures, such as CHIMP [20] that uses tracks for motion, and RoboSimian that uses four legs for walking [21]. The purpose of such a design is to avoid the challenges of biped locomotion. Other participating robots, like SCHAFT and Atlas, have to prevent themselves from falling in various kinds of environments. Consequently, Rough Terrain is the most crucial task for all teams using a humanoid structure. As members of the team DRC-HUBO, we are responsible for rough-terrain walking. To deal with these stability challenges, we propose a different approach, the Ski-Type gait, which we describe in the next section.
《3. The birth of the Ski-Type gait》
3. The birth of the Ski-Type gait
Some of the teams in the DRC designed their new robot specially for the competition, while our team has focused on a gait and algorithm design to enable the existing platform to accomplish the events. In this section, we briefly introduce the platform and our development of the Ski-Type gait.
《3.1. Introducing our robot》
3.1. Introducing our robot
The humanoid robot platform of our team is HUBO2, a full-sized humanoid robot developed by the Korea Advanced Institute of Science and Technology. It has 40 degrees of freedom, weighs 45 kg and is 1.25 m tall. It has two force/torque sensors on each ankle joint and an inertial measurement unit on the waist. In summer 2013, its motors were upgraded to be more powerful and its arms were enlarged for better hand manipulation, resulting in DRC-HUBO, shown in Figure 3.
《Fig. 3》

Fig.3 HUBO2 (left) and DRC-HUBO (right).
《3.2. Core strategy for balancing on rough terrain》
3.2. Core strategy for balancing on rough terrain
By reviewing the literature, we determined that applying controllers to balance a humanoid robot is the most popular approach. Basically, this approach relies on the sensing of contact conditions and the state of the robot to tune configurations. However, on a rough terrain that is slippery and that deforms upon pressure, such control cannot usually provide a satisfying performance. To improve the balancing capability of our humanoid robot, we presented the strategy of enlarging the supporting area. In the following sections, we discuss various ideas towards realizing this goal.
《3.3. Enlarging the foot pedals》
3.3. Enlarging the foot pedals
Our first attempt was to enlarge the foot pedals, as this would obviously enlarge the supporting area. However, the disadvantages of this strategy are numerous. Firstly, the width of the foot pedals cannot be increased significantly; otherwise, the pedals will step on each other without moving forward. Thus increasing the length of the foot pedal is the only option.
Unfortunately, a lengthened foot pedal increases the torques on the lower body joints while walking. Moreover, clearance will be at risk with a long foot pedal, since a collision is more likely to occur when stepping over obstacles, and this would be fatal to the system. Another disadvantage is that a larger foot pedal requires more landing space on the ground, introducing more complexity in foothold planning.
Based on the analysis above, we gave up the approach of enlarging the foot pedals. We believe that the mechanical design of the robot should not be changed even if the supporting area needs to be increased. Since multiple-legged robots usually have much better stability performance than biped robots, we next examined the feasibility of turning our humanoid robot into one with quadruped-mode locomotion.
《3.4. Quadruped walking》
3.4. Quadruped walking
In biped walking, the only supporting area while taking steps is one foot pedal, which limits the stability performance. On the other hand, quadruped walking enables as many as three points to touch the ground in a gait cycle. In this way, the supporting area is enlarged more efficiently than by enlarging the foot pedals. To perform quadruped walking, there are two possible solutions: leaning forward and leaning backward (Figure 4).
In our early experiments on HUBO2, we attempted to make HUBO2 bend backward for quadruped walking. When the legs folded heavily, the arms could touch the ground. However, the folded legs limit the locomotion capability. As a result, we went back to leaning the torso forward with unfolded legs, as depicted to the left in Figure 4. The short arms, however, still could not touch the ground [22]. In addition, the delicate design of the hands did not allow any contact with the ground, let alone supporting the body.
《Fig. 4》

Fig.4 HUBO2 forward quadruped (left) and DRC-HUBO backward quadruped (right).
In DRC-HUBO, the arms were extended and we suggested the addition of a spike on each hand, to touch the ground without damaging the hand. Backward quadruped walking is tested on the right in Figure 4. On a flat surface, this quadruped walking worked well; however, the heavy torque on the arms frequently caused system failure after around 20 min of operation. Moreover, the torso was much lower than in biped walking and the step clearance was limited. In our test of stepping over wooden bars, collision was unavoidable in the case of a 20 cm square bar.
As shown by these attempts, the DRC-HUBO performing quadruped walking still did not meet our expectations. Instead, we proposed the use of some tools to aid walking, rather than making permanent changes to the mechanical design. We chose the Ski-Type gait as a way to realize quadruped walking.
《3.5. The Ski-Type gait》
3.5. The Ski-Type gait
In real life, people usually hold a trekking pole to assist their legs while climbing mountains. Similarly, older people use a cane to augment leg strength in walking. Based on these observations, we came up with the idea of the Ski-Type gait, shown in Figure 5. Research exists on developing robots to function as a cane for walking assistance (a cane-robot) [23¯26]. In our work, however, the cane is an ordinary stick held by a robot hand to assist walking, and is not a robot.
《Fig. 5》

Fig.5 Ski-Type walking concept.
To perform the Ski-Type gait, the robot holds two canes, one in each hand. Given the robot’s redundant arm and hand joint, using the canes to touch the ground is feasible, and the gait becomes quadruped. Although the wrist joint is not very powerful due to the small motor size, redundancy allows us to distribute the torques among the arm joints to respect such limits. In the Ski-Type gait, the arm can be viewed as a 3-link limb, while the leg is considered a 2-link module (foreleg and thigh). Thus this gait becomes a special case of quadruped walking. However, it bears many advantages in addition to the stability provided by quadruped walking.
First of all, humanoid robots are usually required to perform manipulating tasks. That is, their hands must hold tools for this purpose, as in the case of the Wall Breaking and Hose Installation events. Consequently, frequent transitions between quadruped and biped states are required. In either forward or backward quadruped walking, a transformation into biped standing has a huge energy cost. However, with the use of canes, the Ski-Type gait can facilitate a simple transition to enable hand functions. The canes can simply be dropped when the hands need to perform a manipulating task, and then grasped again when the robot needs to negotiate difficult terrains. The robot may still gain some stability even if one hand manipulates while the other holds a cane.
Another benefit of the Ski-Type gait lies in the flexibility of where the hands hold the canes. Holding on at different places changes the effective cane length, which is equivalent to variation in the robot “leg” structure. Such flexibility enables the robot to transform to different configurations when dealing with different scenarios. One example is the height of the center of mass (COM). For long canes, the COM is high, and the robot is able to ensure a large clearance from the ground. Short canes, on the other hand, enable a low COM, which provides better stability at the cost of small clearance.
From the discussion above, we conclude that the Ski-Type gait is a simple and effective solution to meet the challenges of difficult terrains, while requiring almost no modifications to the original structure of the humanoid robot and providing more flexibility and stability in the gait.
《4. Stability analysis of the Ski-Type gait》
4. Stability analysis of the Ski-Type gait
In our search for possible approaches to increase the supporting area, we have proposed the Ski-Type gait. In this section, we model and analyze the stability performance with stabi-lity margin as the criterion. The robot model is based on the HUBO2 platform.
《4.1. Assumptions in the modeling》
4.1. Assumptions in the modeling
In the Ski-Type gait, there are numerous configurations available for planning the leg and cane motions because of the redundancy. However, based on our experience with HUBO2 and experiments of human beings performing the Ski-Type gait, we model the top view of our chosen gait for stability analysis, as shown in Figure 6.
《Fig. 6》
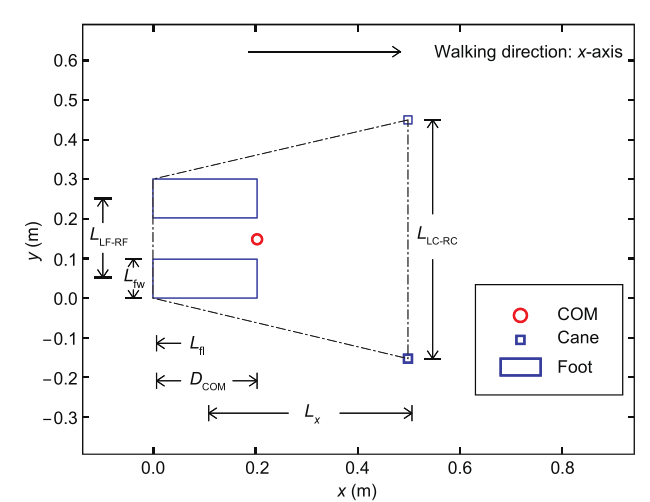
Fig.6 Ski-Type gait modeling, top view.
In this configuration, we place the COM on the front edge of the foot pedals. This is to shift the COM towards the back of the supporting area in the initial posture. The purpose is to let the legs sustain more weight than the canes, since the legs are more powerful than arms. Such an arrangement can prevent potential damage to the arms.
Another consideration is the sequence of the COM “shift.” In traditional quadruped walking, there is no obvious difference between arms and legs, and the COM moves forward whenever a limb swings forward [27]. In the Ski-Type gait, we place the COM near the feet. If the COM moves when the arm is in motion, the force/torque on the other supporting arm will significantly increase, which may damage/crash the arm. So we shift the COM only when the leg is in motion. This consideration provides an additional benefit: When the canes are equipped with sensors for detecting the terrain for a solid touching, the risk of a fall can be reduced, because there is no COM shift in the process. Moreover, we assume no lateral COM sway throughout the gait. This is possible because the supporting area is enlarged by adding the canes, as opposed to biped locomotion, in which the COM shifts laterally to maintain support by the landed leg. Eliminating lateral sway also reduces energy consumption by the robot.
《4.2. Step sequence choice》
4.2. Step sequence choice
Step sequence is the next factor to be determined in designing the Ski-Type gait. Since we propose to perform quasi-static walking, the gait should be crawl-like. If the leg moves following an arm motion on the same side, the gait is called Crawl-1; if on the opposite side, it is called Crawl-2 [28]. To determine which of these two gaits is preferable, we calculate their minimal stability margin ( Smin) in a walking cycle under the same initial configurations and step length.
As seen in Figure 6, the parameters affecting the stability are:
Lfw: The width of the foot pedal;
Lfl: The length of the foot pedal;
LLF-RF: The length between the centers of the two foot pedals along the y-axis;
LLC-RC: The length between the two cane tips along the y-axis;
DCOM: The length between the COM and the cane tips along the x-axis in the initial posture (according to the assumption for the position of the COM, DCOM= Lfl);
Lx: The length between the cane tips and the center of the foot pedal along the x-axis;
Lstep: The step length.
Because of the lateral symmetry in the Crawl-1 and Crawl-2 gaits, the supporting area and the COM position are shown for only one half of the cycle. To obtain a numerical result, values must be assigned to the variables. Based on the mechanical dimensions of the HUBO2 robot, we set Lfw= 0.1 m and Lfl= 0.2 m [29]. Based on our experiments of a human walking with two canes, we obtained a sense of how far to reach out the canes, how widely to separate the canes, and what to use as the step size. Next based on the height of HUBO2, we set the following parameters to be the nominal values for the Ski-Type gait: LLC-RC= 0.6 m, DCOM= 0.2 m, L x=0.4 m, and Lstep= 0.2 m.
Figure 7 shows the COM and the supporting polygon when the right cane moves and then the right foot swings for Crawl-1. Figure 8 shows the COM and the supporting polygon when the right cane moves and then the left foot swings in Crawl-2. To assist our description, we name the supporting edge formed by the cane tips the “TT-Line,” and the edge on the right formed by the cane tip and the foot the “TFR-Line.” By checking the COM and the supporting area, we conclude that change in the TT-Line does not affect the stability margin, since the COM is positioned far from the canes. However, the TFR-Line is the edge closest to the COM, meaning that it is the most crucial edge affecting the stability.
《Fig. 7》

Fig.7 Ski-Type gait for Crawl-1.
《Fig. 8》

Fig.8 Ski-Type gait for Crawl-2.
In the two Smin graphs (Figure 7(f) and Figure 8(f)), there are obvious jumps when the end-effectors (canes and foot pedals) swing. These jumps are the result of a sudden change in the shape of the supporting polygon. In both Crawl-1 and Crawl-2, when the right cane swings forward, the stability margin is minimal. This result agrees with our observation that the TFR-Line has the most significant effect on Smin. In Crawl-1, the TRF-Line is much more inclined than in Crawl-2. Thus, the supporting polygon of Crawl-1 results in a smaller stability margin.
Through this analysis, the Crawl-2 step sequence outperforms Crawl-1; it results in greater Smin, and thus provides better stability for the robot. This conclusion is different from the optimal step sequence described in Ref. [27], in which the arms are treated as legs and all four points of contact are treated as point-contacting. In this case, our humanoid robot has foot pedals, and only the cane tips can be viewed as points. Therefore, we conclude that Crawl-2 is the better step sequence for the Ski-Type gait under this configuration.
《5. Force/torque analysis for the Ski-Type gait》
5. Force/torque analysis for the Ski-Type gait
In this section, we analyze the force/torque distribution in the Ski-Type gait. Since many different walking patterns are possible in terms of speed and foothold positions, we perform a general analysis on the initial posture. Because of the symmetry of the initial static posture, we ignore the force/moment components around the x-axis. Figure 9 shows the modeling for the force/torque analysis. The points from O to E represent the ankle, knee, hip, shoulder, elbow, and wrist joints, respectively. Point F is the contact point of the cane tip with the ground. Thus, a closed-chain system is formed.
《Fig. 9》
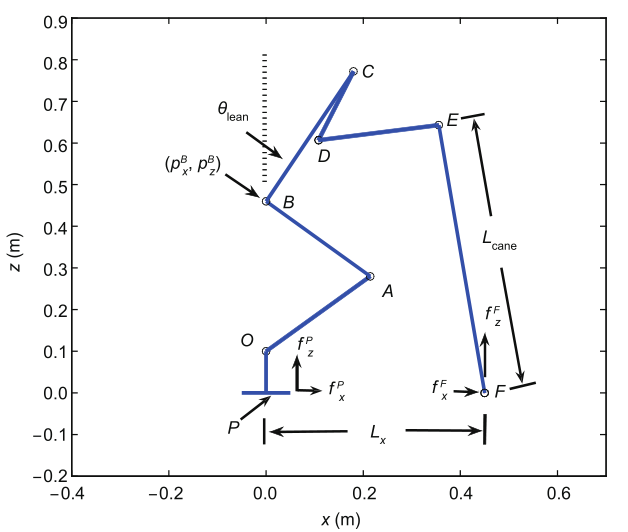
Fig.9 Variables for force/torque analysis.
《5.1. Foot pedal contact model》
5.1. Foot pedal contact model
There are three types of contact conditions including hard-point contact with friction [30], soft-finger contact, and rigid contact [31]. Hard-point contact with friction indicates that a reaction force normal to the contact surface and two friction forces exist, but no moments. Soft-finger contact and rigid contact allow for one or three moments, respectively, along with the three forces. In our case, we choose the hard-point contact model for the foot-pedal contact. To assist our description, we introduce an effective contact point P as shown in Figure 9. Figure 10 shows a zoomed-in view of the foot pedal following the hard-point contact model. Since the effective contact point P can be anywhere along the foot pedal, the distance from P to the rear end of the foot pedal should be less than or equal to the foot pedal length. To be stable, the point P should be supported by the terrain.
《Fig. 10》

Fig.10 Hard-point contact modeling for the foot pedal.
Parameters for analyzing force/torque distribution
Based on Figures 9 and 10, the parameters for analyzing the force/torque distribution in the initial posture are:
( PxB, PzB): The position of the hip joint;
θlean: The angle between the torso link and the positive z-direction;
Lx: The length between the cane tips and the center of the foot pedal along the x-axis;
Lcane: The cane length;
LP: The distance from the ankle joint to the effective contact point Palong the x-axis;
( fxF, fzF): The contact force at the cane tip;
( fxP, fzP): The contact force at the effective contact point P on the foot pedal;
μ: The static friction coefficient;
m: The total mass of the system;
g: The gravitational acceleration.
As illustrated in our previous work, parameters (PxB, PzB), θlean, Lx, and Lcane will significantly affect the valid motion pattern in the Ski-Type gait, resulting in different stability performances. In our force/torque distribution analysis, these parameters are also crucial variables. The remaining parameters ( fxF, fzF), ( fxP, fzP), and L P are used to describe the solution of the force/torque distribution.
The final issue before the analysis is the physical values of the links. For consistency with our previous work, the mass and length of each link, as well as the joint torque limits, are based on the HUBO2 humanoid robot available in our laboratory.
《5.3. Determining the joint torques》
5.3. Determining the joint torques
For the closed-chain system, the joint torque solution is not unique, due to the redundancy. At the initial posture, we have the following equations:
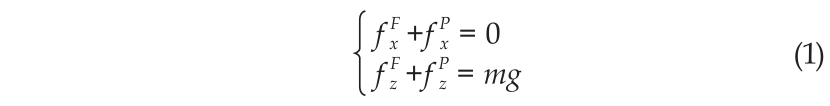
which are satisfied regardless of the position of the effective point P. Consequently, if the force pair ( fxF, fzF) is a variable, the joint torques will vary correspondingly. For the sake of generality, ( fxF, fzF) will be scaled by mg and expressed as a ratio.
For fzF, the minimum is 0 because the contact point cannot provide force pointing downwards without a hinge. The upper bound ratio is set at 1, since the foot pedal is not hinged either. Moreover, the force pair should follow the friction constraint. In summary:

Another constraint is that the effective point P should lie within the foot pedal, so that | LP|≤ Lfl. Also, each resulting joint torque must be within the limits, since the joint torques depend on the value of ( fxF, fzF) in the system equations. To obtain an optimal solution, we choose to minimize the total torque required. For the posture shown in Figure 9, the total torque is minimized when the cane forces are ( fxF, fzF)=(–0.042 mg, 0.202 mg) and μ=0.6, so the corresponding joint torques are within the limits.
《6. Implementation of the Ski-Type gait》
6. Implementation of the Ski-Type gait
At the start of the Rough Terrain task, there are several wooden bars for the robot to step over. To avoid collision with such obstacles, a certain step size is necessary. In our Ski-Type gait, having three contacting points while taking steps limits the available step size, due to the kinematic constraints on the gait. Since the cane length directly changes the kinematic structure, we need to determine the cane length in regards to the available step size. To do so, we also need to consider the trajectory of the foot and the cane tips. We assume the curve governing their motion trajectories to be sinusoid for smoothness in both position and speed. It can be modeled as follows:
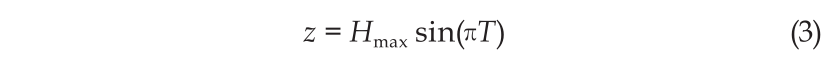
where Hmax is the maximum lifting height in one step; T stands for the total time of one step; and z is the height of the foot pedal or cane tips. Moreover, we assume the foot pedal to be leveled to ensure ground clearance. This sinusoid trajectory pattern is also available on the HUBO2 platform.
《6.1. Variables in cane-length selection》
6.1. Variables in cane-length selection
Figure 9 defines and shows the parameters for configuring the Ski-Type gait in the force/torque analysis. In this section, we also make PxB=0 and introduce θankle to determine the hip position. Since the thigh and leg are the same length, the hip joint is always over the ankle joint. In conclusion, we fix the following parameters for determining the step size and the corresponding cane length as shown in Figure 11.
《Fig. 11》
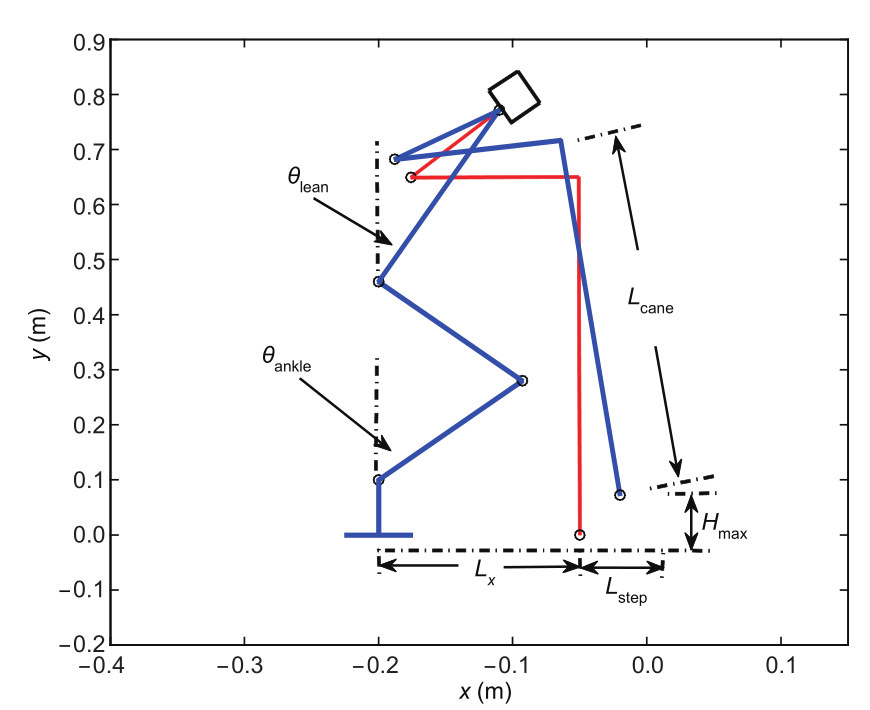
Fig.11 Variables for cane design.
θlean: The angle between the torso and the y-axis; this can be used to tune the COM position with respect to the supporting area;
θankle: The angle between the leg and the z-axis;
Lcane: The cane length;
Lx: The length between the cane tips and the center of the foot pedal along the x-axis;
Lstep: The step length;
Hmax: The maximum lifting height in one step.
《6.2. Relationship between Lcane and Lstep》
6.2. Relationship between Lcane and Lstep
To determine the valid step size in the Ski-Type gait, we introduce an inverse kinematic (IK) solver to calculate the joint values. Once the cane length and the step pattern are fixed, the IK solver provides the joint values throughout one step. If the joint values are all within the limits, the corresponding step size is feasible with that cane. According to the dimensions of HUBO2, the joint limits are set to be:
Ankle pitch: 0° to 88°
Knee pitch: 0° to 160°
Hip pitch: 0° to 88°
Shoulder pitch: −90° to 90°
Elbow pitch: 0° to 170°
To determine the step size range for each corresponding cane length, some of the variables need to be assigned. We set θlean=30° and Lx=0.30 m. For each fixed cane length, the step size increases and the trajectory follows Eq. (3). The maximum step size is calculated with each corresponding cane length. We also check the relationship under three different conditions, where the ankle joint values are 20°, 30°, and 40°, respectively. Figure 12 shows the results, followed by a few observations.
《Fig. 12》

Fig.12 Relationship between Lcane and Lstep under three configurations.
•As θankle decreases, the COM height increases, and the reasonable Lstep range shifts to the right; meaning that longer canes are needed to take steps.
•When θankle decreases, the maximum achievable step length decreases. Moreover, when θankle = 20 ◦, the curve flattens around Lcane = 0.80 m. This flattening happens when the COM is relatively high and Lcane is large enough. Previously, we assumed that the canes touch the ground vertically. However, the arms of HUBO2 are short and the elbow joint cannot bend backward because of mechanical constraints in the design. So Lstep cannot increase once the canes become longer than about 0.80 m.
•To the far right of each curve is a steep drop. The reason for this drop is that in such ranges, the elbow joints are heavily bent when in the initial position. Consequently, the canes cannot be lifted to follow the sinusoid curve, as they are limited by the elbow joint constraint.
Based on the results in Figure 12, we choose Lcane = 0.75 m for the following reasons. Firstly, as θankle changes, the height and valid Lstep range change accordingly. The Lcane value of 0.75 m promises a large step size for all three scenarios of θankle. Secondly, 0.75 m is around the height of the torso, making this a comfortable posture for the HUBO2 robot to hold the canes.
《7. Simulation and experiment》
7. Simulation and experiment
To validate our design of the Ski-Type gait, we performed a simulation using the OpenRAVE simulator, a robot simulator developed by Rosen Diankov of the CMU Robotics Institute. Based on OpenRAVE, Robert Ellenberg from Drexel University developed supplementary packages for simulations dealing with the HUBO2 model [32]. The simulator involves a physics engine for dynamics; therefore, the result is close to real-robot operation. Figure 13 shows snapshots of the simulation, in which the HUBO2 robot performs the Crawl-2 Ski-Type gait. Based on the result of the cane length design, we attach two 0.75 m canes to the robot hands.
《Fig. 13》

Fig.13 HUBO2 Ski-Type gait on flat surface in OpenRAVE.
After the simulation, we performed experiments on grass. The softness and slipperiness of the grass constitute one kind of rough terrain condition, so grass is an ideal test for the stability performance of biped and Ski-Type gaits. In our analysis, we assumed no lateral sway in the Ski-Type gait. Through our experiments, however, we found that adding the lateral sway alleviates the arm torque on the side of the swinging leg, reducing the possibility of system failure due to limited torque. Thus, we introduced the same lateral sway in Ski-Type as in biped walking for better comparison.
Figure 14 shows the experimental result of biped and Ski-Type gaits. In biped walking, the COM sways left and right to maintain balance while taking steps. When HUBO2 sways to its right with the left foot swinging in the air, the grass under the right foot pedal is compressed because of the pressure, and the foot pedal tilts to its right. Consequently, the actual COM position differs from the reference COM position, which makes Smin smaller. Since the motion is open-loop, the COM error cannot be killed and HUBO2 will sway to the other side. As a result, oscillation of the COM occurs as HUBO2 takes steps, as shown in Figure 14. After three steps, HUBO2 falls because of the oscillation.
《Fig. 14》

Fig.14 HUBO2 biped and Ski-Type gait on grass.
In the Ski-Type gait, on the other hand, the supporting area is not just composed on the foot pedals. Because it involves using the cane tips and foot pedals alternately, the supporting area is much larger. When HUBO2 sways to the right, Smin still decreases because of the deformation of the grass, but the Ski-Type gait provides much greater Smin values to ensure stability. Furthermore, the three supporting points form a triangle, which will prevent the oscillation from growing. In addition, the shared weight causes less deformation under the foot pedals, and COM disturbances are smaller compared with the biped gait. These experimental results verify that the Ski-Type gait is more stable than the biped gait.
In the 2013 December DRC trials, our upgraded DRC-HUBO was more powerful with extended arms. Since the surface of the terrain setting was solid and flat, we adopted bipedal walking for fast motion and successfully passed the up-and-down ramps, as shown in Figure 15. However, the robot fell before the zig-zag hurdles and ran out of time for the second trial [33].
《Fig. 15》

Fig.15 DRC-HUBO on Rough Terrain in DRC trials.
《8. Conclusions and future work》
8. Conclusions and future work
We developed the Ski-Type gait for humanoid robots for the Rough-Terrain challenges in the DRC. The Ski-Type gait ensures a larger supporting area compared with biped walking, and provides more flexibility than quadruped walking, due to different holding places on the canes changing the whole body posture. In our stability analysis of the Ski-Type gait, stability margin was the criterion. We compared two different step sequences, Crawl-1 and Crawl-2, under the same configurations. Then we performed a force/torque analysis for the initial posture. For the closed-chain system, the joint torque solutions were multiple because of the redundancy. So we chose to minimize the total torque to fix a unique solution.
Moreover, we implemented the Ski-Type gait on the HUBO2 platform by designing the cane length. Since cane length determines the kinematic structure and thus affects the motion capabilities, we checked the maximum step length for stepping over wooden-bar obstacles to determine the cane length. From our simulation and experimental results, the Ski-Type gait is proved smooth on flat floors and on grass. In our future work, we will analyze the force/torque distribution throughout the walking cycle to study the characteristics of the joint torques. Then we will investigate strategies for choosing the values for various parameters by considering the stability, energy consumption, and motion capability as a whole.
《Compliance with ethics guidelines》
Compliance with ethics guidelines
Hongfei Wang, Shimeng Li, and Yuan F. Zheng declare that they have no conflict of interest or financial conflicts to disclose.













 京公网安备 11010502051620号
京公网安备 11010502051620号




