《1. Introduction》
1. Introduction
Proliferation in the manufacturing of complex products has exacerbated resource consumption and environmental pollution, further stressing out the Earth’s ecosystem. For example, global greenhouse gas (GHG) emissions continued to rise until 2018 [1]. In 2019, worldwide carbon emissions totaled 33 billion tons, a slight slowdown in growth [2]. In complex product manufacturing, ferrous metal smelting and processing are the major contributors to GHG emissions, with a 35.9% share [3]. Hydraulic presses are a staple in metal forming processes owing to their ability to deliver high pressure forming [4,5]. However, they are also typically complex products that result in high energy and material costs during their manufacturing. In 2013, China produced approximately two million metal forming presses [6]. The growing demand for energy and material resources may cause irreversible damage to the environment. Hence, this study focuses on the design optimization of complex products, balancing performance and resource saving metrics, using a hydraulic press as an optimization case study.
Many researchers have explored optimization methods regarding hydraulic presses to reduce resource costs and alleviate environmental pollution. These optimization methods have mainly concentrated on the efficient usage of, for example, the drive system [7–12] and reasonable structural design. Compared with traditional drive system optimization, the structural optimization of machinery is crucial for saving resources and reducing consumption. Structural optimization focuses on the size, weight, layout, and so forth, of the entire machine and its parts. Among these, the lightweight design optimization of a hydraulic press not only saves resources but also improves the performance of the hydraulic press. With respect to satisfying reliability requirements, a larger weight of the hydraulic press means a greater cost in terms of metallic material. Furthermore, heavy hydraulic presses have large inertia and tend to consume more fuel during transportation or processing. However, reasonable weight reductions can increase the natural frequency of the support while guaranteeing constant stiffness, which results in reduced vibrations and better load bearing of the hydraulic press. Therefore, it is important to correctly determine the support material, wall thickness, cross-sectional shape, and size to manufacture the ribs reasonably. Strano et al. [13] optimized the design process with respect to energy efficiency. Li et al. [14] adapted an effective topology optimizer for hydraulic presses to reduce GHG emissions and enhance their structural performance in manufacturing. Liu et al. [15] used an explicit topology optimization method to improve the lowcarbon casting of a hydraulic press slider.
In a hydraulic press, the support plays an important role in ensuring safe and stable work. It considers the plate structure formed by the tailored welding or casting of discrete plate units as a ground structure. The plate structure has the advantages of a simple structure, ease of manufacturing, and a high bearing capacity. In the current structural design optimization of plate structures, most plates are optimized by changing the dimensional parameters within the existing plate layout. This design optimization aims to reduce the weight of the structure, but has limited effectiveness. Compared to topology optimization, size optimization of individual components has less design freedom and cannot significantly lower weight in a limited area. Here, we propose a collaborative topology optimization method that simultaneously changes the number of plate units and optimizes their sizes. In contrast with the contemporary method that obtains the determined plate structure layout through experience, our novel method can simultaneously reduce the overall weight and improve the support stiffness of the plate structure effectively.
The design objectives of the topology optimization are the plate thickness parameters and topological variables. These objectives can be solved using a mathematical model based on a truss-like structure. In previous studies, many researchers have investigated applicable methods for optimizing a truss-like structure. The finite element method (FEM) has been improved by researchers as an effective traditional optimization method. They used FEM to analyze the frame structure, as well as to test and evaluate the optimum design parameters [16–19]. Many studies have focused on the performance of structural characteristics, apart from the optimization method. Lan et al. [20] considered three aspects—topology, shape, and size—to optimize the design of a fine-blanking press frame. Yan et al. [21] studied the characteristics of the heavy load-bearing frame of a hydraulic press based on the finite element optimization method, which enabled them to simultaneously increase the stiffness of the frame and lighten the structure. The above studies all performed topology optimization without considering uncertainties. However, ignoring uncertainties may result in the unreliability or even failure of the structure.
In an actual engineering structure, parameters such as the applied loads, material parameters, and structural geometry inevitably contain uncertainties owing to the influence of manufacturing and various environmental factors. The topological structure derived from deterministic topology design optimization may violate these constraints and fail to meet the performance requirements of the design. Thus, it is necessary to consider uncertainties and use an appropriate model to judge the reliability of the optimized structure. Liu and Moses [22] and Thampan and Krishnamoorthy [23] initially introduced reliability as a constraint in the single-objective topology optimization of a truss. Subsequently, many researchers have begun to consider the impact of uncertainties on reliability. A probabilistic method was proposed to express uncertainty parameters in the form of a normal distribution, taking structural performances as objectives, and the probability of failure as a constraint for reliability-based topology optimization [24]. In a study by Greiner and Hajela [25], the uncertainties of the external load and yield stress were represented as Gaussian normal distributions, and the structural mass and reliability were the objectives for the truss topology optimization. Jalalpour et al. [26] researched the geometry and material uncertainty of a truss and proposed a stochastic stiffness reliability topology optimization model. Torii et al. [27] proposed a probabilistic approach for simultaneously optimizing the geometry and topology of trusses, considering the uncertainties in the applied forces and yield stresses. Furthermore, many non-probabilistic methods have been developed to minimize various types of uncertainties in reliability-based structural topology optimization. These non-probabilistic uncertainties are mainly expressed in uncertainbut-bounded (interval or convex) sets [28,29] or fuzzy sets [30]. There are also uncertainties of different types mixed into one reliability problem, which lead to the probabilistic–non-probabilistic hybrid reliability analysis method [31–33], and other mixed forms. Non-probabilistic and hybrid methods have expanded the solution to uncertain problems. Considering the practical problems comprehensively, in this study, we chose the probabilistic model to study stochastic uncertainties.
According to these past studies, two problems are worth pondering upon. First, the coupling of the reliability analysis of uncertainties and topology optimization may lead to an inefficient solution process. Second, the reliability topology optimization model built based on uncertain parameters may not be well suited to the teaching–learning-based optimization (TLBO) algorithm. This would have a detrimental effect on the convergence speed and accuracy of the algorithm. In this study, some innovations were made to alleviate the above problems. First, the probability distribution of uncertain parameters is determined in practical engineering. In the reliability analysis stage, the probability of failure is converted into a reliability index constraint. Second, the uncertain parameters are modified into deterministic parameters based on their reliability. We also decoupled the previous complex optimization process into a topology optimization process and a deterministic reliability analysis process. The decoupled model is suitable for parsing the algorithm and improving optimization efficiency. Third, we selected the TLBO algorithm to solve for the design variables. We improve the algorithm by adopting the adaptive teaching factor to make the convergence rate faster in the initial search stages, and to make the search more refined after a certain number of iterations.
The remainder of this paper is organized as follows. In Section 2, the characteristics of the structure are studied, and a topology optimization model is built. Section 3 discusses the model analysis with uncertain parameters based on reliability. Section 4 introduces the solution process of the TLBO algorithm in detail. An example of the optimization results is provided in Section 5, followed by the conclusions in Section 6.
《2. Hydraulic press support plate system optimization model》
2. Hydraulic press support plate system optimization model
This section summarizes the typical structure of a hydraulic press support and presents the optimization model.
《2.1. Ground structure approach》
2.1. Ground structure approach
To perform structural topology optimization, the entire structure needs to be divided into design domains for research. There are two types of design domains: ground and continuum structures. The ground structure approach is a common method used to study discrete structural topology optimization, which is well suited to our research objectives. The basic idea is to construct an exhaustive set of discrete structural elements (truss or beam/ frame elements) in the design domain. A ground structure composed of a truss structure is shown in Fig. 1. The design variables are the section parameters of these units, such as area and thickness, and whether these units exist. The goal of topology optimization is achieved by removing some units from the original exhaustive set of units in the design process [34].
《Fig. 1》

Fig. 1. Ground structure of a truss. P: the external force applied to the truss.
The box-type plate structure of the hydraulic press support is composed of interlaced and interconnected plate elements. The connection mode between the units is a rigid consolidated plate. The plate units are divided into three parts for different functions, including the carrier plate, force transmission plate, and closed plate. As shown in Fig. 2, the upper part of the box-type plate structure is a carrier plate, where an external load is applied. The force transmission plate in the middle is perpendicular to the carrier plate that transmits the loads. The topology optimization discussed in this paper is mainly aimed at the size and topology variables of the force transmission plate. The bottom is a closed plate that closes the overall structure together with the carrier plate and force transmission plate to form a cavity structure.
《Fig. 2》

Fig. 2. Composition of a plate system. t: the given carrier plate thickness; q0: external load; Lx: the spacing between the force transmission plate; uy: local displacement.
When constructing the ground structure of the box-type plate structure, it is necessary to limit the local displacement uy at the center of the cavity. This limitation prevents the unreasonable spacing of the ground structural plates from causing excessive displacement of the carrier plate. For a given carrier plate thickness t, the spacings Lx and Ly of the force transmission plate are specified. The displacement uy at the center of the carrier plate and external load q0 have a monotonically increasing relationship. The displacement uy is larger when the external load q0 increases, and the displacement reaches the permissible value [uy] when q0 is sufficiently large. Accordingly, the plate spacings Lx and Ly, corresponding to [uy], are the permissible maximum plate spacings.
《2.2. Topology optimization model of the plate structure》
2.2. Topology optimization model of the plate structure
The plate structure of the hydraulic press support is forcesupporting. Its design requires sufficient stiffness to satisfy the loading requirements while ensuring the lightest possible structure. Thus, this is a multi-objective topology optimization problem. After determining the ground structure of the hydraulic press support, we introduce the topological variable r = [ r1,r2, …,rn ]T and plate thickness variable t = [ t1,t2,… ,tn] T , where n is the number of plates, T is matrix transpose. The topological variable indicates whether the plate exists. When the topological variable is set to zero, the plate thickness variable is also set to zero. By considering both variables simultaneously, the coupling between the topological variable and plate thickness variable in the topology optimization is solved. The total weight of the plate structure can be expressed as follows:

where ρ is the material density, ri is the topological variable of the plate (ri 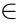 { 0, 1}) , Ai is the area of the plate, and ti is the thickness of the plate.
{ 0, 1}) , Ai is the area of the plate, and ti is the thickness of the plate.
The size of the structural carrying capability can be characterized by the overall strain energy of the structure. When the loads are fixed, the smaller the strain energy of the structure, the smaller the structural flexibility, and the greater the structural stiffness is. The structural strain energy with the given loads and constraint boundary conditions satisfies the following equation:

where U is the structural strain energy, σ is the stress matrix, ε is the strain matrix, Ω is the structure volume, d is the structural displacement matrix generated by the load, and k is the structural stiffness matrix.
Topology optimization of the hydraulic press support plate structure requires an optimal compromise solution between the two objective functions of structural mass and carrying capability. Multi-objective optimization is usually performed for multiobjective problems to generate a series of Pareto solutions, and then a selective optimization is performed. In this study, the multi-objective topology optimization problem is converted into a single-objective problem. The norm method is often used for the transformation of multi-objective functions [35,36] in structural topology optimization. The distance function is defined as follows:

where 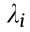 represents the weighting factor of the ith objective function,
represents the weighting factor of the ith objective function, 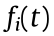 is the objective function value of the design variable,
is the objective function value of the design variable,  is the initial value of the objective function, and p is the penalty factor.
is the initial value of the objective function, and p is the penalty factor.
The topology optimization design of the hydraulic press support plate structure adopts the ground structure method. The plate thickness is the design variable, and the objectives are minimizing the strain energy and weight of the plate structure. For calculation convenience, the two targets are multiplied by the weight and combined into one target 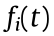 . There are different orders of magnitude between different objective functions in the topology optimization. If the actual value is taken as the optimization target directly, the objective function of a smaller order will recede, and that of a larger order will dominate. Therefore, a normalization process is required during the modeling of the multi-objective functions. A mixed-variables topology optimization model that considers both the cross-section and topological variables is adopted for this topology optimization problem. The design variables to be solved are the topological variables r = [ r1,r2, …,rn ]T and plate thickness variable t = [ t1,t2,… ,tn] T .
. There are different orders of magnitude between different objective functions in the topology optimization. If the actual value is taken as the optimization target directly, the objective function of a smaller order will recede, and that of a larger order will dominate. Therefore, a normalization process is required during the modeling of the multi-objective functions. A mixed-variables topology optimization model that considers both the cross-section and topological variables is adopted for this topology optimization problem. The design variables to be solved are the topological variables r = [ r1,r2, …,rn ]T and plate thickness variable t = [ t1,t2,… ,tn] T .


where W0 is the structural initial weight, E is the structural objective strain energy, E0 is the structural initial strain energy, 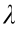 is the weighting factor, [σ] is the allowable stress constraint, [u] is the permissible maximum displacement, tw is the thickness of the plate that is not allowed to be deleted, tv is the thickness of the plate that can be deleted, Tw is the thickness set of the plate that is not allowed to be deleted, Tv is the thickness set of the plate that can be deleted, rw is the topological variable of the plate that cannot be deleted, and rv is the topological variable of the plate that can be deleted.
is the weighting factor, [σ] is the allowable stress constraint, [u] is the permissible maximum displacement, tw is the thickness of the plate that is not allowed to be deleted, tv is the thickness of the plate that can be deleted, Tw is the thickness set of the plate that is not allowed to be deleted, Tv is the thickness set of the plate that can be deleted, rw is the topological variable of the plate that cannot be deleted, and rv is the topological variable of the plate that can be deleted.
In the above topology optimization model (Eq. (4)), the constraints are divided into the stress and displacement constraints. The stress constraint limits the stress at the specified point of the structure to values not greater than the allowable stress of the material. The displacement constraint refers to the requirement that the displacement in the specified position of the structure is smaller than the specified allowable displacement. The multiobjective topology optimization of the structure obtains a series of feasible solutions. They are judged by the discriminant function to determine the optimal compromise solution, thus obtaining the final result. The discriminant function c is expressed as follows:

where  is the ideal feasible solution for the ith objective function. By calculating the discriminant function value corresponding to different weighting factors, a corresponding weighting factor, which is optimal when the discriminant function value is extremely small, is obtained. The topology optimization result under this weighting factor is the final optimization result.
is the ideal feasible solution for the ith objective function. By calculating the discriminant function value corresponding to different weighting factors, a corresponding weighting factor, which is optimal when the discriminant function value is extremely small, is obtained. The topology optimization result under this weighting factor is the final optimization result.
《3. Reliability analysis of the hydraulic press support plate structure》
3. Reliability analysis of the hydraulic press support plate structure
The parameters involved in the reliability analysis of the hydraulic press support plate structure were divided into deterministic and uncertainty parameters. Deterministic parameters, together with the optimization objective function and constraints, constitute a mathematical optimization model.
The uncertainty variables involved in the topology optimization include the material mechanics parameters, external load magnitude, and plate height. In this study, we use a probabilistic model to describe these variables and study their stochastic uncertainties. The uncertainty parameters are transformed into stochastic variables that conform to a certain probability distribution, such as normal and exponential distributions. Then, the probability distribution of the structural response is obtained. The mathematical model of the reliability topology optimization can be described as

where y is the vector of stochastic variables, considering E, the external load magnitude F, and the uncertainty of the plate height H, and  is the objective function.
is the objective function.  expresses the probability of structural failure,
expresses the probability of structural failure,  is the allowable failure probability, and
is the allowable failure probability, and  is the other constraint for the structure.
is the other constraint for the structure.
The reliability topology optimization aims to complete the optimal design of the structure, guaranteeing that the failure probability is less than the allowable failure probability. During the optimization calculation, the probability density distributions and accurate performance functions of the uncertain parameters need to be provided to accurately calculate the failure probability. Theoretically, structural reliability can be obtained through an integral calculation of the joint probability density function. However, in practice, the function is usually high dimensional, and the limit state function is implicit. In the general reliability design process, an approximation method is often used to make the limit state function explicit or to approximate the failure probability calculation by means of the local expansion method. The independent random input variables are transformed into standard normal random variables when using the first-order second-moment method to calculate the reliability index. The failure probability works in the standard normal space instead of the original space. The point closest to the origin on the limit state surface is defined as the most probable failure (MPP) point. Furthermore, the shortest distance from the origin on the limit state surface is the reliability index β. Thus, the failure probability is transformed into a reliability index constraint for the expression:

where  is the reliability index of the ith limit state of the structure and
is the reliability index of the ith limit state of the structure and 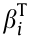 is the corresponding target reliability index.
is the corresponding target reliability index. 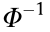 is the inverse function of the standard normal distribution to transfer the allowable failure probability
is the inverse function of the standard normal distribution to transfer the allowable failure probability  into
into  .
.

Traditional reliability optimization design with uncertainties includes a topology optimization iterative process and reliability analysis process. Both are nested within each other, which complicates the solution process. The decoupled method is an efficient and feasible method for solving reliability-based optimization problems with high dimensions, small failure probability, or complicated or implicit limit state functions. Solving the failure probability function is key in the decoupled method. The failure probability function is defined as a function that changes with the design variables, such that the original problem can be transformed into a conventional deterministic optimization problem. The transformed deterministic optimization problem can be solved using general optimization algorithms. In our problem, the reliability topology optimization process is divided into two parts after applying the decoupled method: the reliability analysis and deterministic topology optimization. The geometric meaning of the reliability index in the first-order reliability method is shown in Fig. 3. We can find the design point P* corresponding to the reliability index and sensitivity information of the function for the stochastic variable. Then, the uncertainty parameter is modified based on the sensitivity information. This makes the uncertainty parameters deterministic, enabling us to conduct deterministic topology design optimization based on obtained deterministic parameters.
《Fig. 3》

Fig. 3. Geometric meaning of first order reliability. μ1: the first normalized stochastic variable; μ2: the second normalized stochastic variable; μ1*: the first normalized stochastic variable of the most likely failure point; μ2*: the second normalized stochastic variable of the most likely failure point; P* : design point.
For a given failure case, combined with the geometric meaning of the reliability index, the reliability index β can be solved using the following optimization model for the stochastic variable [37]:

where μ is the normalized stochastic variable.
During the solution process, the sensitivity of the structural reliability index to the normal stochastic variable can be solved as
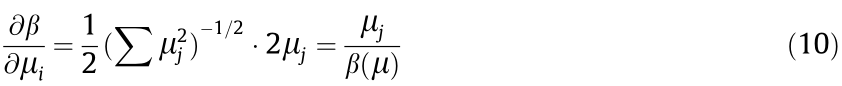
Solving the optimal solution obtained can be understood as finding the MPP μ* for a given failure situation. The stochastic parameters of the model are modified into deterministic parameters using μ*. The modification process is expressed as

where 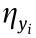 and
and 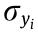 represent the mean and standard deviation of the uncertainty parameter yi, respectively. For calculating the sensitivities of the uncertain parameters in the above objective function, the finite difference method is used
represent the mean and standard deviation of the uncertainty parameter yi, respectively. For calculating the sensitivities of the uncertain parameters in the above objective function, the finite difference method is used

After modifying the uncertain parameters, the reliability topology optimization problem of the plate structure can be transformed into an equivalent deterministic topology optimization problem.
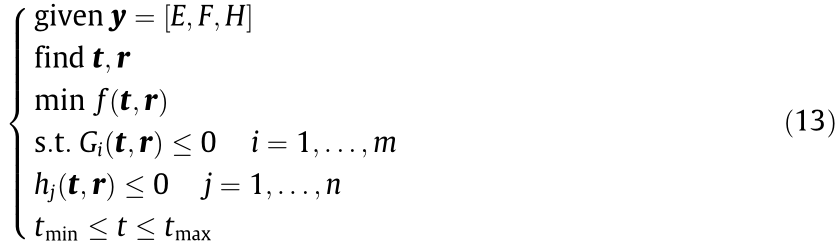
The reliability topology optimization calculation using the decoupled method ignores the influence of the performance function. However, it effectively improves the calculation efficiency and facilitates the optimization calculations in combination with the heuristic method.
《4. The process of the optimization solution》
4. The process of the optimization solution
The TLBO algorithm chosen in this study is a swarm intelligence algorithm with advantages in terms of convergence and efficiency. In contrast with most nature-inspired optimization algorithms, the TLBO algorithm has no optimum controlling parameters that influence the performance of algorithm. For TLBO, it is assumed that the behavior of nature is always optimum in its performance, which also reduces the complexity of the algorithm initialization. This algorithm has been thoroughly explored and developed through numerous studies. Rao et al. [38] proposed the TLBO algorithm to simulate teaching and learning processes. The TLBO algorithm and its improvement have been applied to various optimization scenarios [39,40], including discrete structural optimization. Tog˘an [41] used the TLBO algorithm for the design optimization of planar steel frames. Degertekin and Hayalioglu [42] and Camp and Farshchin [43] applied the TLBO algorithm to the design optimization of a plane truss and a space truss, respectively. Dede [44] optimized a truss structure using the TLBO algorithm using discrete design variables.
According to the reliability topology design optimization applied to a hydraulic press support plate structure, the optimization calculation based on a series of uncertainty parameters enables the structure to reflect the engineering practice more realistically. The reliability topology optimization flowchart is shown in Fig. 4.
《Fig. 4》

Fig. 4. Flowchart of the reliability topology optimization of a hydraulic press support plate structure.  : the value of the ith student before learning;
: the value of the ith student before learning;  : the values of the ith student after learning; TF: the learning factor; Xi, Xj: two different random students; Mg : the mean of the individual design variables; g: the number of iterations; r*: the random number.
: the values of the ith student after learning; TF: the learning factor; Xi, Xj: two different random students; Mg : the mean of the individual design variables; g: the number of iterations; r*: the random number.
After the reliability analysis of the hydraulic press support and its modification according to the uncertainty parameters, the topology optimization solution is obtained using the TLBO algorithm, which is divided into two phases: teaching and mutual learning.
《4.1. Population initialization》
4.1. Population initialization
The initial population of N-dimensional P columns is randomly generated, where N represents the number of students and P is the number of variables. The number of maximum iterations G and the initial conditions, together with the upper and lower limits of each variable, are specified. The population generation process is shown in Eq. (14), where the value is a random number between 0 and 1.

where  is the initial individual;
is the initial individual;  are the upper and lower limits of the variable, respectively; r* is the random number.
are the upper and lower limits of the variable, respectively; r* is the random number.
《4.2. Teaching phase》
4.2. Teaching phase
In this phase, the adaptive value of each individual in the initial population is calculated. Then, the optimal individual is selected as the ‘‘teacher” to teach other individuals, namely, ‘‘students.” When the number of iterations is g,  represents the ‘‘teacher” individual in the current population and Mg is the mean of the individual design variables. The ‘‘student” learns and improves according to Eq. (15):
represents the ‘‘teacher” individual in the current population and Mg is the mean of the individual design variables. The ‘‘student” learns and improves according to Eq. (15):
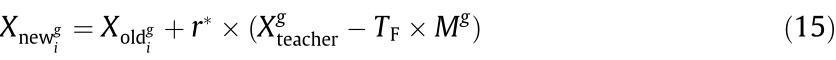
where  represent the values of the ith student before and after learning, respectively, and TF represents the learning factor, which is generally randomly selected in 1 or 2.
represent the values of the ith student before and after learning, respectively, and TF represents the learning factor, which is generally randomly selected in 1 or 2.
《4.3. Mutual learning phase》
4.3. Mutual learning phase
Each student improves their individual adaptive value through a mutual study in this phase. After the teaching phase, for a random student Xi, another student Xh (h ≠ i) is chosen to analyze the gap between the two students and adjust them simultaneously.
As the topology variable is a discrete value in the topology optimization of the plate structure, it is regarded as a continuous variable between [0, 1] during iterative learning. The topology variable is rounded when calculating the objective function value and the constraints, and in the final calculation when the results are expressed. This processing mode ensures that the topology variable remains random during the learning evolution process.
The standard TLBO algorithm cannot process the constraint problems involved in engineering applications. The penalty function is introduced to transform the problem with constraints into a problem without constraints. The general form of the penalty function is

where 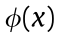 is the synthetic objective function added to the penalty term and p(x) is the penalty term, which is expressed as
is the synthetic objective function added to the penalty term and p(x) is the penalty term, which is expressed as
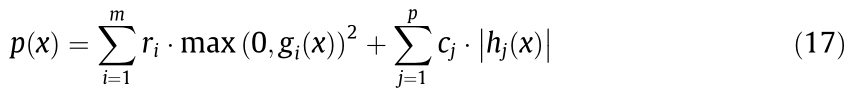
where ri and cj are penalty factors, and gi(x) and hj(x) are the inequality and equality constraints, respectively.
In the calculation process of the standard TLBO algorithm, the change in the learning factor TF is crucial, the value of which can affect the rate and accuracy of the iterative search. Generally, the value of the teaching factor is randomly selected as 1 or 2 by the system. In the calculation process of the optimization iteration, if TF is small, the convergence rate of the optimization process will slow down, and the search will be more refined. If the value is large, the convergence rate will be faster, but the algorithm will likely be premature. The value of TF was discussed and improved by Rao et al. [45], and the TLBO algorithm was also optimized. Niknam et al. [46] associated the value of the teaching factor with the current students’ average grades and the teacher’s level. TF is represented as the ratio of the students’ grades (Mi) to the teacher’s level (Ti) at the ith iteration: TF = Mi/Ti. In this study, an adaptive teaching factor calculation method [47] is adopted, expressed as

where Mopt,i is the average grade of each student after the ith iteration through teaching and mutual learning optimization.  = 1; when
= 1; when  is 0, TF equals 1. This value of the teaching factor makes the convergence rate faster in the initial search stage, whereas a more detailed search is utilized after several iterations up to a certain number of times.
is 0, TF equals 1. This value of the teaching factor makes the convergence rate faster in the initial search stage, whereas a more detailed search is utilized after several iterations up to a certain number of times.
Griewank and Rastrigrin numerical functions were selected to compare the original TLBO and the improved algorithms, verifying the effectiveness of the improvement. The two functions are both typically nonlinear multimodal functions with many local minima. It is difficult to find their global minima through optimization algorithms. The function dimension was set as 30, the algorithm population size as 10, the maximum number of iterations as 100, the maximum value of the teaching factor as 2, and the minimum value as 1.
Both the original TLBO and the improved TLBO algorithms can converge to a global optimal value after a certain number of iterations. However, the improved TLBO algorithm has obvious advantages in terms of convergence speed compared to the original algorithm. The original TLBO algorithm did not converge to the global optimal value until more than 90 generations, whereas the improved TLBO algorithm converged in less than 20 generations. The test results prove that the improved algorithm jumps out of the local optimum more easily. The algorithm efficiency is greatly improved as well when calculating the topology optimization of a high-dimensional complex model.
《5. Example analysis》
5. Example analysis
The hydraulic press support is a box-shaped plate structure. It is mainly made of polygonal plates created through welding or casting. The interior is staggered with plates to form an independent space. The upper part is supported by a load-bearing plate. The plate arrangement of the hydraulic press support is different owing to the different manufacturing processes. The ground structure needs to be constructed differently for different process forms to reflect the plate arrangement and process characteristics in the topology optimization. There are two typical forms of the arrangement shown in Fig. 5: neat grids and staggered grids. In the following, we introduce topology optimizations for the neat grid and the staggered grid layouts. Both optimization objectives consist of the total mass and load stiffness of the plate structure, whereas the local maximum displacement is set as a constraint to meet the reliability requirements.
《Fig. 5》
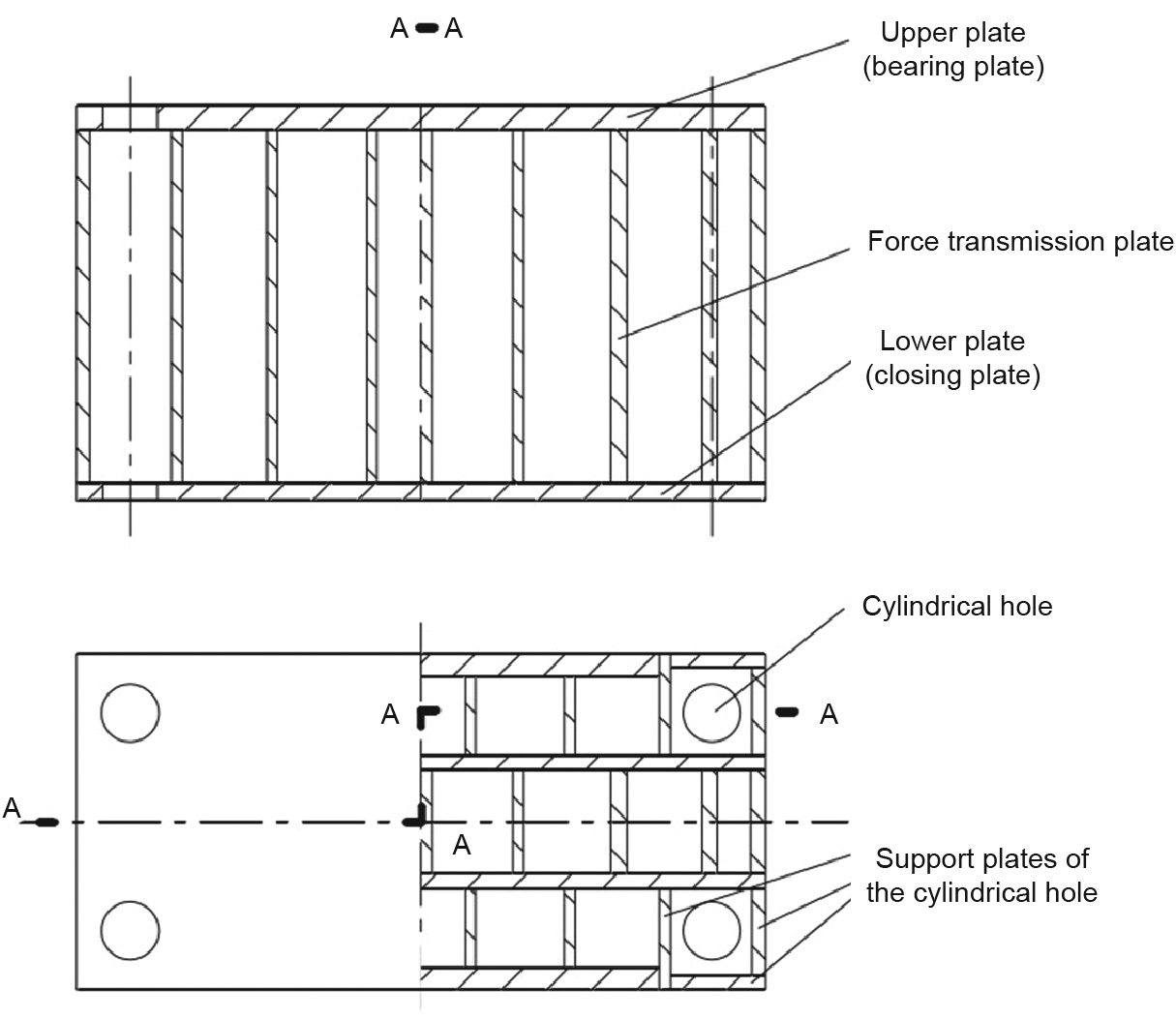
Fig. 5. Welded plate structure.
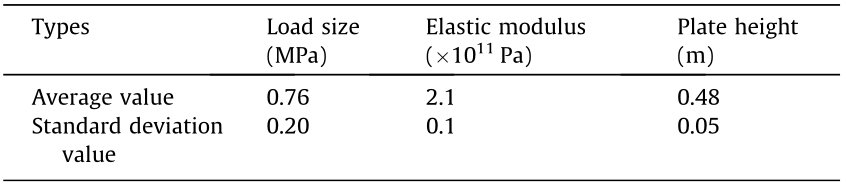
The structural design parameters are listed in Table 1. The target performance is defined by the overall strain energy of the structure. The structure mass was constrained to 80% of the original mass of the structure. The number of iterations was set to 100. The upper limit thickness of each plate was set to 5 cm, and the maximum displacement of the bearing plate was set to 2.5 mm in the z direction. The boundary condition adopted the complete constraint around the cylindrical hole of the bottom plate, and loads were applied in a 1.8 m × 1.2 m rectangular area at the center of the upper plate, where the displacement constraint was used. The load, material elastic modulus, and plate height were all set as normal stochastic variables. The structural uncertainty parameters are presented in Table 2. After setting the parameters, the decoupled method was used to calculate and correct the sensitivity of the stochastic variables. Then, the corrected stochastic variables were substituted into the mathematical topology optimization model for the calculation.
《Table 1》
Table 1 The values of structural design parameters.

《Table 2》
Table 2 Values of uncertain parameters before modification.
The support plates of the cylindrical hole at the four corners of the base are set as non-removable plates because of their functionality, whereas the other support plates can be added or deleted. The topology optimization target reliability 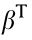 was set to 3, and the ideal weighting factor
was set to 3, and the ideal weighting factor  was selected as 0.8 according to the optimization iteration results and the discriminant function (Eq. (5)). The layout of the carrier plate is symmetrical so that only the lower left quarter is required for modeling analysis, whereas the rest is calculated using a symmetric method. In the example, the materials in each part are the same; thus, only the structural volume is calculated as the objective function. The optimized topology variables and plate thickness variables of each plate are listed in Tables 3 and 4, respectively. The final topology optimization results are listed in Table 5. The neat grid and staggered grid structures, together with their numbers, are shown in Figs. 6 and 7, respectively. The topology optimization iterative process and final optimization results are shown in Figs. 8–11.
was selected as 0.8 according to the optimization iteration results and the discriminant function (Eq. (5)). The layout of the carrier plate is symmetrical so that only the lower left quarter is required for modeling analysis, whereas the rest is calculated using a symmetric method. In the example, the materials in each part are the same; thus, only the structural volume is calculated as the objective function. The optimized topology variables and plate thickness variables of each plate are listed in Tables 3 and 4, respectively. The final topology optimization results are listed in Table 5. The neat grid and staggered grid structures, together with their numbers, are shown in Figs. 6 and 7, respectively. The topology optimization iterative process and final optimization results are shown in Figs. 8–11.
《Table 3》
Table 3 Topology and size variables of the optimal neat grid plate structure.

《Table 4》
Table 4 Topology and size variables of the optimal staggered grid plate structure.
《Table 5》
Table 5 Comparison of the topology optimization results.

《Fig. 6》

Fig. 6. Neat grid ground structure.
《Fig. 7》

Fig. 7. Staggered grid ground structure.
《Fig. 8》
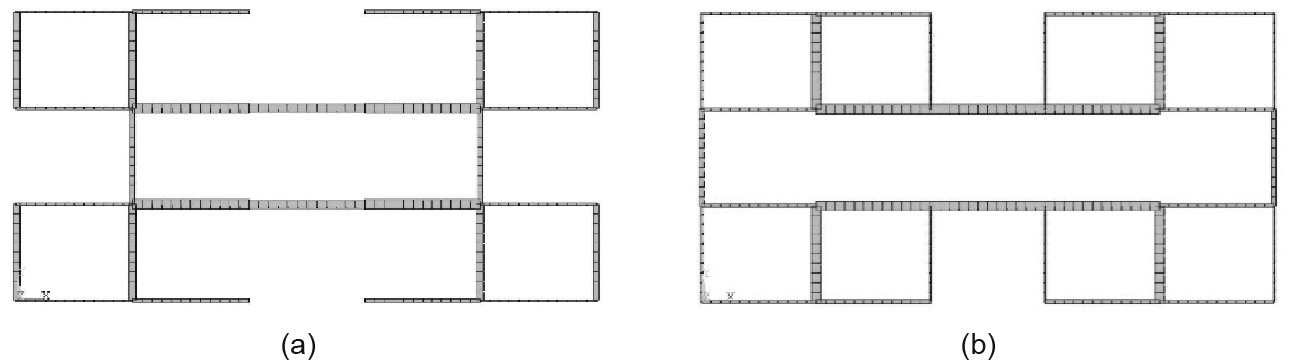
Fig. 8. Topology optimization of the neat grid ground structure. (a) Deterministic topology optimization results; (b) reliability topology optimization results (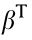 = 3).
= 3).
《Fig. 9》
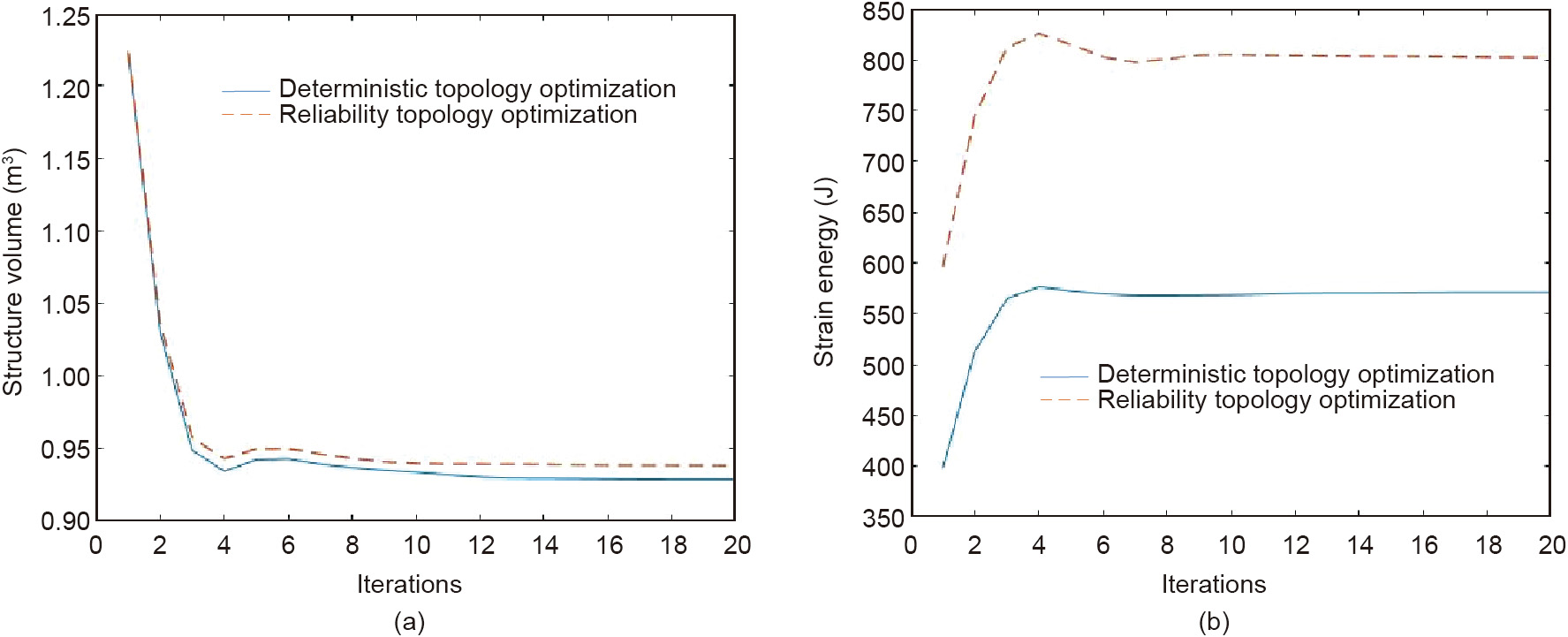
Fig. 9. Convergence process of the objective function of the neat grid ground structure. (a) Volume convergence process; (b) strain energy convergence process.
《Fig. 10》

Fig. 10. Topology optimization of the staggered grid ground structure. (a) Deterministic topology optimization results; (b) reliability topology optimization results (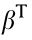 = 3).
= 3).
《Fig. 11》

Fig. 11. Convergence process of the objective function of the misaligned square structure. (a) Volume convergence process; (b) strain energy convergence process.
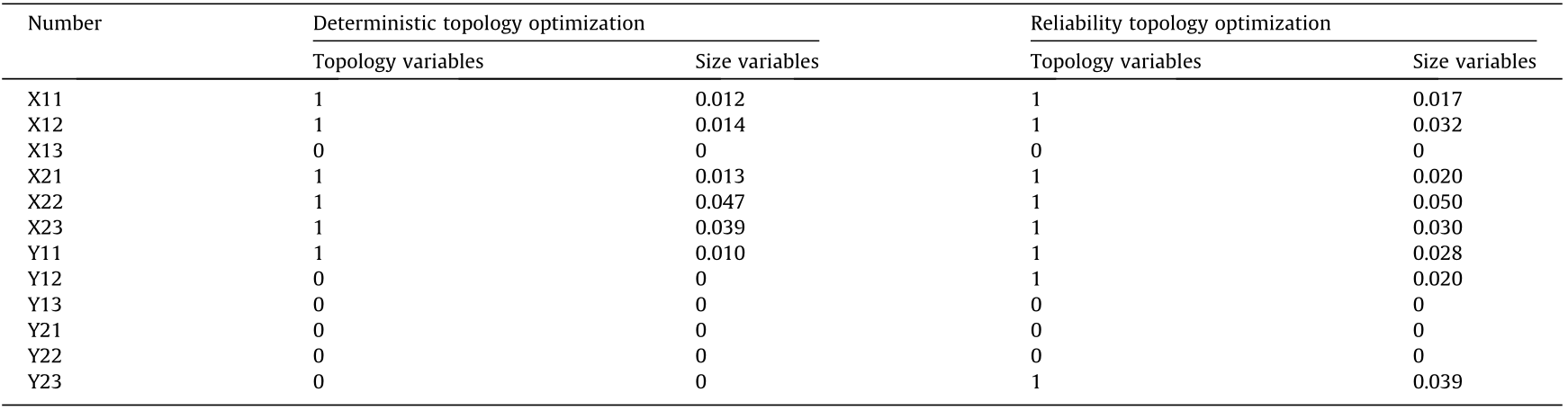
The topology configuration and plate element distribution after the optimizations of the neat grid and the staggered grid structures are shown in Figs. 8 and 10, respectively. Compared to the topology optimization results of the two ground structures, those acquired through reliability optimization have more retention plate elements than those acquired through deterministic optimization. Tables 3 and 4 show the quantitative data of the topology and plate thickness variables obtained through reliability and deterministic topology optimizations. In the neat grid structure, the plate thickness of plates X23 and Y12 near the center of the base was significantly increased. In addition, the topology variables of plates Y13 and Y21 became equal to 1 after reliability topology optimization. Similarly, the plate thickness variable was also significantly increased under the staggered grid structure. The topology variables of plates Y12 and Y23 near the center of the structure became equal to 1 after reliability topology optimization. The overall material quantity of the structure was increased, and the structural reliability was enhanced.
The iterative changes of the volume and strain energy objective functions are shown in Figs. 9 and 11, respectively, based on different ground structures. For the volume objective function in both ground structures, the final convergence value of the reliability topology optimization was greater than that of the deterministic topology optimization. This result is consistent with the intuitive results presented in Figs. 8 and 10. For the strain energy objective function, a higher strain energy results in a smaller support stiffness. The structural strain energy calculated through the reliability topology optimization was higher than that of the deterministic topology optimization. This indicates that after the stochastic parameters were modified, the structure satisfied the optimization constraints with a smaller support stiffness. As a result, the structure gained a stronger anti-failure capability and higher reliability.
Table 5 presents the deterministic and reliability topology optimization results for the two ground structures. It is seen that the optimization results satisfy the displacement constraint of 0.5 mm. Nevertheless, the results obtained using the two different ground structures were slightly different. The reliability topology optimization of the neat grid structure increased less in terms of the weight ratio, only increasing from 0.76 to 0.77. Furthermore, the weight ratio increased from 0.71 to 0.78 in the staggered grid structure. In both cases, the ratio of the overall strain energy of the final optimization result to that of the initial structure was significantly reduced using the reliability topology optimization process. The ratio of the strain energy of the neat grid to the original strain energy was 1.35, and the ratio of the strain energy of the dislocation grid to the original strain energy was 1.32. The reliability topology optimization lowers the structural support stiffness when the structure is lightweight. As a result, the structure can be constructed to satisfy a predetermined reliability index.
Compared to the deterministic topology optimization, the results obtained using the reliability topology optimization are more conservative, the weight is larger, the strain energy is smaller, and the overall stiffness of the structure is larger under uncertain conditions. However, compared to the unoptimized structure, the weights obtained using deterministic topology optimization as well as those obtained using reliability topology optimization decreased, while the strain energy increased. At the same time, the structure meets the reliability requirements and has a smaller risk of failure based on reliability topology optimization under uncertain conditions. Based on the numerical example, it can be concluded that the reliability topology optimization is effective in balancing the structural performance and environmental protection.
《6. Conclusions》
6. Conclusions
A lightweight design of a hydraulic press structure is carried out to save resources based on reliability to guarantee high performance. We studied the discrete topology optimization method with numerous uncertainties with the aim of reducing the mass of the hydraulic press support. First, the ground structure method was applied to divide the support of the hydraulic press into a plate structure, simultaneously changing the number of plate units and optimizing their sizes. Second, the uncertainties of the loads, size parameters, and material parameters were transformed into stochastic variables through a probability distribution. The failure function of reliability and uncertainties of the parameters were simplified based on the reliability index. The decoupled method divided the two-level nesting of the reliability calculation and topology optimization processes into two independent parts. Third, the TLBO algorithm was adapted to solve the decoupled model, offering few parameters, simple results, and a fast solution. We improved it by adding an adaptive teaching factor to make convergence faster in the initial stage while enabling finer searches in later stages. The design optimization of an actual hydraulic press was conducted using the proposed method to determine the optimal design scheme with respect to the layout and size. In this design, the materials of the support structure were fully used in an optimum position to achieve an overall lightweight structure, ensuring a balance in the structural design between economy and safety.
However, there are some limitations to this study. In some cases, the uncertain parameters can only be determined by a simple range, which the probabilistic model in this study fails to deal with. Moreover, the decoupled method neglects the impact of the performance functions of uncertain parameters to improve the calculation efficiency. The topology optimization based on reliability only reduces the energy and material costs to a small extent. In other words, it mainly enhances the utilization of each material unit. Future studies need to focus on these problems to achieve more suitable methods, propose a model to deal with uncertainties expressed in different forms, and try to continuously improve model accuracy in describing uncertainties. Future studies may investigate and apply an algorithm that is more efficient than a decoupled method to solve the reliability topology optimization problem. They may also combine the topology optimization with other optimization methods to achieve greater weight reduction and resource savings in hydraulic presses.
《Acknowledgments》
Acknowledgments
This work was supported by the National Natural Science Foundation of China (51935009 and 52105281).
《Compliance with ethics guidelines》
Compliance with ethics guidelines
Zhaoxi Hong, Xiangyu Jiang, Yixiong Feng, Qinyu Tian, and Jianrong Tan declare that they have no conflict of interest or financial conflicts to disclose.














 京公网安备 11010502051620号
京公网安备 11010502051620号




