一种改进BP算法在机械手逆运动学中的应用

摘要

通过对传统BP算法的分析，提出了一种改进激励函数的学习方法，并且在神经网络的每一层采用不同的学习速率，以提高训练速度；采用所提出的改进BP算法，训练多层前向神经网络，建立机械手逆运动学模型，仿真结果表明了该算法的有效性；与传统BP算法相比，大大提高了机械手逆运动学的精度。

正文

《1 引言》

1 引言

BP神经网络是目前研究最多、应用最广泛的一种多层前馈神经网络。虽然在理论上已经证明, 只要隐节点数足够多, 隐层采用Sigmoid激励函数的三层前馈神经网络, 可以以任意精度逼近任何连续映射, 然而基于误差梯度下降的标准BP算法, 存在着收敛速度慢、易陷入局部极小的问题。为此, 各国学者从BP网络的不同角度进行了改进, 如自适应调整学习速率, 采用牛顿法和共轭梯度法代替最速下降法^[1], 改进误差函数^[2], 或者将混沌优化法^[3]、遗传算法^[4]和模拟退火算法^[5]引入BP算法等方面。这些算法对提高BP算法收敛和克服局部极小均有进步意义, 但也有一定的局限性, 通常改进效果不是很明显, 就是在改进的同时又产生了另外的弊端。如变步长法可以避免震荡, 但网络的收敛速度将变慢;牛顿法与共轭梯度法虽可以加速收敛, 但计算过程非常复杂。

笔者在分析标准BP算法原理的基础上, 借鉴文献[6]的思想并加以改进, 发展了一种简单有效的学习方法, 并将其应用于机械手控制的逆运动学问题中。计算机仿真表明, 该方法能大大提高神经网络的收敛速度和逼近精度。

《2 机械手逆运动学问题》

2 机械手逆运动学问题

机械手运动学描述了机械手关节与组成机械手的各刚体之间的运动关系, 其运动学逆解 (inverse kinematics) 问题就是给定工具坐标系所期望的位形, 找出得到该位形的关节转角。通常, 机械手的期望轨迹都是在笛卡儿坐标中描述的。

对于一个已知的具有n个自由度的机械手, 在某一时刻t, 关节变量状态向量θ (t) =[θ₁ (t) , θ₂ (t) , …, θ_n (t) ]^T∈Rⁿ, 与机械手的位置向量x (t) =[x₁ (t) , x₂ (t) , …, x_m (t) ]^T∈R^m之间的关系可以由如下运动学方程描述:

$x = F (θ) (1)$ $x = F (θ) (1)$

式中F为机械手前向运动学函数。一般情况下, 它是一个非线性超越方程, 无法通过反解式 (1) 求其解析解, 通常都是求其数值解。传统的反解策略是建立机械手位置状态向量与关节状态向量的微分运动, 从而求解某机械手的运动向量所必须的关节速度。

对式 (1) 两边求导, 得

$\dot{x} = J \dot{θ} (2)$ $\dot{x} = J \dot{θ} (2)$

式中 $\dot{x} = d x / d t ‚ \dot{θ} = d θ / d t ‚ J = \partial F / \partial θ \in R_{m \times n}$ $\dot{x} = d x / d t ‚ \dot{θ} = d θ / d t ‚ J = \partial F / \partial θ \in R_{m \times n}$ , 其中J称为机械手运动学方程的雅可比阵。在已知 $\dot{x}$ $\dot{x}$ 的情况下, 相应关节状态向量的速度为

$\dot{θ} = J^{+} \dot{x} (3)$ $\dot{θ} = J^{+} \dot{x} (3)$

式中J⁺=J^T (JJ^T) ^-1∈R_m×n, 称为雅可比阵的伪逆, 式 (3) 给出的解常称为关节速度的伪逆解。可见式 (3) 的计算需要有效的雅可比矩阵求逆算法, 计算过程非常复杂。

《3 神经网络算法》

3 神经网络算法

由于神经网络具有高度非线性的映射能力, 一个三层前向神经网络就可以逼近任意的非线性函数, 所以神经网络被广泛应用于机器人控制领域研究^[4,5,7]。

《3.1标准BP算法》

3.1标准BP算法

传统的多层前向神经网络的权系数都是采用BP算法来学习。这种学习算法由正向传播和误差反向传播两个过程组成。在正向传播过程中, 输入模式从输入层经隐层单元逐层处理和传播, 最后到输出层。同时, 将希望的输出和实际输出之间的二次误差, 沿原来的传递通路反向传播到输入层, 并以此调整各层神经元的权值系数, 最终使得误差信号最小。

设一个三层BP网络的输入层、隐含层、输出层节点数分别为M, Q, L, 各层节点依次用i, j, k表示。输入节点与隐节点间的网络权值为W_ij, 隐节点与输出节点间的网络权值为W_jk。

设有N个训练样本, 对应第p个样本输入输出模式x_p和d_pk进行如下训练。对样本p完成加权系数的调整后, 再送入另一样本模式对进行类似学习, 直到完成N个样本的训练学习为止。

根据一阶梯度法进行推导, 得到下面的权系数修正公式:

1) 隐层至输出层权系数的调整公式

对于输出节点k:

$Δ_{p} W_{j k} = η (d_{p k} - Ο_{p k}) f ̌ (n e t_{p k}) Ο_{p j} = η δ_{p k} Ο_{p j} (4)$ $Δ_{p} W_{j k} = η (d_{p k} - Ο_{p k}) f ̌ (n e t_{p k}) Ο_{p j} = η δ_{p k} Ο_{p j} (4)$

式中δ_pk= (d_pk-O_pk) f´ (net_pk) , η为学习速率, 且η>0, f´ (net_pk) 为激励函数的导数, net_pk表示第k个节点的输入 (下同) 。

2) 输入层至隐层权系数的调整公式

对于隐含节点j:

$Δ_{p} W_{i j} = η f ̌ (n e t_{p j}) (\sum_{k = 1}^{L} δ_{p k} W_{j k}) Ο_{p i} (5)$ $Δ_{p} W_{i j} = η f ̌ (n e t_{p j}) (\sum_{k = 1}^{L} δ_{p k} W_{j k}) Ο_{p i} (5)$

从上面的公式可以看出, 网络的拓扑结构和训练数据确定之后, 总误差函数E的性质特征就完全由激励函数决定了^[8]。由于激励函数的导数在学习过程中被大量地使用, 因此对整个网络的学习过程影响非常大。

由于S型的激励函数都存在饱和区, 从而导致麻痹现象的产生。当神经元的输出落入激励函数饱和区时, 激励函数的导数数值很小, 因此每次学习周期只能对权值做较小修正, 输出单元会在一段时间工作在平坦区中, 使网络的均方根误差保持不变或变化很小。此时, 相当于整个调节过程几乎停顿下来, 从而产生了所谓的麻痹现象, 减慢了网络的收敛速度。

为了避免麻痹现象的产生, 文献[6]提出了一种在学习过程中动态调整激励函数参数的BP算法。当神经元的输出落入激励函数饱和区时, 使激励函数导函数值可以随误差的变化而做相应的调整, 以加快网络的收敛速度, 有效地避免麻痹现象的产生。但是, 可调参数的学习, 无形中增加了每次训练学习的时间, 增加了方法的复杂性。因此, 笔者采取下面的方法, 可避免参数的学习, 以降低问题的复杂性。

《3.2激励函数》

3.2激励函数

首先对几个常用的激励函数进行分析:

1) logsig对数S型 (sigmoid) 传递函数可以将神经元的输入范围 (-∞, +∞) 映射到 (0, 1) 的区间上, 它是可微函数, 其表达式为f (x) =1/ (1+e^-x) 。

2) tansig双曲正切S型 (sigmoid) 传递函数可以将神经元的输入范围 (-∞, +∞) 映射到 (-1, +1) 的区间上, 它是可微函数, 其表达式为f (x) = (1-e^-x) / (1+e^-x) 。

3) purelin线性函数这也是可微函数, 其输出可以是任意值, 表达式为f (x) =x。

可以看出, 对于一个三层BP网络而言, 如果最后一层是sigmoid型神经元, 会使网络的输出限制在一个较小的范围内;而purelin型神经元, 则使得网络的输出可以是任意值。所以笔者选择purelin函数作为输出层的激励函数。

在标准BP算法中, 隐层神经元的激励函数通常取为logsig函数。一般认为, tansig函数比logsig函数的输出范围大, 且含正负区间, 所以很多学者把tansig函数作为隐层神经元的激励函数。笔者研究发现, 采用tansig函数并不一定总是比logsig函数效果好。采用何种激励函数, 需要视具体情况而定。它与网络的期望输出数据的特点密切相关, 当期望输出数据都为正数时, 采用logsig函数更具优势。因为正的隐层神经元输出值, 可以使网络能更快地接近期望输出, 仿真结果也证明了这一点。

《3.3激励函数的改进》

3.3激励函数的改进

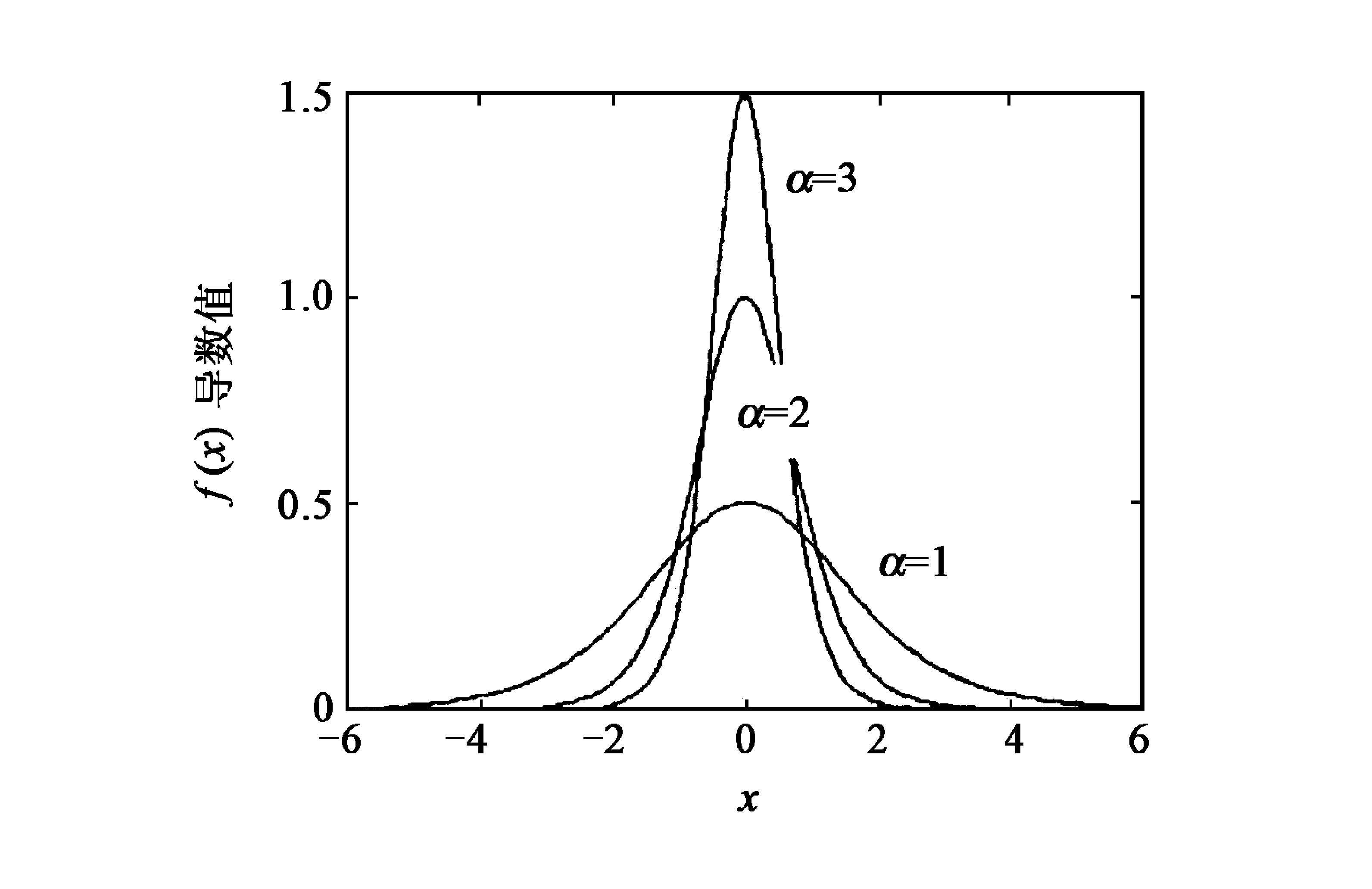
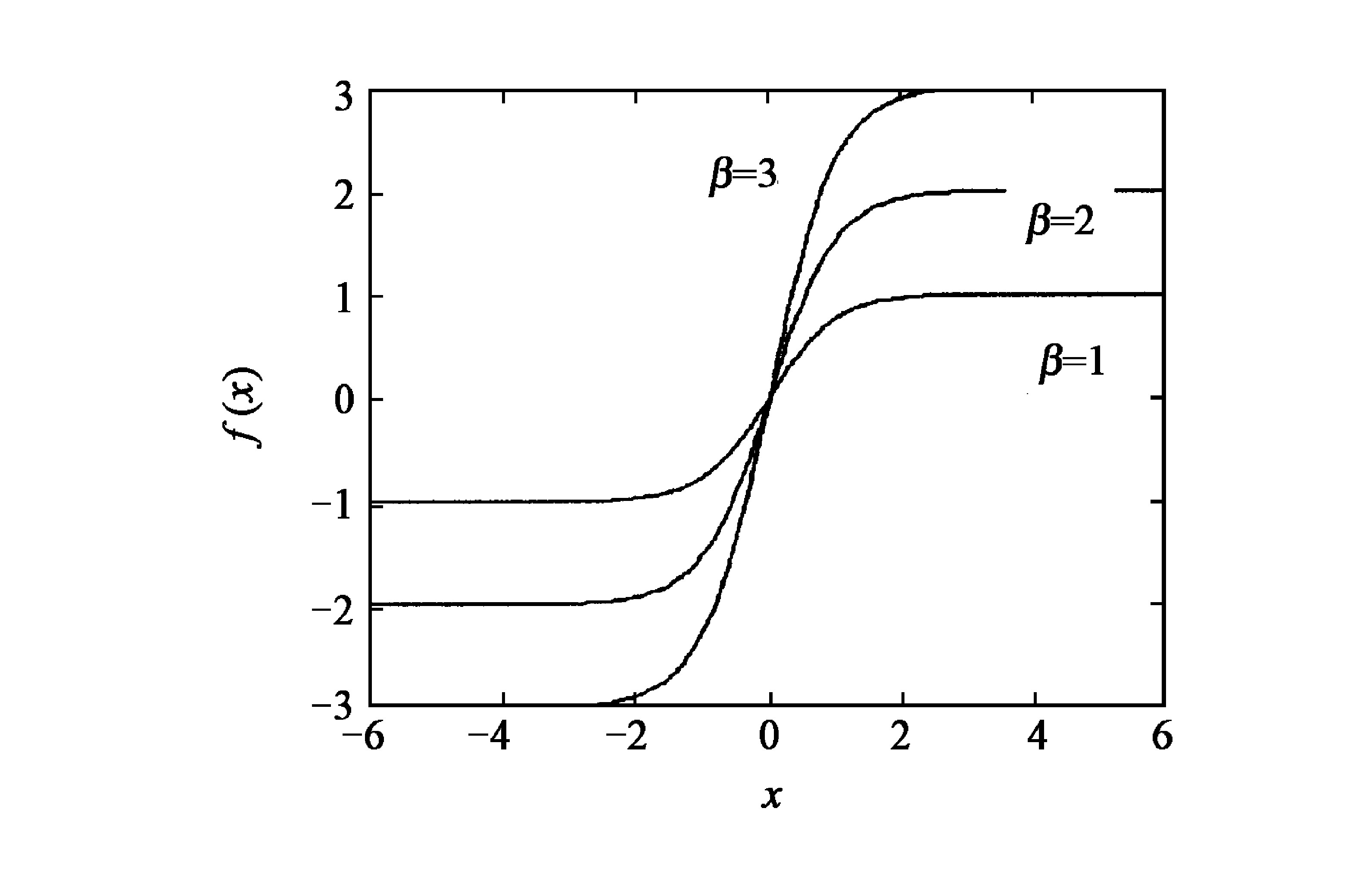
以tansig函数为例 (logsig函数也类似) , 改进后的激励函数为f (x, α, β) =β (1-e^-αx) / (1+e^-αx) , 其中α, β为激励函数的可调因子。它们对激励函数及其导数的影响如图1至图4所示, 随着α值的减小, 激励函数的有效范围 (这里是指脱离饱和区影响的程度) 扩大, 但是激励函数的斜率降低了, 即激励函数的导数减小了;而随着β值的变化, 改变了激励函数及其导数的值域。

《图1》

图1 参数α对激励函数的影响

Fig.1 Effects of parameter α on active function

《图2》

图2 参数α对激励函数导数的影响

Fig.2 Effects of parameter α on derivative of active function

《图3》

图3 参数β对激励函数的影响

Fig.3 Effects of parameter β on active function

《图4》

图4 参数β对激励函数导数的影响

Fig.4 Effects of parameter β on derivative of active function

可见, 应该在保证神经元的输出避免落入激励函数饱和区的前提下, 选择较大的调节因子α, 以增加激励函数及其导数的陡度, 提高网络的学习速度。同时, 选择较大的调节因子β也能够增加激励函数及其导数的陡度, 并能弥补因α较大导致激励函数易陷入饱和区的缺陷。但是, 这两个调节因子又不能太大, 否则会引起学习过程震荡, 导致过程不收敛。所以调节因子α和β需要选择适当, 其大小由网络的初始权值和训练数据决定。

《3.4学习速率的改进》

3.4学习速率的改进

在标准BP算法中, 算法对学习速率的设置非常敏感。在网络的学习初始阶段, 选择较大的学习速率可使收敛速度明显加快, 但在接近误差极小点时, 过大的学习速率将导致权值调整幅度过大而产生震荡或不收敛;反之, 小的学习速率虽不会产生震荡, 但是越小, 收敛就越慢, 且可能更易陷入较“深”的局部极小点。

真正的梯度下降是沿着梯度确定的方向以无穷小步长进行的。很明显, 这是不切实际的。但是, 选择小的学习速率η会使网络收敛到较高的精度。然而, 这样又会导致网络的学习速度变得很慢。由于笔者在改进的激励函数中引入调节因子β, 增加了梯度值, 所以可以选择较小的学习速率, 而不致于使网络的学习速度变得很慢。

文献[9]指出, 在标准BP算法中, 输出层与隐层之间的权值调节量要远大于隐层与输入层在学习过程中的权值调节量。这样, 它们对网络训练的贡献有超过一个数量级的明显差别。当隐层与输出层之间权值调节量处于合适值时, 输入层与隐层之间的权值调节量则太小, 不能有效地参与学习过程;当输入层与隐层之间的权值调节量处于合适值时, 隐层与输出层之间权值调节量太大, 易产生过调。因此, 要加快网络的收敛速度, 应该使二者协调一致, 达到对网络训练相同的贡献。为此, 笔者对每层神经元采用不同的学习速率, 使不同层之间的权值处在一个数量级。

《4 仿真实例》

4 仿真实例

为了验证本文方法的有效性, 同时为方便对比研究, 笔者采用文献[4]中的模型参数和训练数据, 对一个两杆平面机械手进行了仿真实验, 如图5所示。

《图5》

图5 两连杆平面机械手模型

Fig.5 The model of two-ink planar manipulator

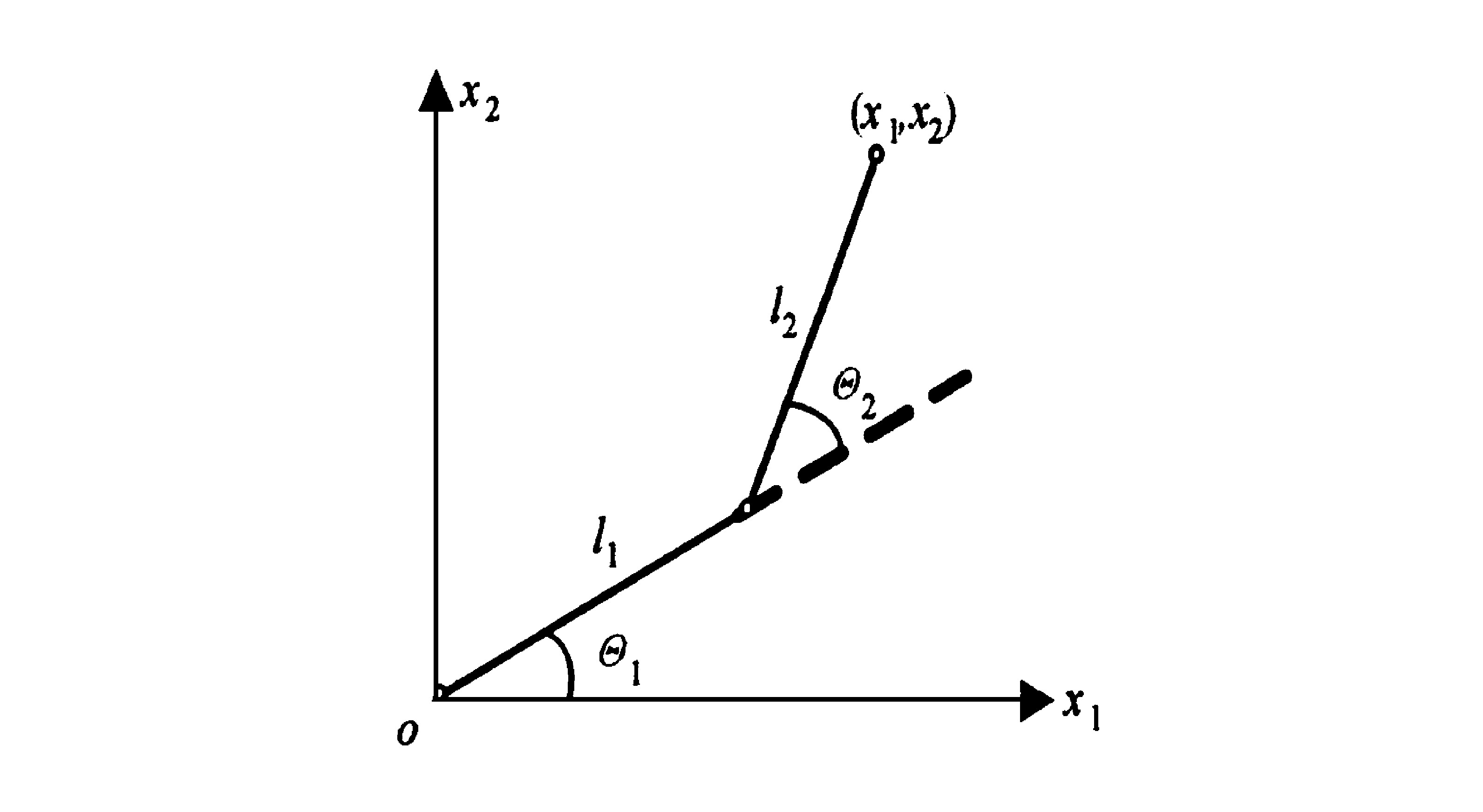
忽略连杆的质量, 机械手的前向运动学方程为

$\begin{array}{l} x_{1} = l_{1} \cos θ_{1} + l_{2} \cos (θ_{1} + θ_{2}) \\ x_{2} = l_{1} \sin θ_{1} + l_{2} \sin (θ_{1} + θ_{2}) \end{array}$ $\begin{array}{l} x_{1} = l_{1} \cos θ_{1} + l_{2} \cos (θ_{1} + θ_{2}) \\ x_{2} = l_{1} \sin θ_{1} + l_{2} \sin (θ_{1} + θ_{2}) \end{array}$

式中l₁, l₂为连杆长度, 取l₁=l₂=1.0 m;x₁, x₂为机械手终端位置;θ₁, θ₂为机械手连杆转角。

由两杆平面机械手的期望运动轨迹, 得到神经网络的训练数据如表1所示。

表1 神经网络的训练数据

Table 1 The learning data of neural network

《表1》

sample	x₁/m	x₂/m	θ₁/rad	θ₂/rad
1 2 3 4 5 6 7 8 9	1.0 0.9 0.8 0.7 0.6 0.5 0.5 0.6 0.7	0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95	-0.460 7 -0.411 4 -0.347 0 -0.267 6 -0.173 8 -0.067 4 -0.016 1 -0.016 6 -0.003 9	1.927 0 1.998 7 2.058 7 2.106 0 2.139 7 2.159 2 2.110 3 1.998 7 1.879 4

采用网络结构均为N_{2, 10, 1}的两个不同的三层前向神经网络, 来建立两杆平面机械手模型, 对两个关节角分别进行学习。由于机械手模型的两个关节角期望输出的值域不同, 所以隐层选用不同的激励函数, 而输出层都选用线性purelin函数。关节1的数据中含有负值, 故隐层节点选择改进的tansig型激励函数;而关节2的数据均为正值, 故隐层节点选用改进的logsig型激励函数。

采用笔者提出的改进BP算法来训练网络, 关节1模型的激励函数为f (x, α, β) =β (1-e^-αx) / (1+e^-αx) , 其中α=3, β=2, 隐层和输出层的学习率分别为0.06和0.003;关节2模型的激励函数为f (x, α, β) =β/ (1+e^-αx) , 其中α=1.5, β=3, 隐层和输出层的学习率分别为0.07和0.01;以上参数均经过优化。经过1 500代的学习, 得到了较理想的结果。

图6, 图7分别为两个关节角度的仿真结果及与期望结果的比较。关节角θ₁, θ₂的均方差分别为2.36×10^-4和2.82×10^-4, 与文献[4]中采用遗传算法所得的结果2.29×10^-4和3.56×10^-4相近, 而且所获得的关节2的精度更高。与标准BP算法经过3 000次迭代得到1.1×10^-2和0.7×10^-2的结果相比, 笔者的改进算法大大提高了求解精度。

《图6》

图6 关节1的期望输出与仿真输出曲线

Fig.6 The output curve of expectation and simulation of joint θ₁

《图7》

图7 关节2的期望输出与仿真输出曲线

Fig.7 The output curve of expectation and simulation of joint θ₂

《5 结语》

5 结语

笔者通过分析激励函数在标准BP算法中的作用, 对激励函数加以改进, 引入调节因子, 扩大激励函数的有效作用范围, 远离饱和区;并且适当改变激励函数的值域, 增加其陡度, 以利于改善算法的收敛性。通过合理选择激励函数的类型, 以及每层采用不同的学习速率, 克服了标准BP算法收敛速度慢的缺点。改进的方法中所含参数少, 保持了传统BP算法的简洁性, 只是在参数的确定上需要依靠经验进行优化。仿真结果表明, 此方法能够有效地求解机械手逆运动学问题, 而且求解精度较高。同时, BP网络及其算法还有很多需要深入研究的地方。

展示更多