平坦快衰落条件下天线数较多时空时格码的设计

摘要

空时格码技术是近年来无线通信领域的一个研究热点，空时格码的设计准则问题一直是该技术的一个难点。在平坦快衰落条件下且天线数目较多时，基于最小平方欧式距离最大化的空时格码设计准则虽然优于经典的距离－积准则，但仍不完善。从平方距离分布与平方距离和方－方和比分布的角度对此进行了改进，得到改进的准则以及性能为目前最优的新码。还对快慢2种衰落条件下码性能差异的原因给出了新的解释，并将改进的码设计准则应用于智贪码的设计。

正文

《1 引言》

1 引言

近年来发展起来的空时格码技术 (STTC) 由于能同时带来分集和编码增益, 因此备受关注, 其中空时格码的设计准则是该技术研究的核心问题。文献[1]最先给出了在平坦快衰落信道中设计空时格码的经典的距离-积准则。文献[2]根据这一准则采用计算机穷举搜索的方法得到了一些好码, 以下简称为FVY码。文献[3]针对系统中天线数较多的情况, 提出了一种比距离-积准则更优的新准则, 笔者称为最小平方欧式距离最大化准则 (以下简称为MMSED准则) , 根据这一准则文献[4]给出的CYV码是快衰落时MMSED准则下的好码 (虽然CYV码最初是为慢衰落时设计的) , 且CYV码的性能在快衰落时比FVY码更优。

笔者提出了当天线数较多时的改进设计准则, 并得到了性能为已知码中最优的新码, 还给出了快慢两种衰落条件下码性能差异原因的解释, 并将改进的设计准则应用于智贪码的设计。

《2 系统模型》

2 系统模型

一个具有n_T个发射天线、n_R个接收天线的平衰落基带系统, c $_{t}^{i}$ $_{t}^{i}$ (1≤i≤n_T, 1≤t≤l) 表示在t时隙第i根天线上发射的已调符号。在t时隙的结束时刻, 第j根 (1≤j≤n_R) 接收天线上经匹配滤波后的采样输出为 ^[1]

$r_{t}^{j} = \sqrt{E_{s}} \sum_{i = 1}^{n_{Τ}} h_{i, j} (t) c_{t}^{i} + n_{t}^{j} (1)$ $r_{t}^{j} = \sqrt{E_{s}} \sum_{i = 1}^{n_{Τ}} h_{i, j} (t) c_{t}^{i} + n_{t}^{j} (1)$

其中E_s为平均每个符号的发射能量。n $_{t}^{j}$ $_{t}^{j}$ 是t时隙第j根接收天线上的AWGN型噪声, 它具有零均值, 每维方差N₀/2。h_{i, j} (t) 是t时隙第i根发射天线与第j根接收天线之间的衰落系数, 通常假设其是对i, j独立的复高斯随机变量, 均值为0, 每维方差1/2。由于是快衰落, 所以假设h_{i, j} (t) 对t也是独立的。网格编码器的表示采用文献[3,5]中生成矩阵G的形式来表示。

《3 已有准则及其不足》

3 已有准则及其不足

笔者仅研究系统中天线数较多时 (n_T≥2, n_R≥2) 空时格码的设计问题, 因为, 一方面为了获得好的性能希望能在系统中多配置一些天线, 另一方面随着技术的发展在终端上配置2根甚至更多天线已成为可能。目前专门针对天线数较多情况下设计STTC的准则是文献[3]中提出的MMSED准则, 但是该准则仍不够完善。

设发送码字c= (c₁c₂…c_l) , 其中c_t=c¹_tc $_{t}^{2}$ $_{t}^{2}$ …c $_{t}^{n_{Τ}}$ $_{t}^{n_{Τ}}$ , 1≤t≤l。接收端最大似然接收机的判决输出码字是e= (e₁e₂…e_l) , e_t=e¹_te $_{t}^{2}$ $_{t}^{2}$ …e $_{t}^{n_{R}}$ $_{t}^{n_{R}}$ ^,1≤t≤l。显然c, e均为许用码字, c, e的取值范围仅与码G有关, 把G一定时除c=e外所有可能的 (c, e) 码字对所组成的集合记为SG。c, e之间的空时符号对汉明距离 ^[3] 即c_t≠e_t的时隙数记为δ_H (c, e) 。定义3个概念:a. 将δ_H (c, e) 在S_G上的最小值定义为码G的最小汉明距离, 记为 $D_{G} = \min_{(c, e) \in S_{G}} δ_{Η} (c, e)$ $D_{G} = \min_{(c, e) \in S_{G}} δ_{Η} (c, e)$ ;b. 将c, e之间的欧式距离的平方在S_G上的最小值定义为码G的最小平方欧式距离, 记为 $d_{G}^{2} = \min_{(c, e) \in S_{G}} | c - e |^{2} = \min_{(c, e) \in S_{G}} \sum_{t = 1}^{l} | c_{t} - e_{t} |^{2} = \min_{(c, e) \in S_{G}} \sum_{t = 1}^{l} \sum_{i = 1}^{n_{Τ}} | c_{t}^{i} - e_{t}^{i} |^{2}$ $d_{G}^{2} = \min_{(c, e) \in S_{G}} | c - e |^{2} = \min_{(c, e) \in S_{G}} \sum_{t = 1}^{l} | c_{t} - e_{t} |^{2} = \min_{(c, e) \in S_{G}} \sum_{t = 1}^{l} \sum_{i = 1}^{n_{Τ}} | c_{t}^{i} - e_{t}^{i} |^{2}$ ;c. 在所有码的最小平方欧式距离中, 将其最大值定义为最大最小平方欧式距离, 记为 $d_{\max}^{2} = \max_{所有 G} d_{G}^{2}$ $d_{\max}^{2} = \max_{所有 G} d_{G}^{2}$ 。

文献[3]中提出的最小平方欧式距离最大化 (MMSED) 准则:若码G满足D_G·n_R≥4 (实际运用中可将该条件近似转为n_T≥2且n_R≥2) , 那么具有理想信道估计的最大似然接收机将码字c误判成e的错误概率满足下式

$Ρ (c, e) \leq (\exp (- n_{R} E_{s} | c - e |^{2} / 4 Ν_{0})) / 4 (2)$ $Ρ (c, e) \leq (\exp (- n_{R} E_{s} | c - e |^{2} / 4 Ν_{0})) / 4 (2)$

也就是说c, e之间的平方欧式距离越大, 错误概率就越小。因此如果码G的d²_G=d_max², 则G是所求的好码。

不难看出以上准则中只考虑了码的最小平方欧式距离特性, 虽然具有最小平方欧式距离的码字对 (c, e) 具有最大的错误概率, 对码的整体性能有很大影响, 但这种影响并不是唯一决定性的, 其他的 (c, e) 码字对对码性能也有影响, 只不过不及前者大罢了。对于同样是MMSED准则下的多个好码, 虽然它们的最小平方欧式距离相同均为d_max², 但各个码的次小平方欧式距离可能不同, 以及在各个平方欧式距离值处所对应存在的 (c, e) 对的数目也可能不同, 因此码性能仍可能相差较大。MMSED准则正由于忽略了这一点, 从而不能有效地从该准则意义下好码的多个码中选出相对最优的好码, 因此这个准则对于寻找最优码来说显得较粗糙。 (以下“距离”均指欧式距离)

《4 准则的改进》

4 准则的改进

《4.1平方距离分布》

4.1平方距离分布

为了弥补只考虑最小平方距离的不足, 有必要将集合S_G中G的所有 (c, e) 码字对的平方距离考虑进来, 即计算 (c, e) 的平方距离在S_G上的分布, 以下简称为码G的平方距离分布。考虑到网格码中对码性能影响较大的仅是那些错误事件长度较短的 (c, e) 码字对, 因此仅考虑错误事件长度小于等于编码器约束长度+1的 (c, e) 对, 以便在分布的计算量和精确度之间取得较好的平衡。显然要获得好的性能, 平方距离分布中 (c, e) 对应尽可能多地分布在平方距离值较大处。

《4.2平方距离和方-方和比分布》

4.2平方距离和方-方和比分布

平方距离分布特性虽然较最小平方距离特性在刻画码性能方面有了提高, 但具有相同平方距离分布的码其性能仍可能有一定差异。为了能分析这一差异, 需要一个新的错误概率P (c, e) 上界。

由文献[1]知, 在信道估计理想时, 将c误判成e的错误概率为

$\begin{array}{l} Ρ (c, e | h_{i, j}, i = 1, 2, \dots, n_{Τ}, j = 1, 2, \dots, \\ n_{R}) \leq (\exp (- d^{2} (c, e) E_{s} / 4 Ν_{0})) / 2 (3) \\ d^{2} (c, e) = \sum_{t = 1}^{l} \sum_{j = 1}^{n_{R}} | β_{j} (t) |^{2} | c_{t} - e_{t} |^{2} (4) \end{array}$ $\begin{array}{l} Ρ (c, e | h_{i, j}, i = 1, 2, \dots, n_{Τ}, j = 1, 2, \dots, \\ n_{R}) \leq (\exp (- d^{2} (c, e) E_{s} / 4 Ν_{0})) / 2 (3) \\ d^{2} (c, e) = \sum_{t = 1}^{l} \sum_{j = 1}^{n_{R}} | β_{j} (t) |^{2} | c_{t} - e_{t} |^{2} (4) \end{array}$

其中|β_j (t) |²是对j, t独立且同分布的中心χ²型随机变量, 均值方差都为1。

当δ_H (c, e) n_R≥4时 (该条件可近似转化为n_T≥2且n_R≥2) , 式 (4) 可近似认为是一系列独立同分布的随机变量之和, 由中心极限定理知, 该和式近似满足高斯分布, 其均值为u= $n_{R} \sum_{t = 1}^{l} | c_{t} - e_{t} |^{2} ‚$ $n_{R} \sum_{t = 1}^{l} | c_{t} - e_{t} |^{2} ‚$ 方差为 $σ^{2} = n_{R} (\sum_{t = 1}^{l} (| c_{t} - e_{t} |^{2})^{2})$ $σ^{2} = n_{R} (\sum_{t = 1}^{l} (| c_{t} - e_{t} |^{2})^{2})$ 。再令R=E_S/4N₀, 则可得到

$\begin{array}{l} Ρ (c, e) \leq \frac{1}{2} \int_{0}^{\infty} e x p (- R x) \frac{1}{\sqrt{2 π} σ} \cdot \\ \exp (- \frac{(x - u)^{2}}{2 σ^{2}}) d x = \\ \frac{1}{2} Q (\frac{σ^{2} R - u}{σ}) \exp (\frac{σ^{2} R^{2}}{2} - u R) (5) \end{array}$ $\begin{array}{l} Ρ (c, e) \leq \frac{1}{2} \int_{0}^{\infty} e x p (- R x) \frac{1}{\sqrt{2 π} σ} \cdot \\ \exp (- \frac{(x - u)^{2}}{2 σ^{2}}) d x = \\ \frac{1}{2} Q (\frac{σ^{2} R - u}{σ}) \exp (\frac{σ^{2} R^{2}}{2} - u R) (5) \end{array}$

由于x>1时Q (x) < (2π) ^-1/2x^-1exp (-x²/2) 且一般有σ/ (Rσ²-u) <1/R, 那么由式 (5) 得到P (c, e) 的新上界为

$\begin{array}{l} Ρ (c, e) < (8 π)^{- 1 / 2} R^{- 1} \exp (- u^{2} / 2 σ^{2}) = \\ \frac{4 Ν_{0}}{\sqrt{8 π} E_{s}} \exp (- \frac{n_{R}}{2} (\sum_{t = 1}^{l} | c_{t} - e_{t} |^{2})^{2} / \\ \sum_{t = 1}^{l} (| c_{t} - e_{t} |^{2})^{2}) (6) \end{array}$ $\begin{array}{l} Ρ (c, e) < (8 π)^{- 1 / 2} R^{- 1} \exp (- u^{2} / 2 σ^{2}) = \\ \frac{4 Ν_{0}}{\sqrt{8 π} E_{s}} \exp (- \frac{n_{R}}{2} (\sum_{t = 1}^{l} | c_{t} - e_{t} |^{2})^{2} / \\ \sum_{t = 1}^{l} (| c_{t} - e_{t} |^{2})^{2}) (6) \end{array}$

可见式 (6) 也是当系统中天线数较多时评判码性能优劣的一种度量, 比值

$u^{2} / n_{R} σ^{2} = (\sum_{t = 1}^{l} | c_{t} - e_{t} |^{2})^{2} / \sum_{t = 1}^{l} (| c_{t} - e_{t} |^{2})^{2}$ $u^{2} / n_{R} σ^{2} = (\sum_{t = 1}^{l} | c_{t} - e_{t} |^{2})^{2} / \sum_{t = 1}^{l} (| c_{t} - e_{t} |^{2})^{2}$

越大, 则误判概率就越小。该比值的分子是对平方距离|c_t-e_t|²先按时间求和然后再平方, 即平方距离的“和方”, 分母是对平方距离|c_t-e_t|²先平方然后再按时间求和, 即平方距离的“方和”, 该比值简称为平方距离和方/方和比。与4.1节所述类似, 仅考虑平方距离和方/方和比的最小值是不全面的, 应当计算码G所有 (c, e) 对的平方距离和方/方和比在S_G上的分布。当多个码的平方距离分布相同时, 可以再用其平方距离和方/方和比分布对这些码做进一步的比较。

例如, n_T=2, 8状态、4PSK调制的4个码Code1…Code4的生成矩阵见表1, 码的特性见表2, 性能的仿真曲线见图1, 仿真中l取130。

从表2中看出这4个码均为MMSED准则意义下的好码, 但图1显示出这些码之间存在着明显的性能差异。表2中Code1, Code2具有完全相同的平平方距离分布与平方距离和方/方和比分布, 因而图1中反映出两者的性能几乎完全相同。Code3虽然与Code1, Code2平方距离分布相同, 但Code3的平方距离和方/方和比分布更优, 性能相对有所提高。而Code4不仅与Code1, Code2, Code3在平方距离和方/方和比分布上不同, 更重要的是Code4具有更优的平方距离分布, 图1中反映出该码的性能也因此提高得更显著, 是4个码中最优的。所以平方距离分布特性对码性能的影响是主要的, 平方距离和方/方和比分布的影响是次要的, 仅用于当平方距离分布相同时对码做进一步细分。因为上界式 (6) 是相当宽松的, 对平方距离分布不同的码, 该界的松紧程度也相差较大, 平方距离和方/方和比分布不能用来比较平方距离分布不同的码。

表1 码的生成矩阵

Table 1 The generation matrixes of codes

《表1》

Code1

Code2

Code3

Code4

New

n_T=2, 8状态

n_T=2

n_T=3

4状态

8状态

16状态

32状态

64状态

8状态

[\begin{matrix} 0 & 2 \\ 2 & 0 \\ 2 & 2 \\ 1 & 1 \\ 1 & 1 \end{matrix}]

$[\begin{matrix} 0 & 2 \\ 2 & 0 \\ 2 & 2 \\ 1 & 1 \\ 1 & 1 \end{matrix}]$

[\begin{matrix} 0 & 2 \\ 2 & 0 \\ 2 & 2 \\ 1 & 1 \\ 1 & 3 \end{matrix}]

$[\begin{matrix} 0 & 2 \\ 2 & 0 \\ 2 & 2 \\ 1 & 1 \\ 1 & 3 \end{matrix}]$

[\begin{matrix} 0 & 2 \\ 2 & 1 \\ 2 & 2 \\ 0 & 1 \\ 1 & 1 \end{matrix}]

$[\begin{matrix} 0 & 2 \\ 2 & 1 \\ 2 & 2 \\ 0 & 1 \\ 1 & 1 \end{matrix}]$

[\begin{matrix} 0 & 2 \\ 2 & 1 \\ 2 & 2 \\ 1 & 1 \\ 0 & 2 \end{matrix}]

$[\begin{matrix} 0 & 2 \\ 2 & 1 \\ 2 & 2 \\ 1 & 1 \\ 0 & 2 \end{matrix}]$

[\begin{matrix} 0 & 2 \\ 2 & 1 \\ 1 & 2 \\ 2 & 0 \end{matrix}]

$[\begin{matrix} 0 & 2 \\ 2 & 1 \\ 1 & 2 \\ 2 & 0 \end{matrix}]$

[\begin{matrix} 1 & 2 \\ 2 & 0 \\ 2 & 2 \\ 2 & 1 \\ 0 & 2 \end{matrix}]

$[\begin{matrix} 1 & 2 \\ 2 & 0 \\ 2 & 2 \\ 2 & 1 \\ 0 & 2 \end{matrix}]$

[\begin{matrix} 1 & 2 \\ 2 & 0 \\ 3 & 3 \\ 2 & 2 \\ 1 & 2 \\ 2 & 0 \end{matrix}]

$[\begin{matrix} 1 & 2 \\ 2 & 0 \\ 3 & 3 \\ 2 & 2 \\ 1 & 2 \\ 2 & 0 \end{matrix}]$

[\begin{matrix} 1 & 2 \\ 2 & 0 \\ 2 & 1 \\ 1 & 0 \\ 2 & 0 \\ 2 & 2 \\ 1 & 2 \end{matrix}]

$[\begin{matrix} 1 & 2 \\ 2 & 0 \\ 2 & 1 \\ 1 & 0 \\ 2 & 0 \\ 2 & 2 \\ 1 & 2 \end{matrix}]$

[\begin{matrix} 1 & 2 \\ 2 & 1 \\ 0 & 2 \\ 0 & 1 \\ 0 & 2 \\ 2 & 0 \\ 2 & 1 \\ 1 & 2 \end{matrix}]

$[\begin{matrix} 1 & 2 \\ 2 & 1 \\ 0 & 2 \\ 0 & 1 \\ 0 & 2 \\ 2 & 0 \\ 2 & 1 \\ 1 & 2 \end{matrix}]$

[\begin{matrix} 1 & 2 & 2 \\ 2 & 0 & 3 \\ 2 & 3 & 2 \\ 2 & 2 & 0 \\ 0 & 2 & 3 \end{matrix}]

$[\begin{matrix} 1 & 2 & 2 \\ 2 & 0 & 3 \\ 2 & 3 & 2 \\ 2 & 2 & 0 \\ 0 & 2 & 3 \end{matrix}]$

表2 n_T=2, 8状态 4PSK调制的4个码的特性

Table 2 The characteristics of 4, 8-state, 4PSK modulated codes when n_T=2

《表2》

码	平方距离分布																							d_max²取值
	平方距离			12			14			16		18			20			24			26
Code1, Code2				10 240			0			11 264		0			6 144			4 096			0
Code3	分布的 (c, e) 对数目			10 240			0			11 264		0			6 144			4 096			0			12
Code4				3 072			12 288			6 144		2 048			5 120			1 024			2 048
码	平方距离和方/方和比分布
	比值	1.80	2.57		2.67	2.79		2.88	2.91		3.00		3.33	3.56		3.57	3.60		3.76	3.77		3.79	3.85		4.00
Code1, Code2		3 072	0		7 168	0		0	0		7 168		0	0		6 144	4 096		0	0		0	0		4 096
Code3	(c, e) 对数目	3 072	5 120		2 048	0		0	5 120		0		3 072	4 096		1 024	3 072		0	0		3 072	2 048		0
Code4		3 072	0		2 048	2 048		8 192	0		0		0	4 096		1 024	1 024		2 048	4 096		0	4 096		0

《图1》

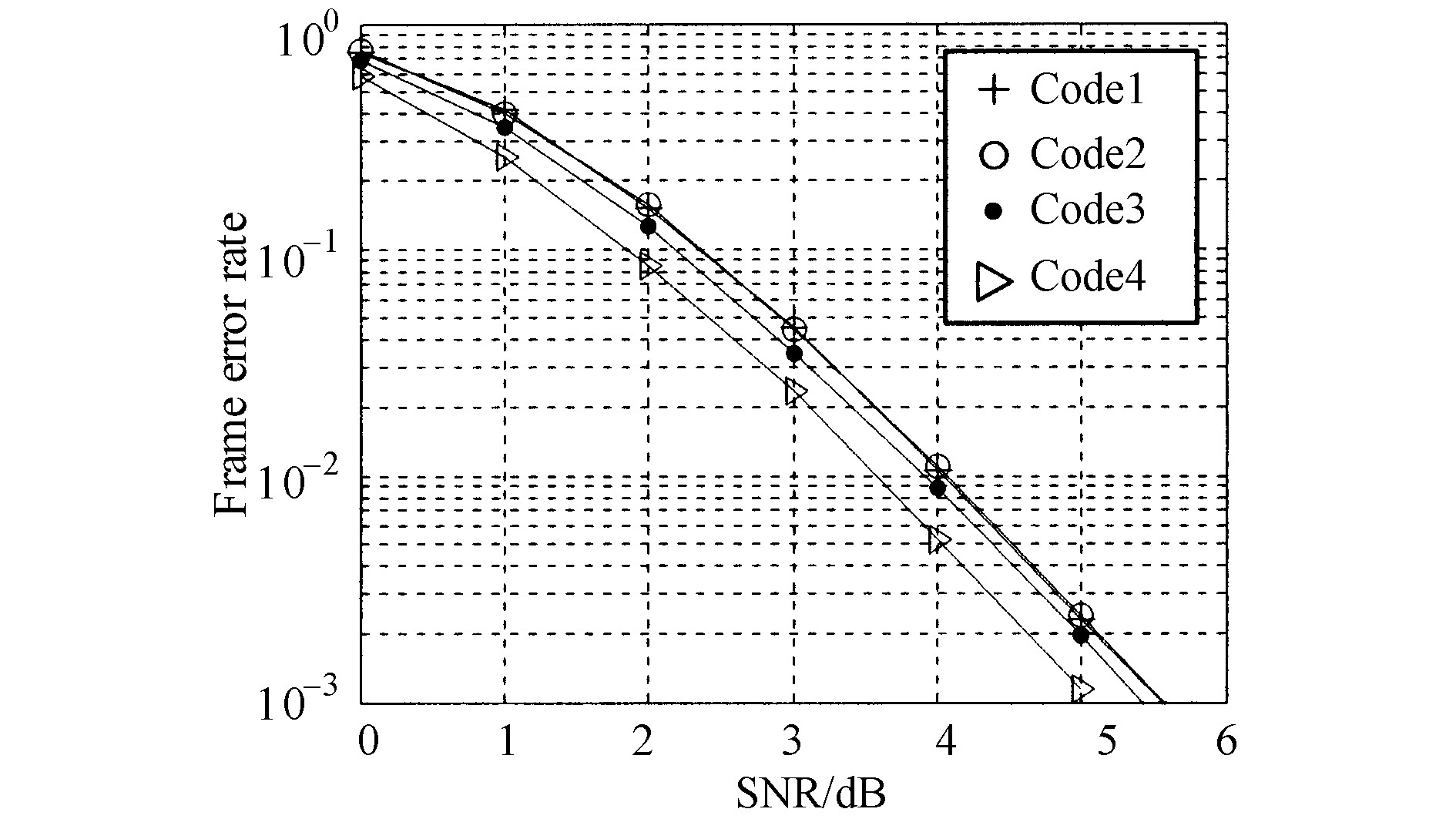
图1 n_T=2, 8状态 4PSK调制的4个码的误帧率 (n_R=4)

Fig.1 The FER of 4, 8-state, 4PSK modulated codes when n_T=2, n_R=4

《4.2.1 改进的准则》

4.2.1 改进的准则

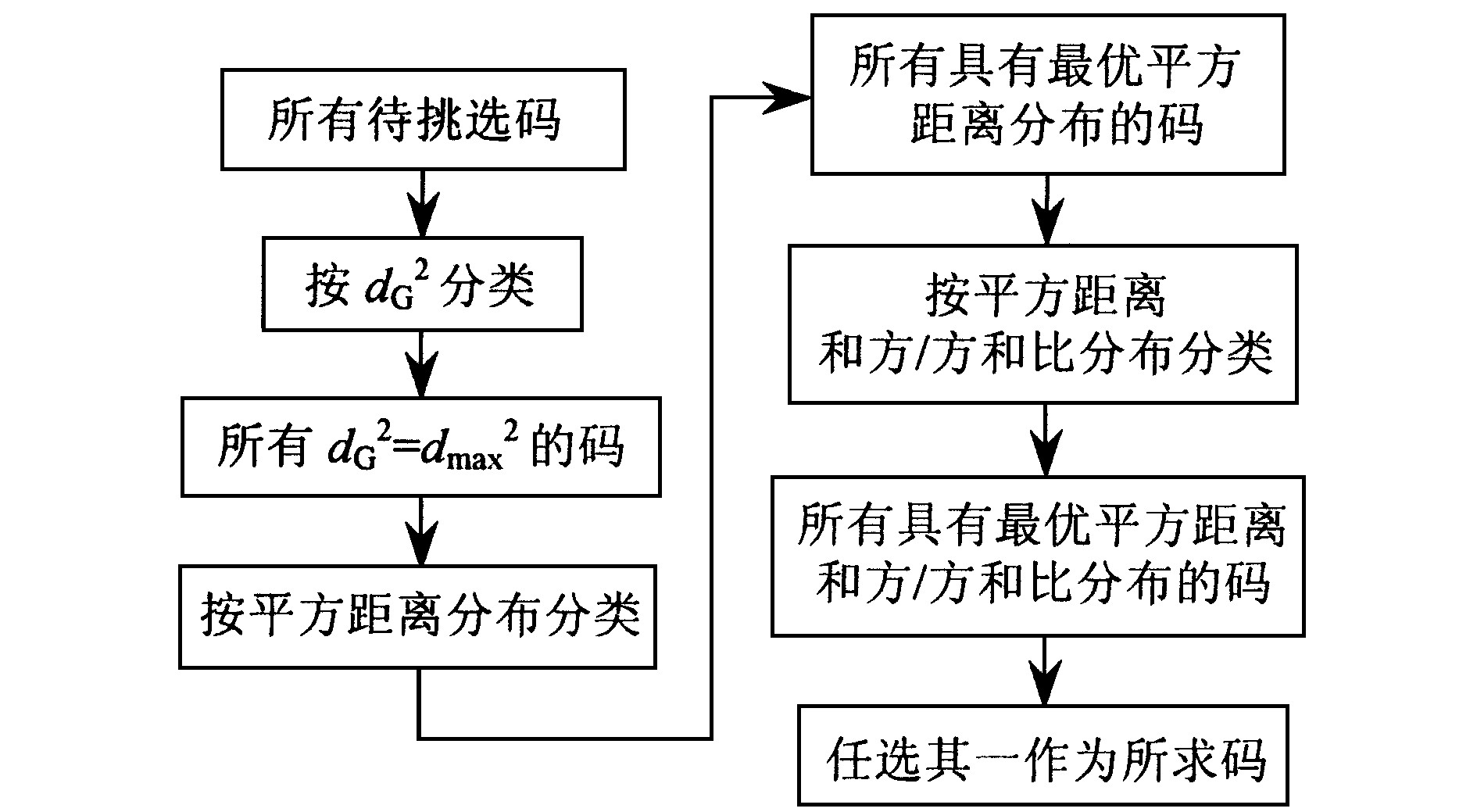
快衰落时改进的STTC的设计准则:在平坦快衰落信道中, 当n_T≥2且n_R≥2时, 第1步选出所有最小平方距离达到最大值的码, 第2步对这些码按平方距离分布进行分类, 第3步再对具有最优平方距离分布的码按平方距离和方/方和比分布做进一步细分, 第4步找出上述2次分类后的最优类型及相应的码。对于因两个分布均相同而同属最优类型的多个码, 可以从中任选其一作为最优码。准则的流程图如图2所示。

《图2》

图2 改进准则的流程图

Fig.2 The flowchart of the improved criterion

在慢衰落且天线数较多时, 已有的设计准则是迹准则 ^[3,4]。通过比较不难看出, 快衰落时的MMSED准则与慢衰落时的迹准则两者的不足之处是类似的, 改进思路也是相似的, 这里不再详述, 仅列出不同之处于下:快衰落时码性能的主要决定因素是平方距离分布, 而慢衰落时是迹分布, 这里的迹分布指的是A (c, e) 的迹在S_G上的分布, 其中矩阵A (c, e) 由文献[1]定义。但由文献[3]知 $\sum_{t = 1}^{l} \sum_{i = 1}^{n_{Τ}} | c_{t}^{i} - e_{t}^{i} |^{2} = t r$ $\sum_{t = 1}^{l} \sum_{i = 1}^{n_{Τ}} | c_{t}^{i} - e_{t}^{i} |^{2} = t r$ (A (c, e) ) , 故同一个码快衰落时的平方距离分布与慢衰落时的迹分布在数值上是相等的;码性能的次要决定因素在快衰落时是平方距离和方/方和比分布, 在慢衰落时是特征值和方/方和比分布, 这里的特征值指的是A (c, e) 的特征值 (两种分布数值上不等) 。

《4.2.2 码搜索方法》

4.2.2 码搜索方法

文献[6]提出了一种在不丢失好码的前提下减少搜索量的快速穷举搜索方法, 由其证明过程不难看出这种快速搜索方法对改进准则仍然适用, 这里就采用这种方法。

同一个码在快衰落时的平方距离分布与其在慢衰落时的迹分布在数值上完全相同, 因此可以利用慢衰落时好码搜索过程的一些中间结果, 以减少搜索计算量。

《5 设计实例》

5 设计实例

假设调制方式均采用4PSK (所有码的2个分布特性均不再列出) , 各状态的生成矩阵见表1。

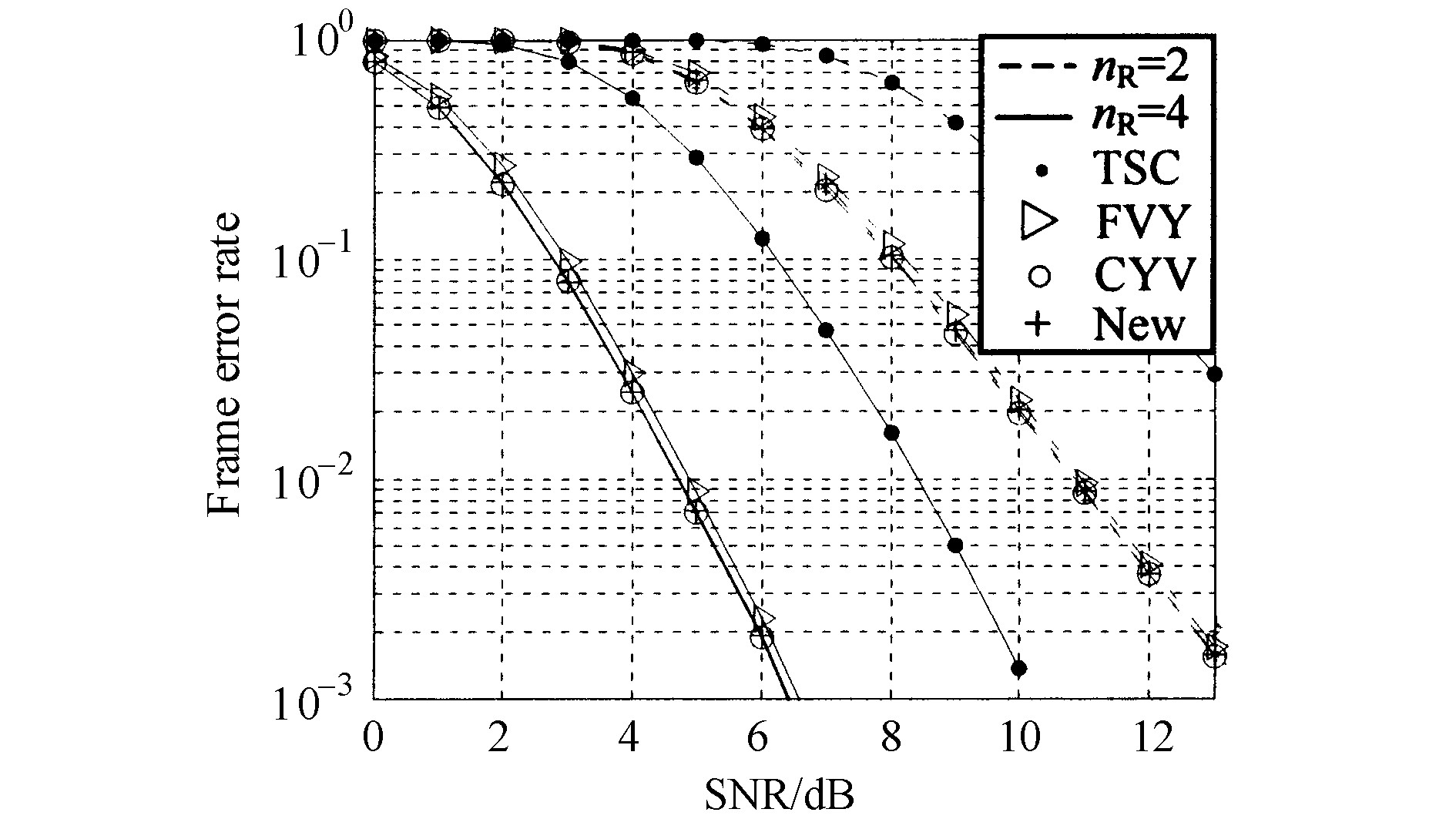
n_T=2的情况。从最基本的4状态开始, 经搜索找到了新的最优码New, 性能曲线见图3。图3中还给出了另3种典型码FVY, CYV和TSC ^[1]的性能曲线作为参考。从图3中可以看出, New码与CYV码同为最优码 (两者的性能差别极小可以忽略) , 这是由于它们虽然生成矩阵不同, 但2个分布完全相同。然而, 在4状态时根据改进准则所找到的新码并不像所期待的那样, 性能优于依MMSED准则得到的CYV码, 而仅仅是与CYV码同为最优, 因为改进准则实际是对MMSED准则下的所有好码按2个分布不同作进一步分类, 准确、高效地找出其中的最优类型和相应的最优码。当状态数为4时, 所有MMSED准则下的好码按2个分布分类后仅有4类, 由于类型数太少, 按改进准则找到的新码与文献[3]按MMSED准则所提出的CYV码, 恰好属同一类型, 两者性能上相同。

《图3》

图3 n_T=2, 4状态的4个码的误帧率

Fig.3 The FER of 4, 4-state codes when n_T=2

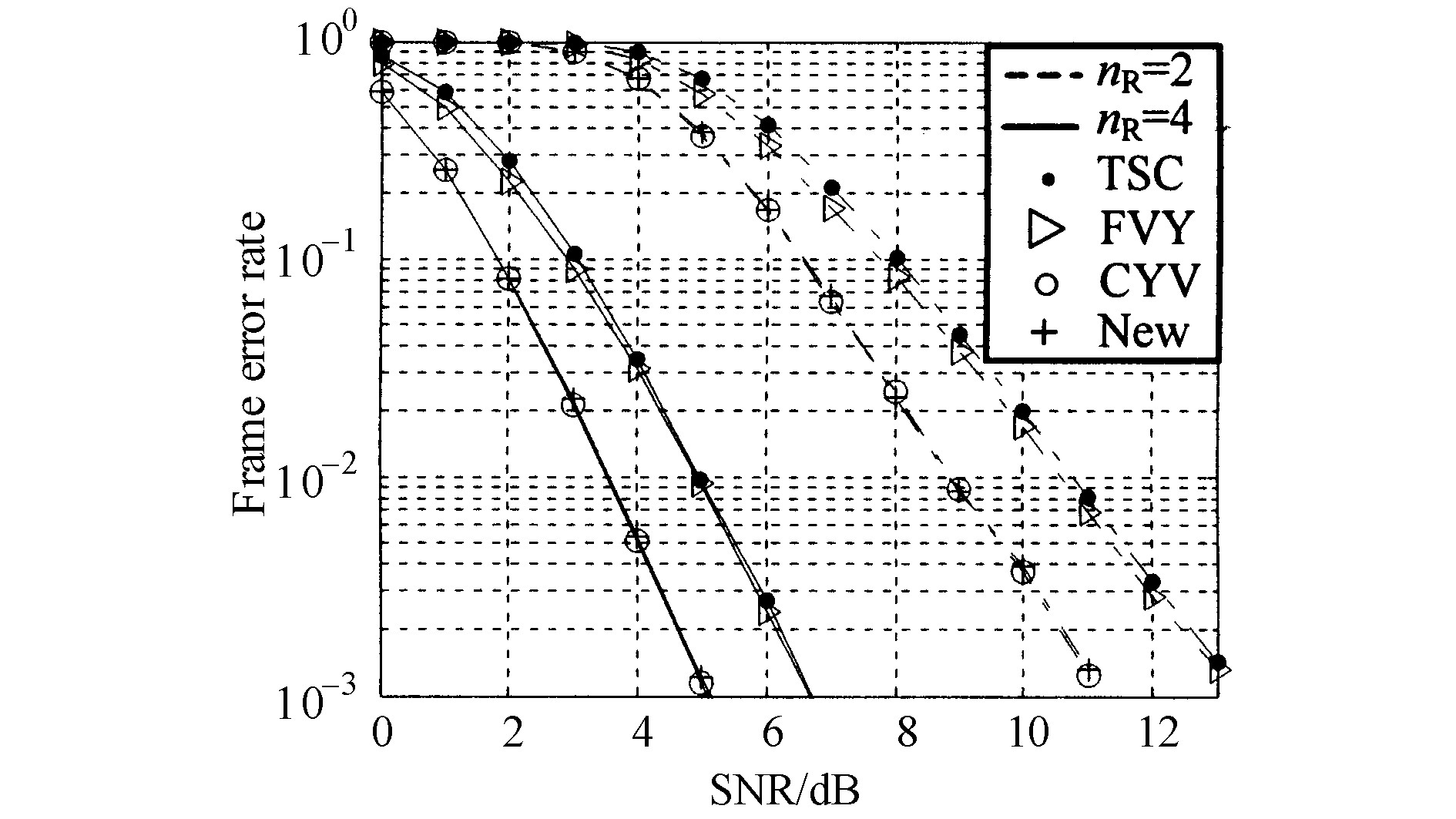
对于8状态找到了性能与CYV同为最优的新码, 性能曲线见图4。

《图4》

图4 n_T=2, 8状态的4个码的误帧率

Fig.4 The FER of 4, 8-state codes when n_T=2

对于16状态, 同样找到了新码, 与4状态时相似, 新码的性能与CYV码同为最优, 2个码的2个分布完全相同。出现这种现象的原因和4状态时相同, 经2次分类后的类型数只有5种。

在32状态, 新码较TSC, FVY码的性能增益分别在1.5 dB和2 dB以上, 与CYV码相比, 在FER为10^-3处也有约0.5 dB优势, 性能曲线见图5, n_R=2。

《图5》

图5 n_T=2, 32状态的4个码的误帧率

Fig.5 The FER of 4, 32-state codes when n_T=2

在64状态时, 新码相对于CYV码的优势并不十分明显 (其原因与未能穷尽搜索有关) , 如图6所示 (此时TSC和FVY码不存在) 。

在n_T≥3的情况, 待搜索检验的码数量庞大。以8状态、n_T=2的新码为基础, 采用文献[7]中的方法搜索8状态、n_T=3时的好码。虽然搜索方法是次优的, 但仍找到了略优于CYV ^[7]的新码, 性能曲线见图7 (不存在TSC, FVY码) n_R=2。

《图6》

图6 n_T=2, 64状态的2个码的误帧率

Fig.6 The FER of 2, 64-state codes when n_T=2

《图7》

图7 n_T=3, 8状态的2个码的误帧率

Fig.7 The FER of 2, 8-state codes when n_T=3

目前已知的其他快衰落时的好码还有SO ^[8]码和ZQW ^[9]码 (仅当n_T=2时存在) 。仿真结果表明, SO码在4状态, 4PSK调制时性能与New相同, 但在8状态、8PSK调制时性能较差, 甚至还不及FVY;对于ZQW码, 在4状态和16状态时该码的性能在整个仿真区间FER∈[0.001 1]内均与New十分接近, 而在8状态和32状态时, 其性能明显不及New。所有的仿真结果说明, 新码的性能是目前已知码中最优的。

《6 相关应用》

6 相关应用

《6.1快慢衰落下码性能差异原因的新解释》

6.1快慢衰落下码性能差异原因的新解释

笔者发现同一个码一般在快衰落环境下的性能要比在慢衰落环境下好一些, 以前面提到的n_T=2, 8状态、4PSK调制的3个码为例, 在2种环境下的性能曲线见图8 (n_R=4) , 对于New和CYV码, 快、慢衰落时的性能差距在1.8 dB左右, 对于TSC约0.8 dB。

《图8》

图8 快、慢衰落环境下码性能的比较

Fig.8 The performance comparison between in fast and slow fading channels

这种现象直观上可解释为快衰落时各个不同时隙衰落不相关, 有时间分集的效果, 但从P (c, e) 上界的角度可给出一个新的解释。由于同一个码的平方距离分布和迹分布相等, 因此码在快、慢两种衰落下的性能差异并不是由主要决定因素所致, 而是来自于次要决定因素的不同。当快衰落时P (c, e) 的上界为式 (6) , 据此得到了码性能的次要决定因素为平方距离和方/方和比分布;同理, 当慢衰落时可类似地推得

$Ρ (c, e) < \frac{4 Ν_{0}}{\sqrt{8 π} E_{s}} \exp (- \frac{n_{R}}{2} (\sum_{i = 1}^{n_{Τ}} λ_{i})^{2} / \sum_{i = 1}^{n_{Τ}} λ_{i}^{2}) (7)$ $Ρ (c, e) < \frac{4 Ν_{0}}{\sqrt{8 π} E_{s}} \exp (- \frac{n_{R}}{2} (\sum_{i = 1}^{n_{Τ}} λ_{i})^{2} / \sum_{i = 1}^{n_{Τ}} λ_{i}^{2}) (7)$

其中λ_i为A (c, e) 的特征值 ^[1], 据此可以得到慢衰落时码性能的次要决定因素为特征值和方/方和比分布。这2个比值分布的不同可以解释同一个码在不同衰落速度下性能差异的原因。以n_T=2, 8状态的New码为例, 其快、慢衰落下的2个比值分布见表3, 可见快衰落时的比值总体上比慢衰落时大, 性能更好 (图8) 。

表3 快慢衰落下两种比值分布的比较

Table 3 The comparison of two distributions between in fast and slow fading channels

《表3》

码 New	平方距离或特征值和方/方和比分布
码 New	比值区间	[1.0, 1.4)	[1.4, 1.8)	[1.8, 2.0)	[2.0, 3.0)	[3.0, 3.9)
Slow	(c, e) 对	10 464	15 104	6 176	0	0
Fast	数目	0	0	3 072	8 192	20 480

当图8的信噪比小于等于2时, TSC码在慢衰落时的性能反而明显优于快衰落时的性能, 是一个例外。因为信噪比R太小, 将使R<u/σ²即σ²R-u<0, 导致式 (5) 中的Q函数不能用近似表达式展开, 使得上界式 (6) 不能成立。特别对于TSC这种性能较差的码, 虽然其u²/σ²较小, 但u/σ²却较其他码更大, 更容易使σ²R-u<0的情况出现。对于慢衰落时的式 (7) 也同样存在这个问题。由于信噪比太小, 式 (6) 和式 (7) 已不能再作为码性能比较的依据, 快衰落时性能也就不再优于慢衰落的。

《6.2智贪码的设计》

6.2智贪码的设计

在文献[1]中提出了智贪码 (smart greedy code) 的概念, 它也是空时码的一种, 其特点是该类码既是快衰落下的好码也是慢衰落下的好码 (但并不要求两种衰落下均为最优) 。其设计思路:将慢衰落时的秩-行列式准则与快衰落时的距离-积准则相结合, 从而保证在两种衰落下均为好码。

一种设计智贪码的新方法。当n_T≥2且n_R≥2时, 快、慢2种衰落下对码性能起主要决定作用的分别是平方距离分布和迹分布, 且对于同一个码这2种分布数值上相等。所以一种衰落下的最优码在另一种衰落下性能也一定很好 (但不一定最优, 这是因为快衰落时的最优码, 其在慢衰落时的特征值和方/方和比分布不一定最优, 反之亦然) , 这符合智贪码的要求。实践表明在发射天线数、状态数较小时, 如n_T=2, 4, 和8状态时, 2种衰落下的最优码往往相同;而当发射天线数、状态数较大时, 比如n_T≥3时, 则一般不同, 但性能相差很小。因此设计智贪码的新方法, 是任意选取改进准则得到的快或慢衰落下的最优码作为智贪码。例如, 当n_T=2, 8状态时, 快衰落下的最优码New (见表1) , 选其作为智贪码, 性能曲线见图8, 该码在两种衰落下均性能最优, 满足了在不同衰落速度下均为好码的要求, 是所求的智贪码。

《7 结语》

7 结语

在平坦快衰落条件下, 当n_T≥2, n_R≥2时, 给出了设计STTC的改进准则:平方距离分布准则与平方距离和方/方和比分布准则, 前者对码性能起主要决定作用, 后者起次要决定作用。依此改进准则找到了一些新码, 其性能为已知码中最优的。给出了P (c, e) 的一个新的上界, 该上界从新的角度解释了同一个码在快、慢2种衰落下存在性能差异的原因。另外由于同一个码在快衰落时的平方距离分布与慢衰落时的迹分布数值上相等, 且都对码性能起主要决定作用, 因而以此为依据设计在快、慢衰落下均具有良好性能的智贪码。

展示更多