薄膜润滑径向轴承特性分析

摘要

薄膜润滑轴承的特性远不同于常规轴承，在考虑间隙对润滑剂产生的影响后，润滑剂的特性将发生较大的变化。由于这种变化，薄膜润滑的特性才被广泛地研究和重视。文章应用等效粘度修正模型对径向滑动轴承进行了性能分析,对无限宽轴承可得出压力计算的解析表达式,从而可精确地计算轴承的性能。

正文

薄膜润滑现象在许多条件下都可能产生,近年来,对它的研究也日深增加,出现了多种计算模型。例如曲庆文等提出的等效粘度模型^[1,2],把同一间隙截面内的粘度统计处理为平均粘度,此种模型可以通过相对简单的间隔变化实验来测定平均粘度统计形成;Tichy等提出的、由曲庆文等进一步推导的分层粘度模型^[3,4],把流层分为三个固定层,以层内等粘度处理,其困难在于层的划分,层是通过润滑剂与固体表面的特性进行统计计算得到的;曲庆文等提出的指数型粘度模型^[5,6],遵循吸附层内粘度是连续变化的规律,并总结上述两种情形的粘度变化规律,进行模拟统计的结果;张朝辉等提出了三角函数模型^[7],并进行了轴承的分析计算,也得到较理想的结果。这些模型主要用于计算推力轴承的承载能力和摩擦阻力,对于一般的工程计算,几乎可以等同应用。笔者拓展到径向轴承的计算,将以等效粘度修正模型为基础进行径向溯动轻承的性能分析,以得到薄膜润滑条件下径向轴承性能计算的基本公式,为薄膜润滑轴承的应用提供理论基础。

《1 广义雷诺方程及无量纲化》

1 广义雷诺方程及无量纲化

在无限宽不可压缩的稳态条件下,不考虑体积力、惯性力的影响,旦为层流状态,则广义雷诺方程可写为

\(\frac{\partial}{\partial x}\left(J \frac{\partial p}{\partial x}\right)=U \frac{\partial}{\partial x}\left(\frac{J_{1}}{J_{0}}\right)\) (1)

式中\(J_{n}=\int_{0}^{h} \frac{z^{n}}{\eta} \mathrm{d} z, n=0,1, J=\int_{0}^{h} \frac{z}{\eta}\left(z-\frac{J_{1}}{J_{0}}\right) \mathrm{d} z\),其中h为润滑油膜厚度,η为润滑剂粘度,是油膜厚度和服附层厚度的函数,其关系为 (2)

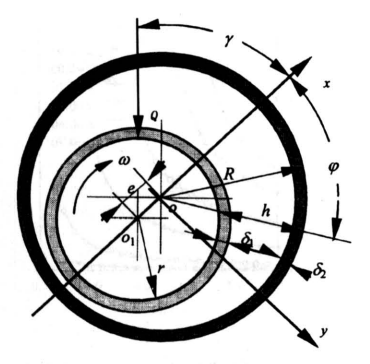
式中\(\eta_{0}\)为常规的润滑剂粘度,δ为紧密吸附层厚度,根据粘性吸附理论,紧密吸附层厚度与相互作用表面的性质有关。现在分析径向滑动轴承,轴承结构参数如图1,采用极坐标,则x=Rψ,dx=Rdψ,h=c(1+ε cos ψ),把式(2)和上述关系代入式(1),积分一次得

\(\frac{\partial p}{\partial \varphi}=\frac{6 \eta_{0} \omega}{\psi^{2}} \frac{\varepsilon \cos \varphi+C_{1}}{(1+\varepsilon \cos \varphi)^{2}(1+\varepsilon \cos \varphi-2 \delta / c)}\) (3)

式中ψ=c/R,ε=e/c,c=R-r,ψ为相对间陶,ε为偏心率,e为偏心距,Ci为常数。

由式(3)令\(p=\frac{6 \eta_{0} \omega}{\psi^{2}} p^{*}, \quad \delta^{*}=\frac{\delta}{c}, \quad \delta^{*}\)称为

《图1》

图1 径向轻承结构

Fig.1 Structure sketch of journal bearing

无量纲紧密吸附层厚度,为计算方便起见,采用半Sommerfeld边界条件,即\(\varphi=0, p^{*}=0 ; \varphi=\pi \sim 2 \pi, p^{*}=0\), (4)

\(p^{*}=\frac{1}{\left(1-\varepsilon^{2}-\bar{h}_{s}\right) \sqrt{1-\varepsilon^{2}}}\left\{\left[\left(1+\frac{\varepsilon}{A}\right) .\right.\right. \\ \left.\frac{\beta}{\sqrt{1-A^{2}}}-\frac{\varepsilon \gamma}{A}\right]+\frac{C_{1}-1}{\left(1-\varepsilon^{2}-\bar{h}_{s}\right)\left(1-\varepsilon^{2}\right)} \\ \left.\left[\left(1+\frac{\varepsilon}{A}\right)^{2} \frac{\beta}{\sqrt{1-A_{2}}}-\left(\frac{2 \varepsilon}{A}+\frac{\varepsilon^{2}}{A^{2}}\right) \gamma+\frac{\varepsilon^{2}}{A} \sin \gamma\right]\right\}\) (5)

式中\(\begin{array}{l} C_{1}=1 \frac{A\left(A+\varepsilon-\varepsilon \sqrt{\left.1-A^{2}\right)\left(1-\varepsilon^{2}\right)}\right.}{\left.(A+\varepsilon)^{2}-\varepsilon(2 A+\varepsilon) \sqrt{1-A^{2}}\right)}, \\ A=\frac{\delta^{*} \varepsilon}{1-\varepsilon^{2}-\delta^{*}}, \cos \gamma=\frac{\varepsilon+\cos \varphi}{1+\varepsilon \cos \varphi}, \\ \cos \beta=\frac{A+\cos \gamma}{1+A \cos \gamma^{\circ}} \end{array}\)

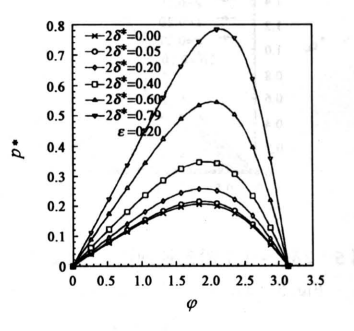
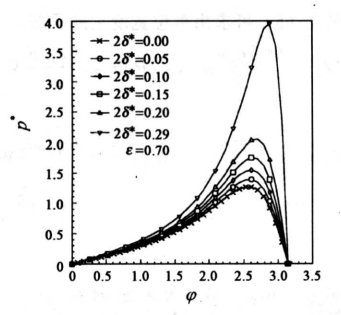
由此式可知,cos ψ、cosγ、cosβ在0、π和2π时有相同的值。根据式(5)可以得出无量纲压力p*与无量纲吸附层厚度2σ*和偏心率ε的关系。图2和图3分别为ε=0.2和ε=0.7时不同2σ*下无量纲压力p*的变化曲线(图中角度ψ以弧度表示,下同)。在计算中,要保证ε+2σ*<1,即在计算时始终要有流动的液体膜存在。在分子级润滑时,当无量纲液体膜厚度近于1时,涧潜剂将会产生相变,形成液晶态结构,从而改变了润滑剂的特性。在薄膜润滑条件下,油膜压力随无量纲紧密吸附层厚度的增大而增大。

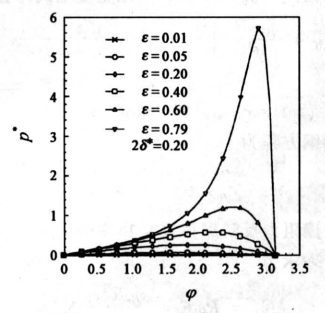
图4和图5分别为2σ*=0.2和2σ*=0.7时不同偏心率下的压力变化规律。每一条曲线都与不考虑服附时的变化规律基本一致。随着ε的增大,最大压力点的位置逐渐靠近油膜出口,且急剧增大。

《图2》

图2 ε=0.2时无量纲压力p*的变化规律

Fig.2 The non-dimensional pressure p* at ε=0.2

《图3》

图3 ε=0.7时无量纲压力p*的变化规律

Fig.3 The non-dimensional pressure p* at ε=0.7

《图4》

图4 2σ*=0.2时无量线压力p*的变化规律

Fig.4 The non-dimensional pressure P* at 2σ*=0.2

《图5》

图5 2σ*=0.7时无量纲压力p“的变化规律

Fig.5 The non-dimensional pressure p* at 2σ*= 0.7

《2 承载能力与摩擦特性》

2 承载能力与摩擦特性

据式(5)可求出单位宽度上的承载能力,即\(W_{x}=\int_{0}^{\pi} \frac{6 \eta_{0} \omega}{\psi^{2}} p^{*} \cos \varphi R \mathrm{~d} \varphi=\frac{6 \eta_{0} \omega R}{\psi^{2}} W_{x}^{*}, \), (6)

同理:

\(W_{y}=\frac{6 \eta_{0} \omega R}{\psi^{2}} \int_{0}^{\pi} p^{*} \sin \varphi \mathrm{d} \varphi=\frac{6 \eta_{0} \omega R}{\psi^{2}} W_{y}^{*}\), (7)

\(W=\frac{6 \eta_{0} \omega R}{\psi^{2}} \sqrt{W_{x}^{* 2}+W_{y}^{* 2}}=\frac{6 \eta_{0} \omega R}{\psi^{2}} W^{*}\) (8)

式中W_x^*、W_y^*、W^*为无量网承载能力,由式

(8)可计算出W*与无量纲吸附层厚度2σ*和偏心率ε的关系。从图6中可知,当ε+2σ*近于1时,承载能力急剧增加,即达到了相变点。

根据流体润滑理论,单位宽度上的摩擦阻力为

\(\begin{array}{c} F_{h, 0}=\frac{\eta_{0} \omega R}{\psi}\left[\int_{0}^{2 \pi}-\frac{\mathrm{d} \varphi}{1+\varepsilon \cos \varphi-2 \delta^{*}} \pm 3 \cdot\right. \\ \left.\int_{0}^{\pi} \frac{\varepsilon \cos \varphi+C_{1}}{(1+\varepsilon \cos \varphi)\left(1+\varepsilon \cos \varphi-2 \delta^{*}\right)} \mathrm{d} \varphi\right] \end{array}\), (9)

其无量纲方程为：\(F_{h, 0}=\frac{\eta_{0} \omega R}{\psi} F_{h, 0}^{*}\) （10）

摩擦阻力反映摩擦损耗功率的大小,摩擦损耗功率可表示为

\(N_{f}=R \omega F=\frac{\eta_{0} R^{2} \omega^{2}}{\psi} N_{f}^{*}\) (11)

由于在一般条件下,运动表面的摩擦力大于静摩擦面的摩擦力,所以,以下的分析只以动表面的无量纲摩擦力为准。如图7所示,F^*=F_h^*。

《图6》

图6 无量纲承载能力W^*与2σ*和ε的变化规律

Fig.6 The non-dimensional load capacity of the bearing as a function of (a) the adsorbed layer thickness and (b) the eccentricity

《3 薄膜润滑与一般计算轴承特性比较》

3 薄膜润滑与一般计算轴承特性比较

为了更明显地说明偏心率和无量纲吸附层厚度对轴承特性的影响,特采用比值方式进行比较,如图8至图11所示。

图8和图9分别为ε=0.2和ε=0.7时,不同无量纲吸附层厚度下压力比p/p₀^*的变化规律,p₀^*为2σ*=0时的无量纲压力,即常规计算压力。

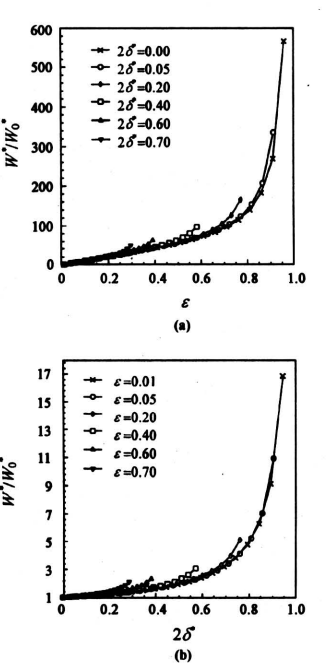
在图10a和图11a中的“₀^*“是在ε=0.01的值时随无量纲厚度2σ*而变化;在图10b和图11b中的ε是在2σ*=0的值时随偏心率e而变化。图10为承载能力比W^*/W₀^*的变化规律,图10a是在不同的吸附层厚度2σ*下, W^*/W₀^*随偏心率的变化;图10b为不同偏心率ε下,W^*/W₀^*随2σ*的变化规律。从图10中可以看出, W^*/W₀^*均随2σ*和ε的增大而增大。

《图7》

图7 无量纲摩擦阻力F^*与2σ*和ε的变化规律

Fig.7 The non-dimensional friction of the bearing as a function of (a) the adsorbed layer thickness and (b) the eccentricity

《图8》

图8 ε=0.2时p/p₀^*的变化规律

Fig.8 The pressure radio p/p₀^* at ε=0.2

《图9》

图9 ε=0.7时p/p₀^*的变化规律

Fig.9 The pressure radio p/p₀^* at ε=0.7

《图10》

图10 承载能力比W^*/W₀^*的变化规律

Fig.10 The load capacity ratio W^*/W₀^*of the bearing as a function of (a) the eccentricity and (b) the adsorbed layer thickness

图11为摩擦阻力比F^*/F₀^*的变化曲线。摩擦阻力反映了摩擦损耗功率。

《图11》

图11 摩擦阻力比F^*/F₀^*的变化规律

Fig.11 The friction ratioF“/F of the bearing as a function of (a) the eccentricity and (b) the adsorbed layer thickness

《4 结论》

4 结论

采用等效粘度修正雷诺方程来求解分子级薄膜润滑径向轴承问题,可以得到精确解。从分析中可知,薄膜润滑壁面效应对径向滑动轴承特性的影响是十分显著的,正是这一影响,使薄膜润滑成为可能,并可能得到新型的润滑剂,只要定时涂抹即可达到薄膜润滑,保证径向滑动轴承不产生磨损。

薄膜润滑由于承载能力提高,在低速下仍能保持油膜润滑,大大改善了轻承的工作性能。若考虑温度的影响,文中的计算值还要进一步修正。一舫来说,油膜厚度的减小将使温度增加,从而可能导致润滑剂特性产生大的改变。所以,所提出的薄膜润滑理论计算公式主要适用于温度变化较小的场合。

从课题研究中得到的启示:如若存在超能吸附,表面将形成强的吸附膜,以保证不产生磨损问题。

展示更多