关于柔性航天器动力学模型降阶问题

摘要

基于变量变换级数展开法，获得了掩埋矩形光波导及脊形光波导的矢量本征模及其传播常数。变量变换使无限平面映射成单位平面，从而使单位平面边界上的电磁场自然为零，消除了非物理反射，提高了计算精度；另外，由于这种方法所导致的矩阵阶数小，因此计算效率较高。分析的结果与已发表的结果吻合较好，可以为优化波导光电子器件的结构提供参考。

正文

《1 引言》

1 引言

为了进行航天器控制设计和动力学仿真, 必须建立柔性航天器动力学模型。这样的模型既应真实反映航天器系统的动力学特性, 其阶数又应足够低, 以便实现所设计的控制策略。同时, 从动力学仿真角度讲, 为提高动力学仿真的计算效率, 模型的阶数也不应太高。因此存在动力学模型的降阶问题。模型降阶可从两方面考虑:一方面是根据经典的假设模态法, 选择具有较好展开收敛性的模态集, 利用这样的模态集代替有限元节点位移表示结构变形, 即进行模态变换;另一方面是提供合适的准则, 以便在模态集中选择合适的保留模态。

《2 常用模态集》

2 常用模态集

柔性航天器可典型地看成由中心体和若干柔性附件组成:中心体可为刚体、柔性体或两者的组合;附件铰接于中心体, 相对于中心体可作缓慢转动。为了将航天器的整体运动 (刚体运动) 与变形运动区分开, 使它们明确反映在所建立的动力学模型中, 采用了通常的混合坐标法的处理方法, 引入固连于中心体局部的中心体固连坐标系。此坐标系的运动反映了航天器的刚体运动, 而航天器结构相对此坐标系的运动反映其变形运动。在航天器附件与中心体的连接点处建立固连于该处附件局部的附件固连系, 该坐标系相对于中心体固连坐标系的运动反映了附件的刚体运动, 而附件结构相对此坐标系的运动反映其变形运动。

按假设模态法的理论, 将变形用模态展开表示。记中心体和柔性附件的变形位移的模态展开表示分别为

$u_{c} = Φ_{c} η_{c}, u_{i} = Φ_{i} η_{i}$ $u_{c} = Φ_{c} η_{c}, u_{i} = Φ_{i} η_{i}$

式中Φ_c和Φ_i分别为相应于中心体变形和附件变形的模态矩阵 (模态集) , η_c和η_i为相应的模态坐标。模态集的选取就是要选择合适的Φ_c和Φ_i, 以便用较少的项表示变形。常用的模态集有四种。

《2.1 部件弹性正则模态集》

2.1 部件弹性正则模态集

选用中心体和附件弹性变形的正则模态表示它们的变形, 这可看成是对通常混合坐标法的推广。应注意所采用的正则模态是相应于有关连体坐标系的。经过适当的步骤, 可得到航天器的动力学方程。由于中心体和附件变形均是相对于相应的附体系而言的, 因而动力学方程中所用的中心体弹性模态为其自由界面正则模态, 而附件弹性模态为固定界面正则模态。为了保证所得到的动力学模型足以反映航天器的动力学特性, 所取的弹性正则模态应足够多。对于中心体柔性较大、附件较大的航天器, 单纯采用部件弹性正则模态集有时不能很好地表示变形。

《2.2 Craig–Bampton (C-B) 模态集 [1]》

2.2 Craig–Bampton (C-B) 模态集 [1]

C-B 模态集由部件的固定界面正则模态和对于界面坐标的约束模态组成。解特征值问题可得固定界面保留正则模态阵, 它的各列由若干个保留的正则模态组成。

对于界面坐标的约束模态是被约束的界面自由度释放时形成的静模态, 其定义为当界面自由度依次为单位位移, 而其他界面自由度位移强制为零时, 由此产生的一系列静态位移。

采用 Craig-Bampton 模态集, 由通常的动力学综合步骤可导出航天器动力学方程。显然, 方程中除包含弹性正则模态坐标外, 还包含界面约束模态坐标。由于在结构变形中引入对于界面坐标的约束模态以计及高阶弹性模态的影响, 因而可采用较少的弹性模态, 且提高了建模精度。但由于在动力学方程中出现约束模态坐标, 因而动力学方程的阶数较高。

《2.3 MacNeal-Rubin (M-R) 模态集 [2,3]》

2.3 MacNeal-Rubin (M-R) 模态集 [2,3]

M-R 模态集由自由界面正则模态和剩余模态组成。自由界面正则模态阵的各列由保留的若干个正则模态组成。

剩余模态是用来弥补略去的高阶模态的。它定义为依次作用单位力于部件的界面自由度上得到的相应于被略去的高阶弹性模态的一系列静位移。

采用自由界面模态综合法, 可导出航天器的动力学方程。应注意这时由于要满足部件间界面协调条件, 剩余模态坐标和弹性正则模态坐标是不相独立的, 因而方程中表示变形的坐标只有弹性正则模态坐标。与采用Craig-Bampton模态集相比, 采用MacNeal-Rubin模态集时, 系统方程中只需用部件的保留弹性正则模态坐标描述结构变形, 因而得到的动力学方程的阶数较低。同时, 采用MacNeal-Rubin模态集进行模态展开具有很好的收敛性, 使所导出的动力学方程较好地反映了航天器的动力学特性。

《2.4 系统结构弹性变形模态集》

2.4 系统结构弹性变形模态集

采用航天器相对于中心体固定坐标系的系统结构弹性变形模态, 也可建立其动力学模型。与采用部件弹性模态建模相比, 动力学方程中只需用系统结构变形模态坐标表示变形, 且模态展开的收敛性较好, 因而方程的阶数明显较低, 建模精度较高。具体建模时仍可从部件模态出发, 通过模态综合得到系统弹性模态。采用部件弹性模态或系统结构变形弹性模态建模的优点是建模过程比较简单, 只需利用部件或系统结构的弹性变形模态和质量矩阵就可建立航天器的动力学方程, 因而较便于应用。

《3 保留模态的选取》

3 保留模态的选取

为了进一步降低动力学模型的阶数, 应在模型中去掉一些模态, 剩下的模态称为保留模态。已有一系列选取保留模态的准则。除了频率准则、惯性完备性准则和传递函数准则外, 对大型柔性航天器常采用以下两条准则。

《3.1 模态价值分析 [4]》

3.1 模态价值分析 [4]

模态价值分析 (MCA) 通过计算模态价值, 提供了一种选择保留模态的方法。与其他方法相比, 模态价值分析直接将模态选择与控制目标联系起来, 因而更加合理。设对角化动力学方程为:

$\begin{array}{l} \ddot{ξ} + 2 ξ Ω \dot{ξ} + Ω^{2} ξ = D u ‚ \\ y = C_{1} ξ + C_{2} \dot{ξ} ‚ \end{array} (1)$ $\begin{array}{l} \ddot{ξ} + 2 ξ Ω \dot{ξ} + Ω^{2} ξ = D u ‚ \\ y = C_{1} ξ + C_{2} \dot{ξ} ‚ \end{array} (1)$

式中ξ为模态坐标, ζ为阻尼对角阵, Ω为模态频率对角阵, u和y分别为输入和输出变量。考虑开环的情况, 这时控制目标函数为:

$V = E \int_{0}^{\infty} y^{Τ} Q y d t ‚$ $V = E \int_{0}^{\infty} y^{Τ} Q y d t ‚$

式中E为期望算子, Q为反映y各分量重要性的一个矩阵。

考虑N个模态, 有

$\begin{array}{l} C_{1} = [c_{11} \dots c_{1 Ν}] ‚ \\ C_{2} = [c_{21} \dots c_{2 Ν}] ‚ \end{array} (2)$ $\begin{array}{l} C_{1} = [c_{11} \dots c_{1 Ν}] ‚ \\ C_{2} = [c_{21} \dots c_{2 Ν}] ‚ \end{array} (2)$

业已证明 ^[5], 在弱阻尼的条件下, 有

$V = \sum_{i = 1}^{Ν} V_{i} ‚$ $V = \sum_{i = 1}^{Ν} V_{i} ‚$

式中V_i 表示第i个模态的模态价值, 且有

$V_{i} = \frac{(c_{1 i}^{Τ} Q c_{1 i} + ω_{i}^{2} c_{2 i}^{Τ} Q c_{2 i}) σ_{i}^{2}}{4 ζ_{i} ω_{i}^{3}} ‚ (3)$ $V_{i} = \frac{(c_{1 i}^{Τ} Q c_{1 i} + ω_{i}^{2} c_{2 i}^{Τ} Q c_{2 i}) σ_{i}^{2}}{4 ζ_{i} ω_{i}^{3}} ‚ (3)$

式中ω和ζ_i分别为第i个模态频率和模态阻尼比, 为σ $_{i}^{2}$ $_{i}^{2}$ 第i个模态广义力的强度 (当考虑受白噪声激励时) , 或第 i个模态坐标的初始速率的均方值 (当考虑初始速度扰动时) 。由式 (3) 可知, 刚体模态的模态价值为无穷大, 显然应该保留。

可以按模态价值的大小对模态进行排列, 保留那些价值高的模态, 略去那些价值很小的模态。一般讲, 模态价值并不按频率大小排列。若模态价值分析要求保留的模态数太多, 则应修改控制目标, 保留合理的模态数。一般讲, 保留模态的选择是个反复的过程。

《3.2 内平衡降阶 [6]》

3.2 内平衡降阶 [6]

内平衡降阶并不是在通常的模态空间内降阶, 而是在经过线性变换后的内平衡空间内进行降阶, 从而解决当模态密集时存在的降阶困难。为进行内平衡降阶, 采用对角化动力学方程 (1) , 并设保留p阶模态, 将方程写成状态方程形式为:

$\begin{array}{l} \dot{χ} = A χ + B u ‚ \\ y = C χ ‚ \end{array}$ $\begin{array}{l} \dot{χ} = A χ + B u ‚ \\ y = C χ ‚ \end{array}$

式中:

$\begin{array}{l} χ = [ξ^{Τ} \dot{ξ}^{Τ}]^{Τ} \\ A = [\begin{matrix} 0 & Ι \\ - Ω^{2} & - 2 ζ Ω \end{matrix}], B = [\begin{array}{l} 0 \\ D \end{array}] ‚ C = [C_{1} C_{2}] \end{array}$ $\begin{array}{l} χ = [ξ^{Τ} \dot{ξ}^{Τ}]^{Τ} \\ A = [\begin{matrix} 0 & Ι \\ - Ω^{2} & - 2 ζ Ω \end{matrix}], B = [\begin{array}{l} 0 \\ D \end{array}] ‚ C = [C_{1} C_{2}] \end{array}$

上面方程中已除去了刚体模态, 因而矩阵A的所有特征值均具有负实部。

所谓内平衡模型是指其能控和能观 Gramian 阵W和V相等, 且已对角化:

$W = V = Σ = d i a g {σ_{i}, i = 1, \dots, 2 p} 。$ $W = V = Σ = d i a g {σ_{i}, i = 1, \dots, 2 p} 。$

这里能控和能观Gramian 阵的定义为:

$W = \int_{0}^{\infty} e^{A t} B B^{Τ} e^{A^{Τ_{t}}} d t, V = \int_{0}^{\infty} e^{A^{Τ_{t}}} C^{Τ} C e^{A t} d t ‚$ $W = \int_{0}^{\infty} e^{A t} B B^{Τ} e^{A^{Τ_{t}}} d t, V = \int_{0}^{\infty} e^{A^{Τ_{t}}} C^{Τ} C e^{A t} d t ‚$

它们为由以下的Lyapunov 方程算得:

$\begin{array}{l} A W + W A^{Τ} + B B^{Τ} = 0 ‚ \\ V A + A^{Τ} V + C^{Τ} C = 0 ‚ \end{array}$ $\begin{array}{l} A W + W A^{Τ} + B B^{Τ} = 0 ‚ \\ V A + A^{Τ} V + C^{Τ} C = 0 ‚ \end{array}$

业已证明 ^[6], 所有线性时不变的渐近稳定模型都可通过线性变换化成平衡形式。而平衡降阶是先将模型化成平衡形式, 然后对平衡状态进行截断。截断的依据为对角化Gramian阵中的标量σ_i的大小。相应于小σ_i的平衡状态对于输入u较不可控, 对于输出y较不可观, 因而这些状态可以截去。标量σ_i在状态变换下不变, 且等于Gramian阵乘积的特征值的方根:

$σ_{i} = \sqrt{λ_{i} W V} 。$ $σ_{i} = \sqrt{λ_{i} W V} 。$

因而, 就模型降阶而言, 并不一定要将模型化为平衡形式, 只要将Gramian阵乘积对角化就可。

平衡模型降阶的一个重要性质是存在以下的∞范数频率误差边界:

$| G^{2 p} (j ω) - G^{k} (j ω) |_{\infty} \leq 2 \sum_{i = k + 1}^{2 p} σ_{i}, k < 2 p$ $| G^{2 p} (j ω) - G^{k} (j ω) |_{\infty} \leq 2 \sum_{i = k + 1}^{2 p} σ_{i}, k < 2 p$

式中G^2p (s) =C[sI-A]^-1B为全阶模型的传递矩阵, G^k (s) 为截断后的k阶模型的传递矩阵。传递矩阵可写成各弹性模态部分之和:

$G^{2 p} (s) = \sum_{i = 1}^{\infty} G_{i}^{2 p} (s), G_{i}^{2 p} (s) = \frac{(c_{1 i} + c_{2 i} s) d_{i}}{s^{2} + 2 ζ_{i} ω_{i} s + ω_{i}^{2}}$ $G^{2 p} (s) = \sum_{i = 1}^{\infty} G_{i}^{2 p} (s), G_{i}^{2 p} (s) = \frac{(c_{1 i} + c_{2 i} s) d_{i}}{s^{2} + 2 ζ_{i} ω_{i} s + ω_{i}^{2}}$

式中ζ_i, ω_i分别是对角阵ζ, Ω的第i个元素, d_i是D的第i行, c_1i, c_2i分别是C₁, C₂的第i列。

Gregory证明 ^[7], 具有分离频率的小阻尼结构的模态模型近似为平衡的, 此外, 他还得到了计算标量σ_i的近似表达式为:

$\begin{array}{l} σ_{i} \approx \frac{\sqrt{b_{i} b_{i}^{Τ} (c_{1 i}^{Τ} c_{1 i} + ω_{i}^{2} c_{2 i}^{Τ} c_{2 i})}}{4 ζ_{i} ω_{i}^{2}} \\ σ_{p + i} \approx σ_{i}, i = 1, \dots, p \end{array} (4)$ $\begin{array}{l} σ_{i} \approx \frac{\sqrt{b_{i} b_{i}^{Τ} (c_{1 i}^{Τ} c_{1 i} + ω_{i}^{2} c_{2 i}^{Τ} c_{2 i})}}{4 ζ_{i} ω_{i}^{2}} \\ σ_{p + i} \approx σ_{i}, i = 1, \dots, p \end{array} (4)$

按平衡降阶思想, 具有小σ_i的模态较不受作用力的影响, 并对输出的贡献较小。由于σ_i表示模态的影响程度, 因而可称为模态影响系数。

模态频率的分离程度可按以下准则判断:

$\frac{\max (ζ_{i}, ζ_{j}) \max (ω_{i}, ω_{j})}{| ω_{i} - ω_{j} |} ≪ 1, i \neq j (5)$ $\frac{\max (ζ_{i}, ζ_{j}) \max (ω_{i}, ω_{j})}{| ω_{i} - ω_{j} |} ≪ 1, i \neq j (5)$

若满足式 (5) , 则说频率ω_i, ω_j足够分开, 但大部分空间结构呈现频率密集成团的状况, 上述准则将不被满足。这时一般的经验是不管上述准则方程, 仍按Gregory提供的近似表达式计算各模态的σ_i并按其大小进行模态选取;或者可以将不满足准则方程的那些模态集结成组, 对每个密集模态组进行分析以确定是否需保留具有小模态影响系数的模态 ^[8]。在这种情况下, 将保留所有具有大的σ_i的模态和一些具有小的σ_i的模态。可采用前面的误差边界方程来确定应保留多少模态。

《4 降阶策略和算例》

4 降阶策略和算例

模态价值分析准则是针对航天器系统模态的降阶准则, 内平衡法是在内平衡空间内降阶, 即使对于具有分离频率的小阻尼结构, 它也是针对系统模态的降阶。而航天器动力学建模时的降阶要求对于部件弹性模态降阶, 即使采用系统弹性模态建模, 也是针对相对于附体系的弹性变形模态的降阶。因而存在如何将模态价值分析准则和内平衡准则用于动力学建模时降阶的问题。为此提出以下策略:

1) 采用试算法, 逐步增加所用的弹性模态数, 建立航天器系统的动力学方程。对得到的动力学方程进行特征值分析, 得到航天器系统模态特征值。当足够多阶特征值与系统有限元分析结果 (或理论结果) 一致时, 表明得到的动力学模型已较精确。

2) 计算相应动力学方程特征模态的模态价值和内平衡模态影响系数, 确定应保留的航天器系统模态 (系统保留模态) 。

3) 选用不同数结构弹性模态, 建立系统的动力学方程, 解动力学方程的特征值问题, 得到系统模态。将采用不同数结构弹性模态建模时得到的系统模态特征频率和有限元分析结果进行比较, 选用对于系统保留模态能确保得到较精确结果的最少结构弹性模态数。

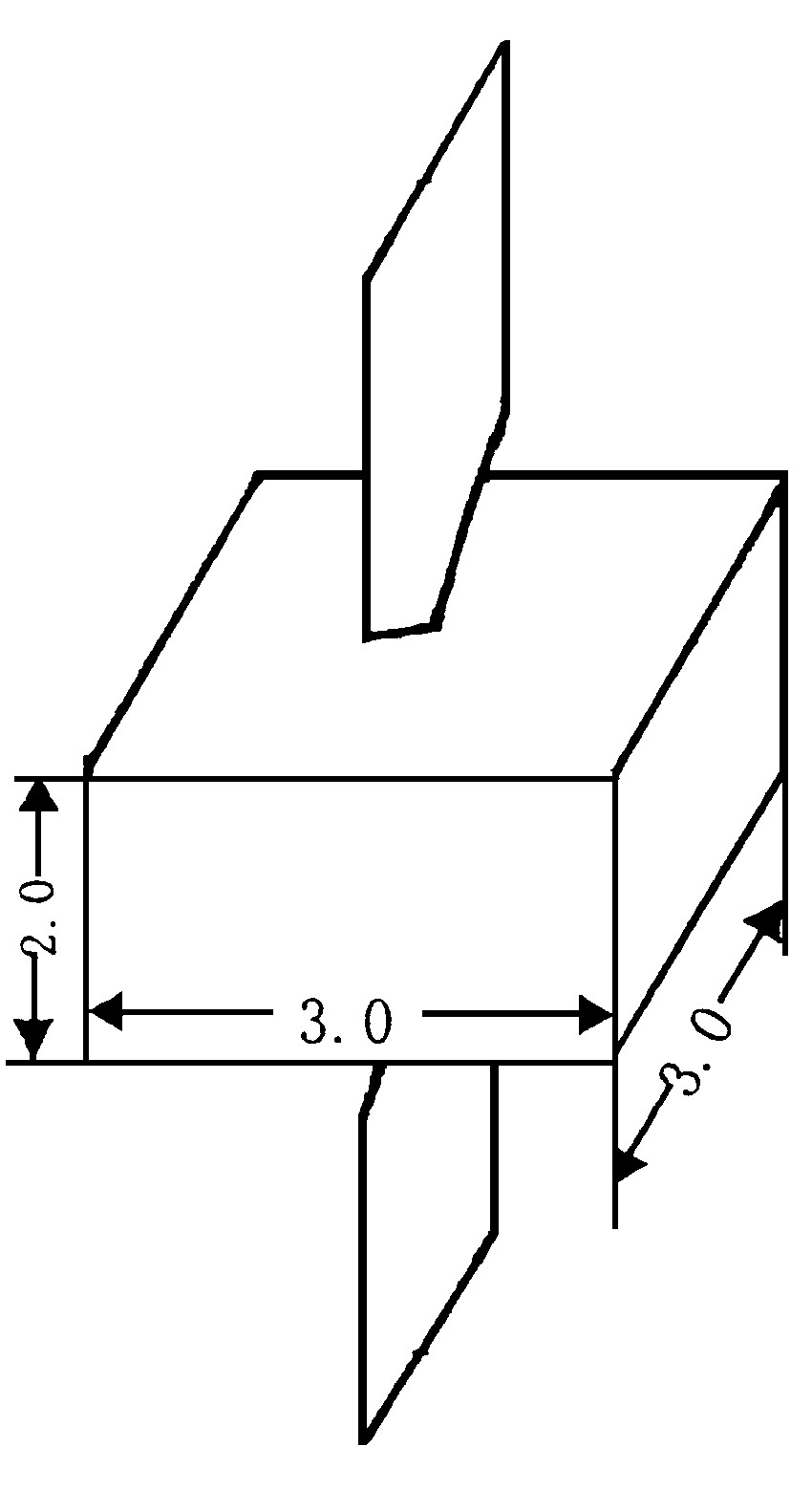
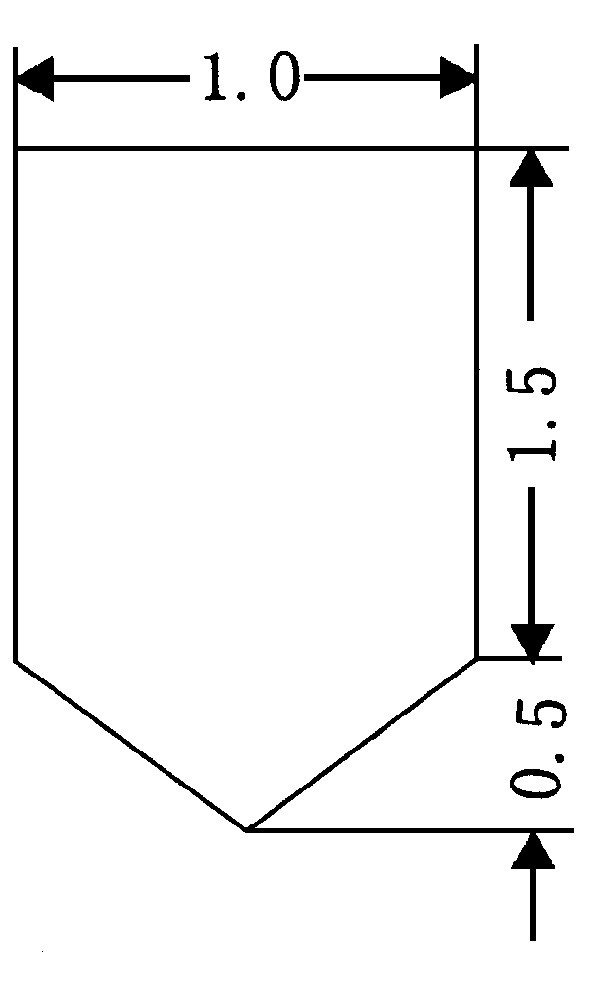
考虑由盒形中心体和两块帆板组成的柔性航天器系统, 如图1所示。中心体盒尺寸为2 m × 3 m × 3 m, 其面板厚0.001 5 m, 材料为铝。两块帆板的材料也为铝, 尺寸见图2, 厚度为0.001 5 m。

采用部件模态集、Craig-Bampton模态集和由模态综合法得到的系统结构弹性变形模态集建模, 对各自所导出的动力学方程进行特征值分析, 得到的自由系统的特征频率除包含六个零频率外, 非零频率的比较见表1。

《图1》

图1 盒—板系统的位形

Fig.1 Configuration of the box-plane system

《图2》

图2 帆板尺寸

Fig.2 Drawing of the solar array

表1 由动力学方程得到的特征频率与有限元分析结果的比较

Table 1 Eigenfrequencies from dynamics equations compared with the FEM values

《表1》

阶数		特征频率/Hz
阶数		1	2	3	4	5	6
	部件弹性模态集	0.76	0.81	1.52	1.89	2.16	2.35
动力学方程解	Craig-Bampton 模态集	0.59	0.64	1.80	2.36	2.36	2.43
	系统弹性变形模态集	0.54	0.58	1.83	2.37	2.38	2.45
有限元分析结果		0.55	0.55	2.32	2.37	2.65	2.65

由表1可见, 采用部件模态建模时的值与有限元分析结果相比, 其误差较大, 尽管此时中心体取了12阶模态, 而每个帆板取了8阶模态。这是由于此时采用部件弹性模态已不能很好表示航天器结构变形的缘故。采用Craig-Bampton 模态集时由于引入了静变形模态, 使导出的动力学模型的精度提高了, 因而由其得到的系统特征频率已接近有限元分析的结果。采用相对于中心体固连系的系统结构弹性变形模态建模, 当取20阶模态时, 由相应的动力学方程得到的系统固有频率较接近有限元分析的结果, 表明这样的模态集可得到较高的模型精度, 且这时所取的模态阶数已足够多。

以航天器的三个转角为输出, 相应的转矩为输入, 计算采用20阶系统结构弹性变形模态建模时动力学模型的各阶非零模态的模态价值和内平衡模态影响系数, 所得结果见表2。

表2 模态价值和内平衡模态影响系数

Table 2 Modal costs and modal influence coefficients

《表2》

模态序号	1	2	3	4	5
模态价值	0.124 ×10^-7	0.476 ×10^-5	0.810 ×10^-13	0.486 ×10^-11	0.377 ×10^-11
模态影响系数	0.154 ×10^-3	0.935 ×10^-2	0.391 ×10^-6	0.234 ×10^-5	0.205 ×10^-5

由表2可看出, 对于目前的输出和输入, 从模态价值分析和内平衡准则的角度看, 系统的前两阶模态起决定作用, 其他模态的模态价值或模态影响系数比它们小得多, 即相对头两阶模态讲, 其他模态对控制目标的贡献很小, 它们较不能控, 也较不能观。因此, 对此航天器系统, 从控制角度讲, 只需保留头两阶系统模态。而由表 1 可知, 由采用系统结构弹性变形模态建立的动力学方程得到的头两阶系统模态特征频率很接近有限元分析的结果。因此, 对本例讲, 采用20阶系统结构弹性变形模态建立的动力学模型已足够准确, 它可保证由其得到的头两阶系统模态足够精确。

展示更多