《1 前言》
1 前言
网络流中断问题是一类经典的网络流优化问题,对此类问题的相关研究起源于 19 世纪 60 年代[1,2] 。此问题可以视为Stackelberg [3] 博弈的特殊情况,模型中有两个局中人分别成为中断者和入侵者,中断者先选择中断策略抵御入侵者,中断策略一般为在某些边上设置中断点或者监测装置,其目的是在有限资源下尽可能减少入侵者带来的伤害。Steinrauf等 [4] 利用网络流中断模型研究了在城市之间如何设置关卡来防止毒品进入一些大城市。Wood [5] 证明了此问题属于NP-完全(non-deter-ministic polynomial completeness)问题,之后的研究大多从启发式算法的角度解决此问题 [6~9] 。Wood [5]又将网络流中断问题化为整数规划问题并给出了两个有效的不等式来缩小解空间。事实上,CPLEX是IBM(International Business Machines Corporation)研发的一款可以求解整数规划问题的软件,可以解决较大规模的整数规划问题。而在实际应用中,入侵者突破已设置中断点的情况也很常见,这促使目前对网络流中断问题的研究加入了随机性,即中断者在边上设置中断点时需要考虑对此边中断不一定成功。Cormican等 [10] 提出了随机网络流中断模型并设计了相应的近似算法。Berry等 [11] 将随机网络流中断模型应用于市区水网的检测问题中,在其研究中将检测器放置在管道中,检测器通过水的特征(如水温、氯含量、颜色、传导性和pH等)来检测水中是否有毒,这种检测手段不是100 %正确的。随着“9.11事件”的发生此类模型有了新的应用方向,比如国土安全(homeland security)[12] 、关键设施和关键资源(critical infrastructure and key resources,CI-KR) [13] 以及其他涉及恐怖袭击事件的领域。Morton等 [14] 从国土安全的角度将网络流中断问题用于核走私的研究中,文中通过在可能的运输路径上设置放射检测器来最小化走私者走私成功的概率。结合关键设施保护的应用,Scaparra等 [15] 以网络流中断问题为基础建立了双层整数规划模型并给出了隐含枚举(implicit enumeration)算法,此算法实际上和枚举算法相差甚少。事实上,大部分中断问题都可以转化为双层整数规划问题 [15,16] 。目前对于双层整数规划问题的研究没有实质性的突破。双层整数规划问题的难度一般取决于下层规划问题,下层规划问题如果是线性规划问题则此双层整数规划问题可很容易转化成整数规划问题,进而可用CPLEX来解决;下层规划问题如果是线性整数规划问题通常只能采用遍历手段。
考虑到监测点可能失效的情况,本文在网络流中断模型的基础上加入了可靠策略的概念,此概念是指即使某些监测点失效仍然能够达到原有的目的。本文的模型是在给定资源情况下,通过在起点到终点的所有路径设置一定数量的监测点来更好抵御入侵者,这与随机网络流中断模型中将所有监测点设置为相等的成功监测概率相同。事实上可靠性的思想是必要的,假设一个监测点能够成功监测异常情况的概率是80 %(这在很多应用尤其是国土安全等领域是不理想的),则这一异常情况能够被两个监测点监测出的概率为1-(1-80 %)2 =96 %;而被三个监测点监测出的概率为 1-(1-80 %)3 =99.2 %。我们的模型是在有限的资源下,选择一些边设置监测点使得从起点到终点的所有路径包含尽可能多的已被监测的边,即最大化所有路径包含已监测边数量的最小值。此研究不仅可直接应用于一些其他的网络中断模型中,如边境防御、CIKR、水资源监测等,同时也提供了一种解决双层整数规划模型的方法。
《2 模型》
2 模型
G (N,D,s,t,a,R ) 表示以 N 为顶点集, D 为边集, s 为起点, t 为终点的有向图,其中函数 表示在边
表示在边 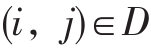 上设置监测点所需的花费
上设置监测点所需的花费  , R 表示中断者的资源限制。此模型是指在给定资源限制 R 下,即使入侵者能够通过中断者在某些边上所设置的监测点,仍然不能从起点 s 到达终点 t ,即最大化从 s 到 t 的所有路径中包含监测点的边的数量的最小值。模型有下面的线性整数规划形式:
, R 表示中断者的资源限制。此模型是指在给定资源限制 R 下,即使入侵者能够通过中断者在某些边上所设置的监测点,仍然不能从起点 s 到达终点 t ,即最大化从 s 到 t 的所有路径中包含监测点的边的数量的最小值。模型有下面的线性整数规划形式:

式(1)中, ρ 为所有从 s 到 t 的路径; =1 表示在边
=1 表示在边 上设置监测点,否则
上设置监测点,否则  =0 。
=0 。
一般来说,即使图的规模不大,两点之间所有路径的数量也非常大,从计算复杂性角度来说,两点之间所有路径的数量是图的规模的指数次幂。为此将 PATH 模型转化为下面的双层整数规划模型:

式(2)中,f 为给定任意可行  后如下规划问题的最优目标函数值:
后如下规划问题的最优目标函数值:

式(3)中, 表示的意义与在 PATH 模型中相同,边(t,s ) 是终点t 到起点s 的虚拟边;
表示的意义与在 PATH 模型中相同,边(t,s ) 是终点t 到起点s 的虚拟边;  为虚拟边 (t,s )上的虚拟流量;
为虚拟边 (t,s )上的虚拟流量;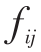 为边
为边  上的流量;
上的流量; =1 为入侵者会破坏边
=1 为入侵者会破坏边  上所设置的监测点,否则
上所设置的监测点,否则  =0 。
=0 。
在给出两个模型等价性的证明之前,需要对资源R 给出一些限制。显然,若资源R 不能够使得在s 到t 的每条路径中至少含有一个带有监测点的边,即 PATH 模型的最优值为0,则 BIP 模型的下层规划问题无可行解。笔者指出这一临界值是很容易判断的。
命 题 1. 令  是 图
是 图 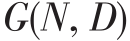 中 边
中 边 的 容 量 限 制 为
的 容 量 限 制 为  的 网 络 图 ,
的 网 络 图 , 是
是 的最大流。则 opt (PATH)≥1 当且仅当R ≥R 1 ,其中 opt (PATH) 是模型 PATH 的最优目标函数值。
的最大流。则 opt (PATH)≥1 当且仅当R ≥R 1 ,其中 opt (PATH) 是模型 PATH 的最优目标函数值。
证明:由于R 1 是  的最大流值,根据最大流最小割定理, R 1 也是
的最大流值,根据最大流最小割定理, R 1 也是  的最小割量。令 x 是
的最小割量。令 x 是  的最小割,即从 s 到 t 的所有路径都包含 x 中的至少一条边,显然 (x,1) 是模型 PATH 的最优解 。 故当 R ≥R 1 时必有opt (PATH)
的最小割,即从 s 到 t 的所有路径都包含 x 中的至少一条边,显然 (x,1) 是模型 PATH 的最优解 。 故当 R ≥R 1 时必有opt (PATH) 1 ,反之亦成立。
1 ,反之亦成立。
综合可得,若R  R 1 ,模型 PATH 无可行解;若R =R 1 , opt(PATH)=1 。下文如无特别说明,约定R
R 1 ,模型 PATH 无可行解;若R =R 1 , opt(PATH)=1 。下文如无特别说明,约定R  R 1 。
R 1 。
命题2. 模型 BIP 等价于模型 PATH ,也即在相同的图中,对于相同的参数 R ,他们有相同的目标函数值。
证明:令 (x,k ) 是模型 PATH 的可行解,需证明(f,x,k ) 也是模型 BIP 的可行解,其中 f=0 ,仅需证明模型 BIP 的上层规划问题中 成立。若其不成立,由于
成立。若其不成立,由于  是 0-1 变量,则存在一条从 s 到 t 的路 P * ,对于所有其上的边都有
是 0-1 变量,则存在一条从 s 到 t 的路 P * ,对于所有其上的边都有  ,但
,但 与
与  矛盾。
矛盾。
反之令(f,x,k )是模型 BIP 的可行解,其中f =0 。由于在上层规划约束中  ,则不存在任何从 s 到 t 的路,由于
,则不存在任何从 s 到 t 的路,由于  可知在任意s 到 t 的路 P*中必有
可知在任意s 到 t 的路 P*中必有  ,从而可得 (x,k )也是模型 PATH 的可行解。
,从而可得 (x,k )也是模型 PATH 的可行解。
下面仅需解决模型 BIP ,如在前言中所示,其下层规划是整数规划,这在一般情况下是无法将双层整数规划模型转化为整数规划模型的,故此需要一些转化手段。
《3 模型求解》
3 模型求解
由于双层整数规划模型的难点在于下层规划,为解决模型 BIP ,首先从下层规划的讨论开始。
《3.1 线性规划松弛》
3.1 线性规划松弛
一个常用的处理整数规划方法就是求解其线性规划松弛。由于在上层规划中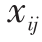 =0,1 并且在下 层 规 划 中
=0,1 并且在下 层 规 划 中  ,我 们 将 用
,我 们 将 用  来 代 替
来 代 替 =0,1 。由此得到如下的下行规划形式:
=0,1 。由此得到如下的下行规划形式:

引理1. opt (IP)∈{0,1}
证明:由于
 1 ,将图 G (N,D ) 的每条边加上流量限制 1 不会对模型 IP 的最优解产生变化。因此如果有一条从 s 到 t 的路流量不为 0 ,则可令这条路上的所有边的流量为 1 ,其余边的流量为 0 即可得到流值为 1 的最优解。否则显然有 opt (IP)=0 。
1 ,将图 G (N,D ) 的每条边加上流量限制 1 不会对模型 IP 的最优解产生变化。因此如果有一条从 s 到 t 的路流量不为 0 ,则可令这条路上的所有边的流量为 1 ,其余边的流量为 0 即可得到流值为 1 的最优解。否则显然有 opt (IP)=0 。
命题3. 设 (f,x,k ) 是模型 BIP 的最优解,则至少存在一条从 s 到 t 的路 P0 满足
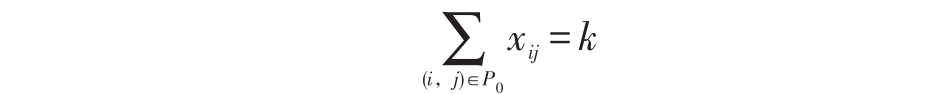
证明:若 (f,x,k ) 是模型 BIP 的最优解,由命题2可知, (x,k ) 是模型 PATH 的最优解,也即 k 是模型 PATH 的最优目标函数值。若对任意从 s 到 t 的路 P* 都有 ,则 (x,k +1) 是模型 PATH的可行解,这与 PATH 的最优目标函数值是 k 相矛盾。
,则 (x,k +1) 是模型 PATH的可行解,这与 PATH 的最优目标函数值是 k 相矛盾。
根据引理1和命题3,我们有如下关于模型 IP和模型 LP 最优值的相关关系式:
定理1. opt (IP)=0⇔opt (LP)=
其中 opt (IP) 是模型 IP 的最优值, opt (LP) 是模型 LP 的最优值。
证明: “⇐” 由 opt (IP) opt (LP) 以及定理1可直接得到。
opt (LP) 以及定理1可直接得到。
“⇒” 将分别构造模型 LP 及其对偶问题的目标值都为 的解。
的解。
由命题3可知,存在一条从 s 到 t 的路 P0 满足 。模型 LP 的对偶有如下形式:
。模型 LP 的对偶有如下形式:

首先构造模型 LP 的可行解。令

则:

模型 LP 中的其余约束条件容易检验,且此可行解对应的目标函数值为 。
。
构造模型 DLP 的可行解如下,设

令 G (N,D,β ) 是图 G (N,D ) 中边 (i,j )∈D 的容量限制为 的网络图,
的网络图,  是图 G (N,D,β ) 中从 s 到 i 的最短路长度。则对于所有的
是图 G (N,D,β ) 中从 s 到 i 的最短路长度。则对于所有的 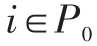 ,
, 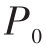 中从 s 到 i 的路一定是图 G (N,D,β ) 中从 s 到 i 的最短路并且
中从 s 到 i 的路一定是图 G (N,D,β ) 中从 s 到 i 的最短路并且 =1 。否则设
=1 。否则设  是
是 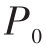 中从 s 到 i 的路,
中从 s 到 i 的路, =
= +
+ 且 P3 是图 G (N,D,β ) 中从 s 到 i 的最短路。则 P3 +P2 是图 G (N,D,β )中从 s 到 t 的路且
且 P3 是图 G (N,D,β ) 中从 s 到 i 的最短路。则 P3 +P2 是图 G (N,D,β )中从 s 到 t 的路且 <1,由此可知
<1,由此可知 ,这与x 的可行性矛盾。
,这与x 的可行性矛盾。
有:
1)若 (i,j )∈D 且 i, ,
,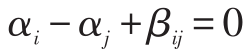 ;
;
2)若(i,j )∈D 且 ,
, 。
。

3)若(i,j )∈D 且 ,
,
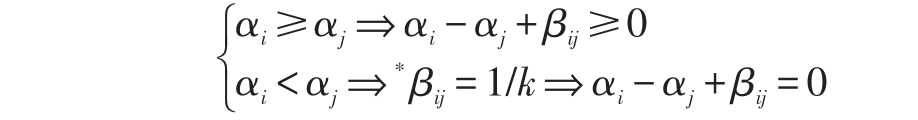
其中 ⇒*是由于若 ,则必有
,则必有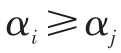
4)若 (i,j )∈D 且 ,
,

模型 DLP 中的其余约束条件可容易检验,且此可行解对应的目标函数值为 。由对偶定理可知,所构造的模型 LP 和模型 DLP 的可行解都是最优解,且最优目标函数值为
。由对偶定理可知,所构造的模型 LP 和模型 DLP 的可行解都是最优解,且最优目标函数值为 。
。
接下来可用对偶方法来处理模型 LP 。
《3.2 线性规划对偶》
3.2 线性规划对偶
在定理1的证明中分别构造了模型 LP 和模型DLP 的最优解,由此可直接得到如下推论:
对任意模型 BIP 的可行解 (f,x,k ) ,若opt (IP)=0 ,则存在一个模型 DLP 的最优解 满 足 :
满 足 : ,
,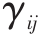 =0 对 任意的(i,j )∈D 成立。
=0 对 任意的(i,j )∈D 成立。
由定理1可知,模型 BIP 的上层规划中的约束  等价于 opt (DLP)=(k-1)/k ,则由推论可知,
等价于 opt (DLP)=(k-1)/k ,则由推论可知,  等价于如下的不等式组有可行解:
等价于如下的不等式组有可行解:

由于当用 (IE1) 代替上层规划中的约束 时
时 都是变量,此时 (IE1) 中的第一个不等式就是未知量的二次形式,需将其转化成一次形式。
都是变量,此时 (IE1) 中的第一个不等式就是未知量的二次形式,需将其转化成一次形式。
《3.3 模型线性化》
3.3 模型线性化
用  代替
代替 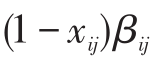 ,并且对于任意 (i,j )∈D 加入如下不等式组:
,并且对于任意 (i,j )∈D 加入如下不等式组:

得到:

定理2. 如果 IE1 有可行解,则 IE2 也有可行解,反之亦然。
证明:令 是 IE1 的可行解,对任意
是 IE1 的可行解,对任意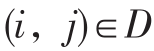 令
令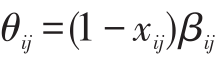 ,则
,则 是 IE2的可行解。
是 IE2的可行解。
反之,令 是 IE2 的可行解,对任意
是 IE2 的可行解,对任意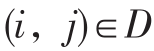 有:
有:

则

因此 是 IE1 的可行解。
是 IE1 的可行解。
令 ,综合以上结论,得到与模型 BIP 等价的如下混合整数规划模型:
,综合以上结论,得到与模型 BIP 等价的如下混合整数规划模型:
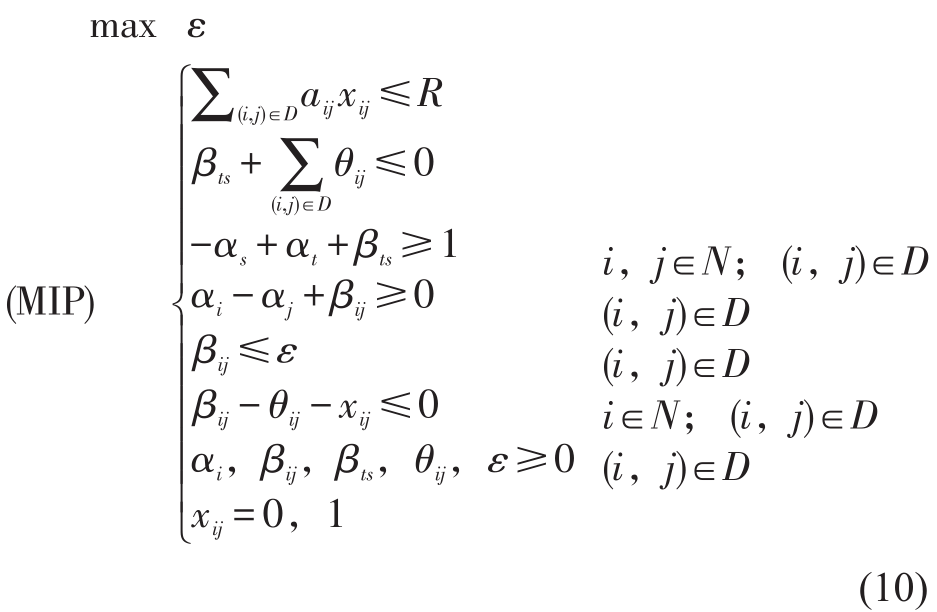
MIP 可由 CPLEX 软件解得 ,完成了从含有图G (N,D ) 的规模的指数次幂数量级个约束的模型PATH 到仅含有与图 G (N,D ) 的规模同阶数量级个约束的模型 MIP 的转化。即:
定理3.对于给定的图 G (N,D ) ,
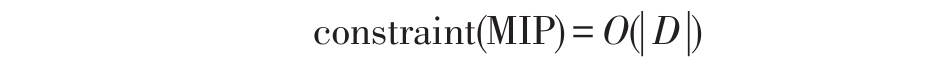
其中 |D | 表示 D 中元素个数, constraint(MIP) 表示模型 M 中约束个数。
《4 模型扩展》
4 模型扩展
本节讨论可靠网络中断模型的两个不同形式。
《4.1 中断点》
4.1 中断点
在以上的讨论中限制了仅能对边设置监测点,本小节考虑在顶点设置监测点的情况。此种情况仅需将每个顶点 ∈N 换成两个顶点
∈N 换成两个顶点  和
和  ,并加上边 (
,并加上边 ( ,
, ) ,并且所有在原图 G (N,D ) 中进入顶点 i的边全部进入顶点
) ,并且所有在原图 G (N,D ) 中进入顶点 i的边全部进入顶点  ,所有在原图G (N,D ) 中离开顶点
,所有在原图G (N,D ) 中离开顶点  的边全部离开
的边全部离开  。在新构造的图中用前述的转换方法可完成模型约束的简化。
。在新构造的图中用前述的转换方法可完成模型约束的简化。
《4.2 多个起点和多个终点》
4.2 多个起点和多个终点
此时仅需设置一个超级起点和超级终点,并将超级起点连接所有原有起点,将所有原有终点连接超级终点,并将在新建的所有边上的中断费用设置足够大即可。
《5 结语》
5 结语
本文考虑了一种新的网络中断模型,鉴于此模型约束条件的复杂性,利用线性规划理论及其他工具对此模型的约束条件进行了极大的简化。在理论上说提供了一个解决双层整数规划模型的方法,从应用上说此模型可直接用于边境控制、国土防御以及水资源监测等领域,具有一定的理论和应用价值。













 京公网安备 11010502051620号
京公网安备 11010502051620号




