钨合金的冲击拉伸行为及其本构和断裂判据的表述

摘要

利用飞轮式Hopkinson拉杆实验技术对钨质量分数为93% 的钨合金在-50～100℃温度范围、应变率ε=10²～10³s^-1区间的动态拉伸性态进行了测试，提供了相应的σ-ε曲线和最大拉伸失效应变，并以此为依据建立了该合金动态拉伸行为的本构关系，提出了该合金受动载发生塑性失稳以致发生拉断的判据。利用断口分形分析理论，对试件拉伸断口微观特征所作的分析和对宏观力学性态实验所作的结论给予了有力的支持。

正文

《1 前言》

1 前言

钨质量分数为93%的锡合金(以下简称钨合金)由于其良好的强度和韧性、高的密度而成为军事上非常令人关注的材料。它在冲击载荷作用下动态力学性能和动态断裂失效机制多年来一直是国内外学者研究的重要课题^[1~4]。锻造态钨合金作为各种反装甲穿甲弹的主体材料,其在火炮膛内发射时所遭受的膛压高达500一600MPa,惯性加速度达(40000一60000) X g,火药燃烧温度高达数千度。在此冲击加载的条件下,弹体材料内将会形成高于膛压1倍以上的瞬态应力、高达10²~10³s^-1的应变率以及百度量级的瞬间升温。特别是弹体的尾部,由于遭受很强的惯性后座力而形成很高的瞬态拉伸应力,从而可能造成尾部断弹现象。因此,实验分析该种钨合金的冲击拉伸特性及其断裂机制具有重要的实际意义。

笔者对钨合金在应变率高达10²~10³s^-1范图内的动态拉伸性态、最大拉伸失效应变进行了直接测量,建立了描述其动态拉伸行为的本构模型,提出了材料发生塑性失稳以致发生拉伸断裂的判据。此外,对动态拉伸断口微观特征所作的分形分析,从微观上对材料的宏观动态拉伸特性提供了依据和支持。

《2 实验技术与结果》

2 实验技术与结果

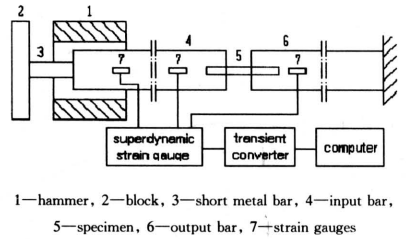
图1展示的是用来对材料进行动态拉伸实验的装置示意图,受检测的材料试件的几何构形及其与Hopkinson拉杆输入与输出杆的连接方法如图2所示。该动态拉伸实验装置由一个直径为1.4m、转动线速度可以达到100m/s的飞轮和一骜Hopkinson杆系统组成。靠近飞轮外缘某处装有受控弹出的两片锤头。当飞轮边缘的线速度达到预先设定的数值时,2片锤头1(见图1)瞬间被弹出并以该速度撞击金属块2,此时,与它及输入杆4相连接的LY~12铝合金短杆3被拉断,于是一个近似方波的拉伸应力脉冲经过输入杆4传入受测试件5。当拉伸脉冲传至试件与输出杆6分界面时发生反射,形成反射波传入试件及输入杆中,同时有一透射波传人输出杆中。这些波利用粘贴在2个杆子上的应变传感器~动态应变仪系统记录下来。并借助于如下公式算出试件所受到的平均拉伸应力σ_s、拉伸应变ε_s及平均应变率ε_s,即

\(\sigma_{\mathrm{S}}(t)=\frac{E A_{0}}{2 A_{\mathrm{S}}}\left[\varepsilon_{\mathrm{i}}(t)+\varepsilon_{\mathrm{r}}(t)+\varepsilon_{\mathrm{T}}(t)\right]=E \frac{A}{A_{0}} \varepsilon_{\mathrm{T}}\), (1)

\(\begin{aligned} \varepsilon_{\mathrm{S}}(t)=& \frac{C_{0}}{L_{\mathrm{S}}} \int_{t_{1}}^{t}\left[\varepsilon_{\mathrm{i}}(t)-\varepsilon_{\mathrm{r}}(t)-\varepsilon_{\mathrm{T}}(t)\right] \mathrm{d} \tau=\\ & \frac{2 C_{0}}{L_{0}} \int_{t_{1}}^{t}\left[\varepsilon_{\mathrm{i}}(t)-\varepsilon_{\mathrm{T}}(t)\right] \mathrm{d} \tau \end{aligned}\) , (2)

\(\varepsilon_{\mathrm{S}}(t)=\frac{C_{0}}{L_{\mathrm{S}}}\left[\varepsilon_{\mathrm{i}}(t)-\varepsilon_{\mathrm{r}}(t)-\varepsilon_{\mathrm{t}}(t)\right]=\\ \frac{2 C_{0}}{L_{\mathrm{S}}}\left[\varepsilon_{\mathrm{i}}(t)-\varepsilon_{\mathrm{T}}(t)\right]\) 。（3）

其中E,A₀,C₀分别为两杆的杨氏模量、截面积及弹性波速;L_s,A_s分别为受拉伸试件的长度及截面积;下标i,r,T分别表示入射波、反射波及透射波。

《图1》

图1 动态拉伸实验装置示意图

Fig.1 The sketch of experimental setup for the shock tension of material

《图2》

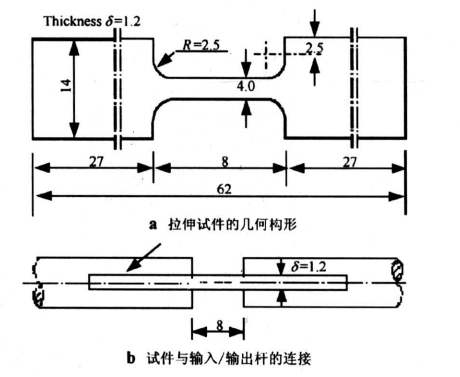
图2 拉伸试件的几何构形及其与输入/输出杆的连接

Fig.2 The geometry of the testing specimen and the connection method of the specimen with the input bar and output bar

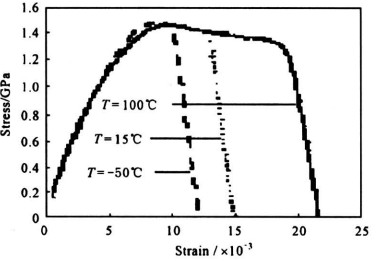
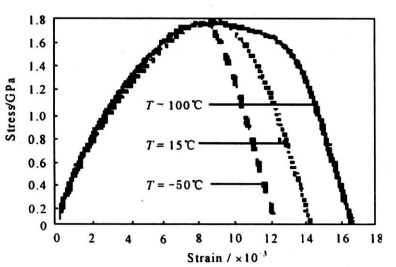
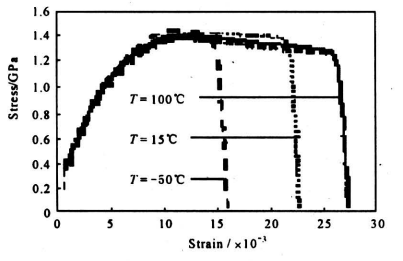
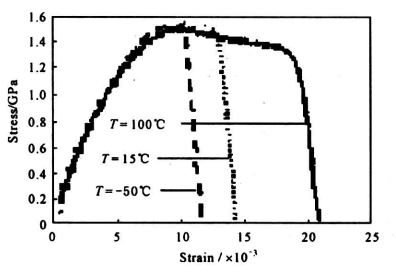
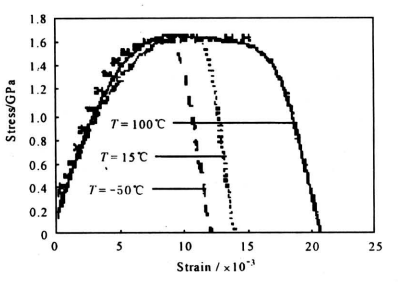
为了检测温度对材料动力学性能的影响,在两杆中间部位安装了保温箱,采用电热技术及液氮冷冻方法对检测试件进行加热或冷冻。实验中选用了-50℃,15℃(室温),100℃三种温度条件。图3、图4和图5给出了实验得到的钨合金在上述环境温度下不同应变率时的动态拉伸应力一应变曲线。图6、图7和图8、图9给出了同一应变率时不同温度条件下实测到的σ-ε曲线。表1展示的是钨合金动态拉伸屈服限及材料塑性失稳应变ε₁随温度及应变率变化。从这些实验曲线和数据可以看出:a.该钨合金材料表现出了非常明显的应变率敏感性,它们在动态拉伸时的屈服限随着应变率的提高而提高。例如在室温条件下,其在ε=1300s^-1时的动态拉伸屈服限比其静态值提高了约45%。这里需要指出,该合金在拉伸变形的初期阶段的σ-ε曲线显示了弧形上升的响应形态,这种非线性粘弹性变形特性用多种观测技术都曾检测到过。这种情况使得动态屈服点变得难以确认。表1所列的数据,是用σ_0.2的原理确定的。b.在相同环境温度下,材料塑性失稳的最大应变ε₁是随着应变率的提高而减小的。例如,15℃,ε=1300s^-1的ε₁值约为2.08%,而当应变率ε提高到1300s^-1时,其最大塑性失稳应变却减小到了0.98%,减小量达50.34%。c. 温度对该合金动态拉伸特性的影响主要不是表现在动态屈服限的改变上,而是表现在最大塑性失稳应变ε₁的数值上。例如,在ε=100s^-1时,-50℃时ε₁的值为1.36%,而在15℃和100℃时ε₁却分别提高到2.08%和2.42%。这表明,材料的塑性随着温度的上升明显地变好了。

《图3》

图3 -50℃下的σ-ε曲线

Fig.3 The σ-ε curves at T= -50℃

《图4》

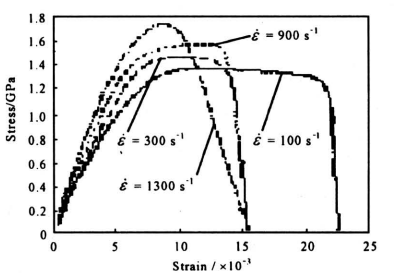
图4 15℃下的σ-ε曲线

Fig.4 The σ-ε curves at T=15℃

《图5》

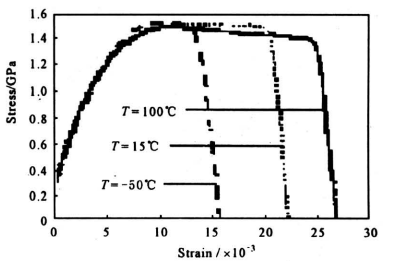
图5 100℃下的σ-ε曲线

Fig.5 The σ-ε curves at T=100℃

《图6》

图6 在ε=100s^-1下的σ-ε曲线

Fig.6 The σ-ε curves at ε=100s^-1

《图7》

图7 在ε=300s^-1下的σ-ε曲线

Fig.7 The σ-ε curves at ε=300s^-1

《图8》

图8 在ε=900s^-1下的σ-ε曲线

Fig.8 The σ-ε curves at ε=900s^-1

《图9》

图9 在ε=1300s^-1下的σ-ε曲线

Fig.9 The σ-ε curves at ε=1300s^-1

《表1》

表1 动态拉伸屈服限Y与应变率ε及温度T的关系

Table1 Relation of dynamic yielding limit Y with strain rate ε and temperature T

《3 材料动态拉伸本构行为描述》

3 材料动态拉伸本构行为描述

采用两种本构模型来表述材料在塑性失穗发生前的本构行为,其一是基于工程及数值模拟计算需求,参照Bodner-parton理论提出的唯象模型,其二考虑热力耦合效应建立的含温度的三项式本构方程。

《3.1 唯象的Bodner-Parton模型》

3.1 唯象的Bodner-Parton模型

鸽合金是由体积分数约占85.4%的钨颗粒及14.6%的W-Ni-Fe粘结相高温烧结而成,具有相当复杂的细观结构,再加上高频冷锻作用,合金的微观组织又发生了进一步的变化,所以若要从细观变形的规律性出发来确立其本构模型是相当困难的。焦彤、熊映明等^[6,7]曾作过一些尝试。

根据工程使用需求,以冲击拉伸试验数据为依据,参照Bodner-Parton模型建立一种唯象的、能再现材料冲击拉伸行为的本构关系。因为试验数据表明,锻造态钨合金具有明显的应变率相关特性,但其初始变形仍为弧形上升的,动态屈服点并不十分明确,而B-P模型恰恰适用于这类材料力学性态的表述。

我们知道,材料的应变率ε_ij各可分为弹性应变率\(\dot{\varepsilon}_{i j}^{\mathrm{e}}\)和非弹性应变率\(\dot{\varepsilon}_{i j}^{p}\)两部分,即

\(\dot{\varepsilon}_{i j}=\dot{\varepsilon}_{i j}^{\mathrm{e}}+\dot{\varepsilon}_{i j}^{\mathrm{p}}\) (4)

其中弹性应变率服从广义虎克定律

\(\dot{\varepsilon}_{i j}^{\mathrm{e}}=\frac{\dot{\sigma}_{i j}}{2 \mu}-\frac{\lambda \dot{\sigma}_{k k} \delta_{i j}}{[2 \mu(3 \lambda+2 \mu)]}\)。（5）

式中λ,μ为Lame常数,μ可用材料的剪切模量代替。

非弹性应变率张量的二次不变量I₂与应力偏张量的二次不变量J₂有下列关系

\(\begin{aligned} I_{2}^{2} &=I_{0}^{2} \exp \left[-\left(A^{2} / J^{2}\right)^{n}\right] \\ A^{2} &=\frac{1}{3} Z^{2}\left(\frac{n+1}{n}\right)^{\frac{1}{n}} \\ Z &=Z_{1}+\left(Z_{0}-Z_{1}\right) \exp \left(-m W_{\mathrm{p}} / Z_{0}\right) \end{aligned}\) 。（6）

n与I₂ - I₂曲线的届服极限变化程度及应变率的敏感性有关;I₀为应力很高时的极限值;Z为与材料的屈服限有关的内变量,它是塑性比功W_P,的略数;Z₀、Z₁和m都是材料参数。

在单向应力情况下,式(6)简化为

\(\dot{I}_{2}^{2}=I_{0}^{2} \exp \left[-\left(3 A^{2} / \sigma^{2}\right)^{n}\right.\) （7）

此时,非弹性应变率偏量为

\(\dot{\varepsilon}_{x}^{p}=\frac{2 I_{0}}{\sqrt{3}} \cdot \frac{\sigma}{|\sigma|} \exp \left[-\frac{1}{2}\left(\frac{3 A^{2}}{\sigma^{2}}\right)^{n}\right]\\ \dot{\varepsilon}_{y}^{p}=\dot{\varepsilon}_{z}^{p}=-\frac{1}{2} \dot{\varepsilon}_{x}^{p}\)。（8）

在拉伸条件下,σ/|σ|=1。

图10至图13为利用参数优化方法拟合得到的各种应变率下不同温度的。σ-ε 曲线。拟合得到的参数分别为Z₀=0.439 N/mm²,Z₁=2.3041 N/mm²,I₀=10265s^-2,n=18001;m=21025。各图的曲线表明,本构计算曲线与实验曲线符合地很好。

《图10》

图10 σ-ε曲线(ε=100s^-1)

Fig.10 σ-ε curve at ε=100s^-1

《图11》

图11 σ-ε曲线(ε=300s^-1)

Fig.11 σ-ε curve at ε=300s^-1

《3.2 冲击拉伸的热力耦合本构》

3.2 冲击拉伸的热力耦合本构

由于冲击拉伸实验时变形极为快速,故可视为绝热过程,在此过程中,既有材料的应变硬化及应变率硬化效应,同时还存在着冲击热软化效应。在建立描述材料动态响应行为的本构时必须考虑它们的耦合作用。Shirkashi等吊曾提出一种把三种效应解耦的粘塑性本构的经验公式,其形式为\(\sigma=X(\varepsilon) Y(\dot{\varepsilon}) Z(T)= \\ A \varepsilon^{n} \dot{\varepsilon} \exp \left[-\lambda\left(T-T_{0}\right)\right]\)。（9）

《图12》

图12 σ-ε曲线(ε=900s^-1)

Fig.12 σ-ε curve at ε=900s^-1

《图13》

图13 σ-ε曲线(ε=1300s^-1)

Fig.13 σ-ε curve at ε=1300s^-1

其中c为单轴拉伸流动应力,A,n,力,2为材料常数,工和Tu分别为材料在拉伸时的瞬态温度及初始温度。按照式(9)的基本思想,提出了如下多项式形式的本构方程

\(\sigma=\left(\sigma_{0}+E_{1} \varepsilon+E_{2} \varepsilon^{2}+E_{3} \varepsilon^{3}\right)\left(\frac{\varepsilon}{\dot\varepsilon_{0}}\right)^{m} Z(T)\)。 (10)

其中\(\sigma_{0}\)和\(\dot\varepsilon_{0}\)为参考屈服应力和应变率,E₁,E₂,E₃为硬化系数。由于受拉伸试件的瞬态温度很难精确测量,为此,提出从塑性功计算温度T的修正方法,即

\(\mathrm{d} T=\frac{1}{\rho c} \sigma \mathrm{d} \varepsilon \) (11)

其中\(\rho, c\)分别表示试样的密度及比热。将式(11)代人式(10)得到

\(\sigma=X(\varepsilon) Y(\dot{\varepsilon}) \exp \left(-\frac{\lambda}{\rho c} \int_{0}^{\epsilon} \sigma \mathrm{d} \varepsilon\right)\) (12)

或\(\sigma=X(\varepsilon) Y(\dot{\varepsilon}) \exp \left(\beta T_{0}^{a} W_{\mathrm{P}}\right)\), (13)

其中\(\beta , a\)为经验常数,W_p为塑性功。这样,就可以从塑性功得到热软化项中的温度T而不需要直接测量它。由此,便可以从一组\(\sigma(t),\varepsilon(t) ,\dot{\varepsilon}(t)\)测量数据,借助于优化拟合方法获得给定材料的本构方程参数。对于鸨合金,其本构参数为,\(\sigma_{0}\)=0.0264 GPa,E₁=168.97GPa,E₂=-3551.40GPa,E₃=8.24GPa,m=0.0943,\(\beta\)=29.96m/J·K,a=0.0381。

《3.3 塑性失稳发生的条件及临界失稳应ε1的确定》

3.3 塑性失稳发生的条件及临界失稳应ε₁的确定

所建立的本构方程不能预告临界失稳应变ε₁的数值。白以龙^[9]以及Nojimao^[10]曾提出一种考虑热效应影响的拉伸失稳判据,其形式为

\(\left(\frac{\partial \sigma}{\partial \varepsilon}\right)_{\dot{\varepsilon}, T}-\left[1-\frac{1}{\rho c}\left(\frac{\partial \sigma}{\partial T}\right)_{\varepsilon, \dot{\varepsilon}}\right] \sigma=0\)。（14）

对于给定的本构方程\( \sigma=X(\varepsilon) Y(\dot{\varepsilon}) Z(T) \),可得到

\(\frac{X^{\prime}(\varepsilon)}{X}+\frac{\sigma}{\rho c} \frac{Z^{\prime}(T)}{Z}=1\)。 (15)

把式(11)代人式(15)中,得到

\(\frac{\mathrm{d} X}{X}+\frac{\sigma}{Z} \frac{\mathrm{d} Z}{\mathrm{~d} W_{\mathrm{P}}} \mathrm{d} \dot{\varepsilon}=\mathrm{d} \varepsilon\)。 (16)

通常情况下,可以用指数形式表示Z(W_p),即

\(Z\left(W_{\mathrm{P}}\right)=\exp \left(-\frac{\lambda}{\rho c} W_{\mathrm{P}}\right) \)。 (17)

用多项式表示\(X(\varepsilon) \)为

\(X(\varepsilon)=A_{0}\left(A_{1}+A_{2} \varepsilon\right)^{k}\), (18)

其中\( A_{0}, A_{1}, A_{2}, k \)皆为材料常数,给定了式(17)和式(18),而后积分式(16),得到

\(\ln \frac{X\left(\varepsilon_{1}\right)}{X_{0}}-B W_{1}=\varepsilon_{1} \), (19)

式中\(a=\frac{k}{B}, \quad b=\frac{k A_{2}-A_{1}}{B A_{1}} ，W_{1}\)为发生塑性失稳时的最大载荷。进而得到

\(\begin{array}{l} k \ln \left(1+\frac{A_{2}}{A_{1}} \varepsilon_{1}\right)= \\ k\left[1+\frac{A_{2}}{A_{1}} \varepsilon_{1}-\left(\frac{A_{2}}{A_{1}} \xi\right)^{2}\right]=B W_{1}+\varepsilon_{1}, \end{array}\) (20)

其中\(0 \leqslant \xi \leqslant \varepsilon_{1} \)。通常情况下\( \varepsilon_{1}<<1 \),并且钨合金的\(\varepsilon_{1}<0.10 \),则式(20)以足够的精度表示为

\(W_{1}=\frac{k}{B}+\frac{k A_{2}-A_{1}}{B A_{1}} \varepsilon_{1}=a+b \varepsilon_{1},\) （21）

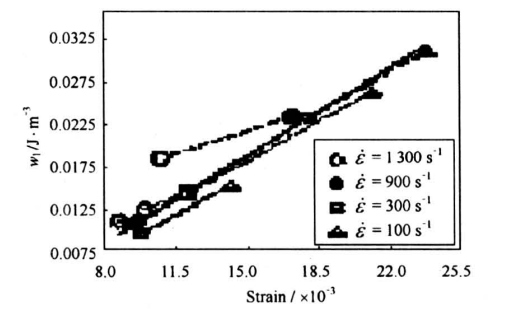
其中 \( a=\frac{k}{B}, b=\frac{k A_{2}-A_{1}}{B A_{1}} \) 。显然, 该式表明\( W_{1} \)与\(\varepsilon_{1}\)存在着线性关系。有趣的是,图14所示的实验结果给式(21)的线性规律以强有力的支持,用最佳拟合方法获得的线性关系为

\(W_{1}=a+b \varepsilon_{1}= \\ -0.00184+1.346 \varepsilon_{1}\left(\mathrm{~J} / \mathrm{m}^{3}\right) \), (22)

该式的相关系数达到0.9947。这样,利用式(13)求得W_p,进而与式(12)的计算值比较,得出发生塑性失稳的判据为

\(W_{\mathrm{P}}<a+b \varepsilon_{1}\), (23)

《图14 》

图14 失稳时塑性功与应变率关系

Fig.14 Relation between plastic work and strain rate at the plastic instability

图15给出了计算与实验结果的比较。它们表明，用上述方法算得的结果与实验获得的σ-ε曲线在ε≤ε1之前符合地非常好。

《图15》

图15 实验与计算结果的比较

Fig.15 Comparison of the calculation with experimental data

《4 动态拉伸断口的分形分析》

4 动态拉伸断口的分形分析

断口表面的分形分析是研究材料变形与断裂细观特性与力学性态间关系的重要方法。大量研究表明，断口表面的粗糙度乃是材料断裂机制的重要反映，并且同材料的力学特性具有相关性。Mandelbrot等^[11]最早用分形理论来描述断口表面的特征,他指出,分形维数可以当作描述材料断口形状的一个重要的特性参数。

大量实验观察断口的形貌表明,裂纹的路径往往是以“Z“字形扩展的,如图16所示,并且具有统计的自相似性。按照分形理论,相似维数D_f可定义如下;

\(D_{\mathrm{f}}=\frac{\ln N}{\ln (1 / \beta)}=-\frac{\ln N}{\ln \beta} \), (24)

其中N为局部客体的个数,\(\beta\)为局部与整体的相似比。

《图16》

图16 断口的形貌图

Fig.16 Morphologies of tensile fracture for 93wt.% W-alloy

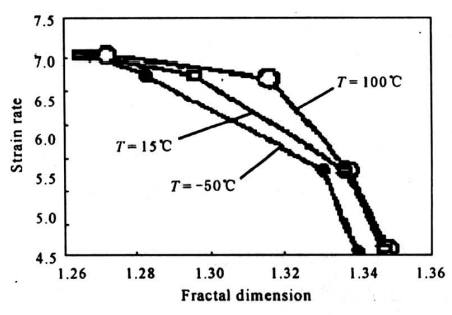
钨合金有两种断裂模式，一种是沿钨颗粒与粘结基体相的晶界断裂的模式1，另一种是所谓穿晶断裂模式2。而每一种断裂模式在整个断口表面上所占的分数是和应变率紧密相关的。断裂模式2的增多就意味着材料韧性变好。反之，则认为材料变脆。选择模式2的分形维数来描述断口的形貌。寻求分形维数的方法是这样做的：a.从每个试样断口上选10个视场并放大500倍；b．把整个断口划分成边长为3μm的小方格，如图17所示。然后统计模式2的小方格数所占的分数，这就是式（24）中的1／β。同时统计出整个断口照片的小方格数目N；c.另外，对不同温度和应变率条件下检测的试样的断口作类似的统计，所获得的结果展示于图18。从中可以看到，在某一特定温度下，分形维数D1是随着应变率e的提高而减小的；温度由-50℃变到100℃时，分形维数D1是变大的。鉴于D1是断口表面粗糙度的量度，分形维数D1愈大，则断口表面的粗糙度愈大，表明材料的韧性愈好。因此，上述结果表明，钨合金材料的韧性是随着应变率的提高而变坏的，而在同一应变率下则随着温度的提高，韧性是变好的，这一分析结论与力学实验的宏观结果取得相当好的一致。

《图17 》

图17 分形维数的测量准则

Fig.17 The method of measuring fractal dimensions

《图18》

图18 分形维数和应变率的关系

Fig.18 Relation of fractal dimension with strain

《5 简要分析与结论》

5 简要分析与结论

1）对钨质量分数为93％的锻造态钨合金的动态拉伸性能进行了较为系统的测试，给出了不同温度和不同应变率下的σ-ε曲线。实验表明，钨质量分数为93％的钨合金表现出明显的率敏感性和温度效应。材料的动态断裂应变E1随着温度的升高而增大，这可从屈服后的塑性平台随温度提高逐渐拉长上看的更清楚。由数据给出，在e＝100s-＇时，从-50℃时的ε1＝1.4％到100℃时的3.4％，增加量达71.4％，表明，材料的韧性受温度影响很大。但是，动态屈服限的数据表明，在同一应变率下，温度变化的影响却不明显，如e＝100s时，-50℃，15℃，100℃时的屈服限分别为1.34 GPa，1.31 GPa和1.30 GPa；再如e＝ 1300s-＇时的屈服限分别为1.77 GPa，1.79 GPa，1.78 GPa。这表明，应变率引起的材料的硬化效应和提高温度引起的热软化效应相比，在较低应变率时后者稍占优势，而在较高应变率时前者稍占优势。

2）从实验得到的一系列σ-ε曲线中可以看到一种现象，即材料屈服后的塑性平台随着温度提高不但有展宽现象，而且有向下倾斜的现象。这是由下面的两个原因造成的，其一是在从变形向断裂演化的后期，冲击热软化效应进一步耦合进来，使热软化效应得到更明显的展现；其二是塑性变形后期试件开始发生颈缩，引起了流动应力的降低。

3）依据实验数据提出并建立了两种本构关系。其中基于B-P模型建立的本构关系能较好的描述无明显动态屈服限材料（钨质量分数为93％的钨合金是其中之一）的动态力学响应特性，并具有简单实用的特点。而考虑热与力耦合提出的第二模型，则能较好地描述材料应变硬化、应变率硬化及温度和冲击热软化三者耦合效应对材料动力学性态的影响，特别是它可以在不测量受试材料瞬态温度条件下来计算温度对流动应力的影响，是一种既有学术价值又具有实际应用意义的结果。

4）建立了该合金材料发生塑性失稳的最大应变判据，该判据得到了实验结果的强有力支持。

展示更多