《1 引言》
1 引言
在通常的可靠性研究中,一般假设样本个体的寿命独立同分布。事实上,该假设在某些情况下是值得怀疑的。特别是在许多需要建立回归模型以考察样本寿命与某些伴随变量(也称回归变量)之间关系的场合,设个体寿命的分布依赖于给定的(通常是已知且可测的)伴随变量且将回归变量引入寿命描述的方法虽然较单变量的模型更为有效,但对那些未知或不可测的随机效应却显得无能为力。比如,当考察不同环境(如不同的温度、湿度、振动、辐射等)条件下同种元器件的寿命差异时,环境变量的相互作用会产生某些未知或不可测的随机效应(高温和湿度同时作用会提高湿气的浸透速度和腐蚀影响,低温和低压同时作用会加速密封漏气等),此时,尽管相同环境条件下的个体寿命仍然独立,这些随机效应也可能并非研究中所考察的对象,其存在与否也并不为研究人员所关心,但这种未知或不可测的影响往往导致了基于不同环境条件的样本子组之间存在某种相关性。如果忽略这些随机效应产生的影响,会对个体寿命的估计产生误导[1~3] 。
越来越广泛的用于描述子组中个体寿命之间相关性的模型被称为异质性模型(frailty model);异质性(frailty)即指子组内每个个体都受影响的未知或不可测的随机效应,考虑了异质性的可靠性模型目的是减少随机效应所引起的方差[2] 。近年来,国外涌现了大量针对各种异质性模型研究的文献[4~9];在我国,基于异质性的研究还刚刚起步,其应用也仅仅局限于生物统计方面。
为了适应小子样的情况以及充分利用已有的验前信息,将贝叶斯方法应用于异质性模型中,在样本寿命服从 Weibull 分布的条件下,构建出基于 Gamma 异质性因子的 Weibull 共享异质性模型[3~5],给出随机截尾条件下有关可靠性参数的估计,并借助基于 Gibbs 抽样的马尔可夫链蒙特卡罗(MCMC,Markov chain Monte Carlo)方法[3,10] 以及 BUGS/WinBUGS(Bayesian inference using Gibbs sampling)软件[8,10,11] 解决了传统贝叶斯分析中高维数值积分的困难,提高了计算的精度。
《2 马尔可夫链蒙特卡罗(MCMC)模拟》
2 马尔可夫链蒙特卡罗(MCMC)模拟
MCMC 模拟是一种特殊的蒙特卡罗方法,它将随机过程中的马尔可夫过程引入蒙特卡罗模拟中,从而实现抽样分布的动态模拟。本质上,MCMC 方法是使用马尔可夫链的蒙特卡罗积分。基于贝叶斯推断原理的 MCMC 方法主要用于产生后验分布的样本,计算边缘分布以及后验分布的矩。设 k 维随机向量 U = U1,…,Uk 具有联合分布 π(U1,…,Uk),其中,Uk 为模型参数或缺失的观测值,π(·)为后验分布。对于感兴趣的函数 h(U)的数学期望为

而实际中,该积分往往形式复杂难于计算,此时应采用蒙特卡罗积分进行近似,即:
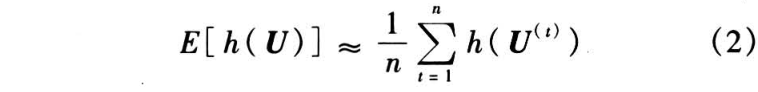
当 U1,…,Uk 相互独立时,由大数定律知,样本容量 n 越大,其近似程度越高。但在很多复杂模型中,不能简单对 U1,…,Uk 做出相互独立的假设,需要使用马尔可夫链蒙特卡罗稳态模拟方法。
MCMC 方法的基本思想是:建立一个马尔可夫链对未知变量 Uk 进行模拟,当链达到稳态分布时即得所求的后验分布。随机点 Uk 来自于分布 π(U),不同的抽样方法导致了不同的 MCMC 方法,如 Gibbs 抽样方法、etropolis-Hastings 方法、以及各种复合方法等。
Gibbs 抽样是最简单也是应用最广泛的一种抽样方法。在上述假设条件下,令 Uj 代表一种随机变量或同组的几个随机变量;第 j 组变量的边缘分布为 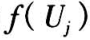 。在给定其余变量的情形下,
。在给定其余变量的情形下,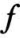 (Uj /U1,…,Uj -1,Uj +1 ,…,Uk)代表了全条件分布密度。给定任意初始向量 U (0) = (U1(0),…,Uk(0)),Gibbs 抽样的第一次迭代如下:
(Uj /U1,…,Uj -1,Uj +1 ,…,Uk)代表了全条件分布密度。给定任意初始向量 U (0) = (U1(0),…,Uk(0)),Gibbs 抽样的第一次迭代如下:

其中“~”表示其左边从其右边抽取得到。由上完成了由 U (0) 到 U (1) =(U1(1),…,Uk (1) )的转移。经过 t 次迭代,可以得到 U (t ) =(U1(t ),…,Uk (t )),并最终得到 U (1),U (2),U (3),… 。由不同的 U (0)出发,马尔可夫链经过一段时间的迭代后,可以认为各时刻U (t )的边际分布为平稳分布,此时它收敛。而在收敛出现前的 m 次迭代中,各状态的边际分布还不能认为是 π(U),因此在估计E [ h(U)]时应将前 m 个迭代值去掉,即

《3 Weibull 共享异质性模型的贝叶斯分析》
3 Weibull 共享异质性模型的贝叶斯分析
《3.1 共享异质性模型》
3.1 共享异质性模型
共享异质性模型(shared frailty model)是异质性模型族中最基本的一种,它是比例危险率回归模型的扩展[3~5]。该模型中假设所存在的随机效应由两部分组成:其一是描述子 1 组之间差异的异质性因子;其二是以样本危险率函数表示的个体随机方差。设第 i 个子组中第 j 个个体的危险率函数为

其中 i = 1,...,n,j = 1,...,m;h0(t)为比例危险率回归模型中的基准危险率;xij 为 p × 1 维伴随变量,代表了影响不同个体寿命分布的主要因素;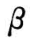 为 p × 1 维回归系数向量,它刻画了伴随变量影响程度的大小;
为 p × 1 维回归系数向量,它刻画了伴随变量影响程度的大小; 为第 i 个子组的异质值,来自独立同分布的样本
为第 i 个子组的异质值,来自独立同分布的样本 。为了便于分析,也可将式(4)写作
。为了便于分析,也可将式(4)写作

其中,异质值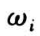 来自独立同分布的样本
来自独立同分布的样本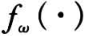 。
。 与
与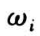 反映了不同子组之间的相关性,且被同一子组内的个体所“共享”。通常,称具有式(4)所描述的危险率模型为加法异质性模型,而称具有式(5)所描述的危险率模型为乘法异质性模型。
反映了不同子组之间的相关性,且被同一子组内的个体所“共享”。通常,称具有式(4)所描述的危险率模型为加法异质性模型,而称具有式(5)所描述的危险率模型为乘法异质性模型。
《3.2 Gamma 异质性模型》
3.2 Gamma 异质性模型
描述异质性因子的模型包括单参数 Gamma 分布、正则稳态分布、对数正态分布、逆高斯分布、均匀分布等[4~9],其中以单参数 Gamma 分布构成的 Gamma 异质性模型最常用。在 Gamma 异质性模型中,设异质性因子 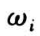 独立同分布于单参数 Gamma 分布,记为
独立同分布于单参数 Gamma 分布,记为  ,其概率密度函数为
,其概率密度函数为
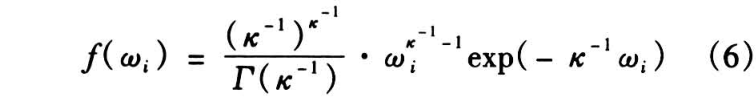
其中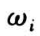 的均值为 1,方差为
的均值为 1,方差为 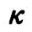 。不难看出,
。不难看出,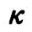 的值越大,反映子组间的异质性越强,同时,子组内的相关性也越强。令
的值越大,反映子组间的异质性越强,同时,子组内的相关性也越强。令  ,得出
,得出
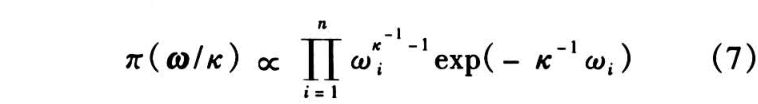
《3.3 随机截尾的 Weibull 共享异质性乘法模型及其贝叶斯分析》
3.3 随机截尾的 Weibull 共享异质性乘法模型及其贝叶斯分析
可靠性分析中的寿命数据通常具有截尾的特性,即只知道样本个体中一部分确切的寿命值,而剩余部分的寿命只知其超过某一特定值。截尾方式的不同导致不同的寿命试验及研究方法的各异[12] 。随机截尾试验是很简单且经常可实现的一种研究过程:在共享异质性模型中,假设每个样本个体具有寿命 T 和截尾时间 L,且 T 和 L 是独立的连续随机变量。设试验中仅能观测到第 i 组中第 j 个样本个体的产品寿命  ,该式表明若
,该式表明若  >
>  则第 i 组第 j 个样本在
则第 i 组第 j 个样本在 后失去观察。规定
后失去观察。规定  为指示变量,当
为指示变量,当 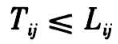 ,
,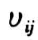 = 1,当
= 1,当  >
>  ,
,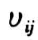 = 0。于是,似然函数为
= 0。于是,似然函数为

假设个体寿命 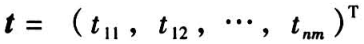 服从二参数 Weibull 分布,记为
服从二参数 Weibull 分布,记为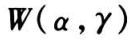 ,则其概率密度为
,则其概率密度为
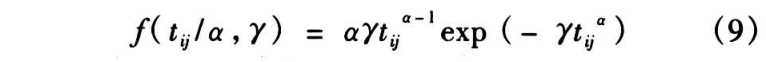
分布函数与生存函数为
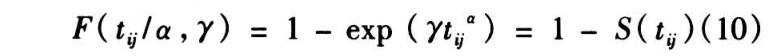
基准危险率函数为
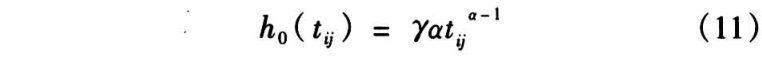
将式(11)代人式(5),不难得出在给定第 i 个子组的异质性因子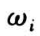 以及伴随向量
以及伴随向量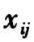 条件下样本个体寿命
条件下样本个体寿命 的条件危险率函数如下:
的条件危险率函数如下:
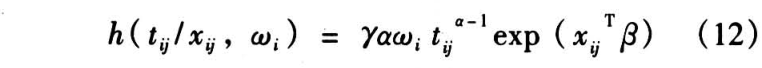
为便于分析,记  ,式(12)也可化为
,式(12)也可化为 ,则个体寿命
,则个体寿命 服从二参数 Weibull 分布
服从二参数 Weibull 分布  ,该式即为 Weibull 共享异质性乘法模型。记
,该式即为 Weibull 共享异质性乘法模型。记 
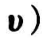 该模型的完备数据集,得其似然函数为
该模型的完备数据集,得其似然函数为
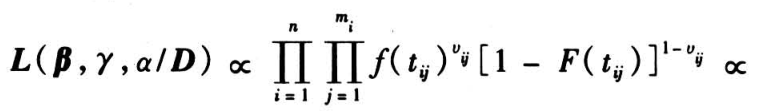
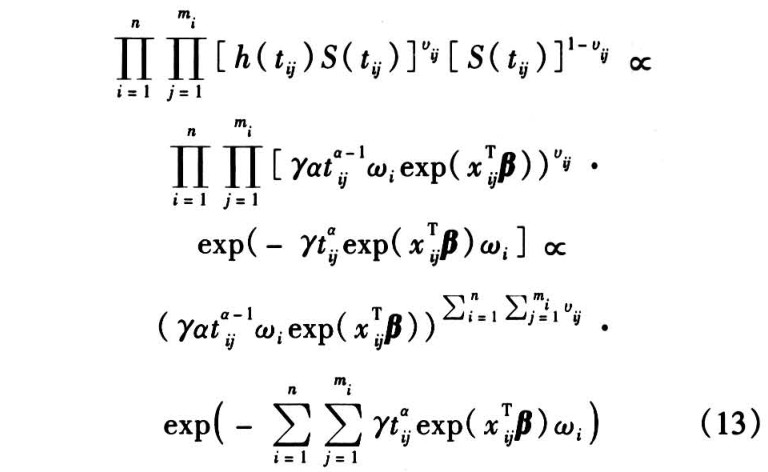
记 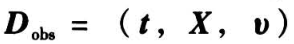 为模型的观测数据集,则
为模型的观测数据集,则 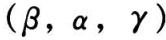 基于 Dobs 的似然函数可以通过对式(13)与式(7)的积分获得。显然,明确写出该积分形式的解析表达式是很困难的,因此,基于传统的高维数值积分方法很难得出
基于 Dobs 的似然函数可以通过对式(13)与式(7)的积分获得。显然,明确写出该积分形式的解析表达式是很困难的,因此,基于传统的高维数值积分方法很难得出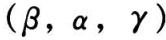 的联合后验分布。这里,利用 Gibbs 抽样方法得出参数联合后验分布的抽样。令 π(·)代表有关参数的先验分布,则异质性因子
的联合后验分布。这里,利用 Gibbs 抽样方法得出参数联合后验分布的抽样。令 π(·)代表有关参数的先验分布,则异质性因子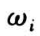 的条件分布形式如下:
的条件分布形式如下:
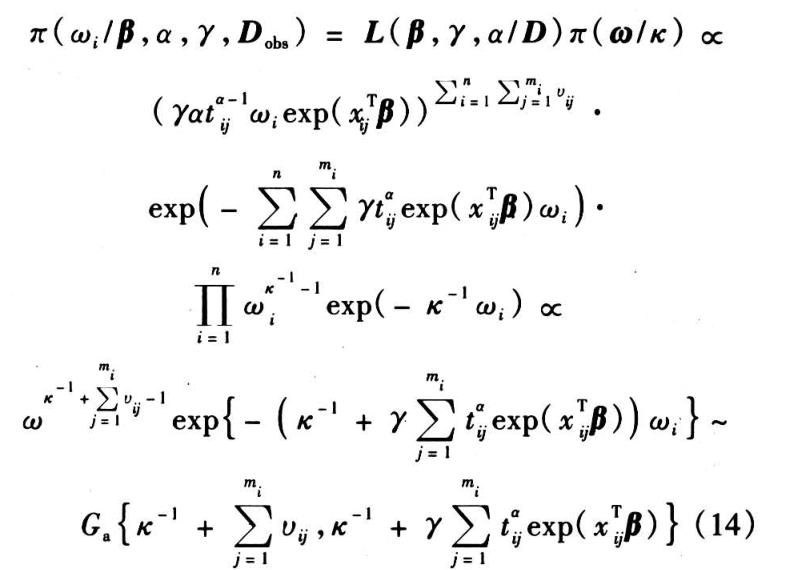
设  的先验分布为
的先验分布为  则
则
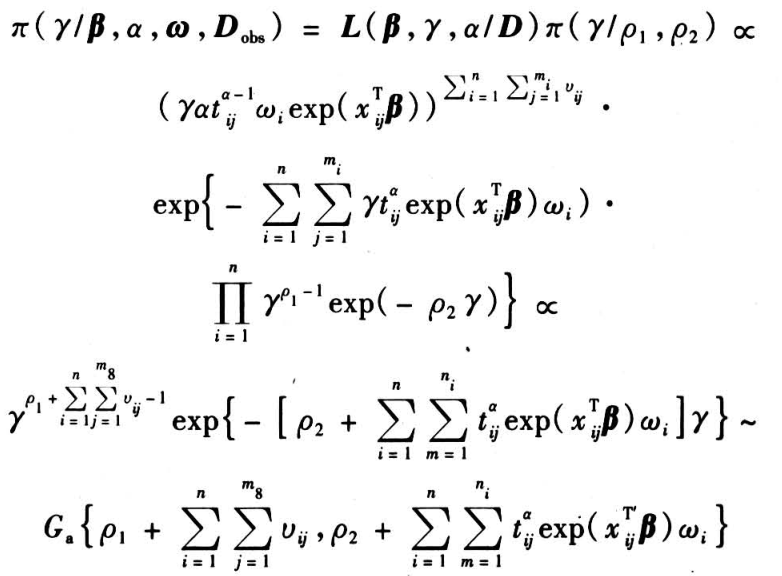
设  ,同上可得
,同上可得

《4 数据仿真分析》
4 数据仿真分析
《4.1 仿真数据》
4.1 仿真数据
假定某种产品的寿命  服从 Weibull 分布
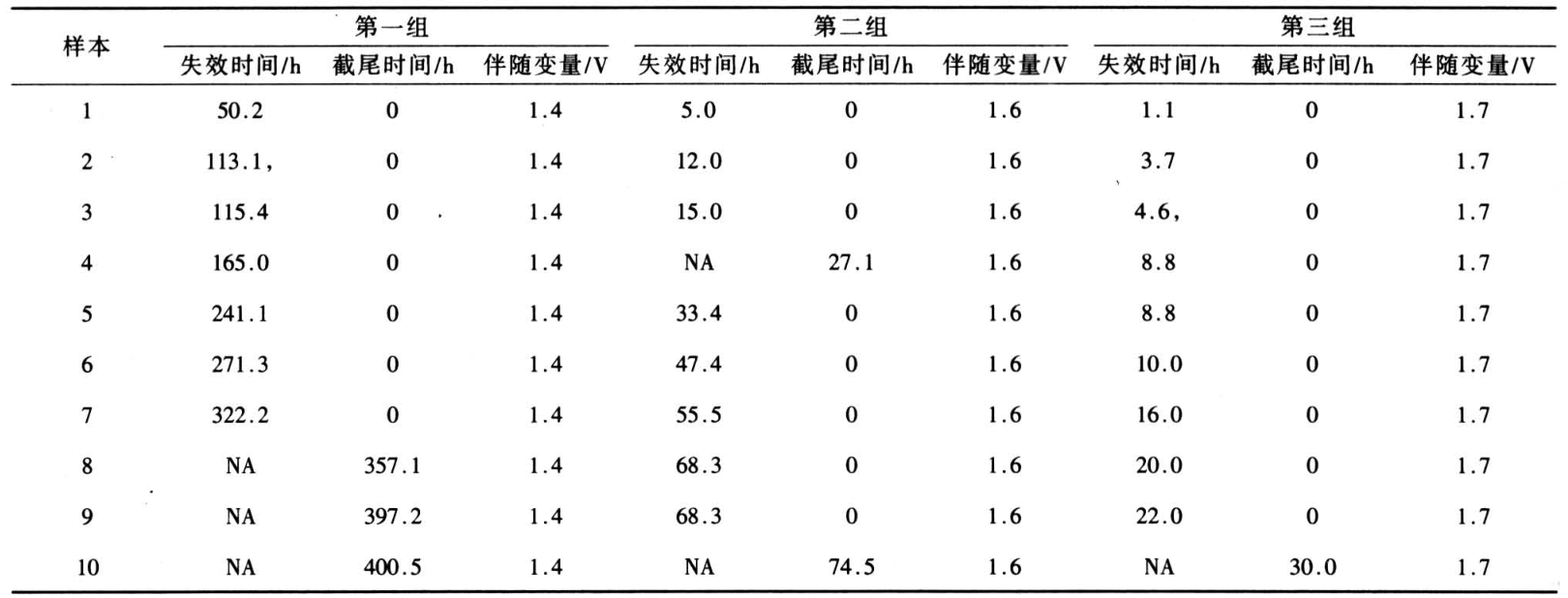
服从 Weibull 分布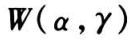 ,为了考察该产品在不同的电压水平中寿命的差异,取样本容量30,分成三组分别暴露于电压水平 V = 1.4,1.6,1.7 V 中,则
,为了考察该产品在不同的电压水平中寿命的差异,取样本容量30,分成三组分别暴露于电压水平 V = 1.4,1.6,1.7 V 中,则 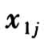 = 1.4,
= 1.4,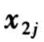 = 1.6,
= 1.6,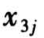 =1.7(表 1)。在观察周期内记录个体失效的时间
=1.7(表 1)。在观察周期内记录个体失效的时间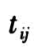 记为
记为 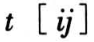 ;在观测结束时发生失效的时间视为有效数据,尚未失效的产品寿命是被随机截尾的,记为 NA;只知其寿命值不低于对其观测的时间
;在观测结束时发生失效的时间视为有效数据,尚未失效的产品寿命是被随机截尾的,记为 NA;只知其寿命值不低于对其观测的时间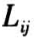 ,记为
,记为 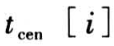 ;伴随变量电压水平
;伴随变量电压水平 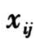 的
的
系数用 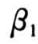 来表示。设第 i 组的异质性因子
来表示。设第 i 组的异质性因子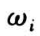 服从单参数 Gamma 分布,由此可得基于式(12)的一元 Weibull 共享异质性模型模型。
服从单参数 Gamma 分布,由此可得基于式(12)的一元 Weibull 共享异质性模型模型。
《表 1》
表 1 随机截尾试验中产品寿命的仿真数据
Table 1 Simulated data for product's lifetime with random truncated test
《4.2 参数后验分布的 Gibbs 抽样》
4.2 参数后验分布的 Gibbs 抽样
在本例中,根据上述有关参数的贝叶斯后验分析可得基于 Gibbs 抽样的 MCMC 模拟过程是:给定  的任意初始值,记为
的任意初始值,记为 
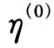 ,则 Gibbs 抽样的第一次迭代如下:
,则 Gibbs 抽样的第一次迭代如下:

由上完成了由  到
到 
 最终可根据式(3)得到参数的后验估计。
最终可根据式(3)得到参数的后验估计。
《4.3 基于 WinBUGS 的建模分析》
4.3 基于 WinBUGS 的建模分析
BUGS/WinBUGS 是英国剑桥公共卫生研究所推出的利用 MCMC 方法进行贝叶斯推断的专用软件包,使用 WinBUGS 可以很方便地对许多常用的模型和分布进行 Gibbs 抽样,编程者只要设置好变量的先验分布并对所研究的模型进行一般性描述,就能很容易实现对模型的贝叶斯分析[8],WinBUGS 中可以使用有向图模型方式(DAG,directed acyelic graphical model)对模型进行直观的描述(图 1),也可以直接编写模型程序。Gibbs 抽样收敛后,可以得到参数的后验分布的均值、标准差、95% 置信区间和中位数等信息(表 2),并给出后验分布的核密度估计图(图 2)、参数的 Gibbs 抽样动态图(图3)等,使抽样结果更直观、可靠。基于表 1 所示的仿真数据,构建如上 Weibull 共享异质性模型模型,截取前1 000次迭代结果,从第1 001次开始进行5 000次迭代分析。
《图 1》
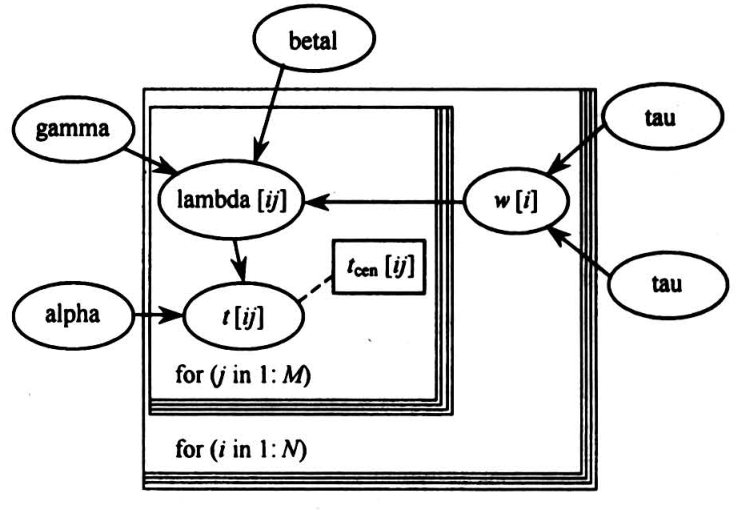
图 1 WinBUGS 中的贝叶斯有向无环图
Fig.1 Bayesian directed acyclic graphical model in WinBUGS
从表 2 的 WinBUGS 运行结果,不难得到 α 的均值为 1.279,95% 置信区间为(0.8746,1.703), 的均值为 7.521,95% 置信区间为(-1.555,14.97)等;特别地,可以清楚地看出,当
的均值为 7.521,95% 置信区间为(-1.555,14.97)等;特别地,可以清楚地看出,当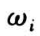 的取值大于 1 时,该组中个体失效的速度会倾向于比独立模型中以
的取值大于 1 时,该组中个体失效的速度会倾向于比独立模型中以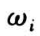 概率取 1 时的速度更快,反之,当
概率取 1 时的速度更快,反之,当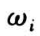 的取值小于 1 时,该组中个体预期的寿命将大于采用独立模型所预期的寿命。此外,WinBUGS 的运行结果还可显示 Gibbs 抽样后的抽样值自相关图及均值和置信区间的变化图等(仅列出其中一部分)。
的取值小于 1 时,该组中个体预期的寿命将大于采用独立模型所预期的寿命。此外,WinBUGS 的运行结果还可显示 Gibbs 抽样后的抽样值自相关图及均值和置信区间的变化图等(仅列出其中一部分)。
《表 2》
表 2 5 000 次抽样迭代的参数后验估计统计量
Table 2 Posterior estimate statistics for monitored parameters with 5000 iterations

《图 2》


图 2 5 000 次抽样迭代后参数的后验核密度估计
Fig.2 Posterior kernel density estimation for monitored parameters with 5 000 iterations
《图 3》

图 3 参数抽样轨迹图
Fig.3 Trace plots for monitored parameters’iteration
《5 结语》
5 结语
Weibull 共享异质性模型中考虑了样本子组中未知或不可测的随机效应,贝叶斯方法的应用,提高了该模型的有效性。利用基于 Gibbs 抽样的 MCMC 模拟方法与 WinBUGS 软件的应用解决了该模型中高维数值计算的不便,提高了计算的精度,有利于该模型在可靠性分析理论中的推广。仿真实例中的一元 Weibull 共享异质性模型可以推广到多元的情况中去,不难看出,该模型在可靠性分析领域中具有较独立 Weibull 模型更为广“泛的应用前景。
尽管多数文献中普遍假设子组中异质性因子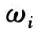 的先验服从单参数的 Gamma 分布,该假设使得模型的分析计算趋于方便,但在许多场合中,其他描述异质性因子的模型(如正则稳态分布,对数正态分布,逆高斯分布等)较Gamma 异质性模型更为有效,更能减少由那些未知或不可测的随机效应所产生的误差,这也是下一步的研究方向。
的先验服从单参数的 Gamma 分布,该假设使得模型的分析计算趋于方便,但在许多场合中,其他描述异质性因子的模型(如正则稳态分布,对数正态分布,逆高斯分布等)较Gamma 异质性模型更为有效,更能减少由那些未知或不可测的随机效应所产生的误差,这也是下一步的研究方向。














 京公网安备 11010502051620号
京公网安备 11010502051620号




