《1 引言 》
1 引言
由结构振动引起的声辐射问题是声学中的一个长期的研究课题。由于结构振动与声辐射之间的耦合作用,使得噪声问题显得更为复杂,因此研究声辐射的机理对噪声的控制及其低噪声设计有着重要的意义。目前,对于大多数工程实际问题,都是利用数值方法(有限元方法、边界元方法、无限元方法、统计能量方法等)或者实验测试来求解结构振动声辐射的,这不利于深入研究弹性结构声辐射产生机理及声-振特性。
实际上,对于一些基本形状体如矩形板、柱面等的声辐射特性的研究已经比较成熟[1 ~ 6] 。但对于考虑规则结构之间连接的振动耦合后的辐射声场的研究还较少。在工程中,机电设备的外部结构基本上是由多个类似的规则结构通过焊接、螺钉连接或其他方式连接在一起。因此,对于规则连接结构的声辐射建模与分析在工程上具有重要的应用价值。
笔者建立了两个封闭弹性长方体连接结构的辐射声场模型,该模型分别考虑了两个弹性长方体结构与声腔的耦合,以及两个弹性体之间的振动的传递;重点讨论了结构之间的连接属性对辐射声场的影响,因此,在模型中只考虑两结构连接面为弹性面,其余均为刚性面,并通过算例分析了辐射声场的特性,讨论了结构之间不同连接条件对辐射声场的影响。
《2 理论推导》
2 理论推导
《2.1 分析模型》
2.1 分析模型
如图 1 所示,两长方体空腔 1 和 2 分别由 1 块四边弹性支承的弹性板及 5 块刚性板密封而成。腔体 1 的长、宽、高分别为  和
和  ,体积为 V1 ,弹性板 1 的厚度为 h1 ,面积为 S1 ,边界为
,体积为 V1 ,弹性板 1 的厚度为 h1 ,面积为 S1 ,边界为 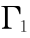 ;腔体 2 的长、宽、高分别为
;腔体 2 的长、宽、高分别为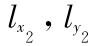 和
和  ,体积为 V2 ,弹性板2 的厚度为 h2 ,面积为 S2 ,边界为
,体积为 V2 ,弹性板2 的厚度为 h2 ,面积为 S2 ,边界为 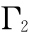 ;板 2 中心点的坐标为(
;板 2 中心点的坐标为(  ,0)。两弹性板的四边以及连接点分别由线弹簧和旋转弹簧相连,其中板 1 的四周由刚度为 K1,C1 的弹簧相连,板 2 的四周由刚度为 K2,C2 的弹簧相连,两板的各个连接点处由刚度为 K ,C 的弹簧相连。假设各弹簧刚度取常数,通过刚度取值的不同,模拟不同的边界条件和连接条件。
,0)。两弹性板的四边以及连接点分别由线弹簧和旋转弹簧相连,其中板 1 的四周由刚度为 K1,C1 的弹簧相连,板 2 的四周由刚度为 K2,C2 的弹簧相连,两板的各个连接点处由刚度为 K ,C 的弹簧相连。假设各弹簧刚度取常数,通过刚度取值的不同,模拟不同的边界条件和连接条件。
《2.2 弹性结构的振动响应》
2.2 弹性结构的振动响应
由分析力学知,图 1 所示的整个弹性结构的汉密尔顿函数可写为
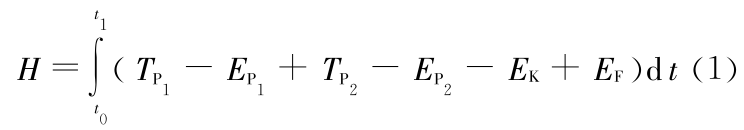
《图 1》
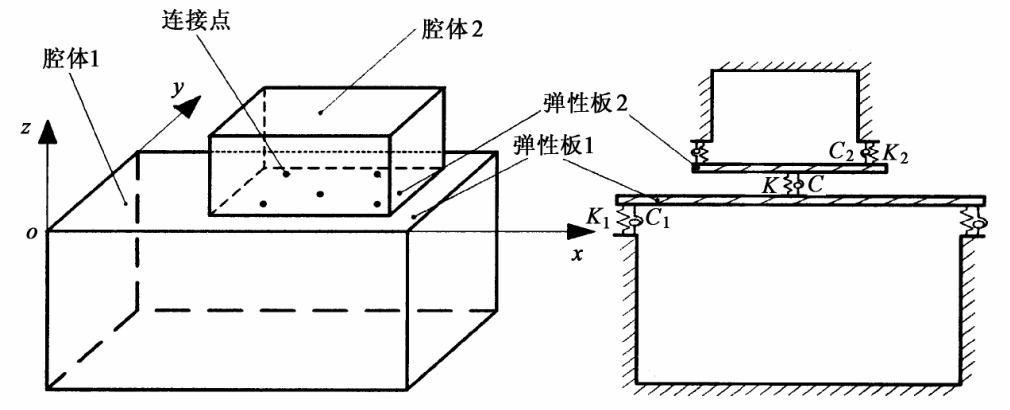
图 1 模型示意图
Fig.1 Schematic diagram of the structure system
由于腔体内的声场与弹性结构之间是强耦合,而腔体外声场与弹性结构之间是弱耦合,故式(1)中不考虑腔体外声场对结构振动的反作用。其中 t1,t2 为任意的时间常数,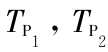 分别为弹性板 1,2 的动能,
分别为弹性板 1,2 的动能, 分别为弹性板 1,2 的势能,其表达式见文献[7] 。EK 为弹簧势能,EF 为外力所做的功:
分别为弹性板 1,2 的势能,其表达式见文献[7] 。EK 为弹簧势能,EF 为外力所做的功:

式中  分别为板 1 和板 2 的弯曲振动的挠度曲线;F1,F2 分别为板 1 和板 2 所受的外力激励;
分别为板 1 和板 2 的弯曲振动的挠度曲线;F1,F2 分别为板 1 和板 2 所受的外力激励; 为矩形腔体 1 ,2 内的声压响应;n 为弹性板 1 和板 2 边界的法线方向;ne 为两结构连接点的 x,y 坐标方向。t 为两结构间的连接点数。由瑞利 - 李兹方法,取两弹性板挠度曲线为
为矩形腔体 1 ,2 内的声压响应;n 为弹性板 1 和板 2 边界的法线方向;ne 为两结构连接点的 x,y 坐标方向。t 为两结构间的连接点数。由瑞利 - 李兹方法,取两弹性板挠度曲线为
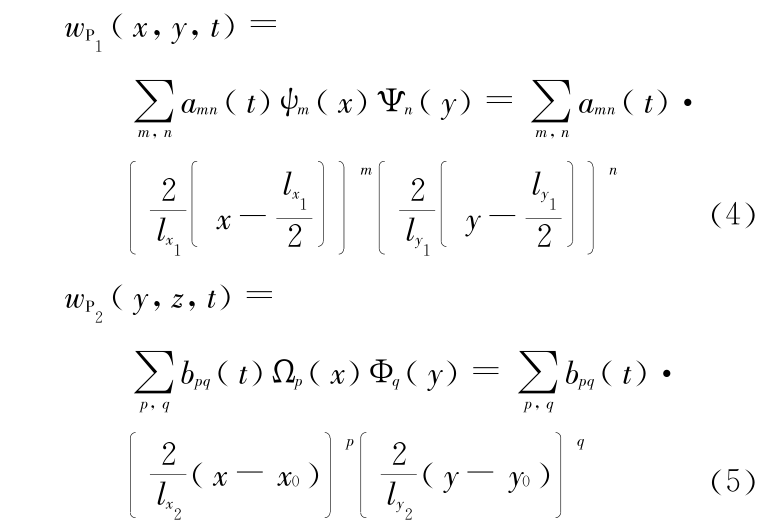
式(4)、式(5)中,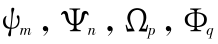 为满足弹性结构位移边界条件的函数,m,n,p,q 为正整数;
为满足弹性结构位移边界条件的函数,m,n,p,q 为正整数;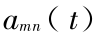 ,
, 为待定系数,考虑简谐激励,令
为待定系数,考虑简谐激励,令 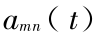 =
=  ,
, =
= 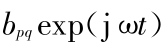 ,ω 为外力激励频率。
,ω 为外力激励频率。
由哈密尔顿原理可知,弹性结构的真实运动应满足

由式(6)推得:
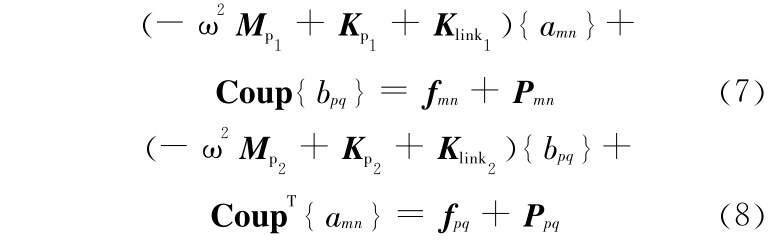


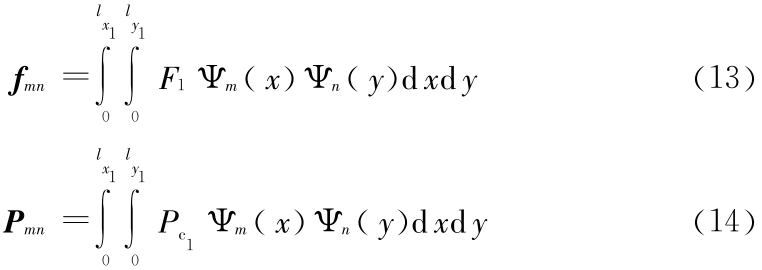
其中 D1 =  ),根据弹性板的弯曲刚度将弹簧刚度表达成无量纲形式,定义 k1 =
),根据弹性板的弯曲刚度将弹簧刚度表达成无量纲形式,定义 k1 =  ,k2 =
,k2 =  ,k =
,k =  ,c1 =
,c1 = 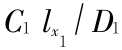 ,c2 =
,c2 =  及 c =
及 c = 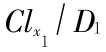 。E1 ,
。E1 ,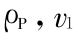 分别为弹性板 1 的杨氏模量、密度和泊松比。
分别为弹性板 1 的杨氏模量、密度和泊松比。
同理,得到  。
。
通过解式(7),式(8)的齐次方程,即可求得两弹性板的固有角频率。
《2.3 矩形腔的声压响应》
2.3 矩形腔的声压响应
根据波动方程,腔体 1 内的声压响应 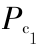 为
为

由边界条件可知,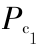 必须满足下列方程:
必须满足下列方程:

将式(16)代入式(17)得

式中 G1 为格林函数。
考虑到矩形腔 1 内的声压响应及格林函数是由刚性边界条件下声腔的各阶固有模态构造而成,即
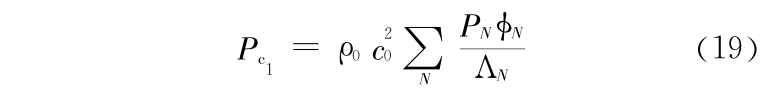
根据理论声学,格林函数为

其中 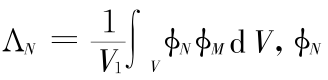
为第 N 阶声模态, 为第 N 阶声模态的固有角频率,PN 为待定的系数。
为第 N 阶声模态的固有角频率,PN 为待定的系数。
将式(19)、式(20)代入式(18)得:


将第 N 阶声模态由相应的正交模态阶数 n1,n2,n3 来代替,声模态及相应的固有角频率见文献[8] 。
将刚性边界条件下的矩形腔的声压模态及固有频率代入式(21),并考虑模态阻尼因子 ,得:
,得:

同理,将矩形腔 2 的第 M 阶声模态由相应的正交模态阶数 m1,m2,m3 代替,推得的声压响应为

将式(22)至式(25)代入式(14)得
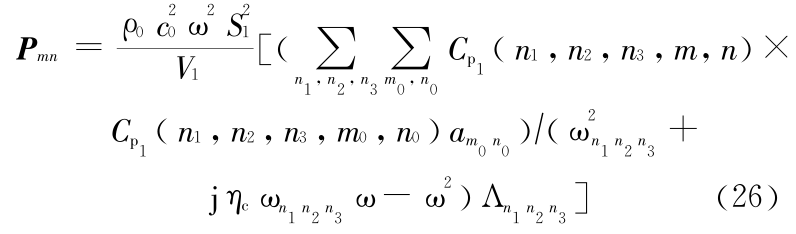
同理得

其中 m0,n0,p0,q0 与 m,n,p,q 意义相同。
将式(26)、式(27)代入式(7)、式(8)联立即可解得弹性板弯曲位移的系数  。
。
《2.4 矩形腔体的外声场》
2.4 矩形腔体的外声场
利用前面已得到的弹性板的表面振动速度求辐射声场。为了书写方便,以下均略去时间因子。对于弹性板 1 ,长方体空腔 1 就好比折叠的障板,由瑞利积分[9] ,得板 1 的辐射声场的声压为
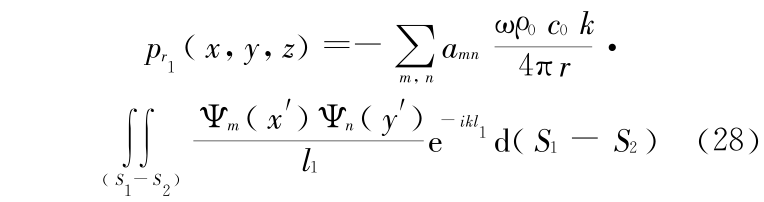
当考虑远场时,从弹性板上各面元发出的声波到达观察点时振幅的差异很小,可近似用观察点到坐标原点的距离 r 代替。相位部分的差异仍需保留。将 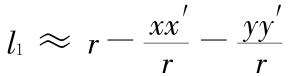 代入式(28),得:
代入式(28),得:



《3 分析算例》
3 分析算例
分析模型为 = 0.7 m × 1.1 m × 0.5 m 及
= 0.7 m × 1.1 m × 0.5 m 及 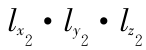 = 0.4 m × 0.3 m × 0.6 m 两长方体封闭声腔,其中两腔体的 z = 0 面为弹性板,其余面均为刚性板;腔体2弹性板的中心坐标为 x0 = 0.3 m , y0 = 0.5 m ;两腔体的连接点坐标为(0.2 m , 0.4 m),(0.38 m , 0.4 m),(0.4 m , 0.45 m),(0.3 m , 0.45 m)。取两弹性板的厚度均为 1 mm ,模型的材料属性如表 1 所示。
= 0.4 m × 0.3 m × 0.6 m 两长方体封闭声腔,其中两腔体的 z = 0 面为弹性板,其余面均为刚性板;腔体2弹性板的中心坐标为 x0 = 0.3 m , y0 = 0.5 m ;两腔体的连接点坐标为(0.2 m , 0.4 m),(0.38 m , 0.4 m),(0.4 m , 0.45 m),(0.3 m , 0.45 m)。取两弹性板的厚度均为 1 mm ,模型的材料属性如表 1 所示。
《表 1》
表 1 材料参数
Table 1 Material parameter

重点考虑的是连接属性对辐射声场的影响,因此,取弹性板为简支边界条件。理论上,板四周的支承线弹簧的刚度无限大,旋转弹簧刚度为 0 时,板为简支的边界条件,实际计算中,取远大于板的弯曲刚度即可。取无量纲形式线弹簧刚度为 0 ~ 5 × 107 ,旋转弹簧刚度为 0 ~ 5 × 105 ,表示不同的连接条件和边界条件。
在板 1 点(0.2 ,0.4 ,0)上作用 10 ~ 600 Hz 范围内的单位简谐力,利用前面推导出的弹性板的辐射声场,由解析表达式计算出腔体外的声压响应的解析解。
取 k1 = k2 = 5 × 107 , c1 = c2 = 0 模拟弹性板简支边界。为了了解连接处线弹簧刚度的取值对辐射声场的影响,在旋转弹簧的刚度值为 c = 5 × 102 的情况下,分别取 k = 0 和 k = 5 × 107 时,声腔外点(5 ,4 ,3.8)声压响应如图 2 所示。
图 2 中连接条件为 k = 0 时的辐射声压总体上明显小于 k = 5 × 107 ,可知连接处线弹簧的刚度变化对结构的辐射声场影响较大。线弹簧的刚度取值愈大,辐射声场的响应愈强。
《图 2》

图 2 k 取不同值时点(5,4,3.8)的声压响应
Fig.2 Sound response of point (5,4,3.8) due to different stiffiness (k)
同样,在连接处线弹簧刚度 k = 5 × 103 取值不变的情况下,分别取 c = 0 和 c = 5 × 105 时,点(5,4,3.8)的声压响应如图 3 所示。
《图 3》

图 3 c 取不同值时点(5,4,3.8)的声压响应
Fig.3 Sound response of point (5,4,3.8) due to different stiffiness (c)
由图 3 可看出,连接条件为 c = 0 时的辐射声压总体上与 c = 5 × 105 时差别很小,可知旋转弹簧刚度的变化对辐射声场的影响不大。与图 2 进行比较可看出,连接弹性板的旋转弹簧的刚度变化对结构的辐射声场的影响较之线弹簧要小得多。
当弹簧刚度分别为 k = 5 × 103 , c = 5 × 102 时,在两板上的重合点(0.2,0.4,0)上分别单独作用 10 ~ 600 Hz 范围内的单位简谐力,声腔外点(5,4,3.8)声压响应如图 4 所示。
《图 4》
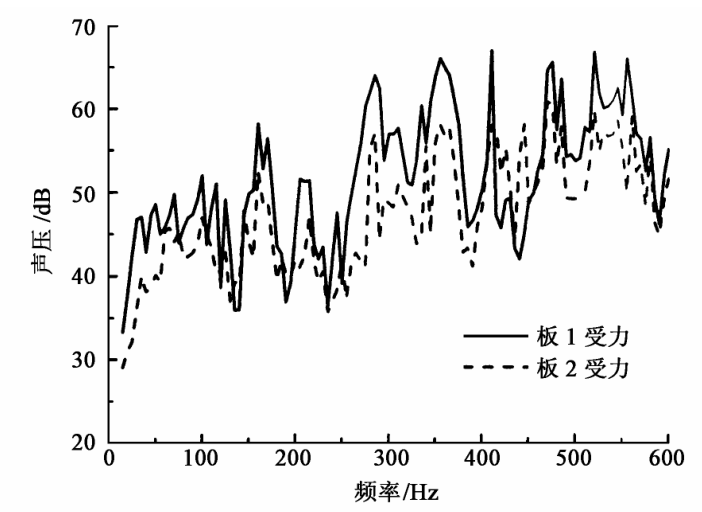
图 4 两板分别受力时点(5,4,3.8)的声压响应
Fig.4 Sound response of point (5,4,3.8) with the two plates subjected to a unit point load separately
《4 结论 》
4 结论
笔者建立了两个封闭弹性长方体连接结构的辐射声场模型。该模型考虑了两弹性长方体结构连接之间以及弹性板与腔体内声场之间的耦合。并通过算例分析了连接结构之间的耦合以及连接条件的改变对辐射声场影响。
1)在所分析频段内,间接力通过连接结构对弹性板 1 辐射声场的影响明显小于板 1 在同样直接力作用下的辐射声场。因此,当所要求分析的频率较低,间接力与直接力相当时,可以只考虑辐射面所受到的直接激励,而对于间接激励对声场的影响可以不予考虑。
2)连接结构的线弹簧刚度的变化对辐射声场的影响甚于旋转弹簧刚度的变化,且线弹簧刚度取值越大,辐射声场的声压强度愈大。因此,在控制结构的辐射声场时,改变线弹簧的刚度更加有效。














 京公网安备 11010502051620号
京公网安备 11010502051620号




