《1 前言》
1 前言
SPH 方法是计算力学领域新兴的一种无网格 Lagrangian 算法。SPH 方法基于插值原理,通过利用核估算式将一个偏微分方程转化为积分形式。这个积分方程在数值上通过一系列离散的质点(粒子)的总和来逼近。在 SPH 方法中,所有质点的整体运动都可以被看作是流体运动,构成流体动力学方程组的动量守恒、质量守恒、能量守恒方程都容易用力学和热力学语言来描述。由于计算中不需要网格,避免了大变形问题中网格重构,网格畸变等问题,使其计算精度不受结构变形程度的影响。这使得该方法在解决非线性动力学问题方面迅速发展,尤其近几年来,成为高速碰撞,靶板贯穿,连续体结构的解体、断裂,固体的层裂、脆性断裂等问题数值模拟中一种有吸引力和发展前景的新方法。
SPH 算法是 1977 年后发展起来的一种无网格方法,最早应用于天文学领域,由 Lucy,Gingold 和Monaghan 等人提出[1,2],用来解决天体物理中涉及流体质团无边界状态下在三维空间任意流动的问题。随后,Gingold,Monaghan 以及 Benz 等人对 SPH 进行了改进和完善,使其应用领域扩展到流体动力学[3]。尽管 SPH 具有诸如纯 Lagrangian、无网格以及简单等优点,但是在发展初期,由于计算精度、边界条件、激波间断等问题的影响,多年以来并没有引起计算力学领域研究者们的浓厚兴趣。令人惊讶的是,进入 20 世纪 90 年代,在许多领域都出现了大量的相关文献,例如固体的侵彻冲击、流体动力学、二相流、磁流体动力学,以及材料动载响应等[4]。国内关于 SPH 方法的最早论述始见于 1995 年岳宗五和贝新源发表的论文[5],1996 年张锁春在计算物理上也对 SPH 方法进行了综述[6]。近几年,国防科技大学、中国工程物理研究院、北京理工大学和中国科技大学相继开展了该方面的工作。根据已发表的文章来看,与国际相比,对于算法的研究仍处于初始发展阶段,国内主要方向集中在 SPH 在冲击动力学方面的应用研究[7~13]。
SPH 方法的快速发展是与算法的不断改进密切相关的。早期关于计算精度、边界条件和激波间断等问题影响了它在其他方面的应用。在 1983 年和1990 年 Monaghan 等人相继在 SPH 方程中引入人为粘性和人为热流,以解决模拟的流体中的激波间断问题[14]。目前,在方程中加入人为粘性项已成为普遍采用的技巧。对于边界处理,在早期应用 SPH 处理天文学问题时,人们并不在意边界的影响。但是随着 SPH 的不断推广应用,对于各种问题的边界处理引起广泛的重视。为了解决该技术难点, Johnson和 Beisssel 重构了核函数以改善应变的计算[15];Randles 和 Libersky 等人提出 “虚拟粒子” (ghost particles)的办法处理固壁边界[16];对于自由滑移固壁边界条件,Monaghan 提出用加排斥力(repulsive force)方法模拟了简单自由面的不可压缩流动,以防止出现实际粒子穿越固壁的反常现象[14]。从现在的情况看,边界处理问题仍然是 SPH 方法应用中的一个难点,尤其对于接触边界,包括同种介质和不同介质间的接触,处理起来十分困难。
从文献上看,目前国际上 SPH 方法的研究主要集中于以下两个方面。一是算法研究。由于该算法起步时间晚,在算法方面仍然不够完善,而且该方法以插值理论为基础,根据不同的核函数形式可以推导出不同形式的离散格式。为了改进算法,人们对不同的核函数及插值形式进行讨论,改进人为粘性项,改进边界问题的处理办法。二是 SPH 方法应用研究。随着方法的发展,SPH 应用领域早已从最初的天体物理转向更普遍的计算力学等方面[16]。目前,较为集中的方向包括流体流动和材料动态响应。美国在多年研究基础上开发出了 MAGI[17,18],SPHINX[19]等专用 SPH 代码,同时在一些已有的非线性动力学有限元代码如 LS -DYNA,CASTEM -PLEXUS[20],PRONTO[21]中加入 SPH 算法,使该方法得到了一定的应用推广。
总之,相比于历史悠久的有限元、有限差分等方法,SPH 具有一定优点,但同时还处于不断发展之中,算法需要不断完善,其应用也需要不断开发。
《2 SPH 方法基本原理》
2 SPH 方法基本原理
《2.1 离散质点插值》
2.1 离散质点插值
SPH 算法是一种无网格 Lagrange 算法,计算原理是将模拟对象离散为一组 SPH 质点,每个质点代表一个已知物理性质的插值点,通过使用核函数进行插值计算,可将微分形式的流体动力学守恒方程转化为积分方程,从而可以给出任意一点处场变量的“核估计”。在计算上,“核” 相当于一个加权函数,它决定了对一个位置 r 处的场变量有贡献的单个场变量的多少。在计算上,可将积分方程改写成只针对近邻粒子的求和形式。对于任意质点在空间 r 处的连续函数的值可以由以下核估算式求出:
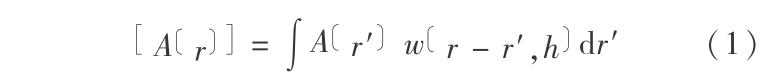
其中,h 为核函数的作用距离,称为光滑长度。这里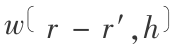 是具有以下特性的插值核并且
是具有以下特性的插值核并且

这里 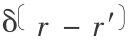 是 Dirac 函数。核函数满足一定的区域性,只在有限范围内有作用,如图 1 所示。显然,满足这样条件的插值核有许多种。在 SPH 方法中应用最广泛的核函数是三次 B 样条函数,通过文献看,主要的核函数还有 Gaussian 核函数、Super -Gaussian 核函数、指数核函数以及平方样条函数等。
是 Dirac 函数。核函数满足一定的区域性,只在有限范围内有作用,如图 1 所示。显然,满足这样条件的插值核有许多种。在 SPH 方法中应用最广泛的核函数是三次 B 样条函数,通过文献看,主要的核函数还有 Gaussian 核函数、Super -Gaussian 核函数、指数核函数以及平方样条函数等。
《图1》
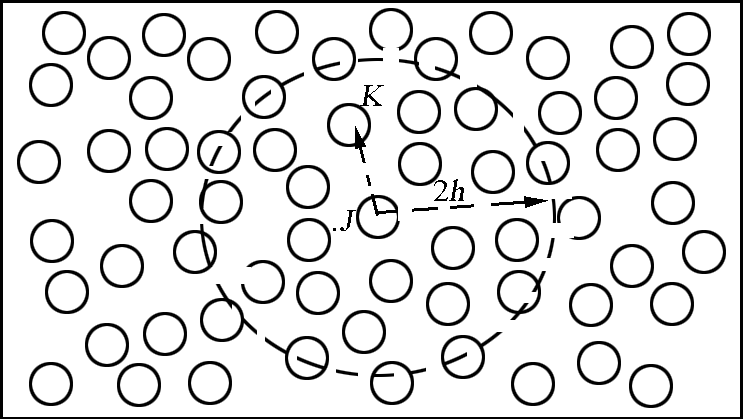
图1 质点 j 与距离 2 h 范围内的邻居质点相作用
Fig.1 SPH particle neighborhood
假定 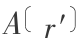 在 N 个离散点上已知,则它可以近似为
在 N 个离散点上已知,则它可以近似为

这里 (dV)k 是 rk 的微元体体积,如果 rk 的微元体质量为 mk ,平均密度为 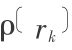 ,则(dV)k =
,则(dV)k = 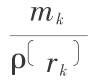 , 这时(1)式可以改写成如下求和形式
, 这时(1)式可以改写成如下求和形式
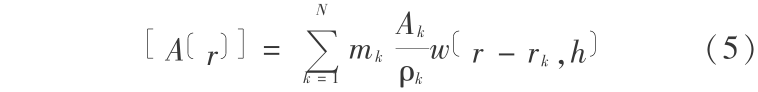
利用(5)式,通过分析函数 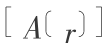 可以近似任何类型的场分布 A (如果 w 是 n 次可微的,
可以近似任何类型的场分布 A (如果 w 是 n 次可微的,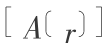 也是 n 次可微的)。密度的光滑形式为
也是 n 次可微的)。密度的光滑形式为
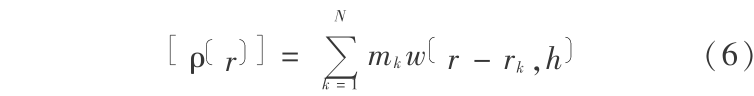
一个场量的光滑梯度

经分部积分,也可以参照从(1)推出(5)的类似方法得到
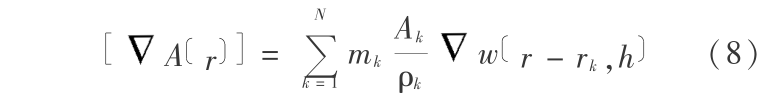
与求梯度类似,可以得到矢量散度的 SPH 表达式,如对于速度 v ,则有
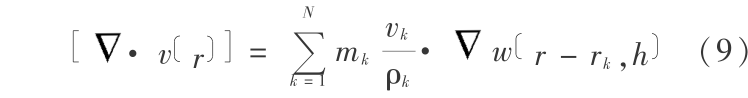
从式(5)、式(6)、式(7)、式(9)这些基本关系式可以看出,在 SPH 方法中场函数及其空间导数的计算,不需要借助网格,只取决于空间粒子的分布。
《2.2 SPH 算法控制方程》
2.2 SPH 算法控制方程
对于连续体力学的基本守恒方程组
质量守恒方程: 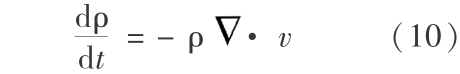
动量守恒方程: 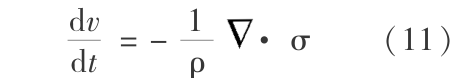
能量守恒方程: 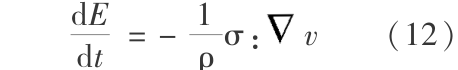
利用 2.1 节中得到的基本关系式就可以推导上述方程的 SPH 离散形式。它们的 SPH 形式如下。

《3 算例》
3 算例
《3.1 二维双杆对碰问题》
3.1 二维双杆对碰问题
尺寸为 30 mm ×10 mm 的对称铝杆以 100 m/s 的速度相对碰撞,用 SPH 方法模拟其变形情况,材料模型选用等向塑性硬化模型,材料参数见表 1。数值模拟中,杆件被均匀地离散为 5 400 个粒子单元,计算时间 20 μs。图 2 显示了各时刻其变形情况。图 3、图 4 分步显示了接触面位置节点位移和塑性应变随时间的变化历程。
《表1》
表1 材料参数
Table 1 Material parameters

《图2》
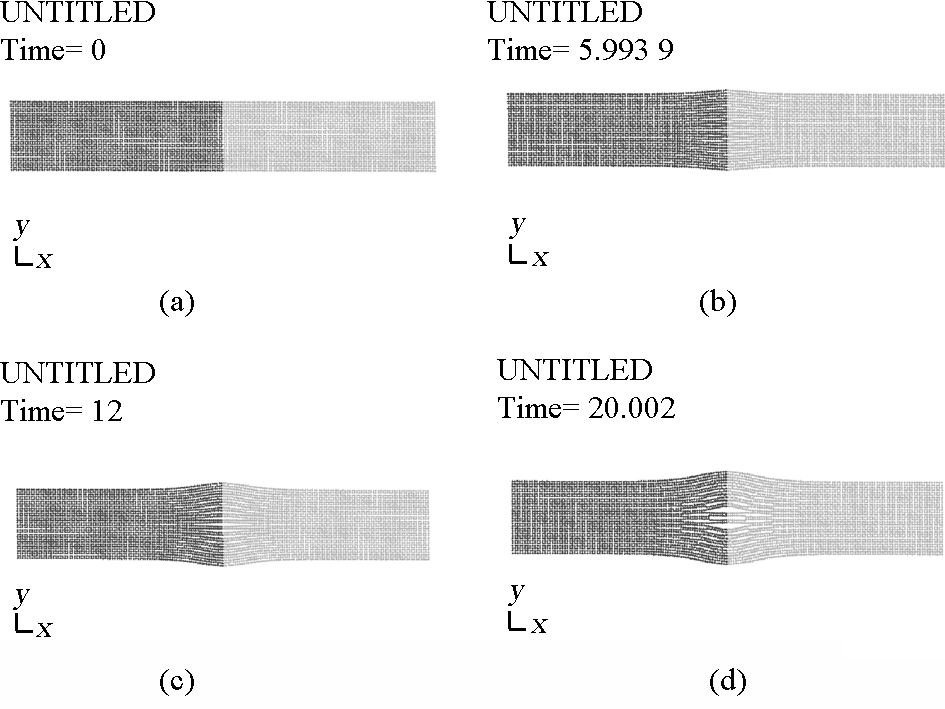
图2 铝杆在各不同时刻的变形图像
Fig.2 Impacting simulations for two Al bars
《图3》
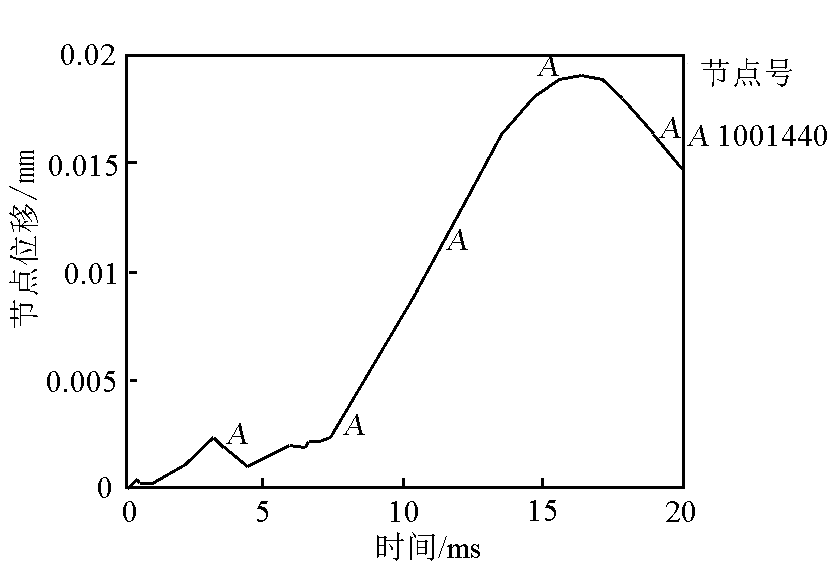
图3 接触面节点位移随时间的变化
Fig.3 Node displacement history on contact interface
《图4》

图4 接触面节点塑性应变随时间的变化
Fig.4 Node effective plastic strain history on contact interface
其中,ρ 是密度,E 是弹性模量,γ 是泊松比, σs 是屈服极限, ET 是切线模量。
《3.2 铝杆撞击固壁问题》
3.2 铝杆撞击固壁问题
尺寸 25 mm ×7.5 mm 的铝杆以速度 50 m/s 撞击固壁。材料模型选用塑性硬化模型,材料参数见表 2。数值模拟中,将结构均匀离散为 4 800 个粒子单元,计算时间 35 μs。图 5 显示了各时刻结构变形情况。
《表2》
表2 材料参数
Table 2 Material parameters

《图5》

图5 铝杆在各不同时刻的变形图像
Fig.5 Simulations for Al bar impacting on solid wall
《图6》
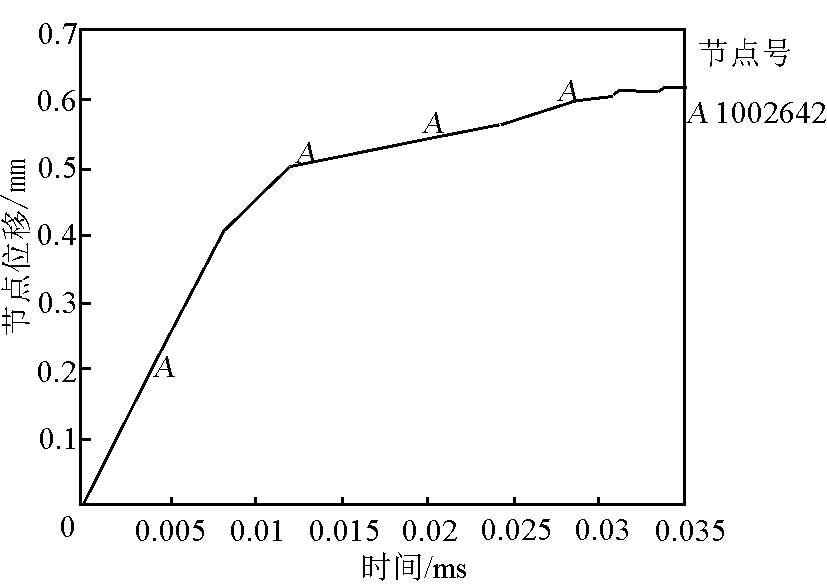
图6 接触面节点位移随时间的变化图
Fig.6 Node displacement history on contact interface
《图7》
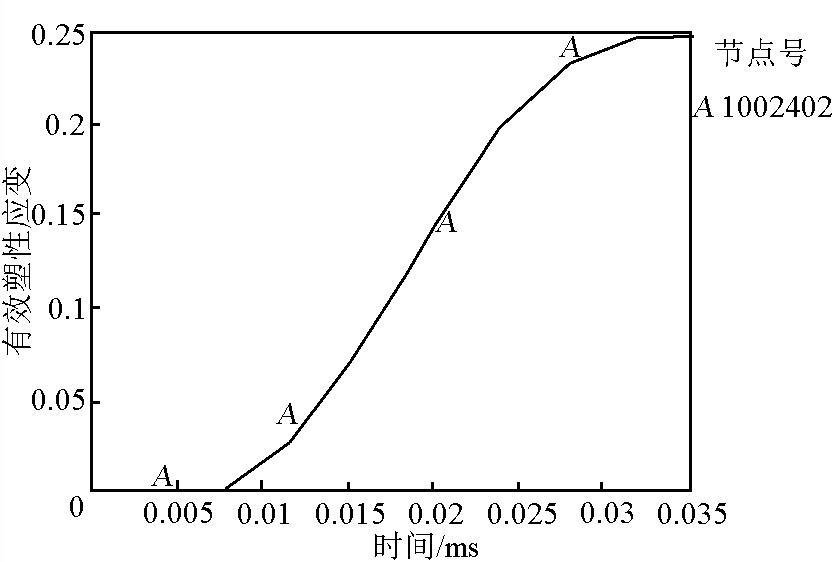
图7 接触面节点塑性应变随时间的变化
Fig.7 Node effective plastic strain history on contact interface
《4 热传导问题 SPH 模型初探》
4 热传导问题 SPH 模型初探
在许多问题的物理模型中都有热量传递的过程,这就有必要引入热传导方程。对于热传导问题的 SPH 模拟,国外做过少量的研究[22,23]。利用国外学者提出的方法,可以推导热传导问题的 SPH 离散格式。热传导的微分方程的形式为:

这里 κ 是导热系数。把这个热传导方程转化为 SPH 方程的一个最简单办法是直接对 T 插值,通过微分形成梯度,然后再微分一次形成散度。但是,实际过程中,由 SPH 近似得到的二阶导数估算值对质点的无秩序分布十分敏感。于是,探索一种对热传导方程的积分估值:
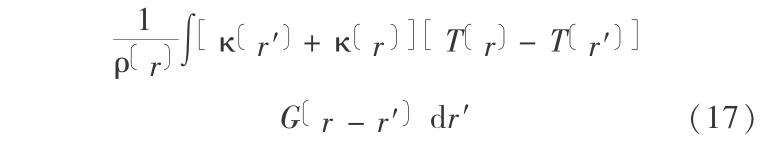
它的 SPH 表达式为
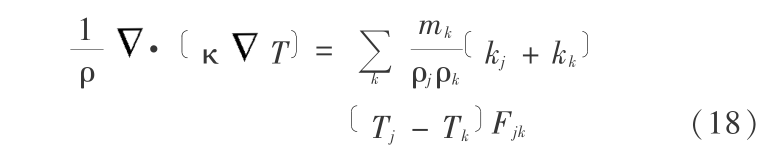
方程(16)的 SPH 形式为
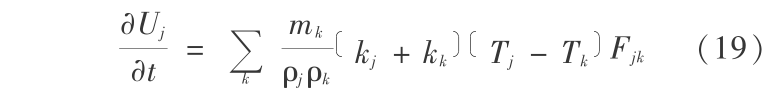














 京公网安备 11010502051620号
京公网安备 11010502051620号




