一种改进的Hilbert能量谱算法研究

摘要

分析了HHT中Hilbert能量谱的原理；研究了瞬时频率谱中端点效应产生的原因，将ARMA模型应用于Hilbert能量谱计算中，以旋转机械振动信号为对象，运用所提的方法对HHT中典型的本征模式函数进行仿真实验；通过与传统方法比较，证明它可以有效地改进端点效应，优化Hilbert能量谱。

正文

《1 前言》

1 前言

Hilbert-Huang变换 (简称HHT) 作为一种非平稳数据处理的新方法, 已经逐渐被人们所接受, 目前已广泛应用于海洋、地震、机械振动信号分析等领域 ^[1,2,3]。

然而, 在经验模式分解和Hilbert变换过程中, 都会出现端点效应, 严重影响HHT的分析精度。大量文献对经验模式分解的端点失真问题进行了研究并提出了解决方案 ^[4,5,6], 但是, 对Hilbert能量谱端点失真问题进行深入研究却寥寥无几。作为HHT的关键步骤之一, Hilbert能量谱的端点失真问题同样有待于深入解决。文献[5]提出了在信号的两端分别构造小波串以解决Hilbert谱端点失真的问题, 但未对所提出的方法进行解释和实验, 其效果没有说服力。文献[6]采用单层、单个神经元及线性神经网络对模态分量进行延长, 以消除端点效应, 但该方法存在网络训练不收敛的情况, 并且计算时间过长, 实用性不强, 未对Hilbert能量谱端点效应产生的原因进行深入分析。

在文献[4]中, 笔者所在的研究所对经验模式分解的端点效应进行了研究, 提出了可靠的改进方法;笔者对Hilbert变换的端点效应进行了研究, 分析了端点效应产生的原因, 将ARMA模型应用于Hilbert能量谱的计算中, 试图解决瞬时频率谱中端点“飞跃”的问题。

《2 Hilbert变换理论》

2 Hilbert变换理论

笔者针对HHT中机械振动信号通过经验模式分解以后获得的本征模式函数 (intrinsic mode function, IMF) 的Hilbert变换进行了研究。IMF是指对数据序列进行经验模式分解 (empirical mode decomposition, EMD) 之后得到的一组数据序列分量, 由于EMD方法认为信号是由不同尺度的“波动”分量构成的, 因此规定这个分量满足以下条件 ^[7]:

1) 在整个数据序列内, 过零点与极值点个数最多相差1;

2) 局部均值为零。

由以上两点可以看出, IMF是一个非单调的波动信号, 其上、下包络关于时间轴是对称的。

设x (t) 为实信号, 为了分析方便, 可以构造一个具有相同能量和相同频率的复信号q (t) , 并且x (t) 为q (t) 的实部。假设q (t) 的虚部为 $\hat{x}$ $\hat{x}$ (t) , 则q (t) 可以表示为

$q (t) = x (t) + j \hat{x} (t) (1)$ $q (t) = x (t) + j \hat{x} (t) (1)$

如果将q (t) 表示为极坐标的形式, 则

$q (t) = a (t) e^{j ϕ (t)} (2)$ $q (t) = a (t) e^{j ϕ (t)} (2)$

并且有

$\begin{array}{l} a (t) = \sqrt{x^{2} (t) + \hat{x}^{2} (t)} (3) \\ ϕ (t) = \arctan {\frac{\hat{x} (t)}{x (t)}} (4) \end{array}$ $\begin{array}{l} a (t) = \sqrt{x^{2} (t) + \hat{x}^{2} (t)} (3) \\ ϕ (t) = \arctan {\frac{\hat{x} (t)}{x (t)}} (4) \end{array}$

式 (3) 称复信号q (t) 的瞬时幅值, 代表信号的瞬时能量;ϕ (t) 称为信号的瞬时相位, ϕ (t) 的变化率代表信号的瞬时频率 ^[8], 即

$f (t) = \frac{1}{2 π} \frac{d ϕ (t)}{d t} (5)$ $f (t) = \frac{1}{2 π} \frac{d ϕ (t)}{d t} (5)$

设实信号x (t) 的频谱为S (f) , 复信号q (t) 的频谱为Q (f) , 则根据以上假设条件, 同时考虑到实信号的频谱为对称频率;只保留正频率, 并且将幅值加倍, 保持信号的能量不变, 则有

$Q (f) = {\begin{cases} 2 S (f), f > 0 \\ S (f), f = 0 \\ 0, f < 0 \end{cases} (6)$ $Q (f) = {\begin{cases} 2 S (f), f > 0 \\ S (f), f = 0 \\ 0, f < 0 \end{cases} (6)$

由式 (6) 可以看出, Q (f) 可以通过S (f) 滤波得到, 滤波函数H (f) 可以表示为

$Η (f) = {\begin{cases} 1, f > 0 \\ 0, f = 0 \\ - 1, f < 0 \end{cases} (7)$ $Η (f) = {\begin{cases} 1, f > 0 \\ 0, f = 0 \\ - 1, f < 0 \end{cases} (7)$

设式 (7) 对应的传递函数为h (t) , 则q (t) 可以表示为

$q (t) = x (t) + j x (t) * h (t) (8)$ $q (t) = x (t) + j x (t) * h (t) (8)$

由式 (8) 可以看到, q (t) 的虚部可以通过x (t) 与h (t) 的卷积得到;由实信号构造复信号虚部的过程称为Hilbert变换 (Hilbert transform, HT) , 如式 (9) 所示:

$\hat{x} (t) = \frac{1}{π} Ρ \int_{- \infty}^{+ \infty} \frac{x (τ)}{t - τ} d τ (9)$ $\hat{x} (t) = \frac{1}{π} Ρ \int_{- \infty}^{+ \infty} \frac{x (τ)}{t - τ} d τ (9)$

在式 (9) 的被积函数中, 由于存在极值点而不能直接积分, 因此引入了柯西主元P。Hilbert变换过程的推导, 还可以从相移±π/2的角度考查。

《3 端点问题的提出与分析》

3 端点问题的提出与分析

《3.1应用Hilbert变换分析信号瞬时参数》

3.1应用Hilbert变换分析信号瞬时参数

由式 (3) 、式 (4) 可知, 通过构造复信号的虚部, 可以获得信号的瞬时幅值和瞬时频率, 以下考查一个正弦信号 (符合IMF的定义) :

$x (t) = \sin (2 π f t) (10)$ $x (t) = \sin (2 π f t) (10)$

其中f=35 Hz, 设x (t) 的单位为mm;用Hilbert变换做出复信号的虚部, 其时域波形如图1所示。

《图1》

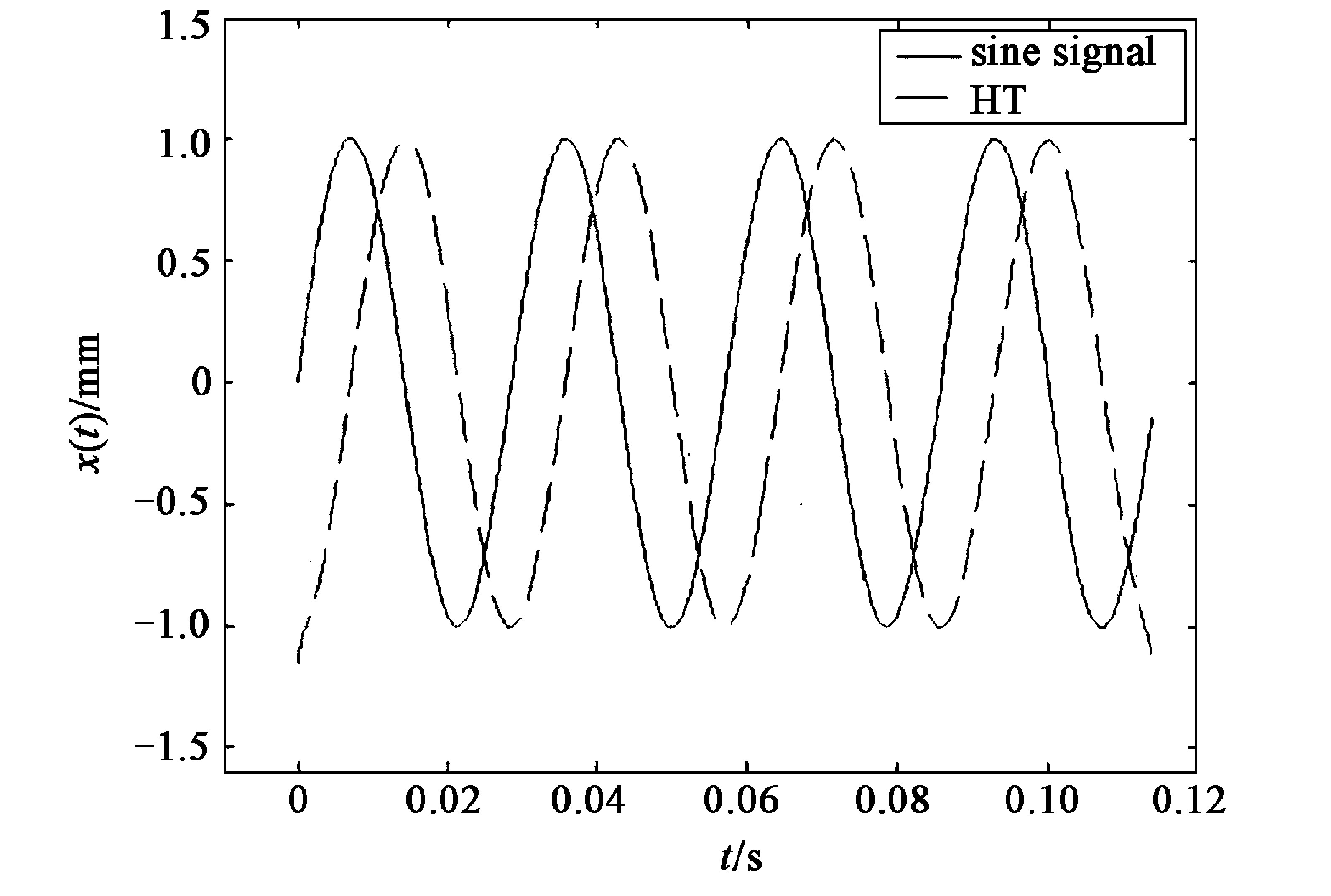
图1 正弦信号 (实线) 和Hilbert变换 (虚线)

Fig.1 Sine signal (solid line) and its Hilbert transform (dashed line)

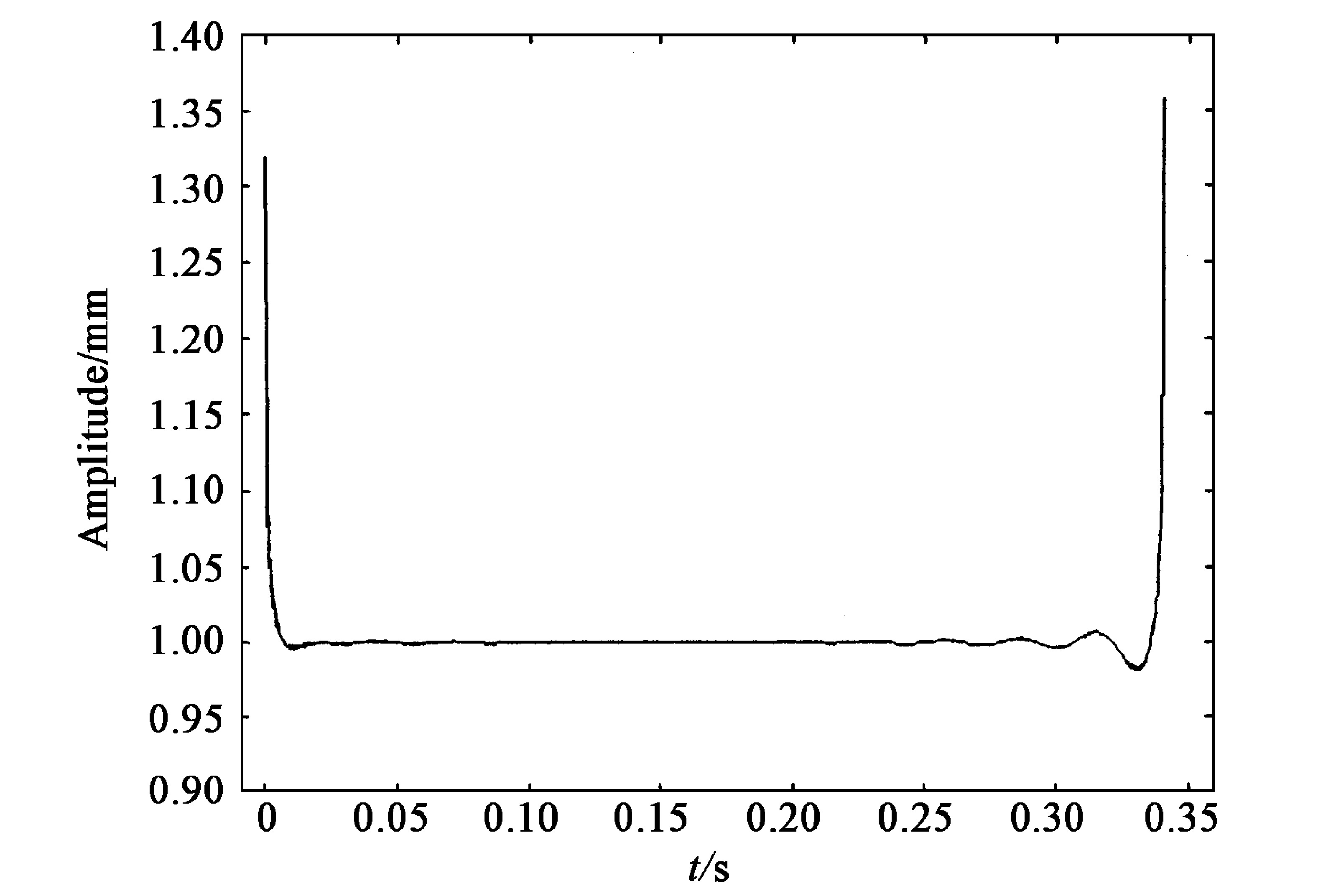
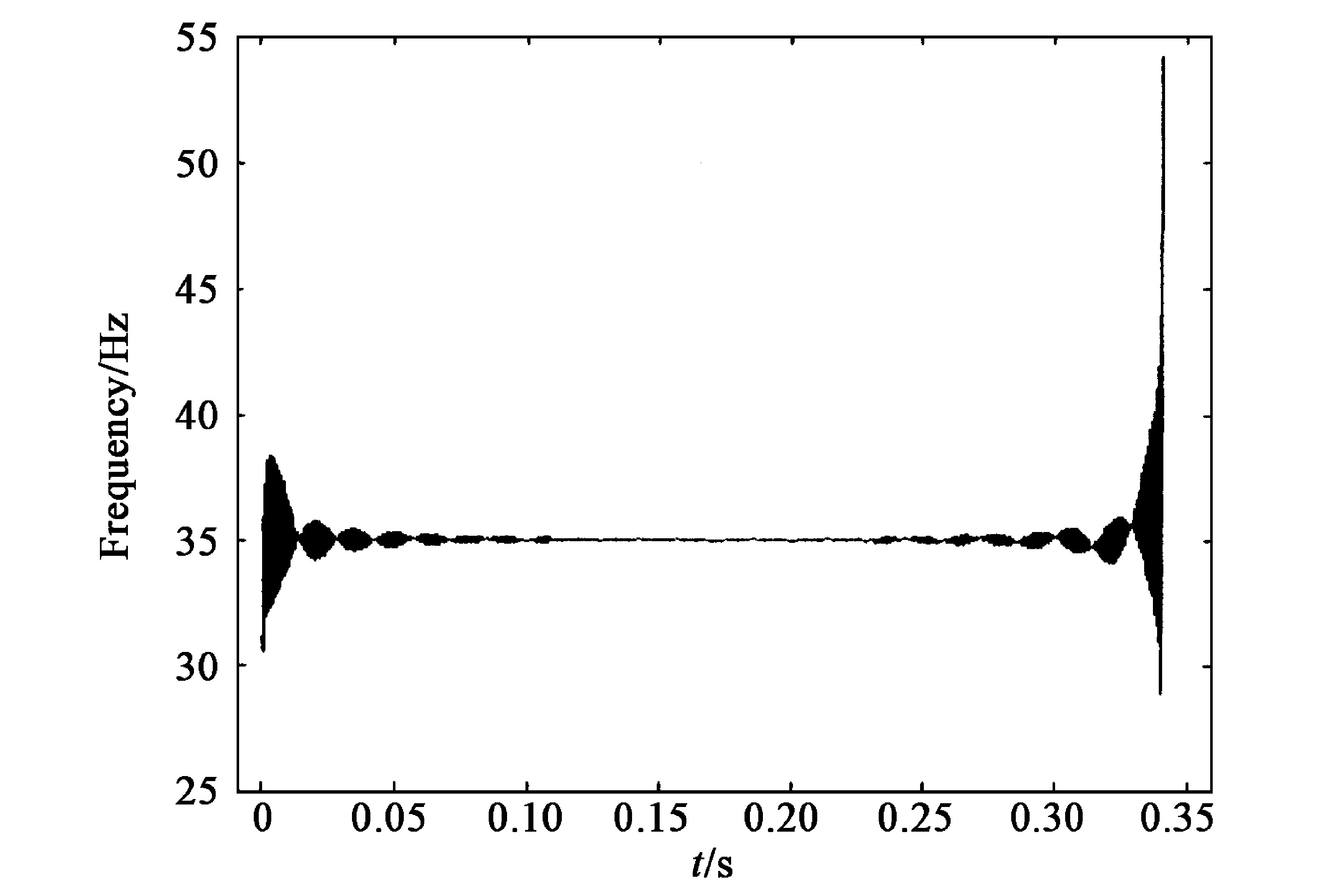
正弦信号的理想Hilbert变换应为与给出的正弦信号相位差π/2的正弦信号, 然而在图1中看到正弦信号的Hilbert变换信号 (虚线) 出现了明显的失真 (主要在两端) ;图2、图3分别给出了应用HT获得的信号的瞬时幅值和瞬时频率 (瞬时频率的计算采用前向插值法) ;对于式 (10) , 正确的瞬时幅值应恒等于1 mm, 而瞬时频率应恒等于35 Hz;由图2、图3看到, 通过HT得到正弦信号的瞬时参数基本上是正确的, 但在图形的两端出现了严重的失真 (飞跃和波动) 。

《图2》

图2 正弦信号的瞬时幅值谱

Fig.2 The instantaneous amplitude spectrum of sine signal

《图3》

图3 正弦信号的瞬时频率谱

Fig.3 The instantaneous frequency spectrum of sine signal

《3.2端点失真问题分析》

3.2端点失真问题分析

为了研究HT端点失真的原因, 对图4 Hilbert变换的推导过程进行分析 ^[9]:

《图4》

图4 Hilbert变换计算过程Fig.4 The calculating course of Hilbert transform

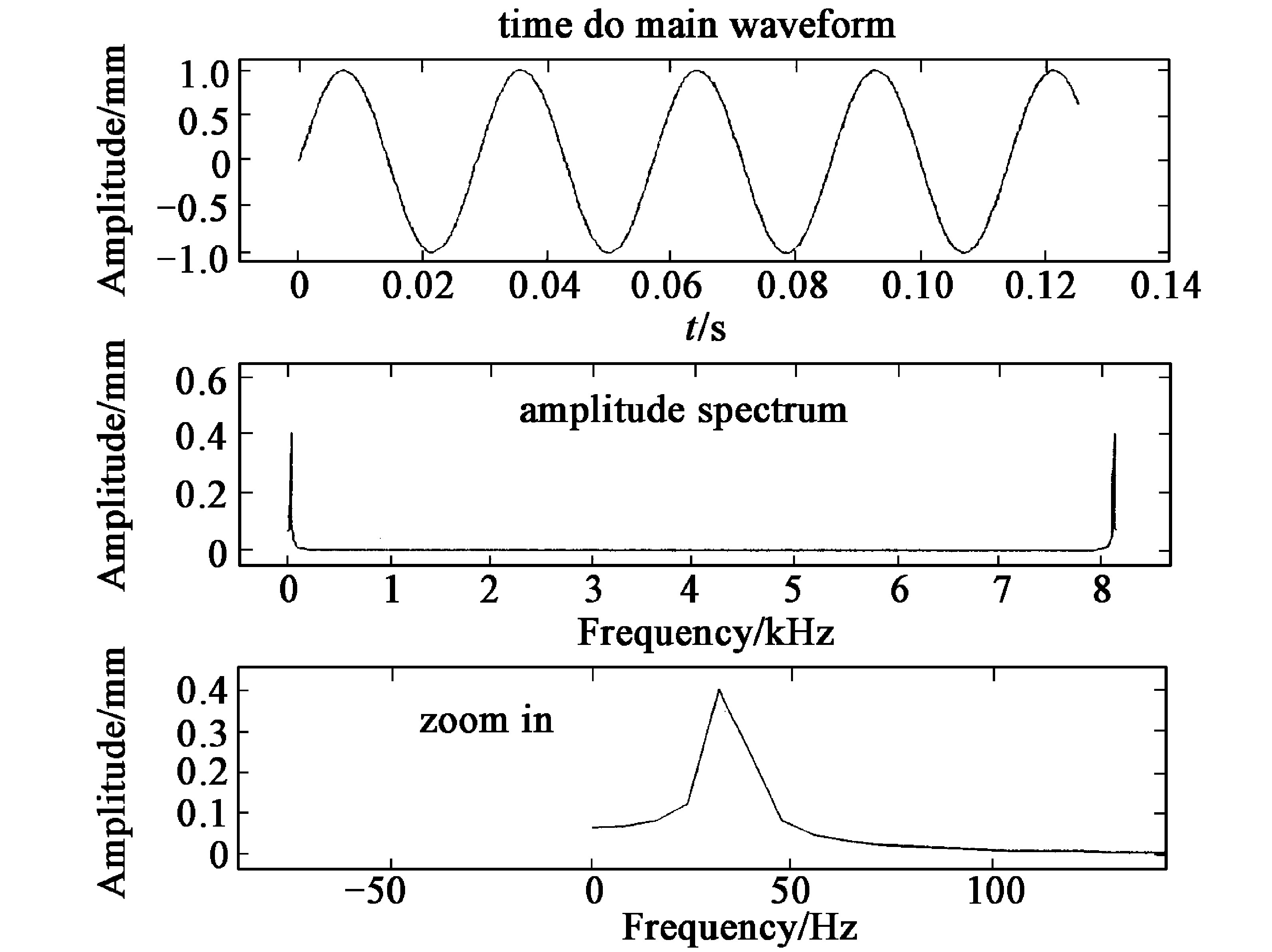
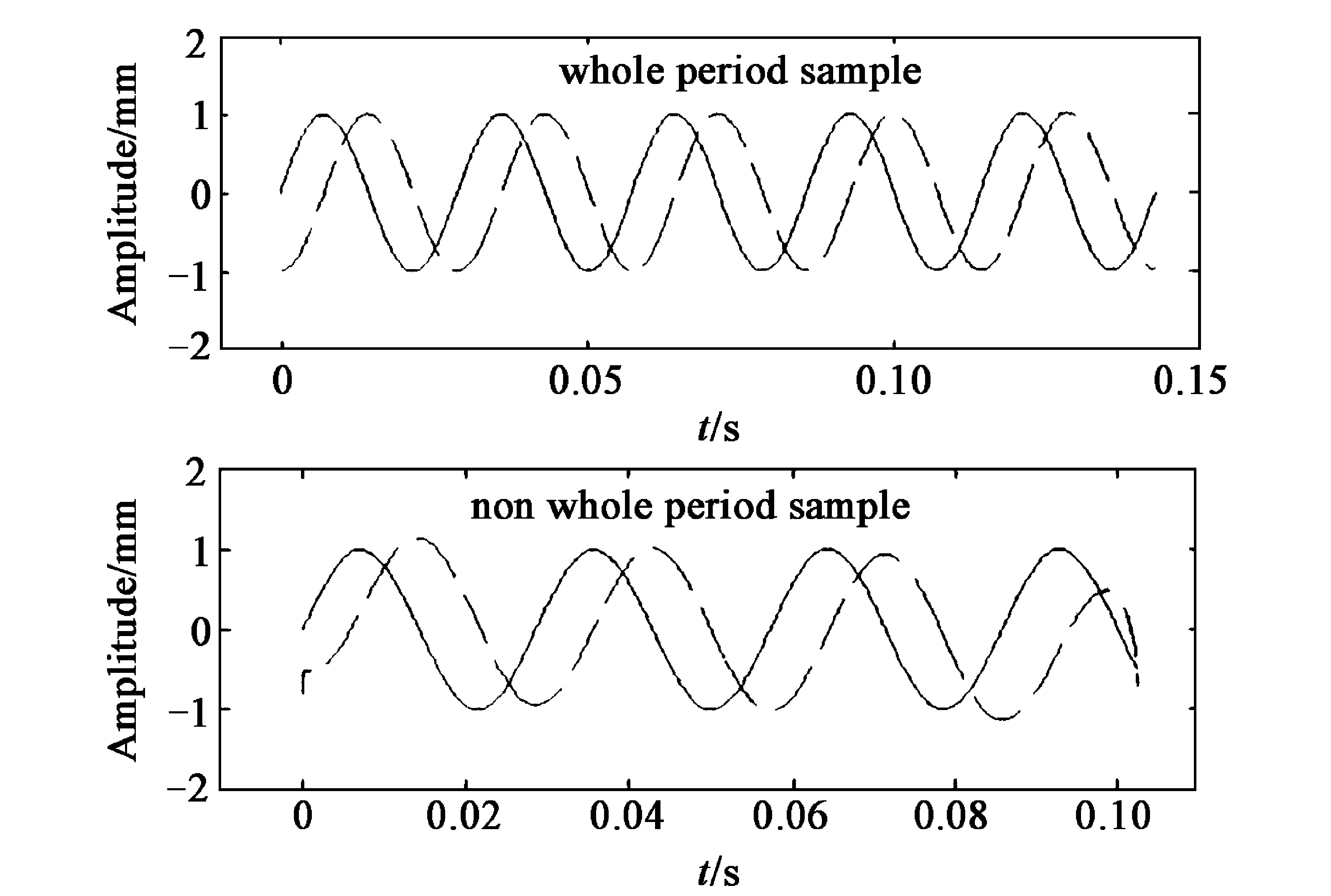
图4的第1步是将信号进行Fourier变换, 然而Fourier变换是将有限长序列作为周期序列的一个周期进行计算的, 因此, 当数据序列为非整周期采样时, 势必引入误差, 对变换后得到的频率产生影响;图5、图6是对式 (10) 进行整周期采样和非整周期采样的时域波形和幅值谱。对比可以看到整周期采样和非整周期采样频谱是有差别的。在非整周期采样中, 幅值谱有轻微的失真, 表现在35 Hz的谱线幅值小于0.5 mm, 从能量守恒的角度分析, 频谱中已混入其他成分, 然而, 由于实信号为双边谱, 直接对其FT进行IFT时, 这些误差恰好能够抵消, 从而得到正确的时域波形 ^[6]。

《图5》

图5 整周期采样及幅值谱图

Fig.5 The whole periodical sampling signal and its amplitude spectrum

《图6》

图6 非整周期采样及幅值谱图

Fig.6 The non-whole periodical sampling signal and its amplitude spectrum

图4中的第3、第4步, 即去掉 (双边谱的) 一边频谱, 并将幅值加倍。由以上分析可知, 在非整周期采样时, 由于频谱存在误差, 去掉一边频谱以后, 误差将无法抵消, 反映在HT信号的波形上, 表现为波形失真, 特别是反映在波形的两端。图7给出了式 (10) 整周期采样和非整周期采样的HT变换的波形。当整周期采样时, 由于FT变换基本上没有误差, 因此通过HT获得的余弦波形基本正确;而在非整周期采样时, 则出现了波形失真, 特别是在余弦信号的两端比较严重。

《图7》

图7 整/非整周期采样的HT波形

Fig.7 The HT waveform of whole and non-whole sampling signal

《4 Hilbert变换的改进算法》

4 Hilbert变换的改进算法

从第3章的分析可知, HT会产生误差, 并且误差主要分布在变换信号的两端。为此, 笔者提出以下改进算法:

1) 建立数据的ARMA模型, 并对其左、右进行延长, 获得新数据;

2) 求新数据的Hilbert变换;

3) 截取新数据的Hilbert变换, 获得原信号的HT。

由于Hilbert变换可以视为原信号进行±π/2相移得到的数据, 因此在Hilbert变换中, 任意截取一部分都应该仍为对应信号的Hilbert变换;同时, 由于变换过程中产生的误差主要集中在信号的两端, 因此, 通过舍弃两端数据获得的信号得到了极大改善。

调幅和调频是旋转机械常见的故障信号形式, 以下对这两种信号进行仿真实验 (实验中采用最大商谱算法, 模型阶数为30) :

· 调幅信号

$设 f (t) = (1 + 0.5 \sin (2 π f_{1} t)) \sin (2 π f_{0} t) (11)$ $设 f (t) = (1 + 0.5 \sin (2 π f_{1} t)) \sin (2 π f_{0} t) (11)$

《图8》

图8 调幅信号、延长信号及HT包络

Fig.8 The amplitude-modulated signal and its lengthened signal with HT envelope

式中f₁=7 Hz, f₀=100 Hz。

图8为式 (11) 及通过ARMA建模延长后的波形及HT包络。由图8看到, 原信号及延长信号的两端通过HT获得的包络都产生了失真, 然而延长信号中原信号部分的包络却很好。图9为原方法和改进后方法获得的调幅信号瞬时频率图。由图9看到, 改进后获得的瞬时频率基本上为调幅信号的载波频率, 端点的失真也被正确消除。

《图9》

图9 调幅信号改进前与改进后瞬时频率谱

Fig.9 The instantaneous frequency spectrum of amplitude-modulated signal before and after improved

· 调频信号

$设 f (t) = \sin (2 π f_{0} t + \sin (2 π f_{1} t)) (12)$ $设 f (t) = \sin (2 π f_{0} t + \sin (2 π f_{1} t)) (12)$

式中f₁=7 Hz, f₀=100 Hz。

图10为式 (12) 及通过ARMA建模延长后的波形及HT包络;图11为使用传统方法与使用改进后方法获得的瞬时频谱图, 两种方法均获得很好的效果。

《图10》

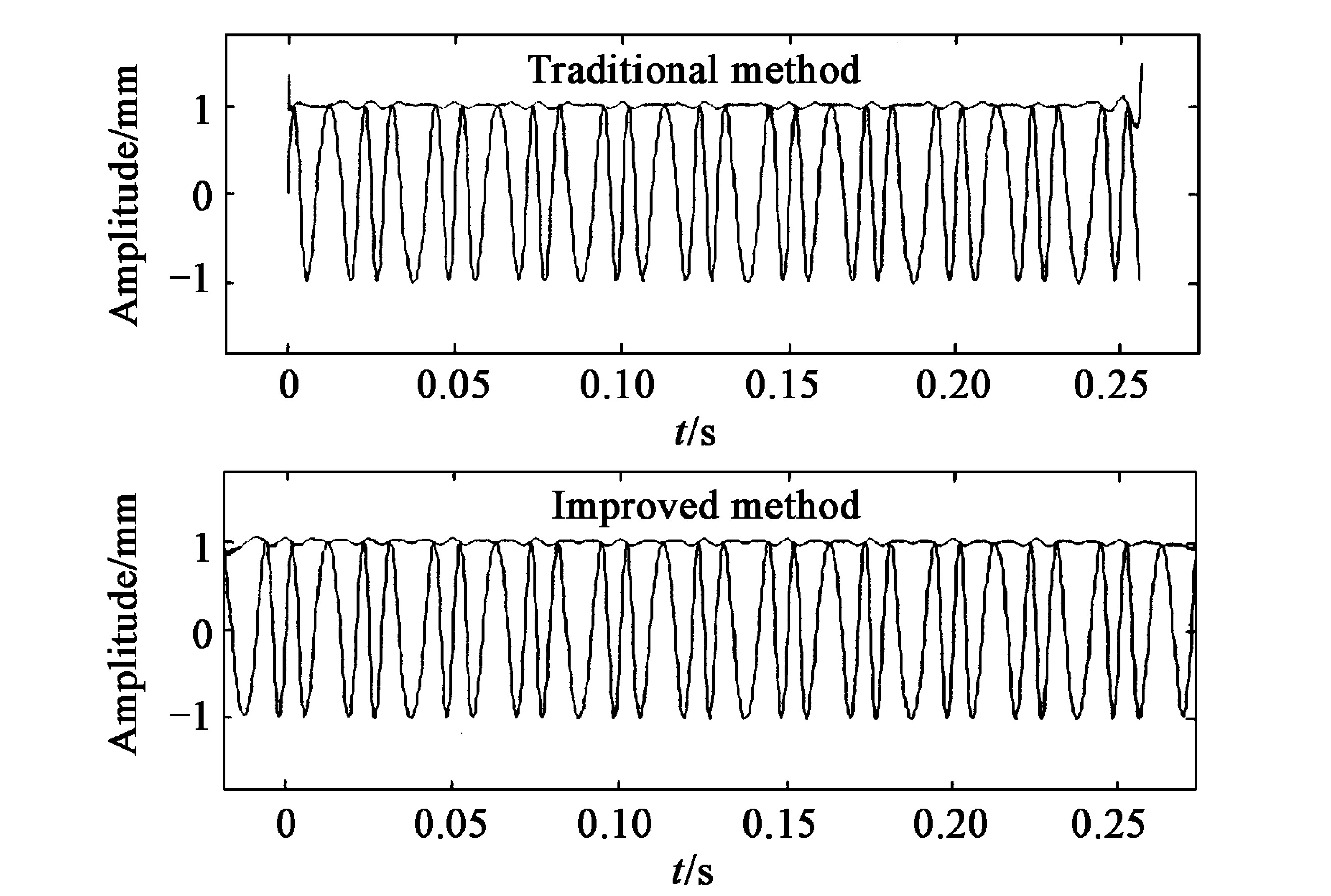
图10 调频信号、延长信号及包络

Fig.10 The frequency-modulated signal and its lengthened signal with HT envelope

《图11》

图11 调频信号改进前与改进后瞬时频率谱

Fig.11 The instantaneous frequency spectrum of frequency-modulated signal before and after improved

《5 结论》

5 结论

笔者简单介绍了Hilbert变换, 分析了Hilbert变换产生误差的原因在于Fourier变换过程中的误差;针对经验模式分解的本征模式函数, 提出应用ARMA建模对数据进行延长, 从而消除端点效应, 有效地解决了Hilbert能量谱的端点效应及波形失真。

展示更多