《1　前言》

1　前言

离群数据（outlier）就是明显偏离其他数据，不满足数据的一般模式或行为，与存在的其他数据不一致的数据[1]。离群数据挖掘是从大量复杂的数据集中发现存在于小部分异常数据中的新颖的、与常规数据模式显著不同的新的数据模式。与统计学中的离群值稍有不同，统计学中的离群值往往指的是一维的数据，而要研究的数据是高维的。高维空间数据分布稀疏，使数据之间的距离尺度及以此为基础的区域密度不再具有直观意义。从一个数据点来看，其他点到它的距离落在一个很小的区间内，很难给出一个合适的近似度阈值来确定哪些点与之相似[2]。另外，在实际使用时数据维数往往很高，而对高维数据的估计需要的样本个数与维数构成指数增长的关系，称维数灾难（curse of dimensionality）。为了解决这一问题，一些新的研究开始将高维空间的数据投影到子空间以后再进行离群点检测。例如，美国 IBM 公司的研究员 Aggarwal 等采用演化计算方式寻找所有投影到子空间稀疏的小方格，将其中的数据作为离群点[3]。将数据投影到子空间再进行数据挖掘是可行的但这带来了另一个问题———由于在实际使用中，样本点是非常稀少的，而随着数据维数的增加，对维度进行组合得到的子空间个数呈指数级增长。对此不可能采用穷举法，因为这样的计算代价太大。另外，大量的数据分析问题本质上是非线性的，甚至是高度的非线性，直接投影到子空间进行计算将不能很好地发现离群点。核函数在支持向量机（SVM）中起着很重要的作用，它是解决非线性问题及克服维数灾难问题的关键。支持向量机算法在于不直接计算复杂的非线性变换，而是计算非线性变换的点积，即核函数，从而大大简化了计算。笔者提出的算法基本思想是：提出非线性数据变换通用数学模型，并将非线性问题转化为高维特征空间中的线性问题，作为非线性变换的一个特例，将其与核函数有机融合，然后利用该融合进行维数约减，对所得数据对象每个投影分量逐个判断数据点是否是离群点。

《2　基于非线性数据变换的离群点检测算法》

2　基于非线性数据变换的离群点检测算法

《2.1　非线性数据变换通用模型》

2.1　非线性数据变换通用模型

对大规模、高维度的数据集合进行离群数据挖掘通常需要耗费大量的时间和人力、物力，并且这种任务常常变得不现实和不能切实可行，尤其是在交互式离群数据挖掘的情况下。在低维情况下，这些任务能够很顺利的进行，但并不能很好地推广到高维情况中去，特别是在样本函数和参数估计时，要保持一定的准确度，需要的数据量通常会随着维数的增加而呈几何指数增长。解决高维度问题的一个简单方法就是数据变换法[4]。基于这一数学思想，当采取某种控制策略，选取 p ′ 个投影方向，就可以将 p 个原始输入变量变换为 p ′ 个变量集合，采用一个非线性数据变换给出下面通用模型。

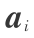设有 n 行 p 列原始输入数据矩阵 X，即为 n 个数据向量，p 个变量，其中 Xi （ i = 1， 2， …， p ′）表示第 i 个向量数据列； 是 p 行 p ′ 列的线性变换矩阵，这里的列代表一个投影方向，用 （i = 1， 2，…， p ′）表示第 i  个投影方向；G = ｛gi （i = 1， 2，…， p ′｝ 为一组非线性变换函数；F = （F1 F2 … Fip）是原始输入数据矩阵 X  经过   线性变换后具有 p ′ 个变量的输出数据矩阵；H =（H1 H2 … Hp）是 F  经过非线性变换函数 G  处理后的最后输出数据矩阵。则：

因此，原始输入数据矩阵 X  经过 线性变换和 G 非线性变换得到一个通用非线性数据变换模型，可表示为 H  = G（Xa ）。其中   和 G  的选取在不同情况下，可根据不同的要求，采用不同的选取控制策略。现有的多元统计方法和数据分析方法可借鉴。

《2.2　非线性数据变换特例及维数约减的应用》

2.2　非线性数据变换特例及维数约减的应用

主成分分析是把多个相关的原始变量转换成少数几个独立的变量，进而反映多个变量的独立综合指标。主成分按照数据样本点在某 k 维空间上投影的差异平方和比其他空间投影时更小为原则选取投影方向和投影个数，所得个数等于原指标的个数，只是一般仅取少数几个主成分作综合指标。其目标是为了得到数据最大变化量，并降低数据集合的维数。

将 n 行 p 列原始输入数据矩阵 X  标准化（这样可以消除变量量纲的影响），即以数据矩阵 X  的均值为中心，将每个变量的值与样本均值相减得到的偏差来表示。利用线性变换矩阵 做 X  的线性组合得到如下形式：

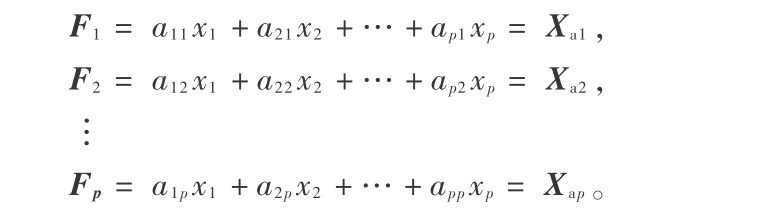
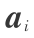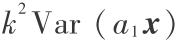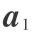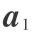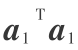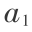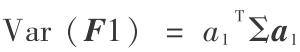其中，  为当 X  沿其方向投影时产生最大方差的 p × 1 列向量，Fi  是 X  中所有数据向量沿 方向的一切线性组合中方差最大的，且 Fi  与 Fj （i  ≠ j， i，j = 1， 2， …， p）不相关。由于对任意的常数 k，有 = ，所以如果不对 加以限制，就会使问题变得毫无意义。于是将限制 为单位向量，即 = 1，在此约束条件下寻求向量 ，使得 达到最大。

一般主成分分析是通过求数据矩阵 X 的特征向量和相应的特征值，并根据特征值的大小通过特征向量的线性组合得到数据的主成分。即 = = 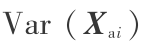 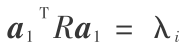。其中，R =X TX。引用一个平滑而连续的高斯核函数作为非线性变换函数 G（x）[4~6]，G（x）= G（xi ）G（xj ）。将所得主成分 Fi  经过非线性变换函数 G  处理等价于将 Fi  投影到高维特征空间中，则投影量为 Hi  = g（xi ） = mG（xi 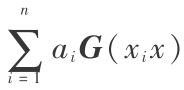） = ，式中 m  为数据在特征空间中的特征向量。

《2.3　算法描述》

2.3　算法描述

定义1　离群数据 T 。对于数据集 D =｛t1 ， t2 ，…， tn ｝，T  为数据对象，如果数据集中有 p  部分数据 S  远离于对象 T，S ∈ T， s ∈ S，则称 T 为离群数据。

定义 2　数据集 D。N  为数据对象数目，L 为对象的投影分量个数，对象 t  的 i  投影分量为离群投影分量，其定义：以对象 t  的投影分量 i  为中心，d  为邻域半径，邻域内所包含的数据对象最大个数 k，k ＜＜N 且 k  为输入的离群投影分量参数，当对象 t  的 i  投影分量的 d  邻域所包含的数据对象数目大于 k  时，对象 t  的 i  投影分量就为非离群投影分量。其中包含在 d  邻域内的数据对象 q 满足 q ∈ D 且 F（t， q）d， F（t， q）为对象 q 的 i 投影分量和对象 t 的 i 投影分量的分量距离函数。邻域半径 d 的数值等于数据集 D 中除去数据对象 t 的所有数据对象的 i 投影分量值的平均，它是由算法自动计算的一个参数。

定理　如果 S 集中任意点 s 是离群数据，S ∈ D，s ∈ S， q 与其第 k + 1 个最邻点距离小于 s 点与其第 k + 1 个最近邻点距离，q 不是离群数据。

证明：采用反证法。如果 q 是离群数据，k + 1 最邻近点与 q 点距离 F（k + 1， q） ＞d，又 s 点与 k + 1 邻近点距离 F（k + 1， s）d 与条件矛盾，命题得证。

定义 3　设数据集 D，离群领域所包含的对象数 M，数据对象数目 N，则 k =M/N 为该数据集的离群数据检测度。

定义 4　设数据样本集有两个投影分量，其大小为数据集 D 中的对象数目，当对象 t 的 i 投影分量为离群时，就将数据样本集的相应元素的值置为离群标记值，例如“0”代表正常，“1”代表离群。

基于以上定义与定理，建立基于非线性数据变换的离群点检测算法：

Step 1　对输入数据进行初步统计整理，将输入数据矩阵标准化：因为变量可能具有不同的量纲，因此计算前最好标准化所有数据；

Step 2　建立变量的相关矩阵：R =（1/n）X T X；

Step 3　求 R  的特征值，并计算投影输出数据矩阵 F；

Step 4　通过非线性数据变换进行维数约减得到投影分量 H（x）；

Step 5　对离群标记数据样本集和离群数据计数变量进行初始化；

Step 6　对数据对象的投影分量循环，遍历数据对象的投影分量，按照投影分量对数据对象逐个进行离群值判断；

Step 7　遍历数据对象，从而对数据样本集中数据对象在指定投影分量上的离群情况进行检测，并根据检测结果对离群标记数据样本集赋值；

Step 8　根据离群标记数据样本集的值，输出离群数据。

在算法遍历对象时，首先判断该对象是否已被置为离群，若是，则跳过该对象，否则，判断该对象在指定投影分量上是否为离群。算法中离群数据检测度参数由相关技术人员输入，可以输入具体数目，这时算法根据离群数据检测度公式 M =kN 自动计算出 M 的值。

《3　算法的实现及其实验结果的评估》

3　算法的实现及其实验结果的评估

测试数据集信息采用基于网络的安全审计数据，数据来源于美国国防部高级研究计划署（PARDA）1998 年，由麻省理工学院 Lincoln 实验室提供的用于入侵检测系统评估的常用数据集 KDDCup 1999 数据集[7]。它由 4 900 000 个训练实例构成，每个训练实例都是从原始网络连接数据中提取的属性分量。每个网络连接数据都是从某个 IP 地址发出的一系列 TCP 数据包，并且每个网络连接记录，都标为正常或者是入侵。而提取的属性向量包括一些基本特征，如网络连接的持续时间，协议类型，所传送的字节数目，表示这个连接是否异常的标志位，等等。还有一些通过其他手段获得的特征，如所执行的新建文件的次数，登录失败的次数，是不是获得管理员权限等。另外还有一些计算所获得的特征信息，如过去两秒钟内和当前连接到同一主机的连接数，在这些连接中居于“SYN”和“REJ”错误的比例，以及过去两秒钟和当前连接请求相同服务的连接数等。这个特征向量具有 42 个属性，数据集中入侵类型按攻击手段类型可划分为以下 4 类，包括：拒绝服务攻击（DOS），如 TCP 同步报文洪泛攻击；远程权限获取（R2L） ，如猜测口令；各种权限提升（U2R），如缓冲区溢出；各种端口扫描和漏洞扫描（Probe）。由于原始数据集过于庞大，且分布不均匀，实验使用其中的部分数据，并对非数值属性值做了预处理，经过预处理构成实验数据集，其为高维空间的数据点，数据集中所包含的各种攻击数量见图 1。

《图1》

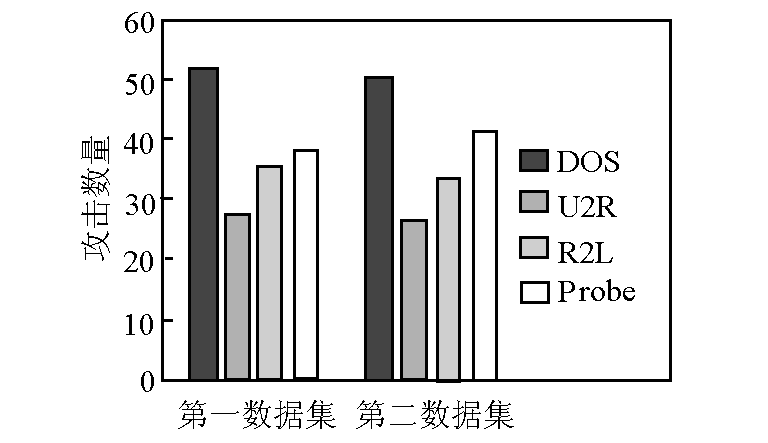
图1　数据集中各种攻击类型的数量

Fig.1　The amount of different aggressive type from dataset

基于非线性数据变换的离群点检测算法，首先由非线性数据变换进行维数约减，获得包括离群点的二维平面样本数据。实验 1 是针对包括离群点的线性可分样本数据集；实验 2 是针对包括离群点的线性不可分样本数据集，见图 2 和图 3。对于线性可分数据集，在高维数据集中发现离群点仍然是一个非常耗时的过程，但经过基于非线性数据变换的离群点检测算法将高维数据集转化为适合分析的小数据集以后，可将问题简化，从表 1 实验结果可以看出，在客观发现的方法中，算法将根据数据点的分布情况，自动地发现离群点。

《图2》

图2　线性可分的样本数据集的离群点检测结果

Fig.2　Result of outliers detection on linear separable dataset

《图3》

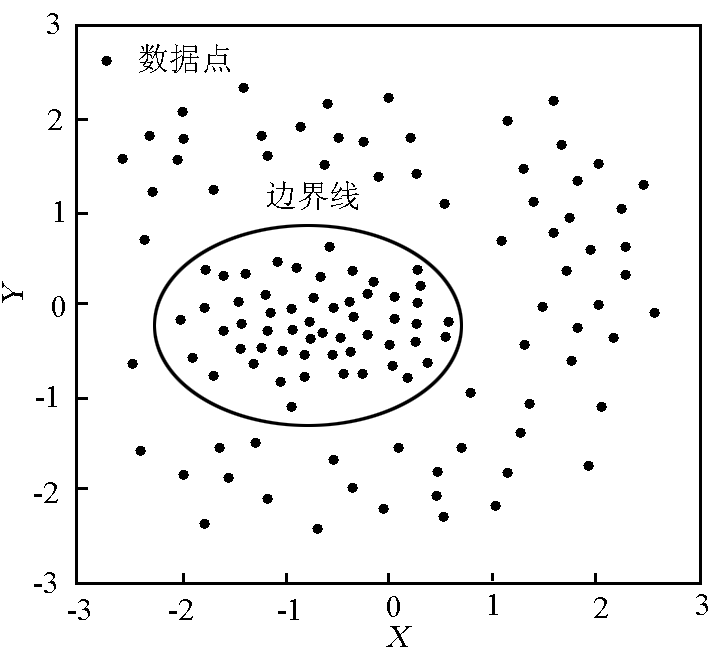
图3　线性不可分样本数据集的离群点检测结果

Fig.3　Result of outliers detection on nonlinear separable dataset

《表1》

表1　基于非线性数据变换的离群点检测算法实验结果

Table 1　Experimental result of outliers detection based on nonlinear data transformation

实验 2 中，一个线性不可分的数据样本集被用来测试算法的性能，表 1 显示了该数据样本集的检测结果，可以看出，对于线性不可分的数据样本集，适用于线性可分样本数据集的算法将要失败，当使用基于非线性数据变换的离群点检测算法就能取得较好的检测效果，该算法是在引入非线性函数以后，把数据空间用核函数映射到其特征空间，使其在特征空间变得线性可分，最终对降维后的数据样本集进行离群点检测。由于算法加入了降维的概念，所以能够更容易地发现样本数据集中的离群点。

实验结果与样本数据点的个数和核函数的选取有很大关系，选取不同数目的样本数据点和不同核函数所得的不同投影函数对边缘点的影响都会比较大；由于离群点通常远离任何一个类中心，从而可选用高斯径向核函数，提高第一主成分的贡献率。因为测试数据选取有限，所以没能进行更广泛的测试，通过观察检测结果，发现其中有很多是分散样本数据点归为一类，而一类最多包含的样本数据又过多，可见每一类所包含样本数不太平衡，还有待改进。

《4　结语》

4　结语

离群点检测是从大量数据对象中挖掘出少数的具有独特行为模式的数据对象，从而揭示出大量数据中隐含的有价值的知识，在诸如电子商务犯罪、电信和信用卡欺诈的侦查、视频监视和网络入侵监测等领域具有广泛应用前景[8]。

大多数离群点检测算法对高维数据的检测效果都不很理想，面对庞大的高维数据集中的离群数据发现问题，提出了一种基于非线性数据变换的离群点检测算法。该算法首先用数据变换对输入数据进行预处理，数据预处理的一个重要结果就是得到降维的向量。通过对所得数据对象每个投影分量逐个判断数据点是否是离群点，然后利用离群标记对数据集进行数据分离并输出，实验表明该算法不但可用于线性可分数据集，而且可用于线性不可分数据集。并且在克服维数灾难问题上，表现该算法的优越性。