Mathematical and Predictive Models of SARS Epidemic Disease and Mechanism of Prevention and Control

Abstract

First, based on the law of disease propagation and conservation of population statistics, this paper sets up mathematical models of four kinds of person for SARS, applies mathematical method to analyze the model, and it gets the physiology senses of the mathematical model and mechanism of prevention and control respectively. Second, it sets up predictive models of SARS epidemic disease using BP artificial neural network. According to the data of SARS in Beijing, it predicts and analyzes the model. The experimental results show that the method is simpler, and more effective with high prediction precision。

Content

《1 引言》

1 引言

传染病是当今世界最严重的问题之一。2003年春天, 非典型肺炎 (SARS) 传染病突然侵袭了大半个中国, 由于人们对此种传染病的传播机理还不太清楚, 因而一度引起了人们心理上的恐慌。现在, 预防和控制SARS的研究显得极其紧迫。目前, 对传染病的研究有4种方法:描述性研究, 分析性研究, 实验性研究和理论性研究。在理论性研究中, 数学模型起着极其重要的作用。它把传染病的主要特征通过假设、参数、变量和它们之间的联系清晰地揭示出来。数学模型的分析结果能提供许多强有力的理论基础和概念。用数学模型帮助发现传染病的传播机理, 预测传染病的流行趋势已成为共识。

利用非线性动力学的方法建立传染病的数学模型, 来研究传染病是否会蔓延持续下去以及是否终将会被消灭具有重要的现实意义。因为这有助于人们对传染病的发展趋势进行预测, 为人们预防和治疗传染病提供有益的信息和有效的措施。Kermack和Mckendrick^[1,2,3] 的论文是传染病数学模型的基石, 他们首先利用非线性动力学的方法建立了传染病的数学模型, 即所谓的KM模型, 之后, Cooke^[4], Hethcote^[5] 等做了大量的工作。陈兰荪、陈健^[6] 详细阐述了传染病的建模思想和研究方法。笔者利用非线性动力学的方法建立了非典型肺炎 (SARS) 传染病四类人的数学模型, 并探索了预防和控制SARS的机理。然后, 利用人工神经网络理论建立了SARS的预测模型, 以北京市的SARS数据为例进行了预测和分析, 预测结果显示, 该模型简单易行, 预测精度高。

《2 四类人模型[7]》

2 四类人模型[7]

SARS传染病四类人数学模型如下:

把人口分为健康人S (t) 、SARS病人I (t) 、病愈免疫 (包括死亡) 的人R (t) 及SARS疑似病人P (t) 四类人。

疾病传播一般服从下列法则:

法则1 在所考虑的时期内, 人口总数保持在固定水平N;

法则2 易受传染者S (t) 人数的变化率正比于传染病患者I (t) 与S (t) 人数的乘积;

法则3 由I (t) 向R (t) 转变的速率与I (t) 成正比。

由上述疾病传播法则, 不难得出SARS传染病四类人的数学模型为

${\begin{cases} d S / d t = - λ Ι S \\ d Ι / d t = λ Ι S - α Ι \\ d R / d t = α Ι \\ d Ρ / d t = β Ι \end{cases} (1)$ ${\begin{cases} d S / d t = - λ Ι S \\ d Ι / d t = λ Ι S - α Ι \\ d R / d t = α Ι \\ d Ρ / d t = β Ι \end{cases} (1)$

方程组式 (1) 是四维的。且初始状态为S (0) = S₀>0, I (0) = I₀>0, R (0) =R₀ > 0, P (0) =P₀ = 0。其中常数λ, α称为传染率和移除率, 其值均大于零。β>0。

令σ=αλ, 1σ=αλ称为相对移除率。为了讨论问题的方便, 假设总体N=1。

定理1 (阈值定理) 设S (t) , I (t) , R (t) , P (t) 是初值问题式 (1) 的解。如果σS₀<1, 那么, 当t→+∞时, I (t) 单调减少趋于零;如果σS₀>1, 那么, 当t→+∞时, I (t) 先增加达到最大值1-1σ-1σln (σS₀) , 此时S=1σ, 而后单调减少趋于零。S (t) 是一个单调减少函数, 并且其极限 $\lim_{t \to + \infty} S (t) = S (+ \infty)$ $\lim_{t \to + \infty} S (t) = S (+ \infty)$ , 是方程 $1 - S + (\ln ε / ε_{0}) / σ = 0$ $1 - S + (\ln ε / ε_{0}) / σ = 0$ 在 (0, 1/σ) 内的根。当t→+∞时, R (t) →0, P (t) →0 (见图1) 。

《图1》

图1S (t) , I (t) , R (t) , P (t) 的变化趋势

Fig.1 The changing trend of S (t) , I (t) , R (t) , P (t)

由于人类对传染病的认识提高以及现代医学水平的发展, 对于许多传染病可以做到提前预防, 使人群对许多种传染病具有免疫能力, 例如打预防针、进行免疫接种等。在不久的将来人类将找到SARS的免疫疫苗, 因而在模型式 (1) 的基础上考虑这些因素, 经过调整, 得到如下的数学模型:

${\begin{cases} d S / d t = - λ Ι S - δ S \\ d Ι / d t = λ Ι S - α Ι \\ d R / d t = α Ι \\ d Ρ / d t = β Ι \end{cases} (2)$ ${\begin{cases} d S / d t = - λ Ι S - δ S \\ d Ι / d t = λ Ι S - α Ι \\ d R / d t = α Ι \\ d Ρ / d t = β Ι \end{cases} (2)$

其中, δ>0。以下对模型式 (2) 进行分析, 在 (S, I) 相平面上考察轨线。首先由

$d S / d t = - λ Ι S - δ S = - (λ Ι S + δ S) < 0,$ $d S / d t = - λ Ι S - δ S = - (λ Ι S + δ S) < 0,$

得到的S (t) 是单调减少的, 所以, 对于所有t>0, 有S (t) <S₀, 再由方程dI/dt =λIS-αI =λI (S-1/σ) 可知, 当S₀≤1/σ 时, 有dI/dt<0, 对所有t>0成立, 此时I (t) 单调减少。当S₀>1/σ时由S (t) 单调减少可得到唯一的t₁, 使S (t₁) = 1/σ, 因此有0<t<t₁时, dI/dt>0, 此时I (t) 增加, t>t₁后dI/dt<0, 此时I (t) 单调减少, 所以I (t₁) 是最大值。即在相平面上的轨线I (r) 在r =1/σ时, I (1/σ) 为最大值。

显然方程组式 (2) 的轨线方程为

$Ι (t) + \ln | \frac{Ι (t)}{Ι (0)} | = 1 - S + \frac{1}{σ} \ln (\frac{S}{S_{0}}) 。$ $Ι (t) + \ln | \frac{Ι (t)}{Ι (0)} | = 1 - S + \frac{1}{σ} \ln (\frac{S}{S_{0}}) 。$

由此得

$\begin{array}{l} Ι (\frac{1}{σ}) = 1 - \frac{1}{σ} - \frac{1}{σ} \ln (σ S_{0}) - \ln | \frac{Ι (1 / σ)}{Ι_{0}} | < \\ 1 - \frac{1}{σ} - \frac{1}{σ} \ln (S_{0} σ) 。 \end{array}$ $\begin{array}{l} Ι (\frac{1}{σ}) = 1 - \frac{1}{σ} - \frac{1}{σ} \ln (σ S_{0}) - \ln | \frac{Ι (1 / σ)}{Ι_{0}} | < \\ 1 - \frac{1}{σ} - \frac{1}{σ} \ln (S_{0} σ) 。 \end{array}$

上式说明采取预防措施后, 可以减少得病人数, 并且I (t) 的最大值小于不采取预防措施时的最大值。

令 D={ (S, I) 0≤S≤1, 0<I (t) ≤1, S+I= 1}是一个由S轴到I轴以及直线S+I =1所围成的三角形区域。

对于方程组式 (2) , 其轨线为:

$\begin{array}{l} S = 0, Ι = Ι_{0} e^{- α t}, \\ Ι = 0, S = S_{0} e^{- δ t} 。 \end{array}$ $\begin{array}{l} S = 0, Ι = Ι_{0} e^{- α t}, \\ Ι = 0, S = S_{0} e^{- δ t} 。 \end{array}$

O (0, 0, 0, 0) 点是式 (2) 在D上唯一的平衡点, 并且点 (0, 0, 0, 0) 是局部渐近稳定的, 这是因为特征根-δ及-α 均小于零。

对于直线S+I=1上的所有解均有

$d (S + Ι) / d t = - α Ι - δ S < 0 。$ $d (S + Ι) / d t = - α Ι - δ S < 0 。$

所以, 在D内出发的轨线不会越出区域D。

令 $\bar{D} = {(S, Ι)$ $\bar{D} = {(S, Ι)$ 0≤S≤1, 0<I (t) ≤1, S+I = 1}在 $\bar{D}$ $\bar{D}$ 上取Dulac函数B (S, I) =1I (t) , 由Dulac定理^[8,9,10]知在 $\bar{D}$ $\bar{D}$ 上不存在极限环, 所以由 $\bar{D}$ $\bar{D}$ 上出发的轨线当t→+∞时, 必趋于平衡点 (0, 0, 0, 0) 。

综上所述, 得出如下定理:

定理2 对于初值问题式 (2) , 区域 $\bar{D}$ $\bar{D}$ 是平衡点O (0, 0, 0, 0) 的渐近稳定区域 (见图1) 。

定理3 (阈值定理) 设S (t) , I (t) , R (t) , P (t) 是初值问题式 (2) 的解。如果σS₀ <1, 那么, 当t→+∞时, I (t) 单调减少趋于零;如果σS₀ >1, 那么, 当t→+∞时, I (t) 先增加到达最大值I (1σ ) , 而后单调减少趋于零。S (t) 同时单调减少趋于零。当t→+∞时, R (t) →0, P (t) →0

通过建立四类人的SARS传染病数学模型并对其进行分析的基础上, 可得到如下结论:

1) 在不考虑自然出生和死亡的前提下, SARS传染病发生时, 如果易感染人的总数小于等于该病的相对移除率, SARS不可能发生流行, 将很快被消灭。如果易感染人的总数大于该病的相对移除率, SARS可能发生流行, 得病的人数将猛增, 当易感染人数下降到S= (1σ) 时, 得病人数I (t) 达到最大值1-1σ- (1σ) ln (σS₀) , 而后得病人数逐渐减少, 最终趋向于零, 即SARS被消灭。在整个过程中易感染人数单调减少, 最终并不是所有的易感染人都会得病。因此, 疾病不是因为缺少受传染者而停止传播, 而是因为没有了传染者才停止传播。

2) 在SARS传染病流行之前, 对易感染的人群进行有效的预防可以使易感染的人数下降, 从而达到防止SARS传染病流行的目的。在SARS传染病发生之后, 立即对易感染的人群进行隔离, 同样可以使易感染的人数下降, 从而减少得病人数。此种情况下, 如果在发病初期易感染的人数S₀≤ (1σ) , 那么SARS会很快被消灭。如果在发病初期易感染人数S₀> (1σ ) , 那么得病人数先增加, 当其达到最大值I (1σ) 后, 得病人数逐渐减少而后SARS被消灭。此种情况下的最大值I (1σ) 小于不预防时的最大值1-1σ- (1σ) ln (σS₀) 。

《3 利用人工神经网络理论建立SARS预测模型[11]》

3 利用人工神经网络理论建立SARS预测模型[11]

目前, 用于预测的定量化方法尽管很多 , 但基本上可归纳为时间关系、结构关系和因果关系模型等三类^[11]。时间关系模型的特点为被预测对象是时间变量的函数 , 它包括两种:一是数理统计学中的时间序列分析模型, 二是用时间函数 (如多项式 , 正余弦等 ) 表示的趋势外推模型。结构关系模型的特点是在一定时间内被预测事件与其影响因素之间保持着某种固定的结构函数关系 (如回归模型、联立方程模型、动态模型等) 。因果关系模型的特点是用因果关系表达被预测事件与其影响因素之间的相互作用。一般来说, 应用时间关系模型和结构关系模型时, 要求被预测对象必须满足预测模型的前提条件, 否则预测结果不可靠; 而因果关系模型实际上是因和果之间的映射关系, 几乎可以表达所有非线性关系 (如人工神经网络) , 因而比以上二类函数的适用范围广。人工神经网络 (ANN, artificial neural network) 理论是在综合了众多学科理论的基础上发展起来的, 其发展在预测方面为各领域的应用带来了广阔前景, 特别是地质、天文、机械等理工科领域。近年来, 人们才逐渐将 ANN技术用于生物、医学、药学、化学等学科, 但主要是应用 ANN进行分类或进行静态分析, 例如用蛋白质一级结构预测二级结构、药物筛选、恶性肿瘤的生存分析、疾病的诊断及预后分析等^[11]。笔者拟用误差反向传播 (BP, back-propagation) 神经网络对北京市SARS的发病率进行分析, 建立 SARS发病率的 ANN预测模型, 旨在探讨 ANN预测模型在疾病发病率或死亡率预测上的应用前景。

《3.1 三层 BP神经网络的结构》

3.1 三层 BP神经网络的结构

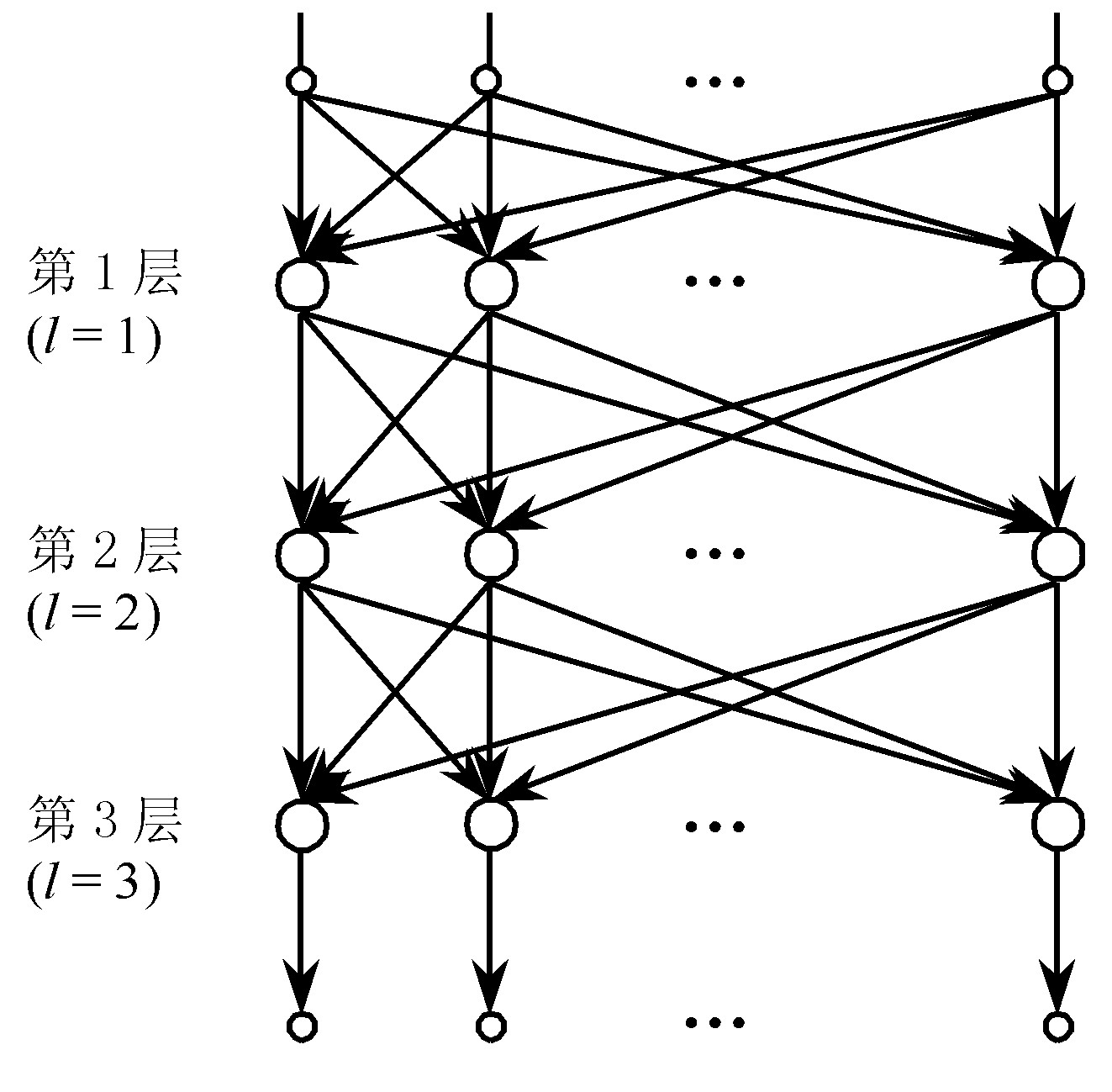
BP神经网络模型是人工神经网络中应用最广泛的一种。它的功能函数为S型函数, 神经元连接形式为前馈神经网络, 学习方式为有监督学习。如图 2和图3所示 , 整个学习过程的具体步骤为:

《图2》

图2 BP网络模型结构

Fig.2 Structure of BP ANN model

《图3》

图3 BP神经网络模型建立步骤

Fig.3 Steps of Setting up BP ANN Model

Step 1 初始化网络及学习参数, 如设置网络初始权矩阵、参数α等;

Step 2 提供训练模式、训练网络、直到满足学习要求;

Step 3 前向传播过程:对给定训练模式输入, 计算网络的输出模式, 并与期望模式比较, 如有误差, 则执行Step 4, 否则返回Step 2;

Step 4 向后传播过程:计算同一层单元的误差e $_{j}^{k}$ $_{j}^{k}$ ;修正权值和阈值, 返回Step 2, 直至全部m个学习模式对训练完毕。

各个连接权的调整量是分别与各个学习模式对的误差函数E_k成比例变化的, 该方法称为标准误差反向传播算法 (又称平均误差) , 网络的全局误差为

$E = \sum_{k = 1}^{m} E_{k} = \sum_{k = 1}^{m} \sum_{t = 1}^{q} (y_{t}^{k} - c_{t})^{2} / 2 (3)$ $E = \sum_{k = 1}^{m} E_{k} = \sum_{k = 1}^{m} \sum_{t = 1}^{q} (y_{t}^{k} - c_{t})^{2} / 2 (3)$

BP学习算法实质上是最小均方 (LMS) 算法的推广, 是一种非线性梯度优化算法, 因此不可避免地存在局部极小值问题。学习算法的收敛速度很慢, 通常需要上千次迭代或更多。为此, 采用了动态学习比率 BP算法。在BP算法中, 连接权值的改变规则为:

$\begin{array}{l} Δ γ_{t} = α \cdot d_{t}^{k} t = 1, 2, \dots, q (4) \\ Δ θ_{j} = β \cdot e_{j}^{k} j = 1, 2, \dots, p (5) \end{array}$ $\begin{array}{l} Δ γ_{t} = α \cdot d_{t}^{k} t = 1, 2, \dots, q (4) \\ Δ θ_{j} = β \cdot e_{j}^{k} j = 1, 2, \dots, p (5) \end{array}$

其中, α, β 为定义的权值步长, 即学习比率, 以下均用η表示。若η选择的很小, 网络的学习速度不但很慢, 而且很容易使网络陷入局部最小点;而η选择的太大 , 又容易使网络出现振荡, 使误差E始终不能达到极小点。因此, 对 BP网络的学习算法做以下改进:

赋予η相对较大的初始值, 使网络在学习初期误差较大, 以较大的步长逼近极值点, 同时又容易跳开局部极小点。随着网络的学习 , 根据学习误差的变化改变学习因子η, 设n为学习次数, 有

$n = {\begin{cases} (1 - 0.05) η E_{n + 1} \leq E_{n} \\ (1 + 0.05) η E_{n + 1} > E_{n} \end{cases} (6)$ $n = {\begin{cases} (1 - 0.05) η E_{n + 1} \leq E_{n} \\ (1 + 0.05) η E_{n + 1} > E_{n} \end{cases} (6)$

BP人工神经网络模型结构和建立步骤见图2和图3。

《3.2 基于 BP网络的非线性时间序列预测原理》

3.2 基于 BP网络的非线性时间序列预测原理

已知时间序列{X_ii=1, 2, …, t-1} , 若用过去的N (N≥1) 个时刻的数值预测未来M (M≥1) 个时刻的数值时, 可将训练数据分为 K段 , 长度为N+M的有一定重叠的数据段, 每一段的前N个数据作为网络的输入, 后M个数据作为网络的输出 (见表1) 。

表1 训练数据的分段方法

Table 1 The method of dividing section for training data

《表1》

N个输入	M个输出
X₁, X₂, …, X_N	X_N+1, X_N+2, …, X_N+M
X₂, X₃, …, X_N+1	X_N+2, X_N+3, …, X_N+M+1
X₃, X₄, …, X_N+2	X_N+3, X_N+4, …, X_N+M+2
	
X_K, X_K+1, …, X_N+K-1	X_N+K, X_N+K+1, …, X_N+K+N-1

然后应用前述的BP神经网络进行训练学习, 寻找一个R^N到R^M的函数关系。该网络的输入层有N (N≥1) 个节点, 输出层有M (M≥1) 个节点。

其预测值的一般形式为:

$\begin{array}{l} X_{t} = f_{1} (X) X_{t - 1} + f_{2} (X) X_{t - 2} + \dots + \\ f_{p} (X) X_{t - p} + ε_{t} (7) \end{array}$ $\begin{array}{l} X_{t} = f_{1} (X) X_{t - 1} + f_{2} (X) X_{t - 2} + \dots + \\ f_{p} (X) X_{t - p} + ε_{t} (7) \end{array}$

其中p为预测网络的输入节点数。

f_i (X) =f_i (X_t-1, X_t-2, …, X_t-p, ε_t) , (i=1, 2, …, p) 是一个以预测网络各输入变量为自变量的非线性函数。预测误差为

$σ^{2} = \sum (\hat{X}_{t} - X_{t})^{2} (8)$ $σ^{2} = \sum (\hat{X}_{t} - X_{t})^{2} (8)$

神经网络的训练过程就是使σ²达到全局最小的过程 , 也是预测模型的建立过程。从统计学观点看, 神经网络建模的最终结果是求出非线性函数f_i (X) , 而f_i (X) 是用网络中各节点的连接权阈值表示的。而用传统的时间序列AR (p) 模型进行预测, 其预测值的一般形式为

$X_{t} = C_{1} X_{t - 1} + C_{2} X_{t - 2} + \dots + C_{p} X_{t - p} + ε_{t} (9)$ $X_{t} = C_{1} X_{t - 1} + C_{2} X_{t - 2} + \dots + C_{p} X_{t - p} + ε_{t} (9)$

其中{ε_t}为白噪声, C_i为常系数。

《3.3 预测模型参数的确定》

3.3 预测模型参数的确定

利用神经网络来建立 SARS发病率预测模型时需要确定神经网络 BP训练中的模型参数。模型参数包括模型层数、隐含层节点数和功能函数。模型层数的确定尚无统一方法。通过试验对2个隐含层的 ANN与1个隐含层的 ANN进行比较, 前者易陷入局部极小, 误差在局部极小处振荡, 在同样学习次数的训练中, 二者所达到的误差相近, 因而选用3层 BP神经网络模型。节点数包括输入输出层节点数和隐含层节点数, 输入节点一般为输入变量的个数, 输出层节点为SARS每天发病数。隐含层节点数目的确定难度较大, 若隐含层节点太少, 网络可能不能训练;若网络节点数太多, 网络训练可能无穷无尽, 不易收敛。在选取隐含层节点数时, 根据最小上界 (LUB, least upper bound) 理论^[12], 经大量试验取隐含层节点数为 6。功能函数的确定:BP神经网络的功能函数要求处处可微分且收敛。目前的研究多用Sigmoid函数 f₁ (x) =1 (1+e^-x) , 极少使用双曲正切函数 f₂ (x) = (e^x-e^-x) (e^x + e^-x) 作为网络功能函数。

《3.4 预测结果》

3.4 预测结果

预测结果见表2。从预测结果可以看出, 所建立的人工神经网络模型较好地预测了SARS感染人数, 精度较高。事实上, 在3月1日到4月18日间, 由于北京市政府没有采取措施, SARS在社会上传播很快, 北京市采取各种隔离和防疫措施后, 疾病传播速度呈减缓趋势。研究表明, 防疫措施当时就会起作用, 隔离措施的效果在其后的第一、第二个周期并不明显, 而在第三个周期会显现出显著作用。由于5月1日至5日大多数单位放假, 外出人数明显减少, 人员流动性大大降低, 相当于隔离措施的进一步加强, 从而使该期间的可跟踪概率变大, 相当大的一部分传染源能够发现, 并被隔离, 这就使得5月11日至15日期间的新患病人数显著下降;5月6日上班后, 人员的社会流动性增加, 使可跟踪概率下降, 因此, 可能使5月16日至20日间的新患病人数有一定程度的反弹, 或者说下降的势头与5月11日至15日相比将会减弱。如果5月16日以后, 新发病人数没有反弹, 说明主要的感染途径已经能够掌握, 并实施了较有效的措施, 北京市的SARS疫情已得到有效控制。因此, 5月16日至20日是北京市SARS疫情的分水岭^[13]。

北京市防治SARS的经验以及数据分析结果表明, 为阻断SARS疫情在北京传播, 在新发病人数 (包括疑似患者中的确诊者) 在达到WHO接触疫区警报要求的数字之前, 需要保持防范措施力度, 并进一步加强公众防范意识^[13]。

表2 SARS感染人数实际值^[14]和预测值及相对误差

Table 2 The real and forecasting value which people infect SARS and the relative error

《表2》

日期	感染人数		相对误差/%	日期	感染人数		相对误差/%	日期	感染人数		相对误差/%	日期	感染人数		相对误差/%
日期	实际	预测	相对误差/%	日期	实际	预测	相对误差/%	日期	实际	预测	相对误差/%	日期	实际	预测	相对误差/%
4-19	105	110	4.76	5-03	105	111	5.71	5-17	15	14	-6.67	5-31	1	1	0
4-20	96	93	-3.12	5-04	62	65	4.84	5-18	14	15	7.14	6-01	1	1	0
4-21	102	98	-3.92	5-05	94	97	3.19	5-19	3	3	0	6-02	0	0	0
4-22	109	115	5.50	5-06	63	60	-4.76	5-20	7	7	0	6-03	0	0	0
4-23	113	118	4.42	5-07	89	92	3.37	5-21	0	0	0	6-04	0	0	0
4-24	117	112	-4.27	5-08	87	91	4.60	5-22	12	12	0	6-05	0	0	0
4-25	124	120	-3.23	5-09	41	39	-4.88	5-23	9	9	0	6-06	0	0	0
4-26	144	149	3.47	5-10	50	48	-4.00	5-24	25	26	4.00	6-07	0	0	0
4-27	126	123	-2.38	5-11	38	40	5.26	5-25	9	9	0	6-08	0	0	0
4-28	85	81	-4.71	5-12	39	41	5.13	5-26	5	5	0	6-09	0	0	0
4-29	148	153	3.38	5-13	43	42	-2.33	5-27	8	8	0	6-10	0	0	0
4-30	93	89	-4.30	5-14	23	24	4.35	5-28	2	2	0	6-11	0	0	0
5-01	113	117	3.54	5-15	18	17	-5.56	5-29	3	3	0	6-12	0	0	0
5-02	83	86	3.61	5-16	17	18	5.88	5-30	3	3	0	6-13	0	0	0

《4 结论》

4 结论

首先, 利用疾病传播的一般规律及人口守恒统计法则建立了四类人的SARS传染病数学模型, 然后运用数学方法对四类人的SARS传染病数学模型进行分析, 得出了其生理意义和预防、控制机理。其次, 利用人工神经网络理论建立了SARS的预测模型, 以北京市的SARS数据为例进行了预测和分析, 预测结果显示该模型简单易行, 预测精度高。

Show More