Some Theoretical Issues on Procedure Neural Networks

Abstract

In this paper, a novel artificial neuron model-procedure neuron model is proposed, in which the inputs are functions or procedures associated with ‘ time´. Based on these neurons, a model named procedure neural network, which is also a feedforward network with only one hidden layer, is constructed. The authors call this neural network as Procedure Neural Network (PNN) expanded on certain base functions. The related continuity, function approximation ability and computational capability theorems are proved.

Content

《1 引言》

1 引言

自从1943年McCulloch与Pitts提出第一个人工神经元网络MP模型^[1], 人工神经元网络的研究已走过了半个多世纪的坎坷道路。这期间人们曾提出了几十种较有影响力的神经元网络模型, 如Perceptron (感知机) ^[2], Adaline自适应线性元件^[3], Grossberg的自适应理论^[4,5], Anderson的BSB模型^[6], Fukushima的神经认知网络理论^[7], Kohonen的自组织映射网络^[8]等。特别是进入80年代, Hopfield的反馈网络模型^[9]以及多层BP网络^[10]的研究使人工神经元网络再次进入蓬勃发展阶段。之后, 各种具有实用意义的神经元网络模型不断涌现, 如Boltzmannn机^[11], RBF^[12], CMAC^[13]等。

在上述人工神经元网络模型中, 系统的输入均为与时间无关的常量, 即网络的输入是几何点式的瞬时输入。然而, 生物学研究表明^[14]:在生物神经元中突触的输出变化与输入脉冲的相对定时有关, 即依赖于持续一定时间的输入过程。在其它实际问题中, 大多数系统的输入亦往往是一个过程, 或一个依赖于时间的函数, 而几何点式的瞬时输入只能在理论上存在。过程式输入放宽了传统神经元网络模型对输入的同步瞬时限制, 使问题更为一般化。很多应用可归结为此问题, 如实时控制中, 控制的输入往往是依赖于时间的连续函数, 控制信号的输出既依赖于空间的聚合 (多输入) , 又与时间的累积效应密切相关;在变分问题中, 泛函的定义域一般可为一个与时间有关的过程区间;依赖于时间的多因素优化问题也都可以归结为具有过程输入的情形。具有过程式输入的神经元网络是人工神经元网络在时间域上的扩展, 是更一般化的人工神经元网络模型。因此, 研究过程神经元网络模型的拓扑结构, 函数逼近性质, 学习算法等具有十分普遍性的意义, 在实际中对于求解与过程有关的众多问题有着很大的应用价值。

《2 过程神经元》

2 过程神经元

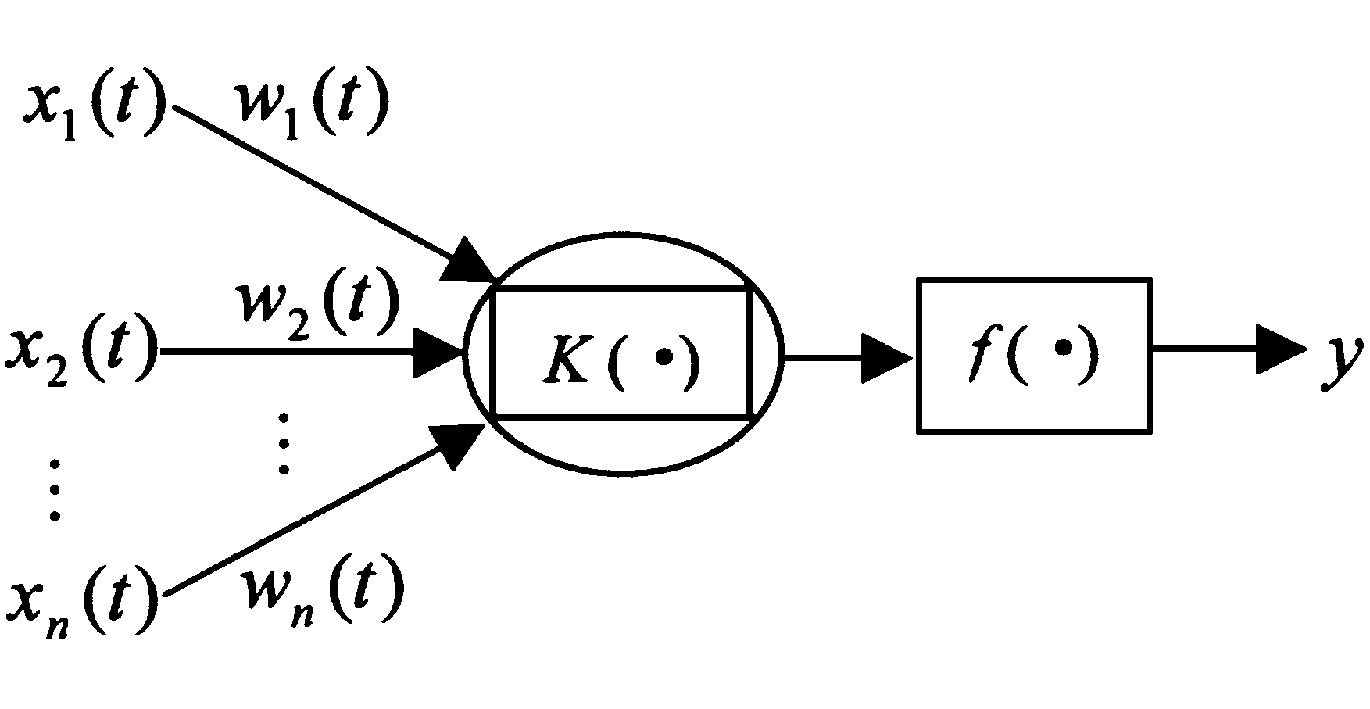
过程神经元由加权、聚合和激励三部分组成。单个过程神经元的结构图如图1所示。图1中, x₁ (t) , x₂ (t) , …, x_n (t) 为过程神经元输入函数向量;w₁ (t) , w₂ (t) , …, w_n (t) 为相应的权函数;K (t) 为过程神经元的时间聚合基函数;f (·) 为激励函数, 可取线性函数、Sigmoid函数、Gauss型函数等。

过程神经元的输入与输出之间的关系为

《图1》

图1 过程神经元

Fig.1 Procedure neuron

过程神经元的输入与输出之间的关系为

$Y = f ((W (t) \oplus X (t)) \otimes Κ (\cdot) - θ) (1)$ $Y = f ((W (t) \oplus X (t)) \otimes Κ (\cdot) - θ) (1)$

这里“⊕”表示某种空间聚合运算, “⨂”表示某种时间 (过程) 聚合运算。例如

$\begin{array}{l} W (t) \oplus X (t) = \sum_{i = 1}^{n} w_{i} (t) x_{i} (t) (2) \\ A (t) \otimes Κ (\cdot) = \int_{0}^{Τ} A (t) Κ (t) d t (3) \end{array}$ $\begin{array}{l} W (t) \oplus X (t) = \sum_{i = 1}^{n} w_{i} (t) x_{i} (t) (2) \\ A (t) \otimes Κ (\cdot) = \int_{0}^{Τ} A (t) Κ (t) d t (3) \end{array}$

其中K (·) 为[0, T]上的一个可积函数。或更一般地设K (·) 为一个一元泛函, 定义

$A (t) \otimes Κ (\cdot) = Κ (A (t)) (4)$ $A (t) \otimes Κ (\cdot) = Κ (A (t)) (4)$

一般假设权函数W (t) 和时间聚合基函数 (泛函) K (·) 均连续。由式 (1～3) 描述的过程神经元, 其内部运算由加权乘、积分、累加和以及激励函数组成, 称之为狭义过程神经元。

其实, 加权聚合运算“⊕”和“⨂”还可以取其它一般形式的运算, 例如用max和min, 或T-算子和S-算子来构成“⊕”, 激励函数f也可以是任何形式的有界函数。由式 (1, 2, 4) 描述的过程神经元被称为广义过程神经元。

《3 过程神经元网络模型》

3 过程神经元网络模型

由若干个过程神经元按一定的拓扑结构组成的网络称过程神经元网络。类似于传统神经元网络, 过程神经元网络也可以分前向型和反馈型网络。本文仅讨论前向型过程神经元网络。

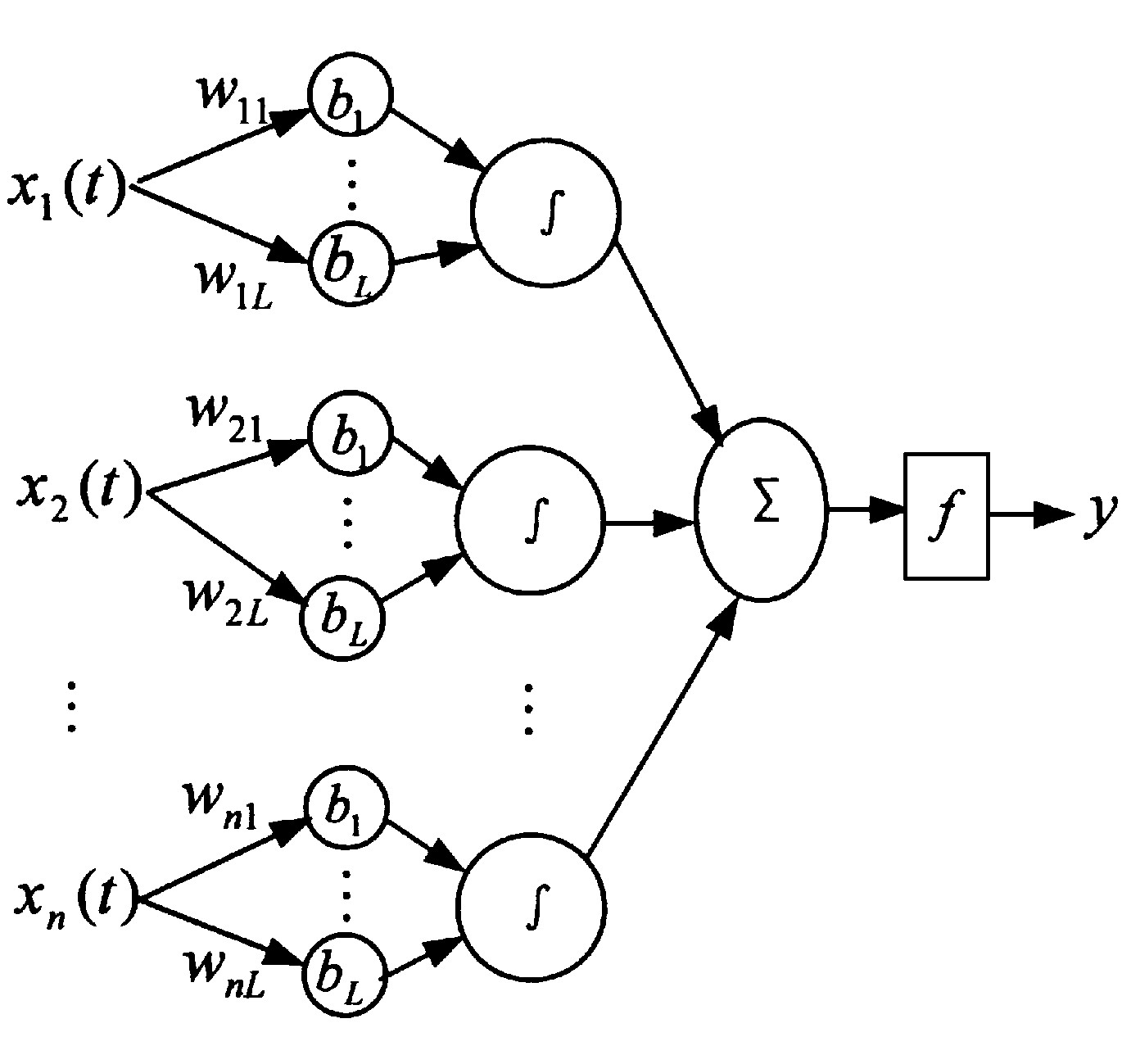
定义一种其权函数可由一组基函数展开的过程神经元网络模型。设U是泛函空间S={f (x) |x=x (t) ∈Rⁿ, t∈R, f (x) ∈V⊂R^m}上的一个紧致集, 为讨论简单起见, 取m=1, 即多输入单输出系统。也不难将结果推广到m>1的情况。假设过程神经元网络的权函数可被基函数B (t) 展开, 即将权函数的形式限制在一类较简单的函数类中来考虑问题。基函数B (t) 可以是有限基, 也可是可数基, 可以是正交的, 也可以是非正交的。这种过程神经元网络如图2所示。图2中首先把权函数按基展开, 中间各子层的运算如下:

《图2》

图2 基展开过程神经元网络

Fig.2 PNN expanded on base functions

$\begin{array}{l} w_{i} (t) = \sum_{k = 1}^{L} w_{i}^{(k)} b_{k} (t) (5) \\ A (t) = \sum_{i = 1}^{n} w_{i} (t) x_{i} (t) (6) \\ y = f (\int_{0}^{Τ} A (t) Κ (t) d t - θ) (7) \end{array}$ $\begin{array}{l} w_{i} (t) = \sum_{k = 1}^{L} w_{i}^{(k)} b_{k} (t) (5) \\ A (t) = \sum_{i = 1}^{n} w_{i} (t) x_{i} (t) (6) \\ y = f (\int_{0}^{Τ} A (t) Κ (t) d t - θ) (7) \end{array}$

或一般地有

$y = f (Κ (A (t)) - θ) (8)$ $y = f (Κ (A (t)) - θ) (8)$

其中θ为神经元的阈值, f为神经元的激励函数。函数 (泛函) K (·) 应根据实际需要来确定。

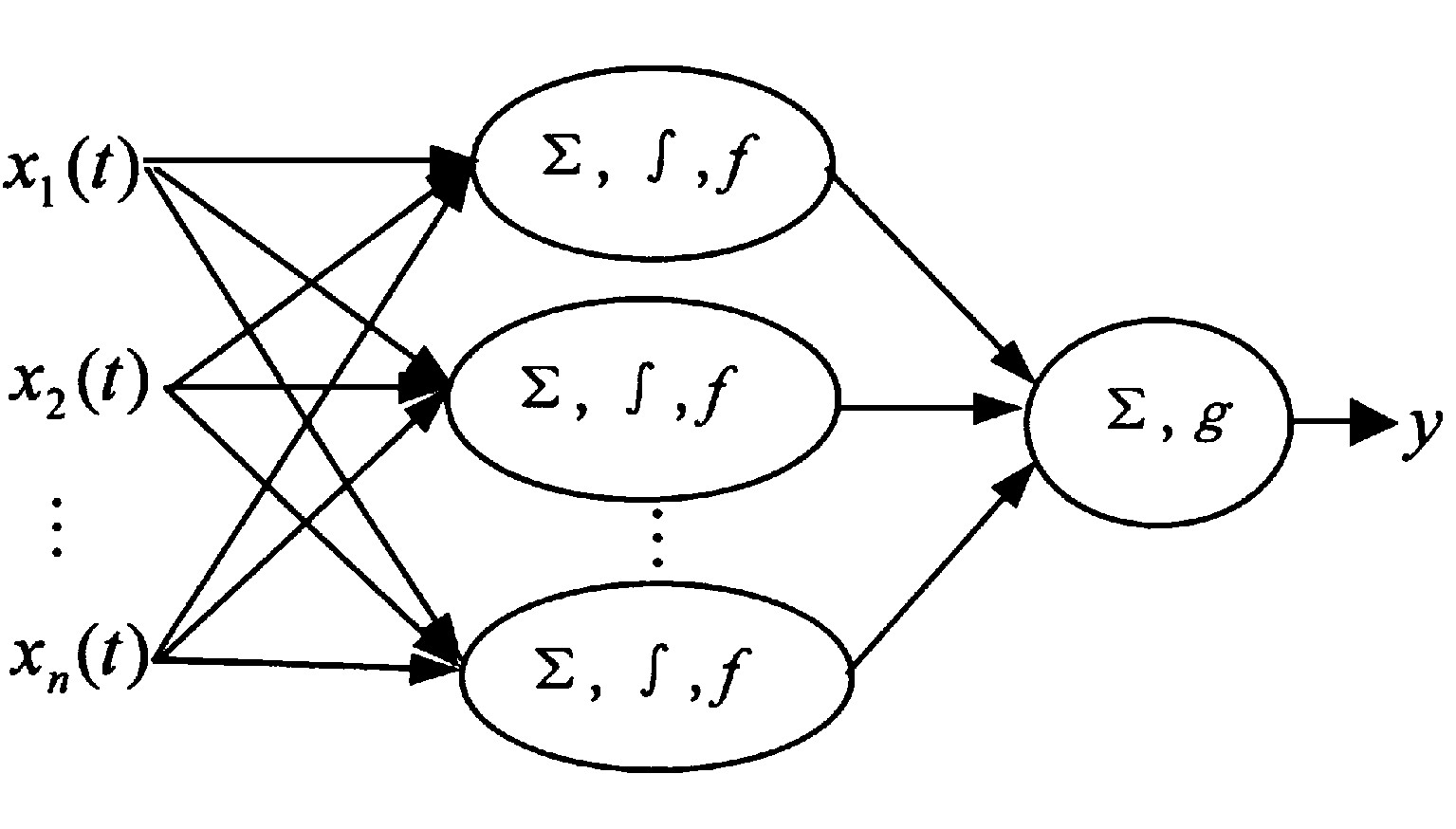
式 (7) 或式 (8) 表示的网络是一个单层过程神经元网络。下面讨论一种具有一个隐层的网络, 仍考虑多输入单输出系统, 网络的拓扑结构如图3所示。其中, 中间层 (隐层) 的各单元分别由图2中所示的神经元组成, 并设隐层有p个单元。各隐单元的激励函数和阈限可以相同, 也可以不同, 具有相同激励函数的网络称为正规过程神经元网络, 具有不同激励函数的网络称为混合过程神经元网络。输出层为一个非时变神经元。为简单起见, 仅讨论由式 (7) 定义的网络, 并设K (t) =1, 即

$\begin{array}{l} y = g (\sum_{j = 1}^{p} v_{j} f (\sum_{i = 1}^{n} \int_{0}^{Τ} (\sum_{k = 1}^{L} w_{i j}^{(k)} \cdot \\ b_{k} (t) x_{i} (t)) d t - θ_{j}) - τ) (9) \end{array}$ $\begin{array}{l} y = g (\sum_{j = 1}^{p} v_{j} f (\sum_{i = 1}^{n} \int_{0}^{Τ} (\sum_{k = 1}^{L} w_{i j}^{(k)} \cdot \\ b_{k} (t) x_{i} (t)) d t - θ_{j}) - τ) (9) \end{array}$

若假设输出层中g (u) =u, τ=0, 并令

$\begin{array}{l} w_{i j} (t) = \sum_{k = 1}^{L} w_{i j}^{(k)} b_{k} (t) (10) \\ c_{j} (x (t)) = \int_{0}^{Τ} \sum_{i = 1}^{n} w_{i j} (t) x_{i} (t) d t - θ_{j} (11) \end{array}$ $\begin{array}{l} w_{i j} (t) = \sum_{k = 1}^{L} w_{i j}^{(k)} b_{k} (t) (10) \\ c_{j} (x (t)) = \int_{0}^{Τ} \sum_{i = 1}^{n} w_{i j} (t) x_{i} (t) d t - θ_{j} (11) \end{array}$

则

$y = \sum_{j = 1}^{p} v_{j} f (c_{j} (x (t))) (12)$ $y = \sum_{j = 1}^{p} v_{j} f (c_{j} (x (t))) (12)$

《图3》

图3 含一个隐层的基展开过程神经元网络

Fig.3 PNN expanded on base functions with one hidden layer

《4 基本定理》

4 基本定理

一个合理的神经元网络模型必须具备一些最基本的特性, 包括连续性、逼近能力和计算能力等。本节就来讨论这些问题。

定理1 (连续性定理) 设式 (12) 的输入为x (t) , x^* (t) ∈U , 相应的输出分别为y, y^*∈V。若f连续, 则对任意的ε>0, 必存在δ>0, 当‖x (t) - x^* (t) ‖<δ时, 有|y- y^*|<ε。

证明:因f连续, 对任意的ε₁>0, 存在δ₁>0, 当|c_j-c^*_j|=∫ $_{0}^{Τ}$ $_{0}^{Τ}$ $\sum_{i = 1}^{n} w_{i j} (t) \cdot (x_{i} (t) - x_{i}^{*} (t)$ $\sum_{i = 1}^{n} w_{i j} (t) \cdot (x_{i} (t) - x_{i}^{*} (t)$ dt≤nTWδ₂<δ₁时, 有| (f (c_j) -f (c_j′) |<ε₁, 其中W=sup_tij|w_ij (t) |, 且‖x (t) -x^* (t) ‖<δ₂<δ₁/ (nTW) 。若记h_j=f (c_j) , h^*_j=f (c^*_j) , 对任意的ε>0, 存在δ>0, 当|h_j-h^*_j|<δ时, $| \sum_{j = 1}^{p} v_{j} h_{i} - \sum_{j = 1}^{p} v_{j} h_{j}^{*} | = | \sum_{j = 1}^{p} v_{j} (h_{i} - h_{j}^{*}) | \leq \sum_{p = 1}^{p} | v_{j} | | h_{i} - h_{j}^{*} | < p V ε_{1} < ε$ $| \sum_{j = 1}^{p} v_{j} h_{i} - \sum_{j = 1}^{p} v_{j} h_{j}^{*} | = | \sum_{j = 1}^{p} v_{j} (h_{i} - h_{j}^{*}) | \leq \sum_{p = 1}^{p} | v_{j} | | h_{i} - h_{j}^{*} | < p V ε_{1} < ε$ , 其中V=max_i{|v_i|}。只需取ε₁=ε/ (pV) , 则定理成立。

定理2 传统前馈神经元网络是过程神经元网络的一种特例。

证明: 只需在式 (9) 中取x_i (t) =x_i, b_i (t) =1, T=1, 则

$y = g (\sum_{j = 1}^{p} v_{j} f (\sum_{i = 1}^{n} w_{i} x_{i} - θ_{j}) - τ) (13)$ $y = g (\sum_{j = 1}^{p} v_{j} f (\sum_{i = 1}^{n} w_{i} x_{i} - θ_{j}) - τ) (13)$

即成为一个非时变的传统单隐层前馈神经元网络。

定义1 设K (·) :Rⁿ→V⊂R为Rⁿ到R上的任意连续函数, 记为K∈C (Rⁿ) , 定义泛函类

$\begin{array}{l} \sum^{n} (Κ) = {f : U \to V | f (x (t)) = \int_{0}^{Τ} Κ (x (t)) d t ‚ \\ x (t) \in U \subset R^{n}, f (x) \in V \subset R} \end{array}$ $\begin{array}{l} \sum^{n} (Κ) = {f : U \to V | f (x (t)) = \int_{0}^{Τ} Κ (x (t)) d t ‚ \\ x (t) \in U \subset R^{n}, f (x) \in V \subset R} \end{array}$

传统神经元网络的研究已经证明了下列熟知的逼近定理。

引理1^[10] 对任意的连续函数g (·) ∈C (Rⁿ) , 存在仅含一个隐层的前馈神经元网络可以以任意的精度逼近g。

定理3 (逼近定理) 对任意的由定义1定义的连续泛函G (x (t) ) ∈∑ⁿ (K) 和ε>0, 若满足Lipschitz条件, 则存在过程神经元网络P, 使得 ‖G (x (t) ) -P (x (t) ) ‖<ε。

证明:任取G∈∑ⁿ (K) 和ε>0, 即

$G (x (t)) = \int_{0}^{Τ} Κ (x (t)) d t (14)$ $G (x (t)) = \int_{0}^{Τ} Κ (x (t)) d t (14)$

不失一般性, 设T=1, 将K看成关于t的复合函数, 并将积分区间N等分, $t_{i} = \frac{1}{i}$ $t_{i} = \frac{1}{i}$ 为等分点, 则

$G (x (t)) = \sum_{i = 1}^{Ν} \int_{\frac{i - 1}{Ν}}^{\frac{i}{Ν}} Κ (x (t)) d t (15)$ $G (x (t)) = \sum_{i = 1}^{Ν} \int_{\frac{i - 1}{Ν}}^{\frac{i}{Ν}} Κ (x (t)) d t (15)$

设计泛函 $\tilde{G} (x (t)) = \frac{1}{Ν} \sum_{i = 1}^{Ν} Κ (x (t_{i}))$ $\tilde{G} (x (t)) = \frac{1}{Ν} \sum_{i = 1}^{Ν} Κ (x (t_{i}))$ 作为G (x (t) ) 的近似, 则

$\begin{array}{l} | G (x (t)) - \tilde{G} (x (t)) | \leq \\ \sum_{i = 1}^{Ν} | \int_{\frac{i - 1}{Ν}}^{\frac{i}{Ν}} Κ (x (t)) d t - \frac{1}{Ν} Κ (x (t_{i})) | (16) \end{array}$ $\begin{array}{l} | G (x (t)) - \tilde{G} (x (t)) | \leq \\ \sum_{i = 1}^{Ν} | \int_{\frac{i - 1}{Ν}}^{\frac{i}{Ν}} Κ (x (t)) d t - \frac{1}{Ν} Κ (x (t_{i})) | (16) \end{array}$

由于K (x (t) ) 对于t连续, 由积分中值定理, 存在 $ξ_{i} \in [\frac{i - 1}{Ν} ‚ \frac{i}{Ν}]$ $ξ_{i} \in [\frac{i - 1}{Ν} ‚ \frac{i}{Ν}]$ , 使

$\int_{\frac{i - 1}{Ν}}^{\frac{i}{Ν}} Κ (x (t)) d t = \frac{1}{Ν} Κ (x (ξ_{i})) (17)$ $\int_{\frac{i - 1}{Ν}}^{\frac{i}{Ν}} Κ (x (t)) d t = \frac{1}{Ν} Κ (x (ξ_{i})) (17)$

于是

$\begin{array}{l} | G (x (t)) - \tilde{G} (x (t)) | \leq \frac{1}{Ν} \sum_{i = 1}^{Ν} L_{Κ} ∥ x (t_{i}) - \\ x (ξ_{i}) ∥ \leq \frac{1}{Ν} \sum_{i = 1}^{Ν} L_{Κ} L_{x} | t_{i} - ξ_{i} | \leq \frac{L_{Κ} L_{x}}{Ν} (18) \end{array}$ $\begin{array}{l} | G (x (t)) - \tilde{G} (x (t)) | \leq \frac{1}{Ν} \sum_{i = 1}^{Ν} L_{Κ} ∥ x (t_{i}) - \\ x (ξ_{i}) ∥ \leq \frac{1}{Ν} \sum_{i = 1}^{Ν} L_{Κ} L_{x} | t_{i} - ξ_{i} | \leq \frac{L_{Κ} L_{x}}{Ν} (18) \end{array}$

其中, L_K, L_x分别为K (x) 关于x和x (t) 关于t的Lipschitz常数。于是

$\begin{array}{l} G (x (t)) = \int_{0}^{Τ} Κ (x (t)) d x = \\ \frac{1}{Ν} \sum_{i = 0}^{Ν} Κ (x (t_{i})) + Ο (\frac{1}{Ν}) (19) \end{array}$ $\begin{array}{l} G (x (t)) = \int_{0}^{Τ} Κ (x (t)) d x = \\ \frac{1}{Ν} \sum_{i = 0}^{Ν} Κ (x (t_{i})) + Ο (\frac{1}{Ν}) (19) \end{array}$

记x⁽ⁱ⁾=x (t_i) 。由于K (x⁽ⁱ⁾) :Rⁿ→V为C (Rⁿ) 中的连续函数, 由引理1知可用一个传统神经元网络来逼近, 再由定理2, 该传统前馈神经元网络一定能够用一个过程神经元网络来替代。即

$| Κ (x^{(i)}) - Ρ_{i} (x^{(i)}) | ＜ ε_{i} (20)$ $| Κ (x^{(i)}) - Ρ_{i} (x^{(i)}) | ＜ ε_{i} (20)$

其中ε_i>0为任意小数, i=1, 2, …, N, 不妨取ε_i<ε/ (2N) 。由式 (19) 知, 存在N₀, 当N>N₀时

$| G (x (t)) - \frac{1}{Ν} \sum_{i = 0}^{Ν} Κ (x (t_{i})) | < \frac{ε}{2} (21)$ $| G (x (t)) - \frac{1}{Ν} \sum_{i = 0}^{Ν} Κ (x (t_{i})) | < \frac{ε}{2} (21)$

记

$Ρ (x (t)) = \frac{1}{Ν} \sum_{i = 0}^{Ν} Ρ_{i} (x (t_{i})) (22)$ $Ρ (x (t)) = \frac{1}{Ν} \sum_{i = 0}^{Ν} Ρ_{i} (x (t_{i})) (22)$

则

$\begin{array}{l} | G (x (t)) - Ρ (x (t)) | = \\ | G (x (t)) - \frac{1}{Ν} \sum_{i = 0}^{Ν} Ρ_{i} (x (t_{i})) | \leq \\ | G (x (t)) - \frac{1}{Ν} \sum_{i = 0}^{Ν} Κ (x (t_{i})) | + | \frac{1}{Ν} \sum_{i = 0}^{Ν} Κ (x^{(i)}) - \\ \frac{1}{Ν} \sum_{i = 0}^{Ν} Ρ_{i} (x^{(i)}) | < ε / 2 + ε / 2 = ε (23) \end{array}$ $\begin{array}{l} | G (x (t)) - Ρ (x (t)) | = \\ | G (x (t)) - \frac{1}{Ν} \sum_{i = 0}^{Ν} Ρ_{i} (x (t_{i})) | \leq \\ | G (x (t)) - \frac{1}{Ν} \sum_{i = 0}^{Ν} Κ (x (t_{i})) | + | \frac{1}{Ν} \sum_{i = 0}^{Ν} Κ (x^{(i)}) - \\ \frac{1}{Ν} \sum_{i = 0}^{Ν} Ρ_{i} (x^{(i)}) | < ε / 2 + ε / 2 = ε (23) \end{array}$

P (x (t) ) 即为所求。

引理2 存在连续泛函K (·) , 使得对任意的x (t) = (x₁ (t) , x₂ (t) , …, x_n (t) ) 和x^* (t) = (x^*₁ (t) , x^*₂ (t) , …, x^*_n (t) ) , 当x (t) ≠x^* (t) 时, 必有K (x (t) ) ≠K (x^* (t) ) 。

证明:考虑x (t) 的第i个分量x_i (t) ∈C [0, T], 可用如下多项式逼近:

$x_{i} (t) = \sum_{j = 0}^{\infty} a_{i j} t^{j} (24)$ $x_{i} (t) = \sum_{j = 0}^{\infty} a_{i j} t^{j} (24)$

其中, {a_ij∈R}, i=1, 2, …, n;j =0, 1, 2, …。不妨设

$a_{i j} = (- 1)^{d_{i j}} \cdot 10^{p_{i j}} \cdot s_{i j} (25)$ $a_{i j} = (- 1)^{d_{i j}} \cdot 10^{p_{i j}} \cdot s_{i j} (25)$

其中, d_ij∈{0, 1}, p_ij∈Ν为自然数集合, s_ij∈ (0, 1) 。令

$\begin{array}{l} p_{i j} = n_{i 0} n_{i 1} \dots n_{i Ν j}, \\ n_{i k} \in {0, 1, \dots, 9}, k = 0, 1, \dots, Ν_{j} ‚ \\ s_{i j} = s_{i j 0} s_{i j 1} \dots s_{i j k} \dots, \\ s_{i j k} \in {0, 1, \dots, 9}, k = 0, 1, \dots, \end{array}$ $\begin{array}{l} p_{i j} = n_{i 0} n_{i 1} \dots n_{i Ν j}, \\ n_{i k} \in {0, 1, \dots, 9}, k = 0, 1, \dots, Ν_{j} ‚ \\ s_{i j} = s_{i j 0} s_{i j 1} \dots s_{i j k} \dots, \\ s_{i j k} \in {0, 1, \dots, 9}, k = 0, 1, \dots, \end{array}$

将a_ij, j=1, 2, … 作如下排列:

《图4》

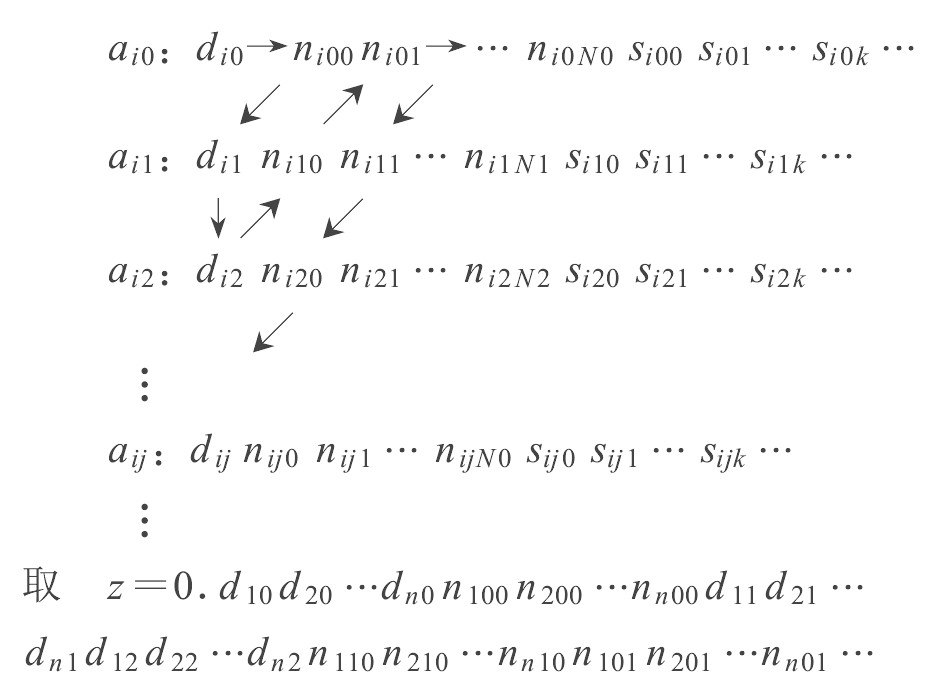
即z的小数部分排列顺序为阵列中从左上角到右下按箭头所示, 并且对于每一个位置做i的从1到n排列。显然z∈[0, 1]。将此映射关系记为K, 显然K为一一映射, 由z的取法知K (·) 连续。

定理4 (逼近定理) 对任意的连续泛函G (x (t) ) :U⊂C (Rⁿ) →V⊂R和ε>0, 存在过程神经元网络P, 使得 ‖G (x (t) ) -P (x (t) ) ‖<ε。

证明:按照引理2的构造方法, 把一个过程神经网络的逼近问题化成了一个传统神经网络的逼近问题, 根据引理1, 定理得证。

定理5 (计算能力定理) 狭义过程神经元网络的计算能力与图灵机等价。

证明:首先在狭义过程神经元网络中所用到的运算由式 (1～3) 知, 无非就是“+", “·", “∫" 以及它们的复合运算, 这些运算都可以用图灵机实现 (对“∫”运算只求近似值) , 故过程神经元网络的计算能力不会大于图灵机。另一方面, 由文献[15]知线性阈值神经元的计算能力等价于图灵机, 而线性阈值神经元又是过程神经元的特例, 因此过程神经元网络的计算能力不会小于图灵机。总之, 过程神经元网络的计算能力等价于图灵机。

《5 结论》

5 结论

本文提出了一类新的神经元网络——过程神经元网络的概念。并证明了相应的连续性定理, 逼近定理, 计算能力定理等重要理论结果。过程神经元网络是对生物神经元网络更贴切的模拟, 实际中很多应用可归结为此问题, 包括诸如某些化工和酿造等工业过程的建模和控制、农业领域内大棚栽培和室内养殖的调控和优化等。总之, 模型对于与过程有关的众多问题的解决具有广泛的应用前景。

Show More