《1 引言》

1 引言

文献[1~8]对组合证券投资问题进行了研究，构造了一些模型，并给出了相应的求解方法。文献[1]从概率角度出发，提出了一种证券投资组合模型。该模型把实现预期收益的概率作为目标函数，使之达到最大。组合贷款是指为了避免或分散大的风险，银行以多种贷款形式将资金分散贷在若干项目上。一般地，投资者的预期收益越大，他所应承担的风险也就越大。不同的银行或同一银行在不同的条件下，对获利性的要求都有所不同，但无论其预期收益如何，总是希望找到一组贷款组合，使其实现的可能性最大或者安全性最高。因此，组合贷款问题可以看成是银行的组合投资问题。

笔者提出了一种安全性第一准则下的组合贷款模型。安全性第一准则是指使贷款组合回报率低于某一水平的概率达到最小。该模型是以贷款组合回报率低于某一水平的概率作为目标函数，在满足约束的条件下，选择贷款比例，使目标函数值达到最小。在贷款收益率为正态分布的情况下，可把模型转换成确定性的等价形式，从而可以使用传统的方法求解。针对收益率不服从正态分布的情况，提出了基于随机模拟的混合优化算法求解模型。该算法集成了随机模拟技术、神经网络、遗传算法和同步扰动随机逼近算法。首先使用随机模拟技术为目标函数（不确定函数）产生一组输入/输出数据，然后使用这些数据训练神经网络用于逼近不确定函数。把神经网络嵌入到遗传算法和同步扰动随机逼近算法中。遗传算法用于在整个解空间上搜索最优解，同步扰动随机逼近算法用于改善遗传算法的初始种群和每一代由交叉和变异操作产生的新染色体。在遗传算法和同步扰动随机逼近算法中，目标函数的值通过神经网络得到。最后，给出了数值例子进行仿真。

《2 安全性第一准则下的组合贷款模型》

2 安全性第一准则下的组合贷款模型

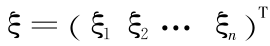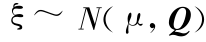选定 n 种贷款， 表示第 i 种贷款收益率，其期望值 ，i ＝ 1，2，…，n 。令 ，，其中 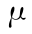 ＝（r1r2 … rn）T，Q 为随机向量 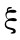的协方差阵。假定各种贷款比例为 xi，i ＝1，2，…，n，且  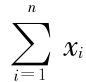＝ 1，则组合贷款的收益率为 Y 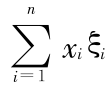＝  。令 x ＝（x1 x2  …  xn）T ，则有 Y ～ N（，）。

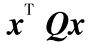假定 r 为银行所能接受的最低收益率，则在安全性第一准则下，可建立如下的组合贷款模型：

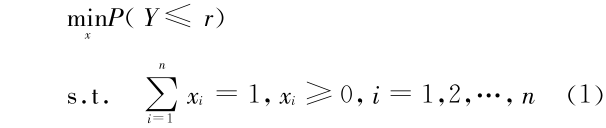
其中 P（Y r）为实际组合贷款收益率低于最低水平 r 的概率。

《3 模型的求解算法》

3 模型的求解算法

当 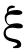服从正态分布时，可将模型（1）中的目标函数做如下变换：

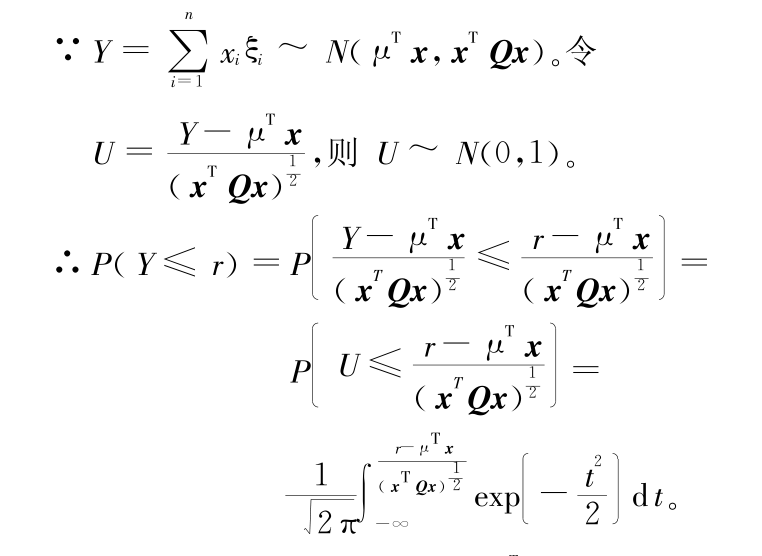
则目标函数等价变形为 。 模型（1）可表示为以下的确定性等价形式 ：

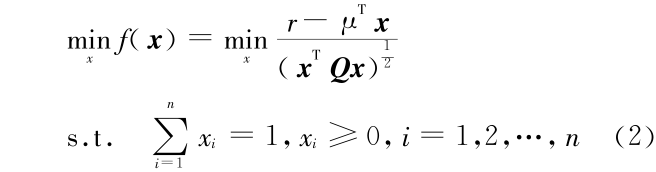
对模型（2），可以按照传统的方法来进行求解。首先对该模型做恒等变换，可得

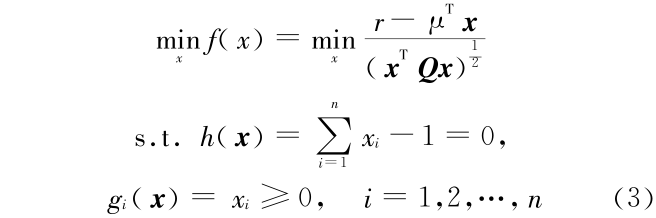
令 F =（1 1 … 1）T ∈ En，因为 h（x） = F 和 gi（x）均为单位向量，并且 gi（x） = xi（i = 1，2，…，n）不全是起作用的约束，所以起作用的约束的梯度是线性无关的。模型的最优解满足 Kuhn-Tucker 条件，即存在 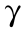和 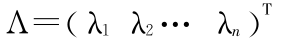使得模型（3）最优解满足下列条件：

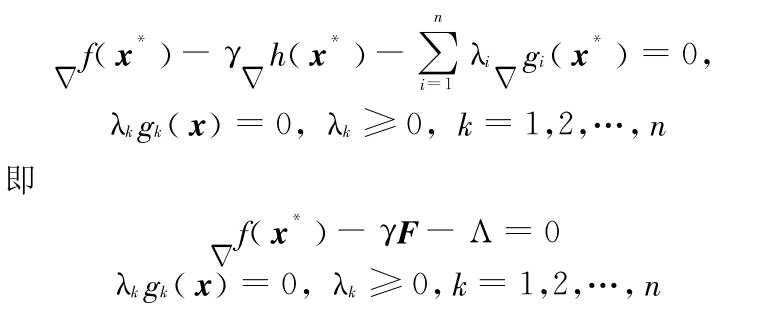
当 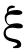不服从正态分布时，模型（1）无法转化成确定性等价形式，因此也很难用传统方法求解，但可用混合优化算法进行求解。该算法集成了随机模拟技术、神经网络、遗传算法和同步扰动随机逼近算法。

随机模拟又称 Monte Carlo 模拟，是一种实现随机（或确定）系统抽样实验的技术。虽然随机模拟是一种不很精确的技术，它提供的仅仅是一个统计估计而非一个精确值，但对那些无法用解析方法处理的随机模型，随机模拟是一种获得问题答案的有效方法。

《3.1 多维正态分布 N（，Q）随机数的产生》

3.1 多维正态分布 N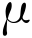（，Q）随机数的产生

步骤 1 将 Q 分解成 Q = AAT 。

步骤 2 产生 u1 u2 … un ～ N（0，1），其中 n 为多维正态分布的维数。

步骤 3 计算 z = Au + 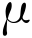，其中 u =（u1 u2 …un）T 。

步骤 4 输出 z 。

《3.2 概率 P（Y r）的随机模拟方法》

3.2 概率 P（Y r）的随机模拟方法

对于贷款收益率不服从正态分布的情况，P（Y r）不一定有相应的解析表达式，很难写出模型（1）的确定性等价类模型，计算起来也很困难。所以对于这类模型，需采用随机模拟方法来估计 P（Y r）。具体步骤如下：

步骤 1 设置迭代次数 N 。

步骤 2 对固定的 x，置计数器 N′ = 0 。

步骤 3 按照 3.1 节介绍的方法生成随机向量 z 。

步骤 4 若 Y = xTz  r，令 N′ = N′ + 1 。

步骤 5 重复步骤 3 和步骤 4 共 N 次。

步骤 6 返回 N′/N 。

《3.3 同步扰动随机逼近算法》

3.3 同步扰动随机逼近算法

在很多优化问题中，很难直接得到目标函数的值，尤其是要得到目标函数关于决策向量的梯度更加困难。但可以通过实验或模拟得到真实函数值的近似值，不能通过传统的优化方法如梯度法进行求解。 Spall 提出了同步扰动随机逼近算法，该算法基于高效且容易实现的对梯度的“同步扰动”近似，这种梯度近似在每次迭代中只使用 2 个目标函数值，而与问题的维数无关[9] 。因此，同步扰动随机逼近算法在求解大维数问题时是非常高效的。

同步扰动随机逼近算法[9] 步骤如下。

步骤 1 初始化和参数选择。令 k = 1 ，选择决策向量 x 的初始值 x1 ，然后设定参数 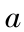，c，A ，α， 。

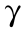步骤 2 同步扰动向量的产生。利用随机模拟产生 p 维随机扰动向量 Δk，其中第 i 个分量记作 Δki，i = 1，2，…，p 。

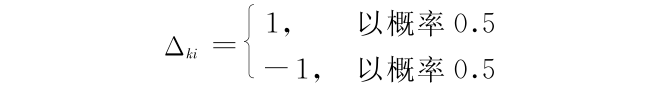
步骤 3 目标函数值的度量。计算 Ck =  c/kγ，可以通过实验或模拟得到 xk + ckΔk 和 xk - ckΔk 对应的目标函数值的近似值，分别记作 y（xk + ckΔk）和 y（xk - ckΔk）．

步骤 4 梯度近似。对未知梯度 g（xk）产生同步扰动近似：

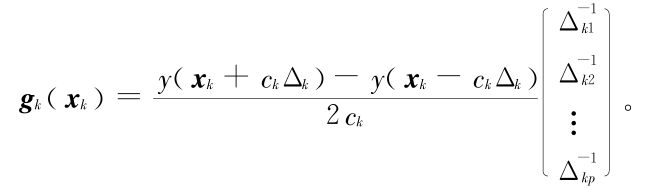
步骤 5 迭代。计算 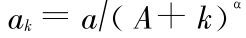，然后令 。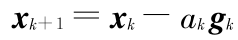

步骤 6 判断是否满足终止条件。如果满足终止条件，则转步骤 7 。否则，令 k = k + 1 ，返回步骤 2 。通常，终止准则规定为在几次连续的迭代中，函数值没有太大的变化，或达到了事先给定的迭代次数则终止。

步骤７输出结果。输出 xk + 1 和相应的目标函数值分别作为最优解和最优值。

遗传算法是一种通过模拟自然进化过程搜索最优解的方法。过去几十年中，在解决复杂的全局优化问题方面，遗传算法得到了成功的应用，并受到了人们的广泛关注。遗传算法的优点是擅长全局搜索 [10] ，但遗传算法在最优解附近的收敛速度非常慢，而同步扰动随机逼近算法具有很强的收敛特性 [9] 。混合优化算法结合了遗传算法和同步扰动随机逼近算法的优点。另外，为了减少遗传算法和同步扰动随机逼近算法过程中调用随机模拟的次数，加快优化速度，事先使用随机模拟技术为目标函数产生一组输入/输出数据，再利用这些数据训练神经网络用于逼近目标函数，把训练好的神经网络嵌入到遗传算法和同步扰动随机逼近算法中。

《3.4 基于随机模拟的混合优化算法》

3.4 基于随机模拟的混合优化算法

步骤 1 确定遗传算法中的种群规模 pop - size，交叉概率 PC ，变异概率 Pm，迭代次数 N 和同步扰动随机逼近算法中的参数 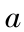，A ，c，α， 。

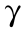步骤 2 使用随机模拟技术为如下函数产生训练用的输入/输出数据

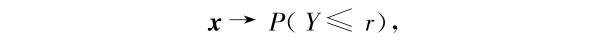
其中 x ＝（x1 x2 … xn）T 是决策向量， Y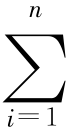＝ xi  。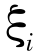

步骤 3 利用上述数据训练神经网络逼近目标函数。

步骤 4 随机产生 pop－size 个可行的染色体。

步骤 5 利用结合神经网络的同步扰动随机逼近算法来改善所有的染色体。

步骤 6 通过神经网络计算所有染色体对应的目标函数值。

步骤 7 按照目标函数值计算每一个染色体的适应度。

步骤 8 通过旋转赌轮选择染色体。

步骤 9 对依照交叉概率 PC 选择的染色体进行交叉操作。

步骤 10利用结合神经网络的同步扰动随机逼近算法来改善由交叉操作产生的新的染色体。

步骤 11 对依照变异概率 Pm 选择的染色体进行变异操作。

步骤 12 利用结合神经网络的同步扰动随机逼近算法来改善由变异操作产生的新的染色体。

步骤 13 重复步骤 6 至步骤 12 共 N 次。

步骤 14 利用结合神经网络的同步扰动随机逼近算法来改善上一步得到的所有染色体。

步骤 15 输出具有最大适应度的染色体作为最优解。

算法的流程如图 1 所示。

《图1》

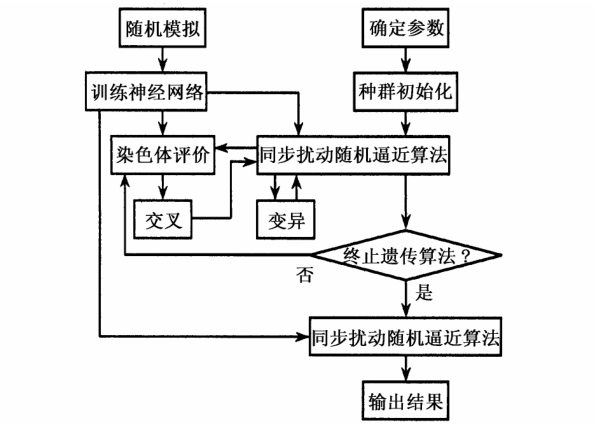
图1 基于随机模拟的混合优化算法

Fig.1 Hybrid optimization algorithm based on random simulation

《4 数值仿真》

4 数值仿真

为了验证所提出的混合优化算法求解模型的有效性，并与传统的求解方法进行比较，利用组合贷款的算例进行数值仿真

例 1 贷款的收益率服从正态分布的情况

设贷款的收益率服从正态分布 N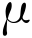（，Q），其中各种贷款的收益率为  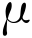= （0.12 0.09 0.10 0.09 0.09 0.11 0.11）T ，收益率协方差阵为

允许的最低收益率水平为 r = 0.1 。利用传统方法求解，得到组合贷款的最佳投资比例为 x * = （0.584 6 0.169 6 0.0 0.0 0.018 4 0.227 4 0.0）T 。模型（1）的最优目标值为 P *（Y 0.1）= 0.598 0 。

利用基于随机模拟的混合优化算法求解（在随机模拟中，取 6 000 个样本点。 Pop - size = 30，Pc = 0.3 ，Pm = 0.2 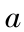， = 0.16 ，A = 100，c = 0.2 ，α = 0.602 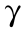， = 0.101），得到组合贷款的最佳投资比例为 x * = （0.571 2 0.011 0 0.009 3 0.015 6 0.006 1 0.383 2 0.003 6）T 。模型（1）的最优目标值为 P *（Y 0.1） = 0.422 2 。图 2 是最优目标值随迭代次数的变化情况，其中 N 表示遗传算法的迭代次数。

《图2》

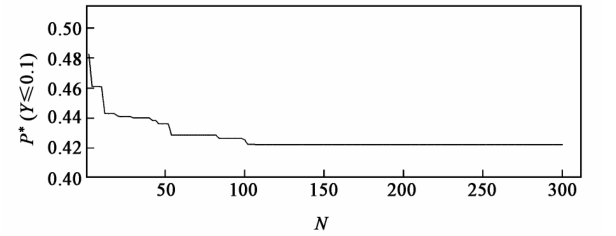
图2 例 1 中最优目标值随迭代次数的变化情况

Fig.2 Variation of optimal objective value by different numbers of iterations in Example 1

例 2 贷款的收益率不服从正态分布的情况

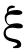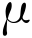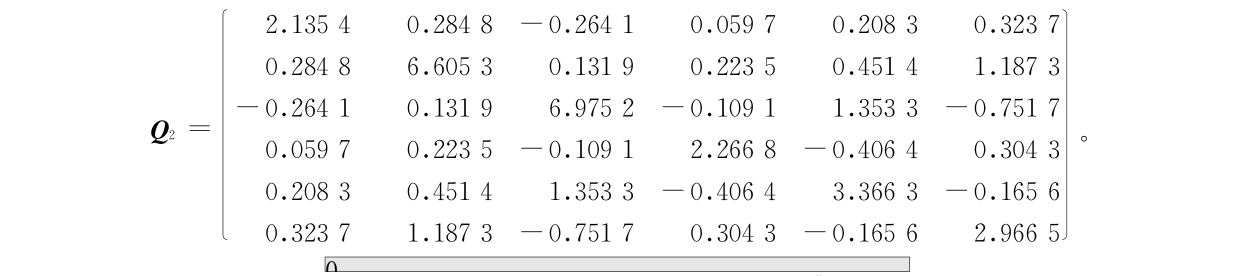
设贷款的收益率服从混合正态分布， ~ f（x），其中 f（x）＝ cf1 （x）＋（1 - c）f2（x）为混合正态分布的密度函数，f1 （x）是正态分布 N（1，Q1）的密度函数，f2（x）是正态分布 N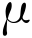（2 ，Q2 ）的密度函数，c = 0.3 ，

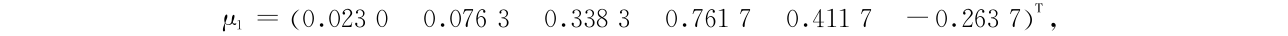
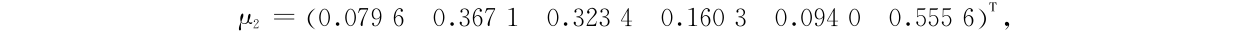
利用基于随机模拟的混合优化算法求解，组合贷款的最优投资比例为 x * = （0.000 6 0.075 7 0.161 0.370 6 0.082 4 0.309 8）T 。模型（1）的最优目标值为 P *（ Y 0.1 ) = 0.417 2 。图 3 表示最优目标值随迭代次数的变化情况，其中 N 表示遗传算法的迭代次数。

《图3》

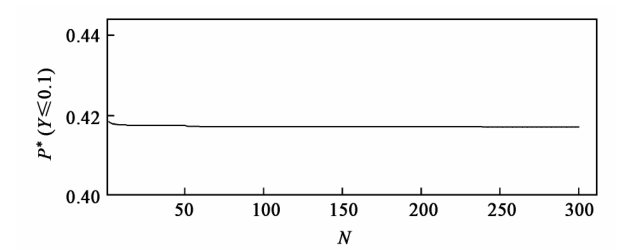
图3 例 2 中最优目标值随迭代次数的变化情况

Fig.3 Variation of optimal objective value by different numbers of iterations in Example 2

《5 结论》

5 结论

笔者提出了一种在概率准则意义下的组合贷款模型，并介绍了其传统求解方法；然后利用随机模拟、神经网络、同步扰动随机逼近算法和遗传算法相结合的思想，给出了新的求解算法。经实例仿真，验证了该算法的可行性。给出的算法突破了各种贷款收益率必须服从正态分布的假定，可对贷款收益率是任意分布形式的模型进行求解。