《1　前言》

1　前言

目前，国内外用于近岸波浪数值模拟的模型主要集中在如 Navier -Stokes 方程、缓坡方程以及Boussinesq 类水波方程等这三类。这三类方程在应用于近岸波浪的模拟中各有千秋，在研究波浪传播变形的数值模拟中，呈现出不同的特性，对于不同研究问题，每一个方程都又有不同的优缺点。作为其中的一类，Boussinesq 方程含有非线性和色散性，且将三维波浪问题简化为二维波浪问题，在其使用范围内能比较容易地给出波浪模拟，以供工程设计波浪要素等给出合理的参数值。在以往的研究中，常见方程的最佳效果，却少有研究针对一个方程的缺点进行考究。

应用于水波研究的 Boussinesq 的理论从最经典的 Boussinesq 水波方程（1967）算起[1]，到目前已有约 40 年的时间。期间国内外众多学者分别给出了不同形式的 Boussinesq 方程，使得这些方程在色散性、变浅性以及非线性等方面的性能日趋完善，这些方程的最大适用水深不断地拓展。但是方程的适用范围越大，方程的表达形式就越来越复杂，他们对应的数值模型的求解就越发困难[2~4]。为此在港口内波浪的数值计算中，简便的 Boussinesq 方程也就成为自然而然的选择。Beji 和 Nadaoka（1996）推导了简便的改进型 Boussinesq 方程[5]，很多学者对该方程进行了研究[6~7]。在该方程基础上，时间格式上采用混合四阶 Adams -Bashforth -Moulton，空间格式上采用了 Wei 等（1995）给出的格式[8]，建立了有限差分的二维数值计算模型，并通过一经典地形上波浪传播变形的实验考察了该数值模型。

《2　基本方程及数值模型》

2　基本方程及数值模型

《2.1　基本方程》

2.1　基本方程

Beji 和 Nadaoka（1996）推导的改进型的 Bouss-inesq 水波方程表达形式[5]：

式（1），（2）中， =（u，v）为二维水深平均速度； η 为波面升高； h =h（x，y）为静水面以下的水深； g 为重力加速度；为二维水平梯度算子； β=0.2 时方程的色散关系式与 Stokes 线性波色散关系的 Padé（2，2）展开式一致。

《2.2　数值模型》

2.2　数值模型

笔者在公式（1）和（2）的基础上，建立了有限差分的二维数值计算模型。

2.2.1　内部造波技术和边界处理

传统的波浪入射边界条件（波面和速度）利用造波板给出，而内部造波法的实质是在方程中引入与入射波浪要素有关的源项，该方法的优点是可以避免在初始边界采用固定造波板造波带来的二次反射问题。在内部造波技术上，典型的有 Larsen，Dancy（1983）[9]和 Wei 等（1999）[10]。在文章数值模型中，采用了 Wei 等（1999）的源项[10]，其中区别在于源项中的系数略有差异，而表达形式完全一致。

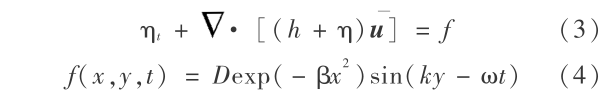
式（4）中：

此外，在开边界处采用了与 Wei 等（1999）给出的海绵边界层对波浪进行吸收[10]。在数值计算中，笔者采用了非交错网格，为了去掉由于这种网格带来的数值震荡，采用了光滑技术[11]。

2.2.2　数值模型具体表达式

式（8） ~（10）中：

2.2.3　求解过程

预报阶段：

校正阶段：

迭代阶段：无论在预报阶段还是校正阶段，波面都是直接求得，但求速度时，须用到三对角追赶法。如果校正阶段的值与预报阶段得到的值控制在设定的误差内，则该步计算结束；如不满足，则重新回到校正阶段进行计算，直到满足条件为止，笔者设置的误差为 0.000 1。

式（17）中 W 和 可代表 η，u  和 v  的校正值和预报值。

《3　数值模型的验证及分析》

3　数值模型的验证及分析

《3.1　一维波浪模拟》

3.1　一维波浪模拟

Beji 和 Battjes 及 Luth 等分别对淹没浅堤地形上的波浪传播进行了物理模型试验，对其试验结果等分别进行了潜堤上波浪传播的物理模型实验，数据来自文献[7]。模拟结果见图 1，图 1 中也给出了郑永红等利用 Crank -Nicolosn 格式计算的结果。由图 1 可以看出，笔者的计算结果与实验结果的吻合程度比郑永红等的计算结果好，这说明该格式下数值计算精度更好。但从数值结果上表明，在潜堤以后，无论是笔者提出的格式，还是郑永红等所采用的格式，均不能准确给出次峰值，这同时也说明二阶改进型 Boussinesq 方程的自身性能的不足。

《图1》

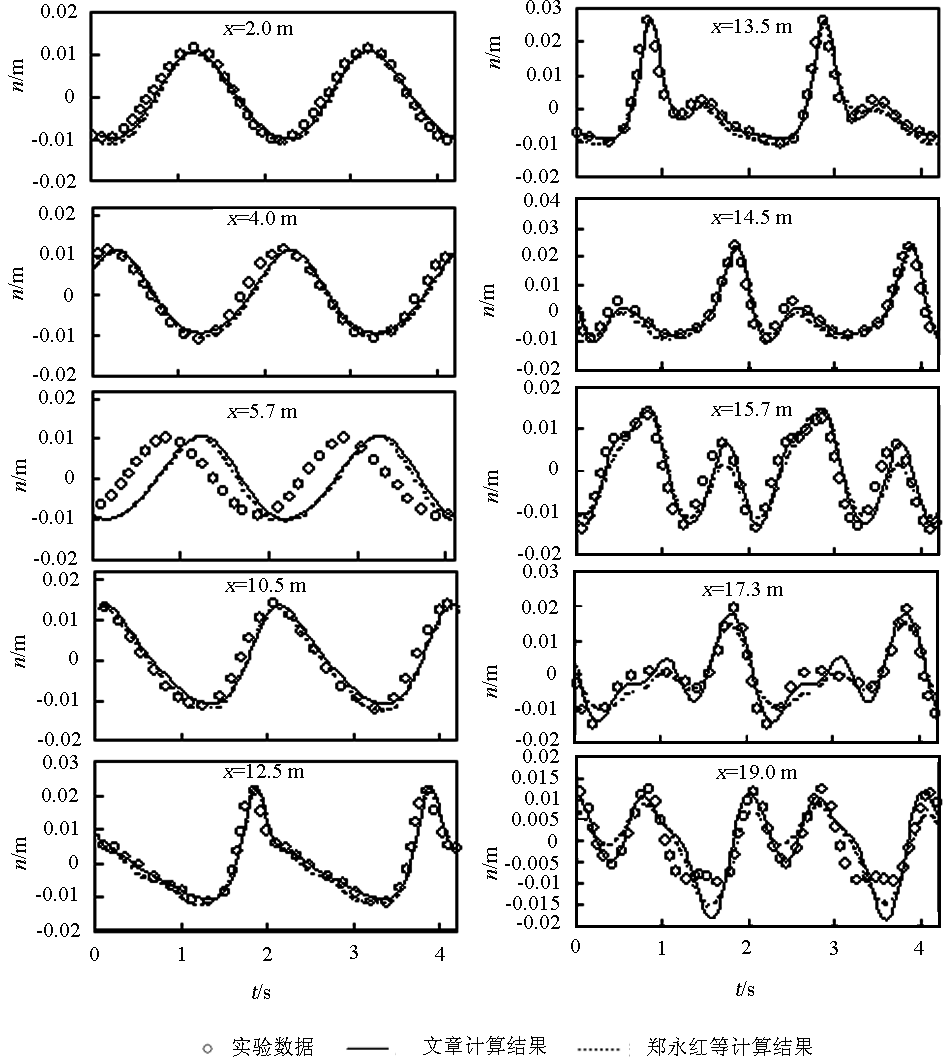
图1　不同位置处的数值模拟结果与实验数据的对比

Fig.1　Comparisons of simulated results with experimental data at different locations

《3.2 二维波浪模拟》

3.2 二维波浪模拟

Berkhoff[12]进行了椭圆形浅滩实验，后来，该实验被广泛地用来验证各类数值模型。在数值模拟中，计算区域为 30 m ×20 m，斜坡坡度为 1∶50，斜坡梯度方向与波浪入射方向的夹角为 20°。内部造波源位于 x =4 m 处的位置。斜坡旋转后的坐标与计算坐标的关系如下：

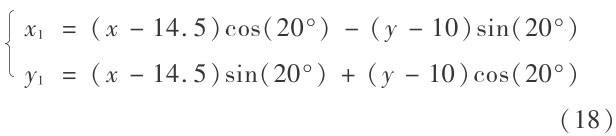
椭圆形浅滩中心坐标为（ x 1 ，y 1 ） =（0，0），浅滩边界定义如下：

平底区域及斜坡上的水深为

浅滩上水深为

波浪周期为 1.0 s，波高为 0.046 4 m，波浪正向入射。在数值模拟中，采用了空间步长为 0.1 m ×0.1 m，时间步长为 0.02 s，整个模型运行 40 s。数值计算结果与已公开发表的实验数据对比见图 2，图 2 中 H0 为入射波高，H  为计算域内的波高。波浪穿越浅滩的整个数值计算过程中，从整体效果来看，笔者的模型数值计算结果与实验结果吻合较好。图3 给出了在 t =40 s 时刻的全场波面图，图中反映出 Boussiensq 方程能综合模拟出了波浪的变浅、反射、折射和绕射等现象。

《图2》

图2　数值解与实测结果的比较

Fig.2　Comparisons of numerical results and measured wave height

《图3》

图3　t =40 s 时的全场波面图

Fig.3　Simulated surface wave at t =40 s

《4　结语》

4　结语

1）研究了一类含弱非线性的改进型 Boussinesq 方程，建立了基于非交错网格的 ABM 格式下的波浪数值模型。

2）利用数值模型对波浪的一维和二维传播问题进行了计算，结果表明对于空间点的波浪时间序列问题上，该数值模型不能准确给出潜堤后次峰，但对于沿空间的波高统计值对比上，该数值模型计算结果较为准确。

3）尽管笔者采用的是改进型 Boussinesq 方程，但以上结论中给出的问题也会出现在其他同为二阶的高阶 Boussinesq 方程的数值模拟中，这实质上也反映出二阶色散性 Boussinesq 水波方程的局限性。