《1 前言》

1 前言

学习控制是智能控制的一个高级分支，具有自动知识获取的能力。学习控制的研究热点之一是迭代学习控制，1978 年日本学者内山[1]最先提出一个控制高速运动机械手的思想，后来本卓等人[2]发展了内山的思想，于 1984 年明确了迭代学习控制（iterative learning control，ILC）的概念。ILC 经历三十多年的发展，不仅在实际应用中取得了良好效果，而且在理论上也取得了丰硕成果，其强大的生命力受到控制界的极大关注，已经成为智能控制的一个方向[3~6]。迭代学习控制在土木工程结构振动控制领域应用还很少，而工程中存在着大量的复杂振动系统，其复杂性表现为系统的非线性与模型结构的不确定性，传统的控制方法难以满足这类系统的控制需要。迭代学习控制理论为土木工程结构振动控制提供了新的方法。

迭代学习控制主要问题之一是鲁棒性问题。针对实际动态过程中各种不确定的扰动、偏差等客观存在，人们提出智能迭代学习控制算法来解决控制系统的鲁棒性问题。模糊控制是以模糊集合论、模糊语言变量和模糊逻辑推理为基础的一种计算机数字控制技术[7,8]。模糊控制不需要知道控制对象的数学模型，能克服非线性等因素的影响，且模糊控制对于变参数问题有较好的控制作用。

笔者等针对高层建筑结构的地震响应，结合自校正控制、模糊逻辑和迭代学习控制的基本思想，提出采用自整定模糊控制确定迭代学习律的方法，有效地控制高层建筑结构地震响应，提高了迭代学习控制的鲁棒性。

《2 迭代学习控制的基本原理》

2 迭代学习控制的基本原理

假定被控对象动力学模型[5]为

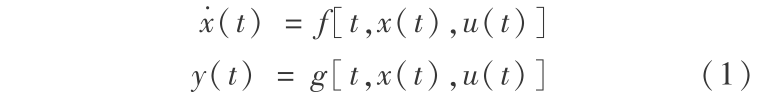
式（1）中， x ∈R n×1 、 y ∈R m×1 、u ∈R r×1 分别表示系统状态向量、输出向量及控制输入向量； f (· ) 、g (· ) 为相应维数的向量函数，其结构与参数均未知。

对于式（1）所示控制系统模型，控制任务是在时间 [ 0 , T ] 范围内，要求系统输出 y ( t ) 跟踪期望输出 yd( t ) 。

根据上述假定，第 k 次对期望轨迹跟踪时，系统模型可表示为

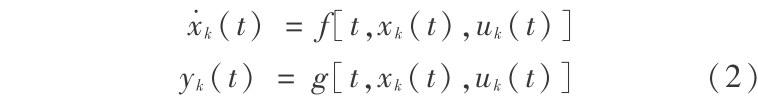
定义输出误差

如果能够恰当利用 ek( t ) 及控制输入量 uk( t )生成下一次跟踪时的控制输入

其中， φ 为学习算子。使得当 k → ∞ 时， uk( t ) → ud( t ) 、 yk( t ) → yd ( t ) ，即在 t ∈ [ 0 , T ] 范围内：

此时，在式（4）的作用下，通过对 yd ( t ) 的反复跟踪，就可以达到高精度的控制效果。

以上便是迭代学习控制的基本思想，式（4）称为迭代学习律，整个过程还可以形象地用图 1 来表示。

《图1》

图1 迭代学习控制过程原理图

Fig.1 Schematic diagram of ILC

根据以上分析，不失一般性，迭代学习控制步骤如下：a. 给定期望轨迹 yd( t ) ，选取第一次运行时的控制输入 u1( t )，t ∈ [ 0 , T ] ；b. 对被控对象施加控制输入 u1( t ) ，采样并存储输出 y1( t ) ，运行完成时计算输出误差 e1( t ) = y1( t ) - yd( t ) ；c. 利用式（4）迭代学习律计算第二次运行时的输入量 u2( t ) ；d. 重复与步骤 b 、c 相同的过程，依次得到 u3( t ) 、u4( t ) 、 u5( t ) …和相应的 e3( t ) 、 e4( t ) 、 e5( t ) …直至输出误差收敛至所期望的范围内；e. 结束。考虑高层建筑结构受控系统状态方程

式（6）中， Z = 分别代表每层的绝对位移和速度；A 、B 、C 为相应维数的系数矩阵；D 为地震波作用位置矩阵； 为输入地震波。

则任意时间 ti 的系统状态方程为

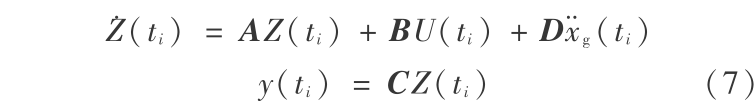
由线性二次型（LQ）经典最优控制[9]可以求得控制力为

式（8）中， PLQ (ti ) 为 Riccati 方程的解，将式（8）求得的控制力作为迭代学习初始控制力 U1 (ti ) ，相应的输出变量 y1 (ti ) 作为迭代初始状态，期望轨迹 yd ( ti ) 取零轨迹响应。

由式（7）知迭代运行 k 次的状态变量表达式为

由式（9）得到误差模型为

式（10）中，,= , =  ｡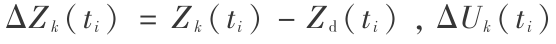

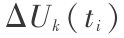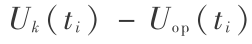由式( 9 )和式( 10 )得到状态方程

式（11）中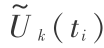，, ＝,笔者等采用自整定模糊控制器设计迭代学习律来确定每次迭代控制量的增量。

《3 自整定模糊控制器设计》

3 自整定模糊控制器设计

自整定模糊迭代学习控制是在模糊控制器的基础上，增加一个迭代学习控制环节[9~12]，笔者等提出采用模糊控制来确定迭代学习每次迭代控制量增量的方法，其原理如图 2 所示。自整定模糊控制器与传统模糊控制器的主要区别是增加了一个自调整因子 α，自调整因子的引入极大提高了模糊控制器非线性映射的平滑度，使得控制效果得以改进。

《图2》

图2 自整定模糊迭代学习控制系统

Fig.2 Auto-tuning fuzzy ILC control system

图 2 中选择了一个二维模糊控制器，其输入变量为误差 e 和误差的变化 Δe ，误差 e 由式（3 )确定，误差的变化 Δe 为误差的求导，输出变量为迭代学习控制量增量 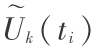，简记为 u ，其中关键是模糊控制器的设计，文章采用自整定模糊控制器，如图 3 所示。

《图3》

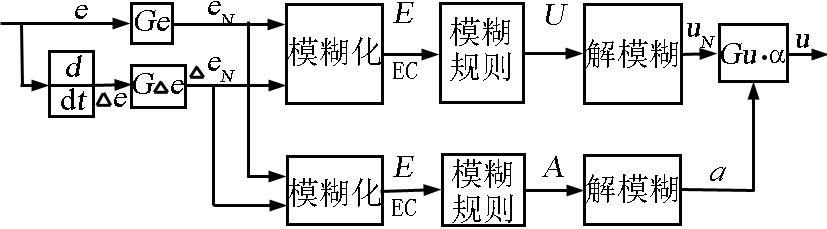
图3 自整定模糊控制器

Fig.3 Auto-tuning fuzzy controller

图 3 中 Ge 和 GΔe 分别为输入误差和误差变化的量化因子； E 和 EC 分别为误差和误差变化经过模糊化后得到的模糊变量； U 和 A 分别为输入模糊变量经过模糊推理后的输出模糊变量。Gu 为输出迭代学习控制量增量的比例因子。 以下给出自整定模糊控制器具体设计步骤：

1) 确定模糊子集及模糊论域。定义模糊变量 E 、EC 和 U 的模糊子集为｛NB，NM，NS，ZE，PS，PM，PB｝，即｛负大，负中，负小，零，正小，正中，正大｝，定义模糊变量 A 的模糊子集为｛ZE，VS，S，SB，MB，B，VB｝，即｛零，很小，小，小大，中大，大，很大｝。输入变量 e 、 Δe 和输出变量 u 的模糊子集的隶属函数被定义在归一化区间[ -1，+1 ]，变量 α 的模糊子集的隶属函数被定义在区间[ 0，+1 ]。

2) 确定隶属度函数。隶属函数是模糊集合的特征函数，是运用模糊集合论解决实际问题的基础。隶属函数的形状对系统的稳定性和快速性都有着很大的影响，一般表示隶属函数的模糊集合必须是凸模糊集合，即隶属函数的形状应呈单峰馒头形，图 4（a）为 E 、EC 和 U 模糊子集的隶属函数，（b）为自整定因子 A 模糊子集的隶属函数。 文章综合考虑论域的覆盖程度，控制系统稳定性和计算量除 NB 、PB 和 ZE 、VB 采用梯形的隶属函数外，其余模糊子集均采用简单的三角形隶属函数。

《图4》

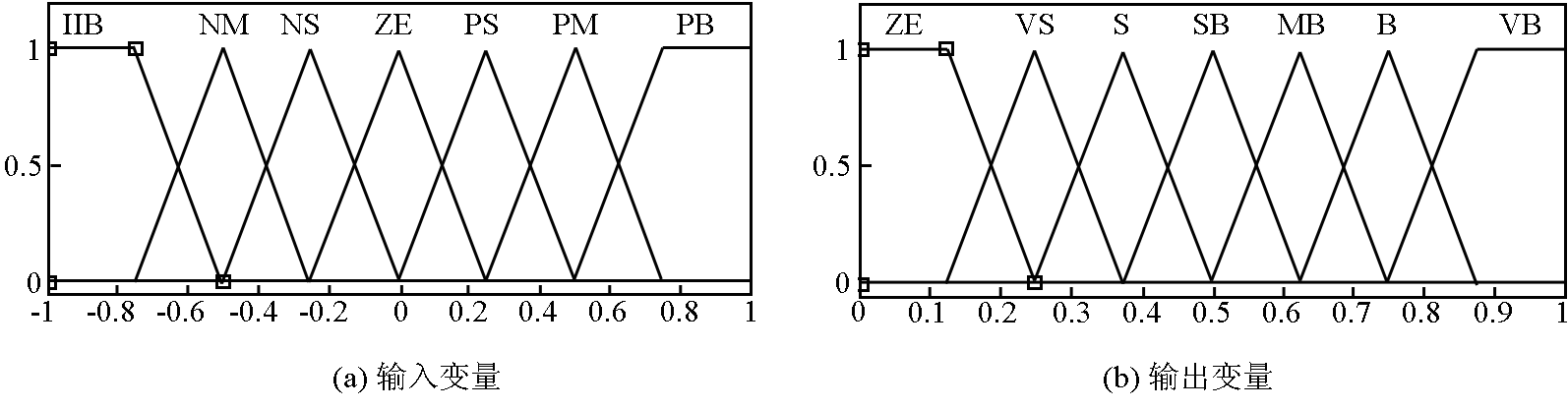
图4 模糊子集隶属度函数

Fig.4 Membership functions of fuzzy subsets

3) 量化因子和比例因子的选取。通过归一化增益，量化因子 Ge 、 GΔe 使实际输入的变量值映射到[ -1，+1 ]区间。对于传统的模糊控制器，比例因子 Gu 使控制器的输出映射到对应的实际输出值，而对于文章的自整定模糊控制器，选取的比例因子是 Gu · α 。图 3 中各变量关系如下：

式（12）中，3 个增益参数因子需要确定，不失一般性，对于第一次迭代学习，由于初始轨迹与期望轨迹均在前文确定，误差绝对值的最大值 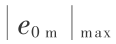可测，从而确定 Ge ， 然而误差变化绝对值的最大值 无法提前确定，需在第一次迭代学习结束后，得到所需数据后方可确定 GΔe ，输出因子 Gu 的选取需要考虑控制作用的实际可行和系统的稳定。增益因子选取如式（13）所示：

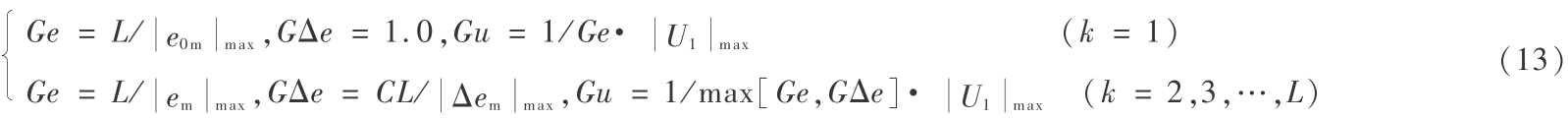
式（13）中， L 、CL 分别为误差和误差变化的讨论范围的上限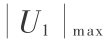； 由式（8）确定。

4) 模糊规则的确定。模糊推理规则是模糊控制器设计的关键，迭代学习控制是人对事物学习的一种形式，推理规则依据专家经验确定， uN 和自整定因子 α 的推理采用如下规则形式：if e is E and Δ e is EC then uN is U，if e is E and Δe is EC then α is A 。上述描写的模糊控制规则可采用模糊控制表来描述，推理表见表 1 、表 2 。表1 中，如果误差是“负大”（正大），并且误差变化率也是“负大”（正大），那么输出变量 U 应该是“负大”（正大），即跟踪轨迹负向（正向）远离期望轨迹，应该施加一个大的负（正）控制力增量使得跟踪轨迹朝期望轨迹运动；如果误差是“零”，并且误差变化率也是“零”，那么输出变量 U 应该是“零”，即跟踪轨迹已达到期望轨迹，不需要再施加控制力增量。表 2 中，如果误差是“负大”（正大），并且误差变化率也是“负大”（正大），那么输出变量 A 应该是“很大”，即应该给因子 α 赋予一个很大的数值，得到很大的控制力增量使得跟踪轨迹朝期望轨迹运动；如果误差是“零”，并且误差变化率也是“零”，那么输出变量 A 应该是“零”，即跟踪轨迹已达到期望轨迹，因子 α 赋值为零。模糊推理是模糊控制的核心，它利用某种模糊推理算法和模糊规则进行推理，得出最终的控制量。

《表1》

表1 uN 的推理规则表

Table1 The fuzzy reasoning rules of uN

《表2》

表2 α 的推理规则表

Table2 The fuzzy reasoning rules of α

5) 反模糊化（解模糊）。模糊控制器通过模糊推理得到的结果是一个模糊集合，它反映的是控制语言的不同取值的一种组合，但在实际模糊控制中，必须要有一个确定值才能驱动或控制执行机构，将模糊推理结果转化为精确值的映射称为反模糊化，或者称为解模糊。采用 Mamdani 型模糊控制器，模糊化关系合成运算采用取大－取小法，用相应的输入量模糊集合求输出量的模糊集合，采用面积重心法清晰化计算得到模糊集合的清晰值。

《4 数值仿真》

4 数值仿真

选取 Benchmark 模型是按美国加利福尼亚州规范（SAC )设计的 20 层抗震钢结构，模型平立面布置图参见文献[13]。SAC 设计的 20 层钢结构模型平面尺寸为 30.48 m × 36.58 m，高 80.77 m，东西方向 6 跨，南北方向 5 跨，每跨跨距均为 6.10 m，除首层层高 5.49 m 外，其余各层层高均为 3.96 m，地下两层，每层层高 3.65 m 。由于对称性，仅考虑整个结构的一半进行分析，取梁柱节点和每段柱与柱的接头作为单元的节点，共计 180 个节点 284 个单元。每个节点具有水平位移、竖向位移和平面内转角 3 个自由度。为了分析方便，结构采用剪切型模型，考虑边界约束条件和水平楼板无穷刚度假定，忽略框架各结点的竖向和转动自由度，仅仅考虑每个楼层的水平自由度。采用静力缩聚法对原有限元模型进行降阶，原结构只保留了 20 个平动自由度。其中 20 层钢结构 Benchmark 模型的楼层质量和刚度参数[14]为：m1 = 1.126 × 106 kg 、m2 ~ m19 = 1.100 × 106 kg 、m20 = 1.170 × 106 kg 、 k1 ~ k5 = 862070 kN/m 、k6 ~ k11 = 554170 kN/m 、k12 ~ k14 = 453510 kN/m 、k15 ~ k17 = 291230 kN/m 、k18 ~ k19 = 256460 kN/m 、k 20 = 171700 kN/m 。计算得到 20 层结构模型前 10 阶频率为 0.285 、0.740 、1.23 、1.663 、2.09 、2.56 、2.95 、3.42 、3.77 、4.16 Hz，结构阻尼比假定为 0.05[14]，阻尼矩阵按瑞雷阻尼确定。缩聚的模型较好地保留了原结构的动力特性。

为了说明文章所提算法的有效性，将模型在地震作用下的位移响应控制结果与全状态反馈的线性二次型调节器（linear quadratic requlator，LQR）最优控制、结构无控的结果进行比较，其中 LQR 最优控制在结构每层均安置主动控制器；最优 LQR 控制中权矩阵 ，其中 K 、M 为结构刚度和质量矩阵；I 为单位矩阵，权矩阵系数取 α = 1 、β = 1 × 10-7。利用 Matlab 编制程序，迭代学习控制期望轨迹取零轨迹响应，经典 LQR 最优控制输出响应作为初始轨迹，可得受控结构相应的系统输出误差方差值与迭代学习次数的关系曲线（见图 5 )。地震作用下的结构模型第一层位移响应在迭代学习过程中的时程曲线如图 6 至图 8 所示，从图 6 至图 8 可以看出，位移响应峰值与无控结果相比，控制效果比较明显，文章所提算法的控制结果表明模糊迭代学习控制方法能够对 Benchmark 模型的地震响应进行有效的控制。

《图5》

图5 输出误差方差值与迭代次数关系

Fig.5 Output error variance and iteration

《图6》

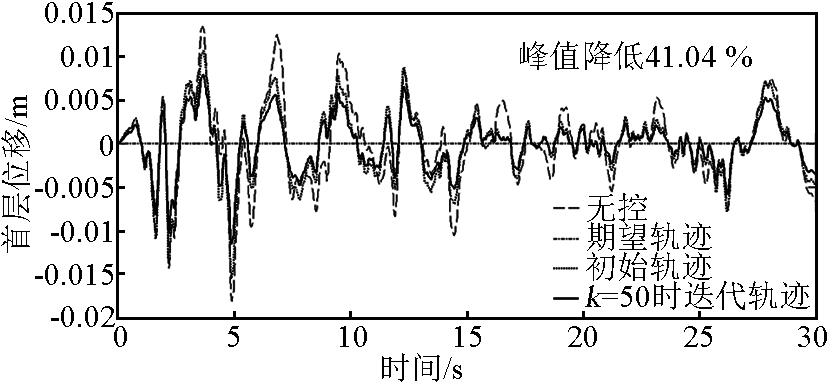
图6 结构第 50 次迭代时的位移响应

Fig.6 Displacement response on the 50th iteration

《图7》

图7 结构第 100 次迭代时的位移响应

Fig.7 Displacement response on the 100th iteration

《图8》

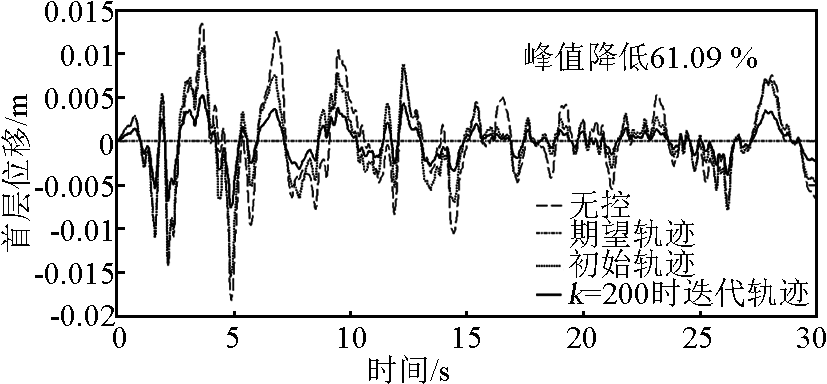
图8 结构第 200 次迭代时的位移响应

Fig.8 Displacement response on the 200th iteration

《5 结语》

5 结语

文章结合自校正控制、模糊逻辑和迭代学习控制的基本思想及各自优点，提出采用自整定模糊控制确定迭代学习律的方法，提高了迭代学习控制的鲁棒性。这种模糊控制方法适用于线性、非线性等各种被控对象，不需要被控对象的精确数学模型，对迭代学习控制过程中的模型误差、初始条件误差、量测误差和随机干扰等都具有较好的鲁棒性，需要确定的模糊控制器参数仅为三个归一化增益，操作简单实用，应用范围广。

仿真模拟结果表明该方法能够有效控制选取的 Benchmark 模型的地震响应，控制效果比较明显，说明文章模糊迭代学习控制方法应用于高层建筑结构主动振动控制领域是有效的，也验证了迭代学习控制方法在结构地震响应振动控制领域中的应用价值。