千米级斜拉桥空间非线性合理恒载索力分析

摘要

建立了斜拉桥索力调整的空间非线性有限元分析模型，以斜拉桥主梁和索塔的弯曲应变能为目标函数、结构应力及索力为约束条件，采用一阶最优化计算方法进行求解，用以确定成桥合理状态的索力。应用该法分析了某千米级斜拉桥的合理成桥状态，计算结果表明，该方法简单、有效。

正文

《1 引言》

1 引言

斜拉桥是一种高次超静定结构, 其自重引起的内力和变形可以通过调整斜拉索的张拉力而人为地进行调整。合理确定成桥索力是斜拉桥结构分析中的一项十分重要的工作。确定斜拉索索力的方法很多, 传统的有零位移法、指定应力法等。随着计算机在工程计算中的广泛应用, 采用最优化计算方法来确定斜拉桥的成桥恒载索力成为可能。由于索力具有可调性, 斜拉桥的设计自由度很大, 可以通过斜拉索力的调整来改变结构的受力分配, 优化结构的受力。因此, 一旦斜拉桥结构体系确定, 总能找出一组斜拉索力, 它使结构体系在确定性荷载作用下, 某种反映受力性能的目标达到最优, 这组索力对应的成桥态就是对应目标下的成桥合理状态^[1]。

在优化方法中, 由于优化目标的不同, 又有许多方法, 如应变能最小法、弯矩最小法、用索量最小法和最大偏差最小法等。其中最小应变能法和求解过程都是使整个结构的内力分布合理, 并以此为目标值。由于其求解出的索力能够使整个结构的恒载内力最均匀和最小, 因此具有更强的适应性及更高的实用性^[2]。但是, 当斜拉索较多时, 如果不加任何约束条件, 用该法得出的弯矩一般比较小, 但两端的索力不均匀;如人为地做索力局部调整, 容易将受力状态调乱, 难以得到索力和梁塔内力均满意的结果^[3]。文献[4]提出有约束的最小应变能法克服了上述不足。调索时既可满足对某些节点位移、截面内力或索力的特殊限制, 又可通过目标函数最小化使整个结构的弯矩及索力均匀, 从而满足不同的要求。

几何非线性是千米级斜拉桥结构体系的重要特征。由于大位移、梁柱效应以及拉索垂度等非线性因素的影响, 其目标函数及约束函数很难用拉索索力的显式形式来表达, 属于非线性优化范畴。而现有的索力优化算法如最小二乘法、影响矩阵法大多以叠加原理为基础, 只适用于线性结构。因此, 必须探索一套新的更为有效的最优化计算方法, 以用于确定桥梁的合理成桥状态。

笔者尝试将ANSYS最优化计算工具引入斜拉桥成桥合理状态的计算中, 采用一阶分析法来确定桥梁的恒载索力。建立一个以斜拉桥索塔和主梁弯曲应变能为目标函数, 由设计师任意指定的截面弯矩及索力上下限为约束条件的斜拉桥索力调整非线性分析模型, 并采用一阶最优化计算方法进行求解, 用以确定成桥合理状态的索力。在计算中, 考虑斜拉桥各种非线性因素的影响。

《2 数学模型》

2 数学模型

《2.1一阶分析法》

2.1一阶分析法

设最优化问题为

$\begin{array}{l} \min f (X) 其中 X = [x_{1} x_{2} \dots x_{n}] \\ \begin{matrix} s . t . g_{i} (X) \leq \bar{g}_{i} & (i = 1, 2, \dots ‚ m_{1}) \\ \underline{h}_{i} \leq h_{i} (X) & (i = 1, 2, \dots ‚ m_{2}) \\ \underline{w}_{i} \leq w_{i} (X) \leq \bar{w}_{i} & (i = 1, 2, \dots ‚ m_{3}) \\ \underline{x}_{i} \leq x_{i} \leq \bar{x}_{i} & (i = 1, 2, \dots ‚ n) \end{matrix} \end{array}} (1)$ $\begin{array}{l} \min f (X) 其中 X = [x_{1} x_{2} \dots x_{n}] \\ \begin{matrix} s . t . g_{i} (X) \leq \bar{g}_{i} & (i = 1, 2, \dots ‚ m_{1}) \\ \underline{h}_{i} \leq h_{i} (X) & (i = 1, 2, \dots ‚ m_{2}) \\ \underline{w}_{i} \leq w_{i} (X) \leq \bar{w}_{i} & (i = 1, 2, \dots ‚ m_{3}) \\ \underline{x}_{i} \leq x_{i} \leq \bar{x}_{i} & (i = 1, 2, \dots ‚ n) \end{matrix} \end{array}} (1)$

这里, f为目标函数, X为设计变量, g_i, h_i, w_i为状态变量。

使用一阶分析法将有约束的多变量非线性规划问题变成无约束的非线性规划问题, 即将原目标函数f (X) 增广为一个新的函数:

$\begin{array}{l} Q (X ‚ q) = \frac{f}{f_{0}} + \sum_{i = 1}^{n} Ρ_{x} (x_{i}) + \\ q [\sum_{i = 1}^{m_{1}} Ρ_{g} (g_{i}) + \sum_{i = 1}^{m_{2}} Ρ_{h} (h_{i}) + \sum_{i = 1}^{m_{3}} Ρ_{w} (w_{i})] (2) \end{array}$ $\begin{array}{l} Q (X ‚ q) = \frac{f}{f_{0}} + \sum_{i = 1}^{n} Ρ_{x} (x_{i}) + \\ q [\sum_{i = 1}^{m_{1}} Ρ_{g} (g_{i}) + \sum_{i = 1}^{m_{2}} Ρ_{h} (h_{i}) + \sum_{i = 1}^{m_{3}} Ρ_{w} (w_{i})] (2) \end{array}$

式中f₀为参考目标函数, q为控制约束的参数。P_x为设计变量的外罚函数, P_g, P_h, P_w为状态变量的混合罚函数。

计算迭代步骤采用以下方法:

$X^{(j + 1)} = X^{(j)} + s_{j} d^{(j)} (3)$ $X^{(j + 1)} = X^{(j)} + s_{j} d^{(j)} (3)$

式中s_j是采用黄金分割法和最小二乘法来确定的参数, 其对应的搜索方向d^(j)可由Polak-Ribiere递推公式得到^[5]:

$\begin{array}{l} d^{(j)} = - Δ Q (X^{(j)} ‚ q_{k}) + r_{j - 1} d^{(j - 1)} (4) \\ r_{j - 1} = \\ \frac{[Δ Q (X^{(j)} ‚ q) - Δ Q (X^{(j - 1)} ‚ q)]^{Τ} Δ Q (X^{(j)} ‚ q)}{| Δ Q (X^{(j - 1)} ‚ q) |^{2}} (5) \\ \frac{\partial Q (X^{(j)})}{\partial x_{i}} \approx \frac{Q (X^{(j)} + Δ x_{i} e) - Q (X^{(j)})}{Δ x_{i}} (6) \end{array}$ $\begin{array}{l} d^{(j)} = - Δ Q (X^{(j)} ‚ q_{k}) + r_{j - 1} d^{(j - 1)} (4) \\ r_{j - 1} = \\ \frac{[Δ Q (X^{(j)} ‚ q) - Δ Q (X^{(j - 1)} ‚ q)]^{Τ} Δ Q (X^{(j)} ‚ q)}{| Δ Q (X^{(j - 1)} ‚ q) |^{2}} (5) \\ \frac{\partial Q (X^{(j)})}{\partial x_{i}} \approx \frac{Q (X^{(j)} + Δ x_{i} e) - Q (X^{(j)})}{Δ x_{i}} (6) \end{array}$

对于初始迭代步骤, 可令 $d^{(0)} = - Δ Q (X^{(0)} ‚ q)$ $d^{(0)} = - Δ Q (X^{(0)} ‚ q)$ 。最优化计算的收敛性采用式 (7) 来检验:

$| f^{(j)} - f^{(j - 1)} | \leq τ (7)$ $| f^{(j)} - f^{(j - 1)} | \leq τ (7)$

《2.2结构计算模型》

2.2结构计算模型

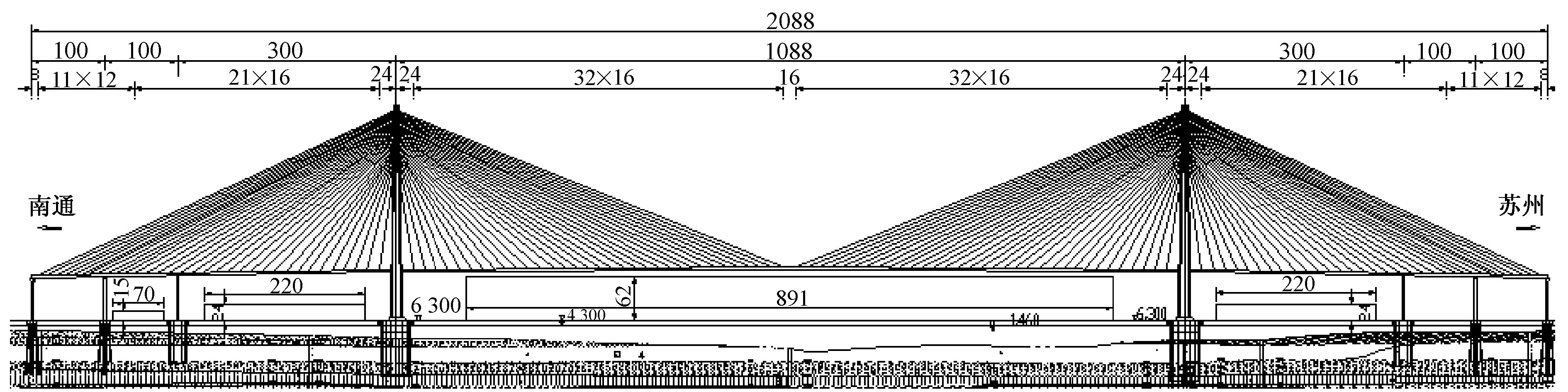
笔者的研究对象为长江口处正在规划建设的一座千米级斜拉桥。该桥主跨为1 088 m, 边跨为100+100+300 m, 总体布置如图1。边跨设两个辅助墩, 全漂浮体系;索塔为倒Y型钢筋混凝土塔, 承台以上塔高为297.7 m;塔柱为单箱单室断面, 桥面以上顺桥向宽9～13.5 m, 横桥向宽8～10 m;下塔柱顺桥向宽度13.5～15 m, 横桥向宽度7～8 m;索塔下横梁高度为8 m;主梁为钢箱结构, 梁高4.0 m, 全宽为40.6 m, 采用Q345C钢材全焊连接的封闭扁平流线型钢箱梁;斜拉索采用低松弛、高强度平行镀锌钢丝束, 边跨索距为10 m, 16 m, 中跨索距为16 m;斜拉索横向吊点间距为35.4 m, 全桥共设4×34对斜拉索。为平衡索塔水平力、优化桥梁整体受力及克服支座负反力, 在边跨三个辅助墩上部的主梁20 m, 25 m, 16 m范围内进行压重处理, 压重分别按45 t/m, 59 t/m, 54 t/m考虑;二期恒载按全桥7 t/m考虑。

《图1》

图1 某千米级斜拉桥方案立面图

Fig.1 The general view of a thousand-meter scale cable-stayed bridge

以往的斜拉桥合理恒载索力分析通常是按平面杆系进行的, 但是, 本桥属特大跨度, 桥梁的横向刚度相对较低, 由于双索面斜拉索抵抗扭转的原故及主梁中横梁的作用, 必须对主桥结构做三维空间分析。空间仿真分析须采用大型空间有限元程序, 该程序须具有多种单元混合计算功能, 能够考虑大变形几何非线性、材料非线性、构件安装拆卸等施工过程。目前国际上能直接满足上述要求的计算机程序几乎没有, 但是信誉较高的通用大型有限元程序倒有多个, 典型的是ANSYS, NASTRAN, ABAQUS等, 通过再开发可适应本桥的计算要求。

考虑到模型几何和荷载的对称性, 计算模型取结构的1/2进行分析。对自由扭转刚度较大的闭口钢箱梁断面, 选用“鱼骨”模式。主梁用位于其扭转中心的空间梁单元模拟;主梁的抗弯、抗扭刚度完全集中在这组梁单元中;主梁与斜拉索的联系通过主梁横向伸出的准刚性梁单元与斜拉索单元的连接来模拟, 计算模式如同“鱼骨”, 如图2所示。

《图2》

图2 结构离散图

Fig.2 Structural model

将主梁分成141个单元、142个节点;将索塔分成83个单元、83个节点;将斜拉索分成136个单元, 一根索一个单元。索塔和主梁均采用高精度的组合梁单元来模拟 (部分主梁、主塔的组合截面如图3所示) , 斜拉索用索单元来模拟。结构的自重按静力等效原则由计算机自动处理为等效结点力作用在相应结点上。结构的一些永久细部构造重也转换为集中结点荷载, 施加在相应结点上。约束条件是:塔底与承台固结, 施工阶段梁与塔中横梁临时固接, 辅助墩均为纵向活动、竖向约束铰支承, 在跨中的约束条件为纵向和面内转动约束、竖向和面外转动活动。根据斜拉桥的实际悬臂拼装过程, 在主梁和主塔各单元截面的积分点施加不同的初始应力, 来考虑结构在施工期间形成的初应力对结构后期承载能力的影响。

《2.3结构的几何非线性》

2.3结构的几何非线性

对于特大跨度斜拉桥, 必须计入以下几何非线性因素的影响:

1) 索的垂度影响

由于斜拉索总是存在自重, 所以在两端拉力的作用下, 拉索的变形由两部分组成:一部分是拉索材料应变引起的弹性变形;另一部分是拉索自重引起的几何形状改变, 即自重垂度。材料在弹性工作范围内, 弹性变形与所受的拉力成线性关系, 但自重垂度与索力成非线性关系。正是这种非线性关系, 使得拉索拉力与位移成非线性关系。考虑这种非线性影响的方法是对拉索的材料弹性模量进行修正, 即假想一个弹性模量, 使这个假想的弹性模量能够反映索的实际刚度, 即能反映由材料应变引起的弹性变形与由自重垂度引起的几何非线性变形之和。根据这一思想推出的假想弹性模量, 称为等效弹性模量。对于小跨径的斜拉桥, 规范中推荐使用的是切线模量法, 即Ernst公式。这种方法对于拉索长度为96 m、应力比为0.5以及拉索长度为250 m、应力比为0.8的情况, 误差将达2%^[6]。对于200 m以上的斜拉索, 必须对Ernst公式进行修正。为此, 笔者采用式 (8) 的割线模量法来考虑拉索的垂度影响:

《图3》

《图4》

图3 部分主梁、主塔的组合截面

Fig.3 Some combined sections of girder and cable tower

$\frac{1}{E_{e q}} = \frac{1}{E} + \frac{γ^{2} a^{2}}{24} (\frac{σ_{1} + σ_{2}}{σ_{1}^{2} σ_{2}^{2}}) (8)$ $\frac{1}{E_{e q}} = \frac{1}{E} + \frac{γ^{2} a^{2}}{24} (\frac{σ_{1} + σ_{2}}{σ_{1}^{2} σ_{2}^{2}}) (8)$

式中E_eq为等效弹性模量;γ是拉索材料的密度;σ₁, σ₂为迭代分析中最终和初始缆索应力;a为拉索长度的水平投影。

实践表明, 采用割线模量法, 当拉索长度在300 m以下时误差保持在1 %以下;拉索长度达到750 m时, 误差不到2 %。考虑到拉索本身弹性模量的误差约在2 %～3 %, 故对于实际应用而言, 割线模量法可满足要求^[6]。

拉索弦向力T与工程中实测得到的拉索上端索轴力N_B的换算关系为

$\frac{Ν_{B}}{Τ} = (\sqrt{4 - \frac{γ^{2} a^{2}}{σ^{2}}} + \frac{γ}{σ} h) (2 - \frac{γ^{2} (a^{2} + h^{2})}{2 σ^{2}})^{- 1} (9)$ $\frac{Ν_{B}}{Τ} = (\sqrt{4 - \frac{γ^{2} a^{2}}{σ^{2}}} + \frac{γ}{σ} h) (2 - \frac{γ^{2} (a^{2} + h^{2})}{2 σ^{2}})^{- 1} (9)$

式中N_B=aσ, 对于竖向投影在160 m以下的拉索, N_B与T间之差保持在1 %以下^[6];h为拉索长度的竖直高度。

采用割线弹性模量计入垂度效应时, 第一轮计算斜拉索的弹性模量用i-1阶段的索力对索弹性模量进行修正后作为第i阶段的模量, 以后各轮迭代, 利用上一轮相应阶段索力, 用于本阶段弹模修正计算。

2) 梁柱效应

斜拉桥主梁、主塔都工作在压弯状态, 引起了梁柱效应。应用梁单元分析时, 可以用稳定函数表示的几何非线性刚度矩阵或一般的几何刚度阵来计入这一效应。

3) 大位移效应

由于斜拉桥具有柔性结构特征, 外荷载作用下结构变形较大, 必须在变形后的位置建立平衡方程。可以用大位移刚度矩阵或基于U.L列式的有限位移理论计入这一效应。

《3 合理恒载索力分析》

3 合理恒载索力分析

《3.1合理成桥状态的确定原则[7]》

3.1合理成桥状态的确定原则[7]

1) 索力分布

索力既要分布均匀, 又要有较大的灵活性。通常短索的索力小, 长索的索力大, 呈递增趋势, 但局部地方应允许索力有突变。如0号索 (全漂浮体系的桥型时) 和1号索的索力通常用较大的值。在所有的索中, 不宜有太大或太小索力的索。

2) 主梁弯矩

主梁弯矩通常是混凝土斜拉桥设计中的难点和重点。在成桥状态下, 主梁的恒载弯矩要控制在“可行域”范围内。

3) 主塔弯矩

在恒载状态下, 主塔弯矩应考虑活载和混凝土后期收缩徐变的影响。在活载作用下, 塔往江侧的弯曲程度比岸侧大, 并且混凝土后期收缩徐变的影响往往使塔往江侧偏。因此, 在成桥恒载状态下, 塔宜向岸侧有一定的预偏。

4) 边墩和辅助墩支承反力

边墩和辅助墩支座反力在恒载下要有足够的压力储备, 最好在活载下不出现负反力。这种受力通常由配重或设置拉力支座来满足。

《3.2目标函数和约束条件》

3.2目标函数和约束条件

1) 目标函数

根据3.1节合理成桥状态的确定原则, 可将成桥状态下主梁和主塔的最小弯曲应变能设为目标函数, 经过最优化搜索计算, 建立起设计变量、状态变量与目标函数之间的函数关系, 求取目标函数的最小值。成桥后, 主梁与主塔的弯曲应变能为

$Q (x) = \sum_{i = 1}^{n} \int_{s} \frac{Μ}{E Ι} d s,$ $Q (x) = \sum_{i = 1}^{n} \int_{s} \frac{Μ}{E Ι} d s,$

其中n为主梁和主塔弯曲应变能计算构件数, I为构件组合截面的抗弯惯性矩, M为构件的弯矩, E为材料的压弯弹性模量。

2) 设计变量

将斜拉索索力设置为设计变量。全桥共有68个设计变量, 中跨和边跨拉索各34个。斜拉索的索力在成桥状态及运营过程中, 考虑到强度和疲劳问题, 应约束索力的上下极限值。给设计变量施加的约束条件为T_down≤T_j1, T_j2, …, T_j34≤T_up (中跨索力) , T_down≤T_a1, T_a2, …, T_a34≤T_up (边跨索力) 。

3) 状态变量

在进行斜拉桥恒载索力分析时, 如果单一采用结构应变能最小原理, 只能保证结构总体应变能最小, 不能保证所有控制内力和位移的设计要求, 故必须通过附加约束条件达到总体与局部的最佳平衡。同时, 计算构件的应变能是否作为优化的目标, 取决于结构受力特点和设计要求, 如斜拉桥一般可先只考虑主梁与塔的弯曲应变能, 通过初步计算再决定对索力和位移等附加约束条件。

钢箱主梁控制截面的应力、主塔的应力均是欲约束的变量, 可以将它们设置为状态变量, 其中钢箱梁的应力不宜大于200 MPa;边墩和辅助墩支承反力应确保大于零。

《3.3结果分析》

3.3结果分析

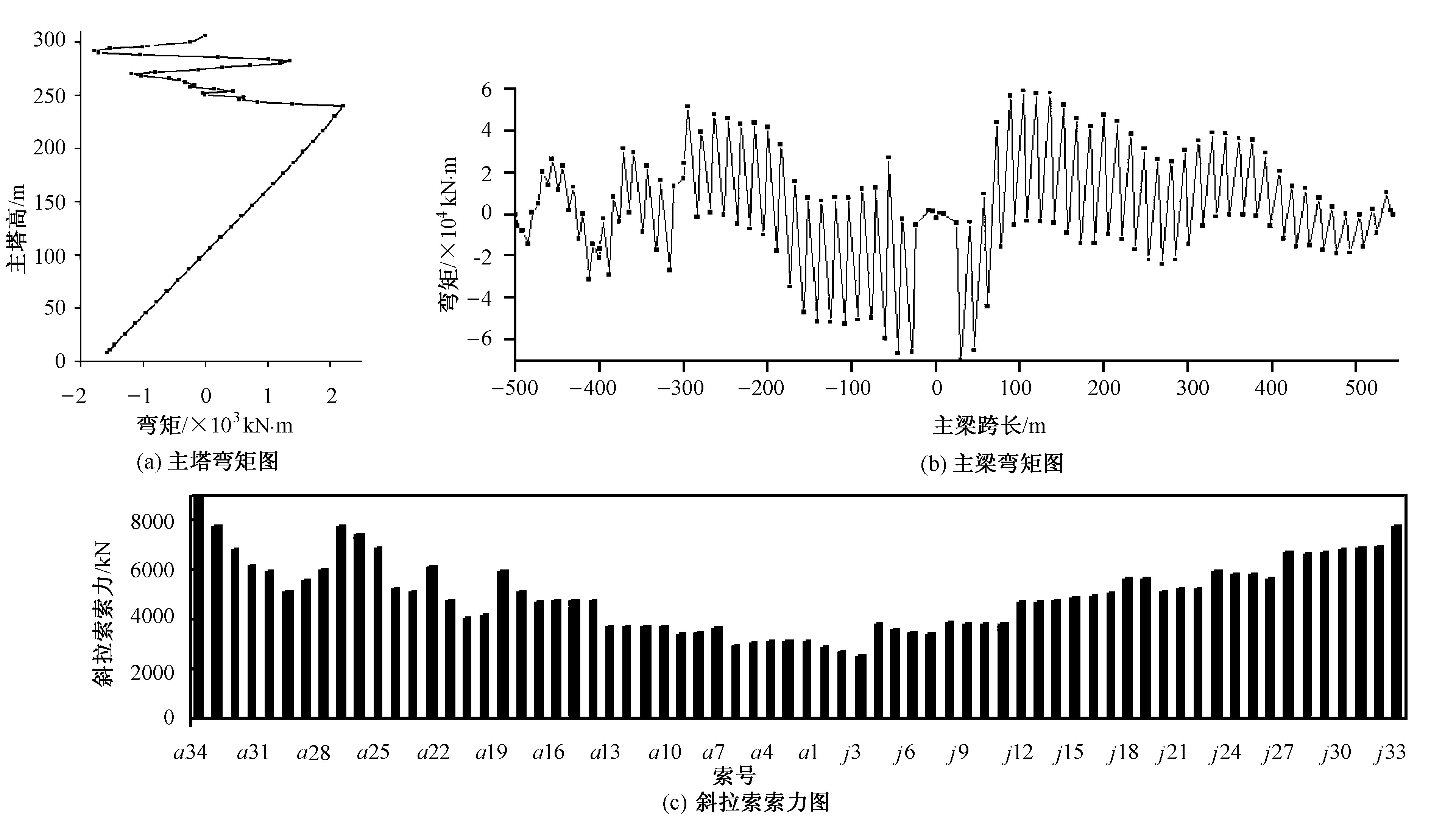
根据以上思路, 针对千米级斜拉桥的受力特点, 对ANSYS程序进行了二次开发, 利用APDL语言的迭代算法和UPFs语言的用户可编程特性, 开发了超长斜拉索模拟、斜拉索索力 (指定受力大小) 多次张拉模拟、临时和辅助墩只能受压不能受拉的支撑情况模拟等数十个子程序。运用编制的计算机仿真分析程序, 对千米级别长江大桥成桥状态下的索力进行分析。预先假设斜拉索的预张拉力为零, 对设计变量采用一阶分析法进行搜索计算, 从头到尾反复试算直到主塔和主梁的弯曲应变能最小为止。一阶方法使用因变量对设计变量的偏导数, 每次迭代都有一系列的子迭代 (包括搜索方向和梯度计算) 组成。这样一般经过10～15次迭代即可使计算结果收敛, 计算迭代步骤如图4。优化前 (斜拉索无初始张拉力) 主塔和主梁的弯矩、相应的斜拉索索力如图5。优化后主塔和主梁的弯矩、相应的斜拉索索力如图6。

计算结果显示, 优化前主梁控制结点的总弯矩为5.675×10⁶ kN·m;优化后主梁控制结点的总弯矩为2.956×10⁶ kN·m, 为优化前的52 %。优化前主塔控制结点的总弯矩为8.018×10⁷ kN·m;优化后主塔控制结点的总弯矩为1.975×10⁵ kN·m, 只有优化前的0.2 %。图6显示, 当主塔塔高超过200 m后, 由于边跨和中跨索力水平分力的不平衡, 引起主塔索梁锚固区的弯矩值有比较大的突变。由于图5横坐标的尺度比图6大100倍, 该区域内弯矩值突变显示并不明显。优化后, 单根最大恒载索力发生在边跨第34号索, 为8 990.9 kN;最小恒载索力发生在中跨第4号索, 为2 542.9 kN。拉索张力分布规律也与普通斜拉桥规律类似, 最大拉力发生在边跨端点处与跨中附近。

《图5》

图4 目标函数与迭代次数

Fig.4 The objective function and number of iteration

《图6》

图5 实际状态弯矩及斜拉索索力

Fig.5 The bending moment and cable forces before optimization

采用这种计算方法, 可使结构的弯曲能量大为减小, 且迭代收敛速度快。这表明一阶分析法用于确定斜拉桥的合理成桥状态是有效的。

《4 结论》

4 结论

通过对千米级斜拉桥的合理成桥状态进行分析, 得到以下主要结论:

1) 采用一阶分析法求解有约束的最优化问题, 计算表明, 此方法计算精度高, 且收敛速度快, 可由初始可行方案经过优化计算得到最优点, 这是一种重要的方法。它借助于结构有限元分析、结构设计灵敏度分析、可行方向法以及对偶单纯形算法, 进行反复选代计算直至获得结构的最优设计, 这一方法适用于多单元、多工况、多设计变量的斜拉桥优化设计非线性规划问题的求解。其中, 有限元分析法用于计算结构的位移和应力, 可确定每一约束条件是否临界;结构的灵敏度分析目的是确定约束函数的导数;而可行方向法则是优化过程的主体。优化迭代时用户可任意指定收敛精度与迭代次数, 不会由于在所要求的约束上下界范围内无可行解而造成算法失败。

《图7》

图6 优化状态弯矩及斜拉索索力

Fig.6 The bending moment and cable forces in the optimization state

2) 将一阶分析法最优化计算理论引入斜拉桥合理成桥状态的确定是可行的, 结果是合理的。该方法可以考虑结构的非线性影响, 满足斜拉桥调索过程中对索力、位移、弯矩等不同性态的约束, 只需经过简单的几个迭代计算, 即可获得精确的解。

3) 以斜拉桥主梁和索塔的弯曲应变能为目标函数的索力优化方法, 可全面反映全桥结构对斜拉索初张力的响应, 使优化结果更为合理。

4) 对于千米级斜拉桥, 斜拉索垂度、梁柱效应及大挠度引起的整体结构几何非线性是明显的。通过对斜拉索弹性模量的修正, 引入初始应力矩阵, 可以方便有效地考虑上述非线性因素的影响。

展示更多