基于Lagrange方程建模的单级旋转倒立摆控制

摘要

介绍一种新型单级旋转倒立摆系统的构成，通过对其动力学特性的分析建立了基于Lagrange方程的数学模型。在平衡点附近给出系统的线性化模型，对系统的稳定性、能控性和能观性进行了分析。利用线性二次型最优控制策略LQR方法设计了控制器，并在仿真实验和实物实验中实现了倒立摆的平衡控制。实验表明，系统稳定性好、鲁棒性较强。

正文

《1 引言》

1 引言

倒立摆 (IP, inverted pendulum) 是一个复杂的快速、非线性、多变量、强耦合、自然不稳定的非最小相位系统, 是重心在上、支点在下控制问题的抽象。目前在对倒立摆问题的研究中, 以小车式倒立摆为控制对象的文章很多^[1,2,3]。但是, 小车式倒立摆在机械系统上需要有很长的导轨, 这占用了较大的空间。另外, 由于小车式倒立摆有着繁多的传动机构, 在实验过程中经常因为机械系统的误差和故障影响控制效果, 从而干扰对控制算法本身性能的有效判断。

旋转式倒立摆与小车式倒立摆不同, 由于将小车的平动控制改为旋臂的旋转控制, 在硬件结构上减少了中间传动机构, 相对于小车式倒立摆具有更大的非线性、不稳定性和复杂性, 对控制算法提出了更高的要求。

笔者研究的是一种新型的旋转倒立摆装置, 设计了基于Lagrange方程建模的单级旋转倒立摆控制系统, 控制效果良好。

《2 旋转倒立摆的控制系统结构》

2 旋转倒立摆的控制系统结构

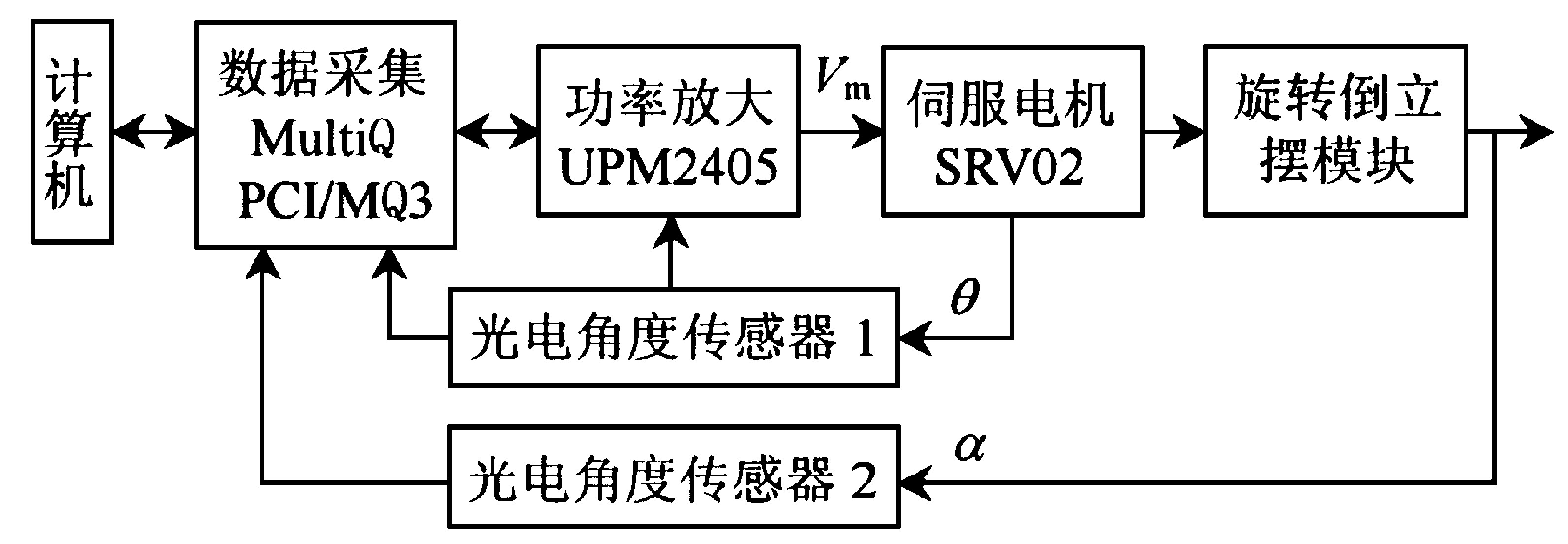
笔者使用的单级旋转倒立摆控制系统结构如图1所示。系统包括PC机、数据采集卡MultiQ PCI/MQ3、功率放大器UPM 2405、直流伺服电动机SRV02、单级旋转倒立摆和光电角度传感器等几部分, 组成了一个单级旋转倒立摆闭环控制系统。

《图1》

图1 单级旋转倒立摆控制系统结构

Fig.1 The structure of single link rotaryinverted pendulum control system

其中, 控制器输入为旋臂相对零位的转角θ和摆杆相对零位的转角α;控制器输出为直流伺服电机的电枢电压V_m。因此, 该系统是一个双输入单输出闭环控制系统。

作为系统的控制对象, 单级旋转倒立摆由连接在直流伺服电机转轴上的水平旋臂和可自由摆动的摆杆组成, 旋臂和摆杆之间以铰链相连接。倒立摆系统具有2个自由度, 旋臂为定轴转动, 摆杆为空间一般运动。

由于受到铰链的作用, 倒立摆杆只能沿圆周的切线方向摆动。此时, 铰链上和直流电机转轴上的角位移传感器将检测到的角位移量, 经过数据采集卡的A/D转换送入控制计算机。由计算机通过特定的控制算法给出控制电压信号, 再经过数据采集卡的D/A转换以及功率放大器放大后加载于直流伺服电机, 驱动旋臂在水平面内转动, 从而使摆杆保持倒立平衡姿态。

《3 系统数学模型的建立》

3 系统数学模型的建立

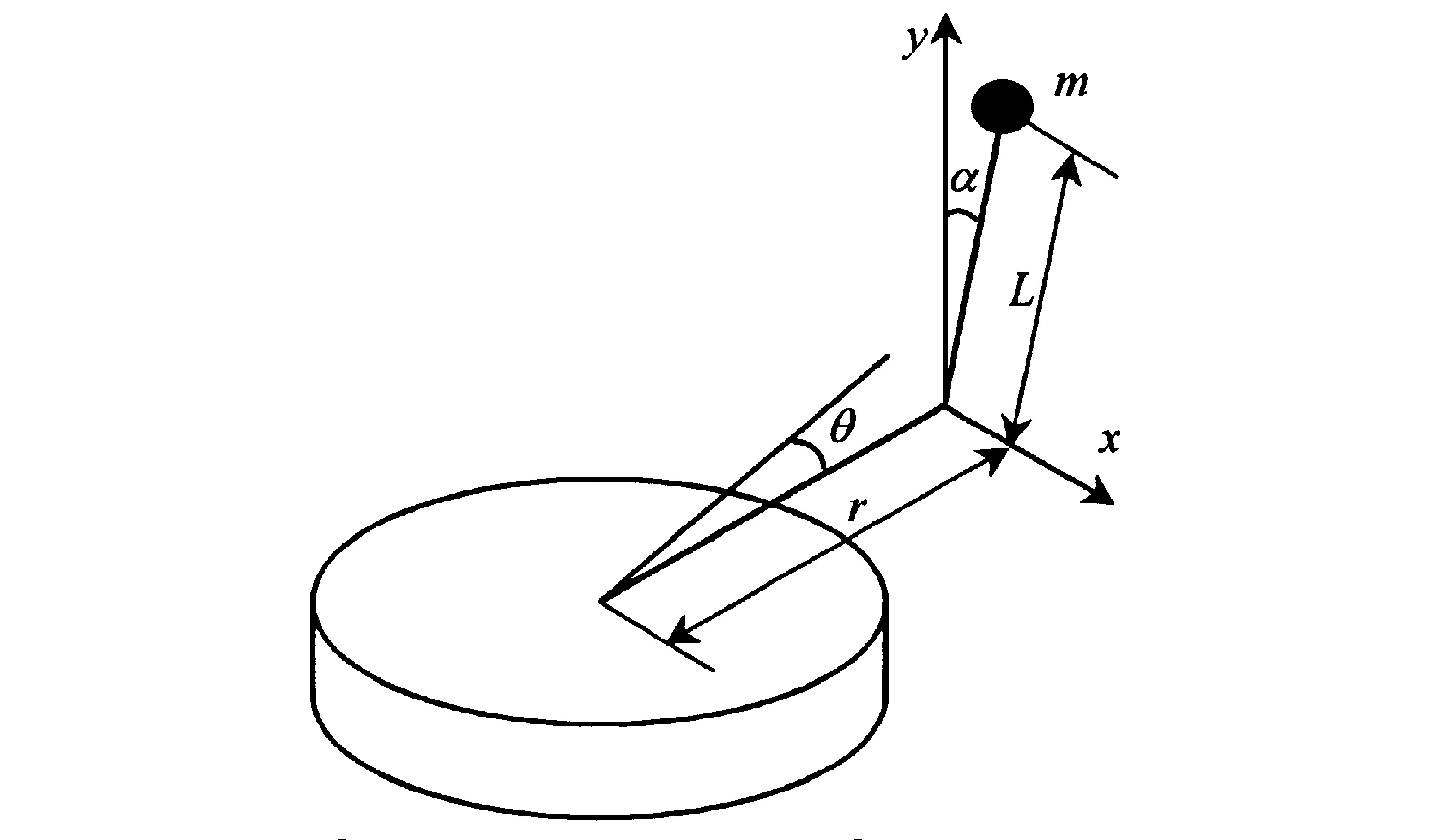
对旋转倒立摆系统建立数学模型是实现倒立摆控制的基础, 下面对实验采用的单级旋转倒立摆系统的数学模型进行分析。如图2所示, 在忽略各种阻力和摩擦的条件下, 旋臂和摆杆可以抽象为的2个匀质杆, 其中旋臂长度为r, 相对其水平方向零位的角位移为θ;摆杆质心与铰链距离为L, 相对其竖直方向零位的角位移为α。

《图2》

图2 系统模型分析

Fig.2 Analysis of the system model

由动力学理论, 摆杆质心在x方向和y方向的速度分量为^[4]:

$\begin{array}{l} V_{x} = r \dot{θ} - L c o s α (\dot{α}) ‚ \\ V_{y} = - L s i n α (\dot{α}) (1) \end{array}$ $\begin{array}{l} V_{x} = r \dot{θ} - L c o s α (\dot{α}) ‚ \\ V_{y} = - L s i n α (\dot{α}) (1) \end{array}$

方程组式 (1) 给出了完整的摆杆速度描述, 应用Lagrange方程可推导出系统的动态方程。

以旋臂所在水平面为零势能面, 则系统的势能为摆杆的重力势能:V=mgLcosα。系统的动能由4部分构成, 包括:旋臂在水平面内的转动, 摆杆在竖直平面内的转动, 摆杆质心沿x轴方向的速度、沿y轴方向的速度。对应的动能分量分别用T₁, T₂, T₃, T₄表示, 因此系统动能T为四者之和, 即T=T₁+T₂+T₃+T₄, 其中 $Τ_{1} = J_{1} \dot{θ}^{2} / 2 ‚ Τ_{2} = J_{2} \dot{α}^{2} / 2$ $Τ_{1} = J_{1} \dot{θ}^{2} / 2 ‚ Τ_{2} = J_{2} \dot{α}^{2} / 2$ , $Τ_{3} = m (r \dot{θ} - L \cos α (\dot{α})^{2}) / 2$ $Τ_{3} = m (r \dot{θ} - L \cos α (\dot{α})^{2}) / 2$ , $Τ_{4} = m (- L c o s α (\dot{α}))^{2} / 2 。$ $Τ_{4} = m (- L c o s α (\dot{α}))^{2} / 2 。$ 所以系统动能为

$\begin{array}{l} Τ = J_{1} \dot{θ} / 2 + J_{2} \dot{α}^{2} / 2 + m (r \dot{θ} - L c o s α (\dot{α}))^{2} / 2 + \\ m (- L c o s α (\dot{α}))^{2} / 2 (2) \end{array}$ $\begin{array}{l} Τ = J_{1} \dot{θ} / 2 + J_{2} \dot{α}^{2} / 2 + m (r \dot{θ} - L c o s α (\dot{α}))^{2} / 2 + \\ m (- L c o s α (\dot{α}))^{2} / 2 (2) \end{array}$

设R为摆杆长度, 由于L为R的一半, 即R=2L。因此, 摆杆对质心的转动惯量为J₂=mR²/12=mL²/3。将J₂代入式 (2) , 可推导出Lagrange函数

$\begin{array}{l} L = Τ - V = J_{1} \dot{θ}^{2} / 2 + 2 m L^{2} \dot{α}^{2} / 3 - \\ m L r c o s α (\dot{α}) (\dot{θ}) + m r^{2} \dot{θ}^{2} / 2 - m g L c o s α 。 \end{array}$ $\begin{array}{l} L = Τ - V = J_{1} \dot{θ}^{2} / 2 + 2 m L^{2} \dot{α}^{2} / 3 - \\ m L r c o s α (\dot{α}) (\dot{θ}) + m r^{2} \dot{θ}^{2} / 2 - m g L c o s α 。 \end{array}$

应用Lagrange方程 $L (q, \dot{q}) = Τ (q, \dot{q}) - V (q, \dot{q})$ $L (q, \dot{q}) = Τ (q, \dot{q}) - V (q, \dot{q})$ , 其中L为拉格朗日算子, q为系统的广义坐标, T为系统的动能, V为系统的势能。Lagrange方程由广义坐标q_i和L表示为

$\frac{\partial}{\partial t} (\frac{\partial L}{\partial q_{i}}) - \frac{\partial L}{\partial q_{i}} = f_{i} 。$ $\frac{\partial}{\partial t} (\frac{\partial L}{\partial q_{i}}) - \frac{\partial L}{\partial q_{i}} = f_{i} 。$

在系统中, i=1, 2, q={θ, α}, f_i为系统沿该广义坐标方向上的外力, 可得方程组

$\begin{array}{l} \frac{\partial}{\partial t} (\frac{\partial L}{\partial \dot{θ}}) - \frac{\partial L}{\partial θ} = Τ_{o u t p u t} - B_{e q} \dot{θ} ‚ \\ \frac{\partial}{\partial t} (\frac{\partial L}{\partial \dot{α}}) - \frac{\partial L}{\partial α} = 0 ‚ \end{array}$ $\begin{array}{l} \frac{\partial}{\partial t} (\frac{\partial L}{\partial \dot{θ}}) - \frac{\partial L}{\partial θ} = Τ_{o u t p u t} - B_{e q} \dot{θ} ‚ \\ \frac{\partial}{\partial t} (\frac{\partial L}{\partial \dot{α}}) - \frac{\partial L}{\partial α} = 0 ‚ \end{array}$

其中T_output为直流伺服电机的输出转矩,

$Τ_{o u t p u t} = η_{m} η_{g} Κ_{i} Κ_{g} (V_{m} - Κ_{g} Κ_{m} θ) / R_{m}$ $Τ_{o u t p u t} = η_{m} η_{g} Κ_{i} Κ_{g} (V_{m} - Κ_{g} Κ_{m} θ) / R_{m}$

在平衡点 $(θ \dot{θ} α \dot{α})^{Τ} = (0 0 0 0)^{Τ}$ $(θ \dot{θ} α \dot{α})^{Τ} = (0 0 0 0)^{Τ}$ 附近, 假设θ和α同1 rad相比很小, 即θ≪1, α≪1, 则方程组可局部线性化为

$\begin{array}{l} (J_{1} + m r^{2}) \ddot{θ} - m L r \ddot{α} = Τ_{o u t p u t} - B_{e q} \ddot{θ}, \\ 4 m L^{2} \ddot{α} / 3 - m L r \ddot{θ} - m g L α = 0 (3) \end{array}$ $\begin{array}{l} (J_{1} + m r^{2}) \ddot{θ} - m L r \ddot{α} = Τ_{o u t p u t} - B_{e q} \ddot{θ}, \\ 4 m L^{2} \ddot{α} / 3 - m L r \ddot{θ} - m g L α = 0 (3) \end{array}$

由方程组式 (3) , 代入上述相关参数, 可以写出单级旋转倒立摆系统的线性化状态方程为

$\begin{array}{l} [\begin{array}{l} \dot{θ} \\ \ddot{θ} \\ \dot{α} \\ \ddot{α} \end{array}] = [\begin{matrix} 0 & 1 & 0 & 0 \\ 0 & \frac{- 4 G}{4 J_{1} + m r^{2}} & \frac{3 r g}{4 J_{1} + m r^{2}} & 0 \\ 0 & 0 & 0 & 1 \\ 0 & \frac{- 3 r G}{(4 J_{1} + m r^{2}) L} & \frac{3 (J_{1} + m r^{2})}{(4 J_{1} + m r^{2}) L} & 0 \end{matrix}] [\begin{array}{l} θ \\ \dot{θ} \\ α \\ \dot{α} \end{array}] + \\ [\begin{matrix} 0 \\ \frac{4 η_{m} η_{g} Κ_{t} Κ_{g}}{(4 J_{1} + m r^{2}) R_{m}} \\ 0 \\ \frac{3 r η_{m} η_{g} Κ_{t} Κ_{g}}{(4 J_{1} + m r^{2}) L R_{m}} \end{matrix}] V_{m} (4) \end{array}$ $\begin{array}{l} [\begin{array}{l} \dot{θ} \\ \ddot{θ} \\ \dot{α} \\ \ddot{α} \end{array}] = [\begin{matrix} 0 & 1 & 0 & 0 \\ 0 & \frac{- 4 G}{4 J_{1} + m r^{2}} & \frac{3 r g}{4 J_{1} + m r^{2}} & 0 \\ 0 & 0 & 0 & 1 \\ 0 & \frac{- 3 r G}{(4 J_{1} + m r^{2}) L} & \frac{3 (J_{1} + m r^{2})}{(4 J_{1} + m r^{2}) L} & 0 \end{matrix}] [\begin{array}{l} θ \\ \dot{θ} \\ α \\ \dot{α} \end{array}] + \\ [\begin{matrix} 0 \\ \frac{4 η_{m} η_{g} Κ_{t} Κ_{g}}{(4 J_{1} + m r^{2}) R_{m}} \\ 0 \\ \frac{3 r η_{m} η_{g} Κ_{t} Κ_{g}}{(4 J_{1} + m r^{2}) L R_{m}} \end{matrix}] V_{m} (4) \end{array}$

其中G= (η_mη_gK_tK_mK²_g+B_eqR_m) /R_m

将系统各机械参数值代入式 (4) , 得单级旋转倒立摆系统的线性化数学模型如下

$\begin{array}{l} [\begin{array}{l} \dot{θ} \\ \ddot{θ} \\ \dot{α} \\ \ddot{α} \end{array}] = [\begin{matrix} 0 & 1 & 0 & 0 \\ 0 & - 14.52 & 39.32 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & - 13.98 & 81.78 & 0 \end{matrix}] [\begin{array}{l} θ \\ \dot{θ} \\ α \\ \dot{α} \end{array}] + [\begin{matrix} 0 \\ 25.54 \\ 0 \\ 24.59 \end{matrix}] V_{m} (5 a) \\ y = [1 0 1 0] [θ \dot{θ} α \dot{α}]^{Τ} (5 b) \end{array}$ $\begin{array}{l} [\begin{array}{l} \dot{θ} \\ \ddot{θ} \\ \dot{α} \\ \ddot{α} \end{array}] = [\begin{matrix} 0 & 1 & 0 & 0 \\ 0 & - 14.52 & 39.32 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & - 13.98 & 81.78 & 0 \end{matrix}] [\begin{array}{l} θ \\ \dot{θ} \\ α \\ \dot{α} \end{array}] + [\begin{matrix} 0 \\ 25.54 \\ 0 \\ 24.59 \end{matrix}] V_{m} (5 a) \\ y = [1 0 1 0] [θ \dot{θ} α \dot{α}]^{Τ} (5 b) \end{array}$

上述推导过程中各参数的物理意义和数值单位如表1所示。

表1 系统物理参数表

Table 1 The parameters of the system

《表1》

符号	物理意义	数值及单位
L	摆杆质心到转轴距离/m	0.165
M	摆杆质量/kg	0.105
R	旋臂长度/m	0.175
J₁	旋臂的转动惯量/kg·m²	2.0×10^-3
J₂	摆杆对质心转动惯量/kg·m²	9.53×10^-4
g	重力加速度/m·s^-2	9.8
V_x	摆杆质心x方向速度/m·s^-1
V_y	摆杆质心y方向速度/m·s^-1
θ	旋臂角位移/rad
$\dot{θ}$ $\dot{θ}$	旋臂角速度/rad·s^-1
α	摆杆角位移/rad
$\dot{α}$ $\dot{α}$	摆杆角速度/rad·s^-1
K_t	电机力矩系数/N·m·A^-1	7.767×10^-3
K_m	反向电势系数/V·s·rad^-1	7.767×10^-3
K_g	变速器齿轮比	5∶1
R_m	直流电机电枢电阻/Ω	2.6
V_m	直流电机电枢电压/V
η_m	直流电机效率/%	69
η_g	变速器效率/%	90
B_eq	粘性阻尼系数/N·ms·rad^-1	4.0×10^-3

由线性化数学模型得系统的特征值为λ₁=0, λ₂=-17.1209, λ₃=7.5407, λ₄=-4.9398。可见, λ₃ =7.5407位于复平面的右半平面, 系统在平衡点附近不稳定。因此, 单级旋转倒立摆为开环不稳定系统, 需要设计控制器来镇定系统。同样可以计算出系统的能控性、能观性矩阵的秩均为4, 因而系统能控、能观。下面的控制方案就是在上述状态空间线性模型的基础上进行的。

《4 旋转倒立摆的稳定控制》

4 旋转倒立摆的稳定控制

《4.1倒立摆系统的控制目标》

4.1倒立摆系统的控制目标

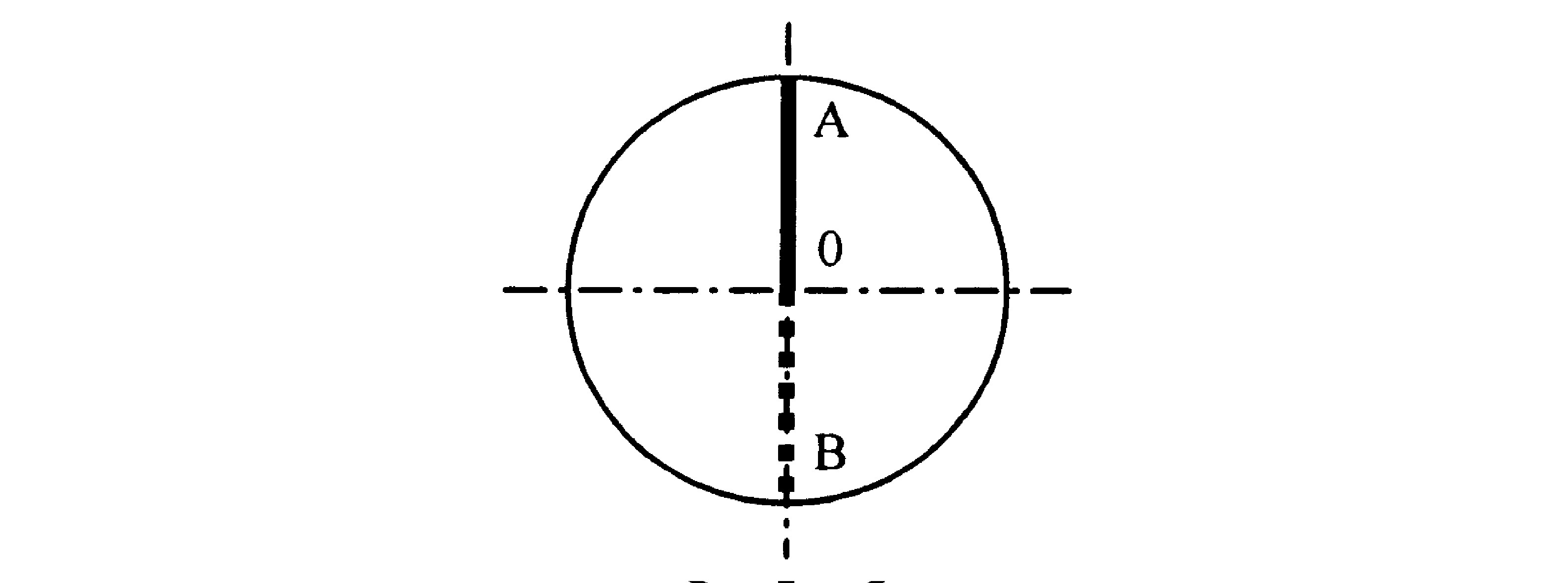
在倒立摆系统中, 摆杆的位置有竖直向上和竖直向下两种平衡状态。二者的区别是竖直向下的状态 (图3中B点) 是稳定的平衡点, 而竖直向上的状态 (图3中A点) 是不稳定的平衡点。在不施加控制作用的情况下, 只要施加微小的扰动就会使系统偏离平衡点A而振荡发散。在振荡过程中, 由于存在空气阻力和机械摩擦力, 系统将耗散能量, 因此摆杆最终将回复到稳定的平衡点B。倒立摆平衡状态的分析如图3所示。

《图3》

图3 倒立摆平衡状态分析

Fig.3 Analysis of the balance position

倒立摆的控制目标就是使倒立摆在不稳定的平衡点附近的运动成为一个稳定的运动。控制夹角α, θ在各自的零点附近变化, 而整个摆处于一种动态平衡, 要使摆静止在平衡位置是不可能的, 只能是在平衡位置处的振荡^[5]。

《4.2最优控制策略LQR控制器设计》

4.2最优控制策略LQR控制器设计

根据现代控制理论, 设最优控制量为U=-KX, 使得系统二次型性能指标

$J = \frac{1}{2} \int_{0}^{\infty} (X^{Τ} Q X + U^{Τ} R U) d t$ $J = \frac{1}{2} \int_{0}^{\infty} (X^{Τ} Q X + U^{Τ} R U) d t$

取最小。

利用Matlab提供的lqr () 函数可以方便地算出控制矩阵K, 选择合适的加权矩阵Q和R, 取Q=[2.3 45 0 0], R=1, 矩阵Q和R用来平衡系统对输入量和输出量的敏感程度。

计算得出, 最优状态反馈增益矩阵为

$Κ = [- 1.5166 - 14.8245 - 1.6098 - 1.5470] 。$ $Κ = [- 1.5166 - 14.8245 - 1.6098 - 1.5470] 。$

系统的闭环极点为-37.8150, -19.7852, -2.6226+1.2008i, -2.6226+1.2008i。可以看到, 系统4个极点均处于复平面的左半平面, 因此, 系统是镇定的^[6]。

《4.3仿真及实控实验结果》

4.3仿真及实控实验结果

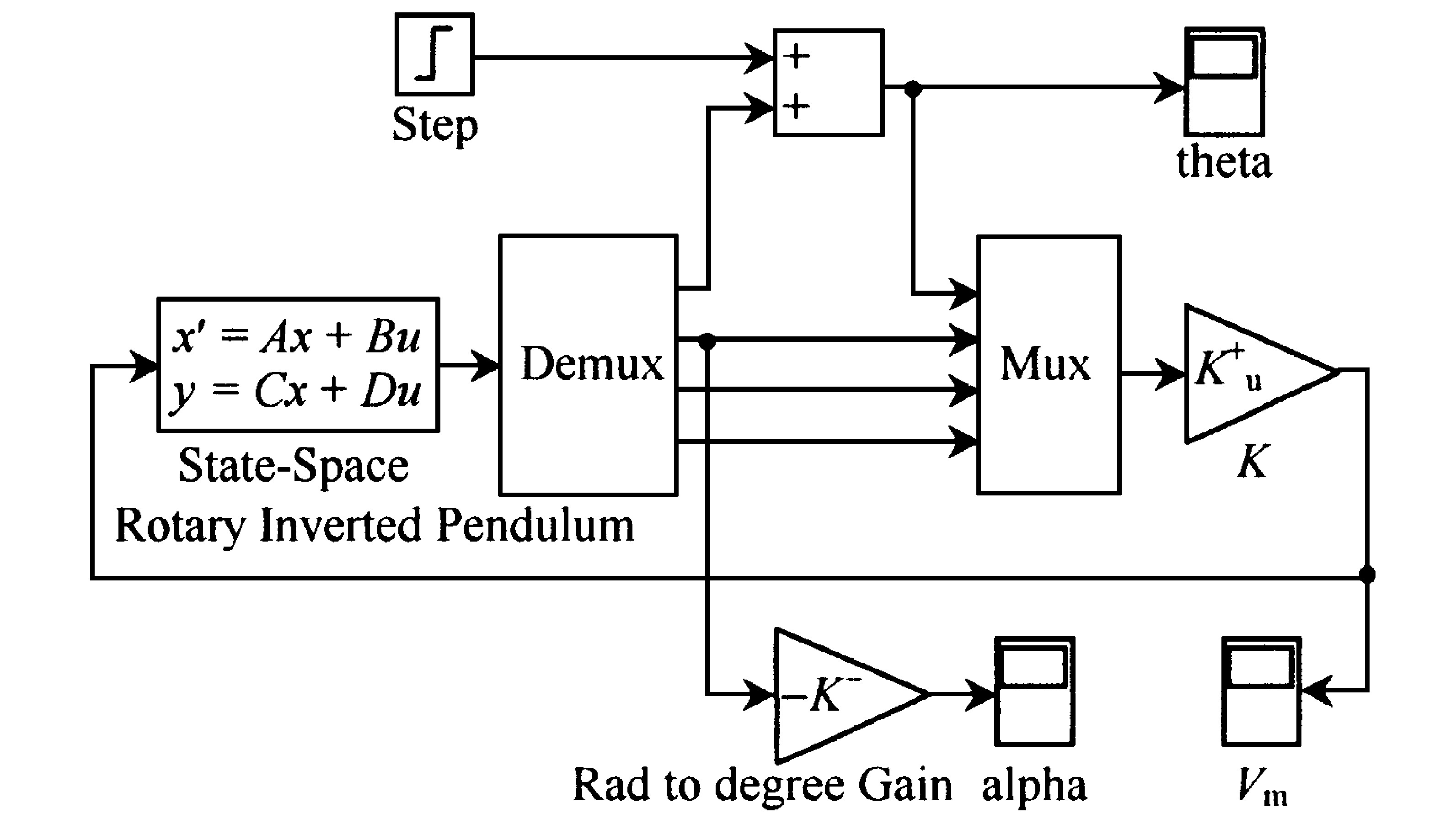
鉴于旋转式倒立摆的自然不稳定性, 以及出于对实验设备的保护, 不应直接在实验设备上进行调试。首先在Matlab的Simulink环境下进行仿真, 建立仿真模型 (如图4) 。

《图4》

图4 仿真系统结构图

Fig.4 The simulation system structure

系统仿真的阶跃响应曲线如图5所示, 图5中3条响应曲线, 从上至下依次为:摆杆角位移α、旋臂角位移θ和电枢电压V_m。在旋臂角位移θ的变化率 $\dot{θ}$ $\dot{θ}$ 为1 rad/min的阶跃输入下, 摆杆偏角α的最大超调量不超过±6°, 并在2 s内达到稳定。

《图5》

图5 系统仿真曲线

Fig.5 The system simulation curves

再对实际的旋转倒立摆系统进行实控, 主要考察倒立摆杆偏转角度α的控制曲线, 得到实验曲线如图6所示。

由图6中可以看出, 控制器开始工作后, 在控制器LQR的调节下, 倒立摆能够很好的稳定, 摆杆角度变化幅度不超过±1.5°。且在其摆动过程中可以接受在±10°的扰动力矩范围内保证倒立摆稳定振动, 控制系统的鲁棒性良好。

《图6》

图6 摆杆角度变化曲线

Fig.6 Tracking curves of the pole angle

在此基础上, 进一步检验控制系统的鲁棒性。在负责建立系统状态空间的Matlab程序中, 将摆杆质量参数增大1倍, 即由原来的0.105 kg 变为0.210 kg。这样, 系统状态空间中摆杆质量m与实际所用摆杆的质量0.105 kg已经不相符。利用重新计算的状态反馈增益矩阵K, 得到参数失配后的摆杆角度变化曲线, 如图7所示。

《图7》

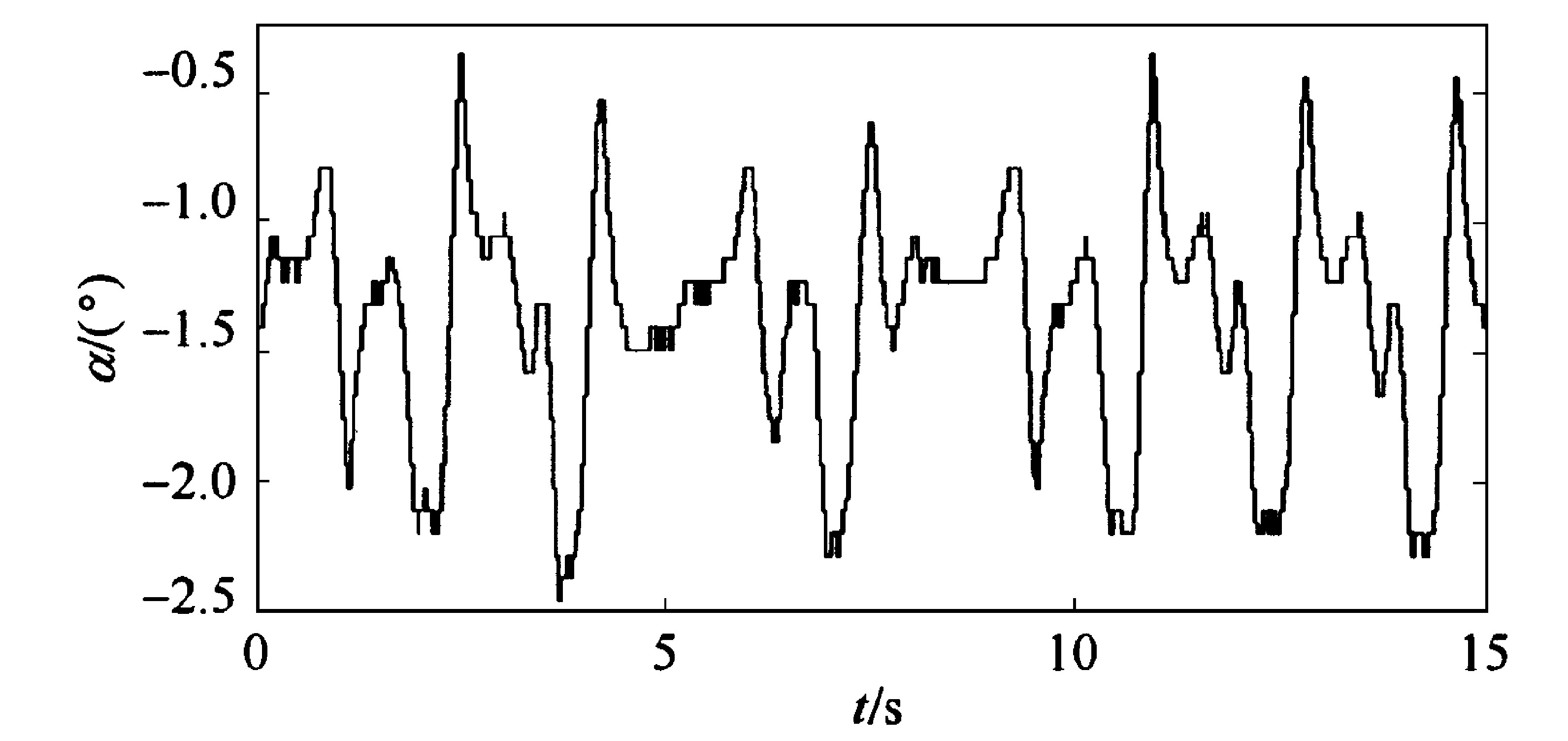
图7 参数失配后的角度变化曲线

Fig.7 Tracking curves of the pole angle on the condition of parameter matching error

实验结果显示, 摆杆仍能保持稳定的倒立平衡姿态。这说明虽然状态空间和状态反馈增益矩阵已经改变, 但控制器对系统参数的变化不敏感, 具有一定的自适应能力, 且鲁棒性较强。

从系统实控曲线图7中还可以看出:在对实际系统的控制中, 系统的平衡点并非处于零点。造成此现象的主要原因是, 在倒立摆启动的瞬间, 摆杆并非处于严格的竖直向上位置, 而是与竖直方向之间存在微小的倾角。控制器能够根据除摆杆偏转角α以外的其他3个状态变量的变化进行修正并找到准确的平衡点。

《5 结论》

5 结论

以单级旋转倒立摆为控制对象, 应用线性系统最优控制理论设计了LQR控制器, 由仿真及实控实验结果可以看出, 控制方法原理简单, 实现容易, 表现出较好的控制性能, 并在实际系统中实现了旋转倒立摆的稳定控制。

展示更多