基于TLBO算法的不确定性条件下复杂产品协同设计的可靠性拓扑优化

摘要

复杂产品的拓扑优化设计可以显著改善材料和节能，有效地降低惯性力和机械振动。本研究选择了一种大吨位液压机作为典型的复杂产品，用以表述这种优化方法。基于可靠性和优化解耦模型与基于教与学优化（TLBO）算法，本文提出了一种可靠性拓扑优化方法。将由板系结构形成的支撑物作为拓扑优化对象，具有轻量化和稳定性好的特点。将某种不确定性下的可靠性优化和结构拓扑优化协同处理。首先，利用有限差分法将优化问题中的不确定性参数修正为确定性参数。然后，将不确定性可靠性分析和拓扑优化的复杂嵌套解耦。最后，利用TLBO算法求解解耦模型。该算法参数少，求解速度快。TLBO算法采用了自适应教学因子，在初始阶段实现了更快的收敛速度，并在后期阶段进行了更精细的搜索。本文给出了一个液压机基板结构的数值实例，验证了该方法的有效性。

正文

《1、引言》

1、引言

复杂产品制造数量的激增，加剧了资源消耗和环境污染，对地球生态系统造成巨大的压力。例如，直到2018年，全球温室气体（GHG）的排放量仍持续上升[1]。2019年全球碳排放总量为330亿吨，温室气体放量增长略有放缓[2]。在复杂产品制造中，黑色金属冶炼和加工是温室气体排放的主要贡献者，其份额为35.9% [3]。液压机是金属成形过程中的主要设备，因为它们能够提供高压成型[4‒5]。然而，它们也是典型的复杂产品，在制造过程中会导致较高的能源消耗和材料成本。2013年，中国生产了约200万台金属成型机[6]。对能源和材料资源日益增长的需求可能会对环境造成不可逆转的破坏。因此，本研究主要关注复杂产品的设计优化、平衡性能和资源节约指标，以及以液压机为优化案例的研究。

许多研究者探索了液压机的优化方法，以降低资源成本和减轻环境污染。这些优化方法主要集中在驱动系统[7‒12]等的有效利用和合理的结构设计上。与传统的驱动系统优化相比，大型设备的结构优化是节约资源和减少消耗的关键。结构优化侧重于整个机器及其零部件的尺寸、重量、布局等。其中，液压机的轻量化设计优化不仅节省了资源，而且提高了液压机的性能。就满足可靠性要求而言，液压机的重量越大意味着金属材料的成本越高。此外，重型液压机具有较大的惯性，在运输或加工过程中往往会消耗更多的燃料。然而，合理的减重可以在保证恒定刚度的同时增加支架的固有频率，从而减少振动和更好地承重液压机。因此，正确确定支撑材料、壁厚、横截面形状和尺寸对合理制造板系结构很重要。Strano等[13]在能源效率方面优化了设计过程。Li等[14]为液压机采用了一种有效的拓扑优化器，以减少温室气体排放，并提高液压机在制造中的结构性能。Liu等[15]采用显式拓扑优化方法改进了液压机滑块的低碳铸造性能。

在液压机中，支撑件对保证工作的安全和稳定起着重要的作用。将由独立的板单元定制焊接或铸造所形成的板系结构视为基结构。该板系结构具有结构简单、易于制造、承载力大等优点。在目前的板系结构设计优化中，大多数支撑件是通过改变现有板系结构布局内的尺寸参数来优化的。这种设计优化的目的是减少结构的重量，但效果有限。与拓扑优化相比，单个组件的尺寸优化设计自由度较低，在有限的区域内不能显著降低重量。本文提出了一种协作拓扑优化方法，同时改变板单元的数量和优化它们的大小。与以往通过经验确定板系结构布局的方法相比，本文提出的新方法可以有效地降低整体重量，提高板系结构的支撑刚度。

拓扑优化的设计目标是板的厚度参数和拓扑变量。这些目标可以用一个基于桁架结构的数学模型来解决。在以往的研究中，许多研究人员研究了优化桁架结构的适用方法。有限元法（FEM）作为一种有效的传统优化方法经过了研究者的改进。他们使用有限元法来分析框架结构，并对最优设计参数进行了测试和评价[16‒19]。除了优化方法外，许多研究都集中在结构特征的性能上。Lan等[20]考虑了三个方面——拓扑结构、形状和尺寸——对精密冲裁压力机框架的设计进行优化。Yan等[21]基于有限元优化方法对液压机重型承重框架的特性进行了研究，提高框架的刚度，减轻结构重量。上述研究均进行了拓扑优化，未考虑不确定性。然而，忽略不确定性可能会导致结构的不可靠性甚至失效。

在实际的工程结构中，由于制造和各种环境因素的影响，所施加的载荷、材料参数和结构几何形状等参数不可避免地包含不确定性。由确定性拓扑设计优化得到的拓扑结构可能会违反这些约束条件，不能满足设计的性能要求。因此，有必要考虑不确定性，并使用适当的模型来判断优化结构的可靠性。Liu等[22]和Thampan等[23]最初在桁架的单目标拓扑优化中引入了可靠性作为一个约束条件。随后，许多研究人员开始考虑不确定性对可靠性的影响，提出了一种以正态分布形式表示不确定性参数的概率方法，以结构性能为目标，以失效概率为约束，进行基于可靠性的拓扑优化[24]。在Greiner等[25]的一项研究中，外荷载和屈服应力的不确定性用高斯正态分布表示，结构质量和可靠性是桁架拓扑优化的目标。Jalalpour等[26]研究了桁架的几何形状和材料的不确定性，并提出了一种随机刚度可靠性拓扑优化模型。Torii等[27]提出了一种同时优化桁架的几何形状和拓扑结构的概率方法，考虑了所施加的力和屈服应力的不确定性。此外，在基于可靠性的结构拓扑优化中，存在各种类型的不确定性。这些非概率不确定性主要用不确定但有界（区间或凸）集[28‒29]或模糊集[30]表示。不同类型的不确定性也混合成了一个可靠性问题，导致了概率-非概率混合可靠性分析方法[31‒33]和其他混合形式的提出。非概率方法和混合方法已经将解决方案扩展到不确定问题。综合考虑实际问题，在本研究中，选择了概率模型来研究随机不确定性。

根据这些过去的研究，有两个问题值得思考。首先，不确定性的可靠性分析和拓扑优化的耦合可能会导致一个低效的求解过程。其次，基于不确定参数建立的可靠性拓扑优化模型可能不适用于教与学优化（TLBO）算法。这将对算法的收敛速度和精度产生不利的影响。本研究针对上述问题，进行了一些创新。首先，在实际工程中确定了不确定参数的概率分布。在可靠性分析阶段，将故障概率转换为一个可靠性指标约束。其次，根据不确定参数将其可靠性修正为确定性参数。我们还将之前的复杂优化过程解耦为一个拓扑优化过程和一个确定性的可靠性分析过程。该解耦模型适用于对算法的解析，提高了优化效率。最后，选择TLBO算法来求解设计变量。通过采用自适应教学因子对算法进行改进，使初始搜索阶段的收敛速度加快，并在经过一定次数的迭代后使搜索更加精细化。

本文的其余部分组织如下。第2节研究了该结构的特征，并建立了一个拓扑优化模型。第3节讨论了基于可靠性的不确定性参数的模型分析。第4节详细介绍了TLBO算法的求解决过程。在第5节中提供了一个优化结果的例子，然后在第6节中得出结论。

《2、液压机支撑件板系结构优化模型》

2、液压机支撑件板系结构优化模型

本节总结了液压机支架的典型结构，并提出了最优模型。

《2.1 基结构法》

2.1 基结构法

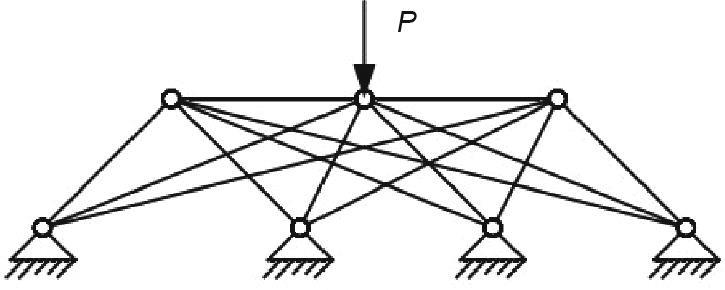
为了进行结构拓扑优化，需要将整个结构分为设计域进行研究。有两种设计域：基结构和连续结构。基结构方法是研究离散结构拓扑优化的一种常用方法，非常适合于本文的研究目标。其基本思想是在设计域中构造一组详尽的离散结构单元（桁架或梁/框架）。由桁架结构组成的基结构如图1所示。设计变量是这些单元的截面参数，如面积和厚度，以及这些单元是否存在。拓扑优化的目标是通过在设计过程中从原始的详尽单元集中删除一些单元来实现的[34]。

《图1》

图1 桁架的基结构。P：施加于桁架上的外力。

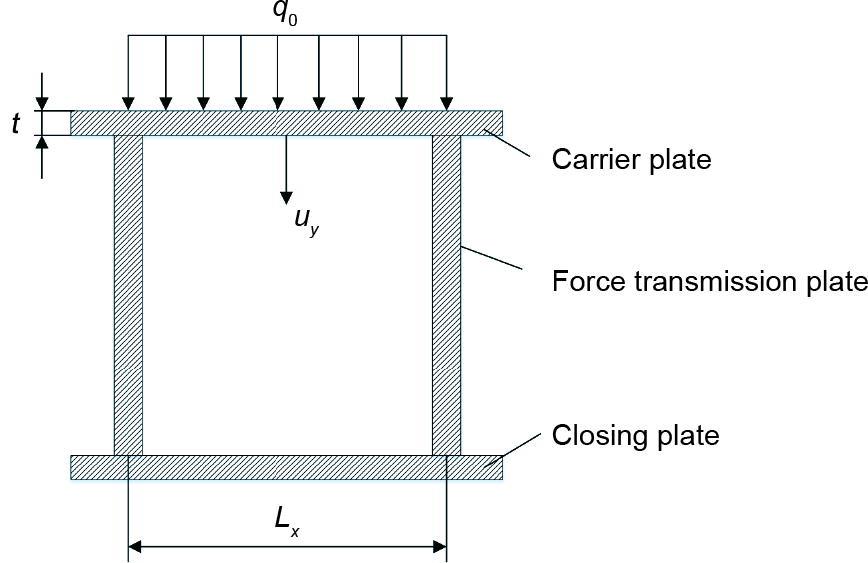
液压机支架的箱形板系结构由交错和相互连接的板单元组成。各单元之间的连接模式为刚性加固。根据不同的功能将板单元分为三个部分：承载板、传力板和封闭板。如图2所示，箱形板系结构的上部为承载板，其中施加外部载荷。中间部分的传力板垂直于传递载荷的承载板。本文讨论的拓扑优化主要针对传力板的尺寸和拓扑变量。底部是封闭板，与承载板和传力板一起封闭整体结构，从而使整体结构形成空腔结构。

《图2》

图2 板系结构的组成。L_x：传力板之间的间距。

在构造箱形板系结构的基结构时，必须将局部位移_y限制在空腔的中心。这种限制防止了基结构板的不合理间距引起的承载板的过度位移。对于给定的承载板厚度t，指定传力板的间距_x和_y。承载板中心的位移_y与外部载荷q₀有一个单调递增的关系。当外部载荷q₀增加时，位移_y变大，并且在q₀足够大时位移达到允许值[_y]。因此，板间距_x和_y（对应于[_y]）是允许的最大板间距。

《2.2 板系结构的拓扑优化模型》

2.2 板系结构的拓扑优化模型

液压机支架的板系结构为力支撑结构。其设计需要足够的刚度来满足加载要求，同时确保结构尽可能轻。因此，这是一个多目标的拓扑优化问题。在确定了液压机支架的基结构后，引入了拓扑变量 $r = [r_{1}, r_{2}, \dots, r_{n}]^{T}$ 和板的厚度变量 $t = [t_{1}, t_{2}, \dots, t_{n}]^{T}$ 。其中，n为板的数量；T为矩阵转置。拓扑变量表示该板是否存在。当将拓扑变量设置为零时，板厚度变量也设置为零。通过同时考虑这两个变量，解决了拓扑优化中拓扑变量与板厚度变量之间的耦合问题。板系结构的总重量可以表示如下：

$W = \sum_{i = 1}^{n} r_{i} A_{i} t_{i} ρ$ （1）

式中，ρ为材料密度；_i（_i∈{0,1}）是板的拓扑变量；_i是板面积；_i为板的厚度。

结构承载能力的大小可以用结构的整体应变能来表征。当载荷固定时，结构的应变能越小，结构的柔韧性就越小，结构的刚度也就越大。给定载荷和约束边界条件下的结构应变能满足以下公式：

$U = \int_{Ω}^{} σ^{T} ε d Ω = d^{T} k d$ （2）

式中，U为结构应变能；为应力矩阵；为应变矩阵；Ω为结构体积；为荷载产生的结构位移矩阵；为结构刚度矩阵。

液压机支撑件板系结构的拓扑优化需要在结构质量和承载能力两个目标函数之间达到最优的折衷方案。通常对多目标问题进行多目标优化，生成一系列的帕累托解，然后进行选择性优化。本研究将多目标拓扑优化问题转化为单目标问题。在结构拓扑优化中，范数方法常用于多目标函数的转化[35‒36]。距离函数的定义如下：

$D = {[\sum_{i} λ_{i} {(f_{i} (t) - s_{i})}^{p}]}^{1 / p}$ （3）

式中，_i表示第i个目标函数的加权因子；_i(t)为设计变量的目标函数值；t为板厚度的设计变量；_i为目标函数的初始值；p为惩罚因子。

液压机支撑件板系结构的拓扑优化设计采用了基结构方法。板的厚度是设计变量，其目标是最小化板系结构的应变能和重量。为了便于计算，将这两个目标乘以权重，然后合并成一个目标_i(t)。在拓扑优化过程中，不同的目标函数之间存在不同的数量级。如果直接取实际值作为优化目标，较小级的目标函数递减，较大级的目标函数占主导地位。因此，在多目标函数的建模过程中需要一个规范化过程。该拓扑优化问题采用了一种同时考虑横截面变量和拓扑变量的混合变量拓扑优化模型。需要求解的设计变量是拓扑变量 $r = {[r_{1}, r_{2}, \dots, r_{n}]}^{T}$ 和板的厚度变量 $t = {[t_{1}, t_{2}, \dots, t_{n}]}^{T}$ 。

$\begin{matrix} m i n f (t) = λ (\frac{W}{W_{0}}) - (1 - λ) (\frac{E_{0}}{E}) \\ s . t . σ_{j} \leq [σ] j = 1,2, \dots, m \\ u_{k} \leq [u] k = 1,2, \dots, l \\ t_{w} \in T_{w} w = 1,2, \dots, n_{1} \\ t_{v} \in T_{v} v = 1,2, \dots, n_{2} \\ n_{1} + n_{2} = n \\ r_{i} \{\begin{matrix} 1 t_{i} > 0 \\ 0 t_{i} = 0 \end{matrix} i = 1,2, \dots, n \\ r_{w} = 1 w = 1,2, \dots, n_{1} \\ r_{v} \in \{0,1\} v = 1,2, \dots, n_{2} \end{matrix}$ （4）

式中，W为结构目标权重；W₀是结构初始权重；E是结构目标应变能；E₀为结构初始应变能；λ为加权因子；[σ]为容许应力约束；[u]为允许的最大位移；_w为不允许删除的板厚度；_v是可以删除的板厚度；_w为不允许删除的板厚度集；_v为可以删除的板厚度集；_w是不能删除的拓扑变量；_v是可以删除的板拓扑变量。

在上面的拓扑优化模型[公式（4）]中，将约束分为应力约束和位移约束。应力约束将结构指定点处的应力限制为不大于材料的容许应力。位移约束是指要求结构指定位置处的位移小于规定的允许位移。结构的多目标拓扑优化得到了一系列可行解。通过判别函数对这些解进行判断，确定最优折衷解，从而得到最终结果。判别函数c表示如下：

$c = \sum_{i} {(\frac{f_{i}^{*} - f_{i} (t)}{f_{i} (t)})}^{2}$ （5）

式中，_i是第i个目标函数的理想可行解。通过计算对应不同加权因子的判别函数值，得到了相应的判别函数值极小时的最优加权因子。该加权因子下的拓扑优化结果是最终的优化结果。

《3、液压机支撑件板系结构的可靠性分析》

3、液压机支撑件板系结构的可靠性分析

将液压机支撑件板系结构的可靠性分析所涉及的参数分为确定性参数和不确定性参数。确定性参数与优化目标函数和约束一起构成了一个数学优化模型。

拓扑优化中涉及的不确定性变量包括材料力学参数、外部荷载大小和板高度。在本研究中，使用一个概率模型来描述这些变量，并研究它们的随机不确定性。将不确定性参数转化为符合一定概率分布的随机变量，如正态分布和指数分布。然后，得到了结构响应的概率分布。可靠性拓扑优化的数学模型可以描述为

$\{\begin{matrix} f i n d t, r \\ m i n f (t, r) \\ s . t . P r [G_{i} (t, r, y) \leq 0] \leq P_{f_{i}}^{T} i = 1, \dots, m \\ h_{j} (t, r) \leq 0 j = 1, \dots, n \\ t_{m i n} \leq t \leq t_{m a x} \\ y = [E, F, H] \end{matrix}$ （6）

式中，为随机变量的向量，考虑了结构材料的弹性模量E、外部荷载大小F，以及板高度H的不确定性；f ()为目标函数； $P r [G_{i} (t, r, y) \leq 0]$ 表示结构失效的概率； $P_{f_{i}}^{T}$ 为允许的失效概率；_j(, )是该结构的另一个约束条件。

可靠性拓扑优化的目的是完成结构的优化设计，保证失效概率小于允许的失效概率。在优化计算过程中，需要提供不确定参数的概率密度分布和精确的性能函数，以准确地计算失效概率。在理论上，通过对联合概率密度函数的积分计算，可以得到结构的可靠性。但在实际应用中，该函数通常是高维的，而极限状态函数是隐式的。在一般的可靠性设计过程中，通常采用近似方法使极限状态函数显式，或采用局部展开法近似失效概率计算。在利用一次二阶矩法计算可靠性指标时，将独立的随机输入变量转化为标准的正态随机变量。失效概率是用于标准正态空间而不是原始空间。将极限状态面上最接近原点的点定义为最可能故障（MPP）点。此外，在极限状态面上，距离原点的最短距离是可靠性指标β。因此，将故障概率转换为表达式的可靠性指标约束：

$P_{f_{i}} \leq P_{f_{i}}^{T} \Rightarrow β_{i} \geq β_{i}^{T}$ （7）

式中，_i结构第i个极限状态的可靠性指标， $β_{i}^{T}$ 为对应的目标可靠性指标。Φ^-1是标准正态分布的逆函数，将允许的失效概率 $P_{f_{i}}^{T}$ 转化为 $β_{i}^{T}$ 。

$β_{i}^{T} = - Φ^{- 1} (P_{f_{i}}^{T})$ （8）

传统的具有不确定性的可靠性优化设计包括拓扑优化迭代过程和可靠性分析过程。两者都相互嵌套，使得解决方案过程变得复杂。该解耦方法是求解具有高维数、小故障概率、复杂或隐式极限状态函数的基于可靠性优化问题的一种有效、可行的方法。求解故障概率函数是解耦方法的关键。失效概率函数被定义为随设计变量变化的函数，使原问题可以转化为传统的确定性优化问题。变换后的确定性优化问题可以用一般的优化算法来求解。本文采用解耦的方法，将可靠性拓扑优化过程分为可靠性分析和确定性拓扑优化两部分。一次可靠度方法中可靠性指标的几何意义如图3所示。可以找到设计点P^*对应于该随机变量的函数的可靠性指标和灵敏度信息。然后，根据灵敏度信息对不确定性参数进行修正。这使不确定性参数具有确定性，进而基于所获得的确定性参数进行确定性拓扑设计优化。

《图3》

图3 一次可靠度的几何意义。μ₁：第一个归一化的随机变量；μ₂：第二个归一化的随机变量；μ₁*：最有可能失效点的第一个标准化随机变量；μ₂*：最有可能失效点的第二个归一化随机变量。

对于给定的故障情况，结合可靠性指标的几何意义，可以使用以下针对随机变量的优化模型来求解可靠性指标β [37]：

$\begin{matrix} β = m i n μ = \sqrt[]{\sum μ_{j}^{2}} \\ s . t . β \geq β^{T} \end{matrix}$ （9）

式中，μ为归一化的随机变量。

在求解过程中，结构可靠性指标对正常随机变量的敏感性可以求解为

$\frac{\partial β}{\partial u_{i}} = \frac{1}{2} (\sum μ_{j}^{2})^{- 1 / 2} \cdot 2 μ_{j} = \frac{μ_{j}}{β (μ)}$ （10）

求解得到的最优解可以理解为对于一个给定的故障情况找到MPP μ*。利用μ将模型的随机参数修改为确定性参数μ*。修改过程表示为

$y_{i} = \{\begin{matrix} η_{y_{i}} + μ_{i} σ_{y_{i}}, i f \frac{\partial f}{\partial η_{y_{i}}} \geq 0 \\ η_{y_{i}} - μ_{i} σ_{y_{i}}, i f \frac{\partial f}{\partial η_{y_{i}}} < 0 \end{matrix}$ （11）

式中， $η_{y_{i}}$ 和 $σ_{y_{i}}$ 分别表示不确定性参数 $y_{i}$ 的均值和标准差。采用有限差分法计算上述目标函数中不确定参数的敏感性：

$\frac{\partial f}{\partial η_{y_{i}}} = \frac{∆ f}{Δ η_{y_{i}}} = \frac{f (η_{x_{i}} + Δ η_{x_{i}}) - f (η_{x_{i}})}{Δ η_{y_{i}}}$ （12）

在对不确定参数进行修正后，可以将板系结构的可靠性拓扑优化问题转化为等效的确定性拓扑优化问题。

$\{\begin{matrix} g i v e n y = [E, F, H] \\ f i n d t, r \\ m i n f (t, r) \\ s . t . G_{i} (t, r) \leq 0 i = 1, \dots, m \\ h_{j} (t, r) \leq 0 j = 1, \dots, n \\ t_{m i n} \leq t \leq t_{m a x} \end{matrix}$ （13）

采用解耦方法进行可靠性拓扑优化计算，忽略了性能函数的影响。但与启发式方法相结合，该方法有效地提高了计算效率，便于优化计算。

《4、优化解的过程》

4、优化解的过程

本研究选择的TLBO算法是一种具有收敛性和效率优势的群体智能算法。与大多数受自然启发的优化算法相比，TLBO算法没有影响算法性能的最优控制参数。对于TLBO，假设自然行为的性能总是最优的，这也降低了算法初始化的复杂性。通过大量的研究，对该算法进行了深入的探索和发展。Rao等[38]提出了TLBO算法用以模拟教学和学习过程。TLBO算法及其改进形式已应用于各种优化场景[39‒40]，包括离散结构优化。Togan [41]采用TLBO算法对平面钢架进行设计优化。Degertekin等[42]和Camp等[43]将TLBO算法分别应用于平面桁架和空间桁架的设计优化。使用采用离散设计变量的TLBO算法优化了桁架结构。

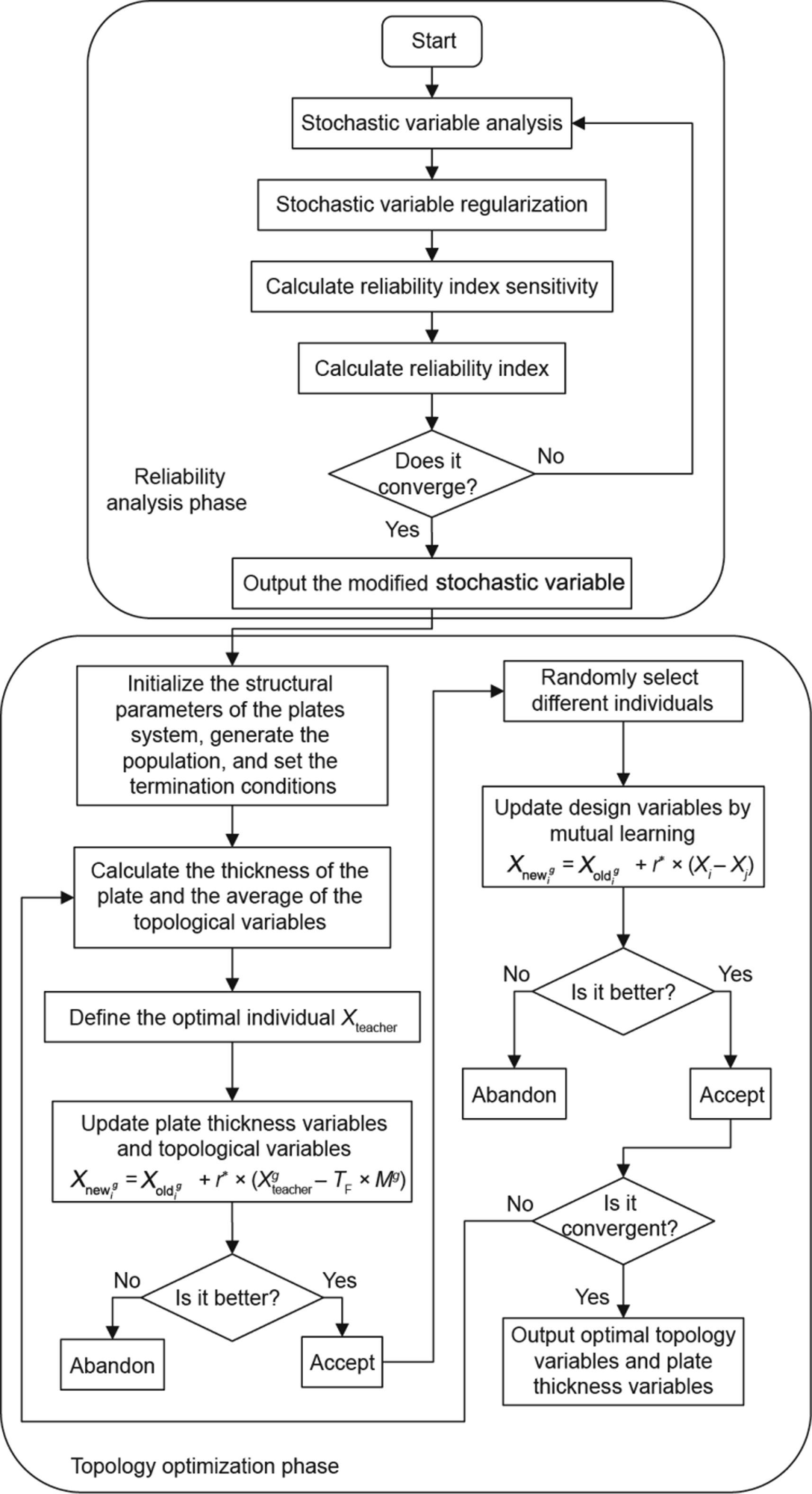
根据液压机支撑件板系结构的可靠性拓扑设计优化，基于一系列不确定性参数的优化计算，使结构更真实地反映工程实践。可靠性拓扑优化流程图如图4所示。

《图4》

图4 一种液压机支撑件板系结构的可靠性拓扑结构优化流程图。Xoldig：第i个学生在学习前的成绩；Xnewig：第i个学生在学习后的成绩；T_F：教学因子；X_i、X_j：两个成绩随机的不同的学生；M^g：单个设计变量的平均值；g是迭代的次数；r*是随机数。

通过对液压机支架的可靠性分析，并根据不确定性参数进行修正，利用TLBO算法得到了拓扑优化解，该算法分为教学和互学两个阶段。

《4.1 种群初始化》

4.1 种群初始化

N维P列的初始种群是随机生成的，其中N表示学生的数量，P是变量的数量。指定最大迭代次数G和初始条件，以及每个变量的上下限。种群生成过程如等式（14）所示，其中该值是介于0到1之间的一个随机数。

$x_{(i, j)}^{1} = x_{j}^{m i n} + r^{*} \times (x_{j}^{m a x} - x_{j}^{m i n})$ （14）

式中， $x_{(i, j)}^{1}$ 为初始个体； $x_{j}^{m a x}$ 、 $x_{j}^{m i n}$ 分别为变量的上限和下限。

《4.2 教学阶段》

4.2 教学阶段

在这一阶段，计算了初始种群中每个个体的自适应值。然后，选择最优的个体作为“教师”来教其他个体，即“学生”。当迭代次数为g时， $X_{t e a c h e r}^{g}$ 表示当前种群中的“教师”个体，以及M是个体设计变量的平均值。这个“学生”会根据等式（15）来学习和获得进步：

$X_{n e w_{i}^{g}} = X_{o l d_{i}^{g}} + r^{*} \times (X_{t e a c h e r}^{g} - T_{F} \times M^{g})$ （15）

式中， $X_{o l d_{i}^{g}}$ 和 $X_{n e w_{i}^{g}}$ 分别表示第i个学生学习前后的成绩；T_F表示教学因子，通常在1或2中随机选择。

《4.3 相互学习阶段》

4.3 相互学习阶段

每个学生在这个阶段通过相互学习来提高个体的自适应值。教学阶段结束后，随机为一个学生_i选择另一个学生_h（h ≠ i）来分析他们之间的差距并同时调整。

由于拓扑变量是板系结构拓扑优化中的一个离散值，因此在迭代学习过程中，该变量被视为[0, 1]之间的一个连续变量。在计算目标函数值和约束时，拓扑变量是经过四舍五入的，因此在最终计算中在结果被表示时，拓扑变量是经过四舍五入的。这种处理模式确保了拓扑变量在学习进化过程中保持随机性。

标准的TLBO算法不能处理工程应用中涉及的约束问题。引入惩罚函数，将有约束的问题转化为无约束的问题。惩罚函数的一般形式是

$ϕ (x) = f (x) + p (x)$ （16）

式中，φ(x)是加到惩罚项上的综合目标函数；p(x)是惩罚项，表示为

$p (x) = \sum_{i = 1}^{m} r_{i} \cdot m a x {(0, g_{i} (x))}^{2} + \sum_{j = 1}^{p} c_{j} \cdot |h_{j} (x)|$ （17）

式中，_i和_j是惩罚因素；_i(x)和_j(x)分别为不等式约束和相等式约束。

在标准TLBO算法的计算过程中，教学因子T_F的变化是至关重要的，其值会影响迭代搜索的速率和准确性。一般情况下，教学因子的值被系统随机选择为1或2。在优化迭代的计算过程中，如果T_F较小，优化过程的收敛速度就会减慢，搜索结果也会更加精细化。如果值很大，收敛速度会更快，但算法可能为时过早。Rao等[45]对T_F的值进行了讨论和改进，并对TLBO算法进行了优化。Niknam等[46]将教学因子的值与在校生的平均成绩和教师的水平联系起来。T_F用于表示在第i次迭代时，学生成绩（_i）达到教师水平（_i）的比例： $T_{F} = M_{i} / T_{i}$ 。本研究采用自适应教学因子计算方法[47]，表示为

$T_{F} = T_{F_{m i n}} + a b s (\frac{f (M_{i}) - f (M_{o p t, i})}{f (M_{i})})$ （18）

式中，M_opt,_i是通过教学和相互学习优化第i次迭代后每位学生的平均成绩。T_F $_{m i n}$ = 1；当f (_i)为0，T_F等于1。教学因子的这个值使初始搜索阶段的收敛速度更快，而更详细的搜索是经过多次迭代后达到一定次数后被使用的。

选取Griewank和Rastrigrin数值函数对原TLBO和改进算法进行比较，验证了改进算法的有效性。这两个函数都是典型的具有许多局部极小值的非线性多模态函数。通过优化算法很难找到它们的全局最小值。函数维数设为30，算法总体规模为10，最大迭代次数为100，教学因子的最大值为2，最小值为1。

原来的TLBO算法和改进的TLBO算法在经过一定次数的迭代后都能收敛到一个全局最优值。但改进后的TLBO算法在收敛速度方面比原算法有明显的优势。原来的TLBO算法直到90代以上才收敛到全局最优值，而改进的TLBO算法在不到20代内收敛。测试结果表明，改进后的算法更容易跳出局部最优值。在计算高维复杂模型的拓扑优化时，也大大提高了算法的效率。

《5、示例分析》

5、示例分析

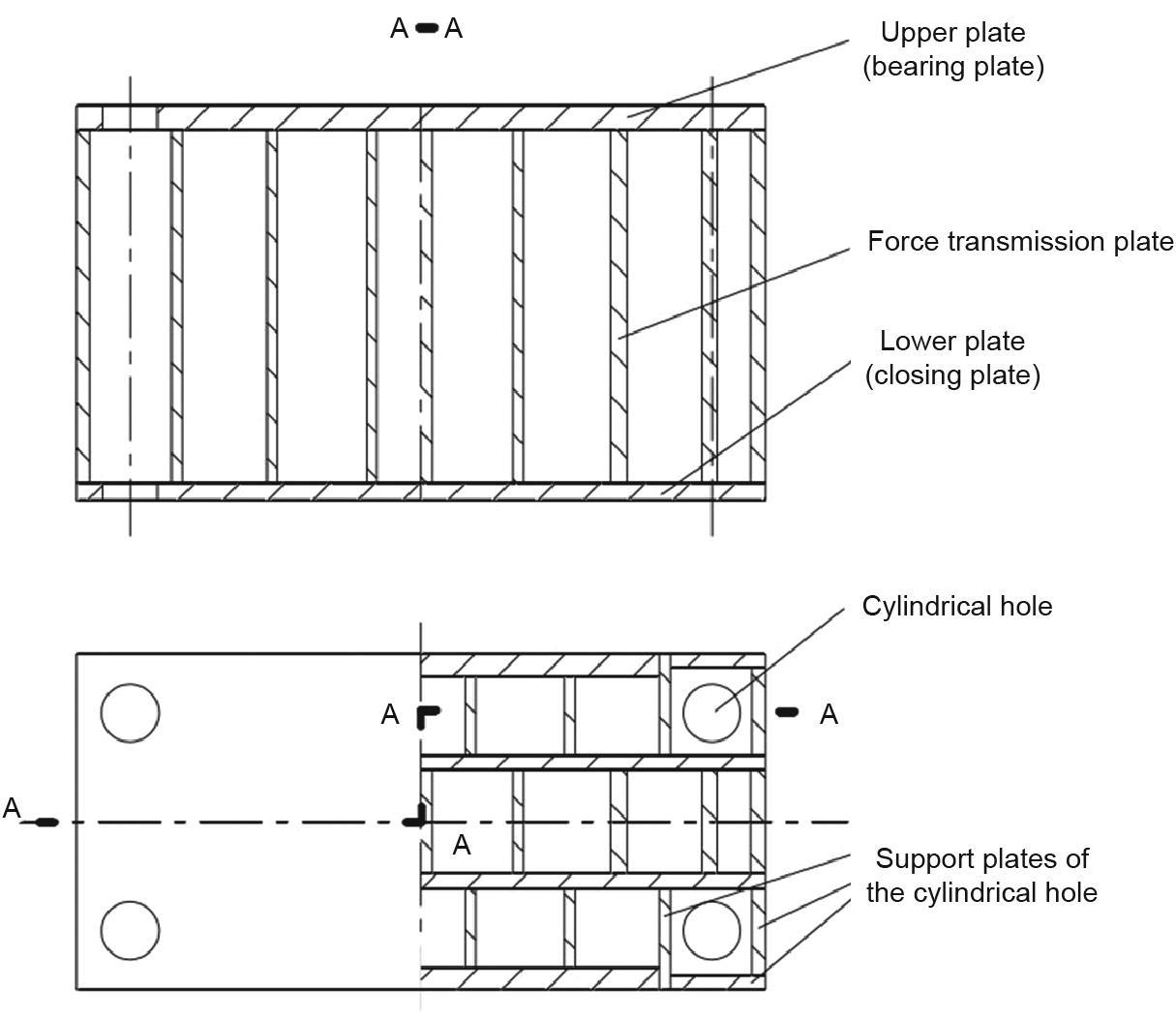
液压机支架为箱形板系结构。该结构主要由通过焊接或铸造形成的多边形板组成。内部与平板交错排列，形成一个独立的空间。上部由一个承重板支撑。由于制造工艺的不同，液压机支架的板系排布也有所不同。在拓扑优化中，针对不同的工艺形式，基结构需要采用不同的施工方式，以反映板系排布和工艺特点。图5中显示了两种典型的排布形式：整齐方格和错位方格。下面，将介绍对整齐方格和错位方格布局的拓扑优化。这两个优化目标都包括板系结构的总质量和载荷刚度，而局部最大位移被设置为满足可靠性要求的约束条件。

《图5》

图5 焊接板结构。

结构设计参数见表1。目标性能是由结构的整体应变能来定义的。结构质量被限制为结构原始质量的80%。迭代的次数被设置为100次。每个板的上限厚度设置为5 cm，承载板在z方向上的最大位移设置为2.5 mm。边界条件采用了底板圆柱孔周围的完全约束，在顶板中心的1.8 m × 1.2 m矩形区域内施加载荷，并采用了位移约束。荷载、材料弹性模量和板高度均设为正态随机变量。结构的不确定性参数如表2所示。在设置参数后，采用解耦方法对随机变量的灵敏度进行计算和修正。然后，将修正后的随机变量代替成数学拓扑优化模型进行计算。

《表1》

表1 结构设计参数值

Parameter	Value
Overall length (m)	2.50
Overall width (m)	1.50
Material density (kg∙m^-3)	0.48
Poisson ratio	0.33
Plate thickness range (m)	0‒0.05
Displacement constrains (mm)	0.50

《表2》

表2 修改前不确定参数值

Types	Load size (MPa)	Elastic modulus (× 10¹¹ Pa)	Plate height (m)
Average value	0.76	2.1	0.48
Standard deviation value	0.20	0.1	0.05

底座四角处的圆柱孔的支撑板因其功能而设置为不可移动板，而其他支撑板可以被添加或删除。拓扑优化目标可靠性β^T设为3，根据优化迭代结果和判别函数[式（5）]，选择理想权重因子λ为0.8。承载板的布局是对称的，因此只需要对左下角进行建模分析，而其余部分则采用对称的方法计算。在本例中，各部分的材料是相同的，因此，只有结构体积被作为目标函数进行计算。各板的优化拓扑变量和板厚度变量分别列于表3和表4。最终的拓扑优化结果如表5所示。整齐方格结构和错位方格结构及其数量分别如图6和图7所示。拓扑优化的迭代过程和最终的优化结果如图8至图11所示。

《表3》

表3 最优整齐方格板系结构的拓扑结构和尺寸变量

Number	Deterministic topology optimization		Reliability topology optimization
Number	Topology variables	Size variables	Topology variables	Size variables
X11	1	0.010	1	0.012
X12	1	0.017	1	0.019
X13	0	0	0	0
X21	1	0.013	1	0.015
X22	1	0.050	1	0.050
X23	1	0.042	1	0.049
Y11	1	0.034	1	0.010
Y12	1	0.038	1	0.050
Y13	0	0	1	0.010
Y21	0	0	1	0.025
Y22	1	0.026	0	0
Y23	0	0	0	0

《表4》

表4 最优错位方格板系结构的拓扑结构和尺寸变量

Number	Deterministic topology optimization		Reliability topology optimization
Number	Topology variables	Size variables	Topology variables	Size variables
X11	1	0.012	1	0.017
X12	1	0.014	1	0.032
X13	0	0	0	0
X21	1	0.013	1	0.020
X22	1	0.047	1	0.050
X23	1	0.039	1	0.030
Y11	1	0.010	1	0.028
Y12	0	0	1	0.020
Y13	0	0	0	0
Y21	0	0	0	0
Y22	0	0	0	0
Y23	0	0	1	0.039

《表5》

表5 拓扑优化结果的比较

Types	Weight ratio (W/W₀)		Strain energy ratio (E/E₀)		Maximum displacement (mm)
Types	Certainty	Reliability	Certainty	Reliability	Certainty	Reliability
Neat grid	0.76	0.77	1.44	1.35	0.48	0.49
Staggered grid	0.71	0.78	1.56	1.32	0.45	0.47

《图6》

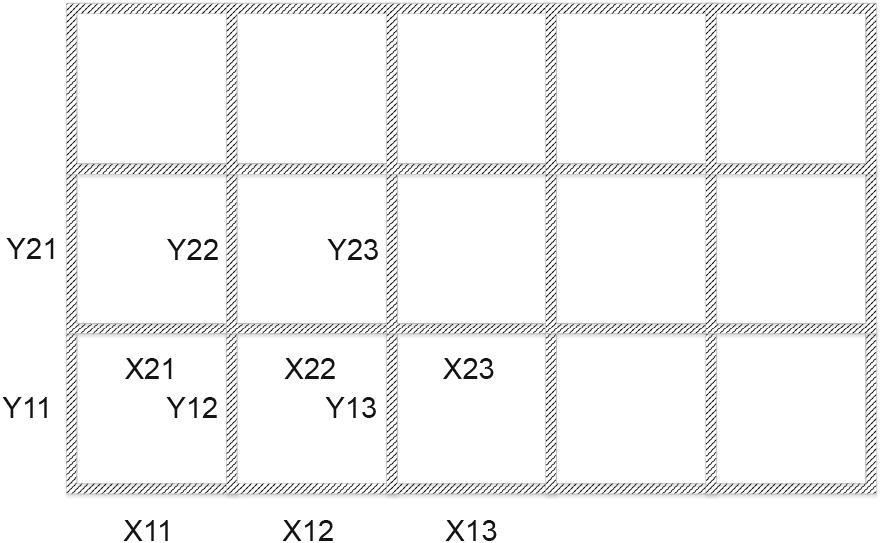
图6 整齐方格基结构。

《图7》

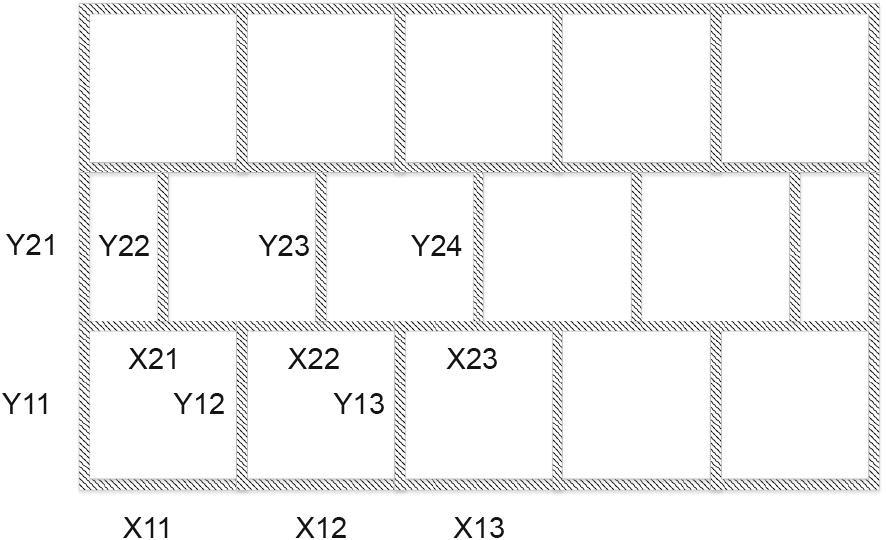
图7 错位方格基结构。

《图8》

图8 整齐方格基结构的拓扑优化。（a）确定性拓扑优化结果；（b）可靠性拓扑优化结果（β^T = 3）。

《图9》

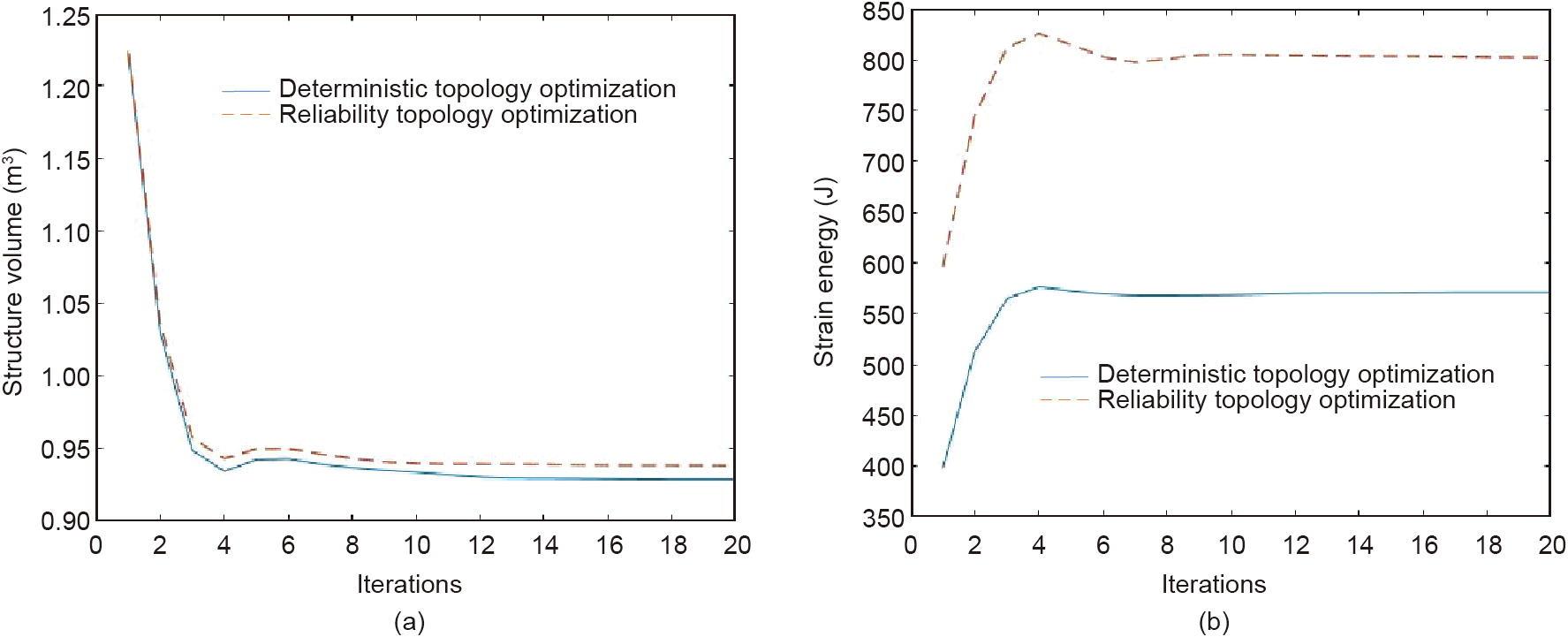
图9 整齐方格基结构目标函数的收敛过程。（a）体积收敛过程；（b）应变能收敛过程。

《图10》

图10 错位方格基结构的拓扑结构优化。（a）确定性拓扑优化结果；（b）可靠性拓扑优化结果（β^T= 3）。

《图11》

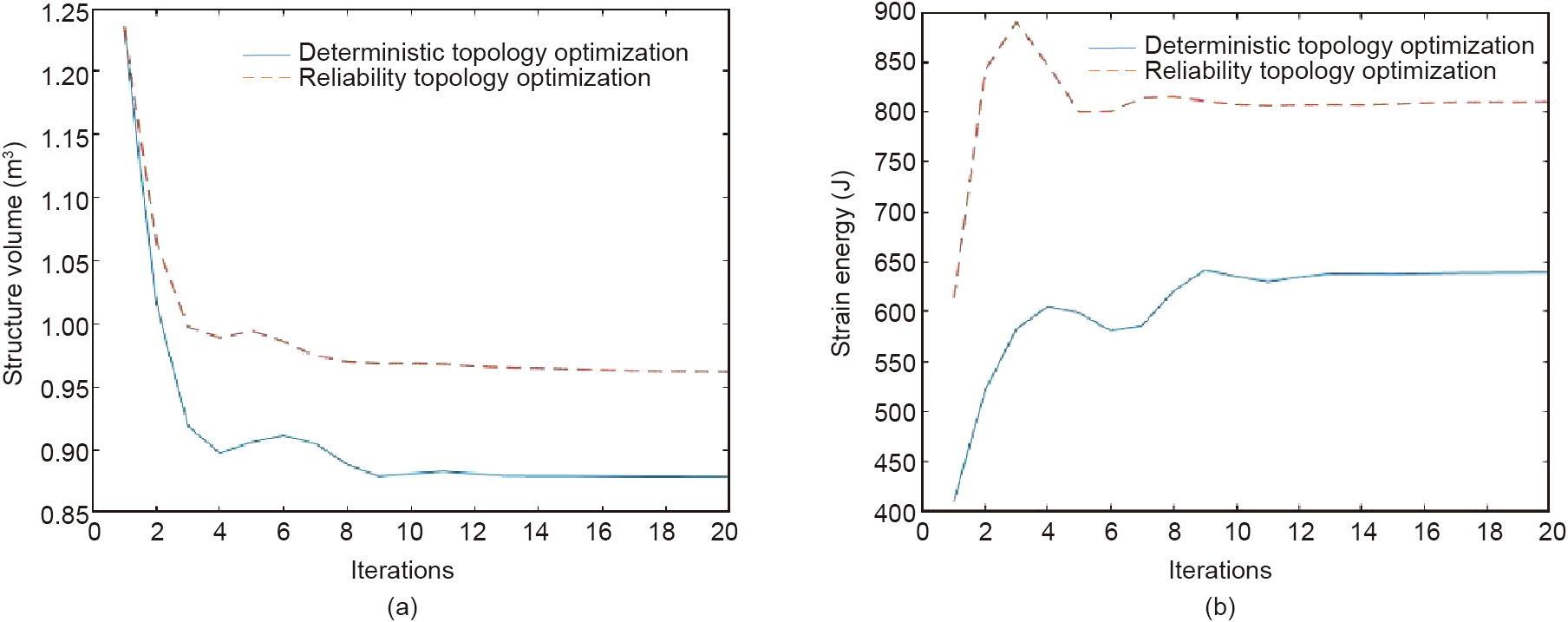
图11 错位方格结构的目标函数的收敛过程。（a）体积收敛过程；（b）应变能收敛过程。

整齐方格和错位方格结构优化后的拓扑结构和板单元分布分别如图8和图10所示。与两种基结构的拓扑优化结果相比，可靠性优化获得的结果比确定性优化获得的结果具有更多的板系结构。表3和表4显示了通过可靠性和确定性拓扑优化得到的拓扑和板厚度变量的定量数据。在整齐方格结构中，靠近底座中心的第X23号和第Y12号板的板厚度显著增加。此外，经过可靠性拓扑优化后，板Y13和板Y21的拓扑变量均为1。同样，在错位方格结构下，板厚度变量也显著增加。经过可靠性拓扑优化后，靠近结构中心的板Y12和板Y23的拓扑变量变为1。增加了结构的总材料量，提高了结构的可靠性。

体积和应变能目标函数的迭代变化分别如图9和11所示（分别基于不同的基结构）。对于两种基结构中的体积目标函数，可靠性拓扑优化的最终收敛值都大于确定性拓扑优化的最终收敛值。这一结果与图8和图10中显示的直观结果一致。对于应变能目标函数，应变能越高，支撑刚度就越小。通过可靠性拓扑优化计算的结构应变能高于确定性拓扑优化。这表明，在对随机参数进行修正后，结构满足优化约束，支撑刚度较小。结果表明，该结构获得了更强的抗失效能力和更高的可靠性。

表5给出了两种基结构的确定性和可靠性拓扑优化结果。优化结果满足0.5 mm的位移约束。然而，使用两种不同的基结构得到的结果略有不同。整齐方格结构的可靠性拓扑优化在权重比上增加较小，仅从0.76增加到0.77。在错位方格结构中，权重比从0.71增加到0.78。在这两种情况下，使用可靠性拓扑优化过程，最终优化结果的总应变能与初始结构的比值都显著降低。整齐方格的应变能与原始应变能的比值为1.35，错位方格的应变能与原始应变能的比值为1.32。当结构较轻时，可靠性拓扑优化降低了结构支撑刚度。因此，可以构造该结构以满足预定的可靠性指标。

与确定性拓扑优化相比，可靠性拓扑优化得到的结果更加保守、权重较大、应变能小，不确定条件下结构的整体刚度较大。但与未优化的结构相比，确定性拓扑优化的权重值和可靠性拓扑优化的权重值减少，而应变能增加。同时，在不确定条件下，基于可靠性拓扑优化的结构满足可靠性要求，故障风险较小。数值实例表明，可靠性拓扑优化在平衡结构性能和环境保护方面是有效的。

《6、结论》

6、结论

对液压机结构进行轻量化设计，在保证高可靠性的基础上节约资源。本文以降低液压机支架质量为目的，研究了具有众多的不确定性的离散拓扑优化方法。首先，采用基结构方法将液压机的支架分成一个板系结构，同时改变板单元的数量并优化它们的尺寸。其次，通过概率分布，将载荷、尺寸参数和材料参数的不确定性转化为随机变量。根据可靠性指标，简化了参数的可靠性和不确定性的失效函数。解耦方法将二次嵌套的可靠性计算和拓扑优化过程划分为两个独立的部分。最后，采用TLBO算法求解解耦模型，参数少、结果简单、求解速度快。通过添加一个自适应教学因子来改进TLBO算法，以便在初始阶段收敛得更快，同时在后期阶段实现更精细的搜索。采用该方法对实际液压机进行了设计优化，确定了其布局和尺寸方面的优化设计方案。在本设计中，支撑结构的材料被充分利用，以实现整体结构的轻质化，确保结构设计在经济性和安全性之间的平衡。

然而，本研究也存在一定的局限性。在某些情况下，不确定参数只能由一个简单的范围来确定，而这是本研究中概率模型所无法处理的。此外，解耦方法忽略了不确定参数性能函数的影响，提高了计算效率。基于可靠性的拓扑优化只在很小程度上降低了能源和材料成本。换句话说，该方法主要提高了各材料单元的利用率。未来的研究需要关注这些问题，以找到更合适的方法，提出一个模型来处理以不同形式表示的不确定性，并试图不断提高模型描述不确定性的准确性。未来的研究可能会探索和应用一种比解耦方法更有效的算法来解决可靠性拓扑优化问题。另外，还可以将拓扑优化与其他优化方法相结合，以实现更大程度的轻量化和资源节约。

展示更多