Computational Design of Rare-Earth Reduced Permanent Magnets

Abstract

Multiscale simulation is a key research tool in the quest for new permanent magnets. Starting with first principles methods, a sequence of simulation methods can be applied to calculate the maximum possible coercive field and expected energy density product of a magnet made from a novel magnetic material composition. Iron (Fe)-rich magnetic phases suitable for permanent magnets can be found by means of adaptive genetic algorithms. The intrinsic properties computed by ab initio simulations are used as input for micromagnetic simulations of the hysteresis properties of permanent magnets with a realistic structure. Using machine learning techniques, the magnet’s structure can be optimized so that the upper limits for coercivity and energy density product for a given phase can be estimated. Structure property relations of synthetic permanent magnets were computed for several candidate hard magnetic phases. The following pairs (coercive field (T), energy density product (kJ·m⁻³)) were obtained for iron-tin-antimony (Fe₃Sn_0.75Sb_0.25): (0.49, 290), L1₀-ordered iron-nickel (L1₀ FeNi): (1, 400), cobalt-iron-tantalum (CoFe₆Ta): (0.87, 425), and manganese-aluminum (MnAl): (0.53, 80).

Content

《1. Introduction》

1. Introduction

Permanent magnets are widely used in modern society. Important markets for permanent magnets [1] are wind power, hybrid and electric vehicles, electric bikes, air conditioning, acoustic transducers, and hard disk drives. With the growing demand for permanent magnets in environmentally friendly transport and power generation [2], there is an ongoing quest to reduce the rare-earth content or use alternative rare-earth-efficient or rare-earth-free hard magnetic phases. Some of the considered hard magnetic phases may bridge the gap between ferrites and highperformance Nd₂Fe₁₄B-based magnets [3].

In this work, we present an overview of how the magnetic properties of a virtual magnet can be predicted, starting from first principles. The materials modeling workflow in this paper is an example for traditional multiscale simulations with parameter passing. Several physical models are linked together in order to compute the hysteresis properties of permanent magnets: Genetic algorithms in combination with density functional theory guide the search for stable uniaxial ferromagnetic phases. This process may be assisted by mining materials databases. Density functional theory is then applied, in order to compute intrinsic magnetic properties such as spontaneous magnetization, magnetocrystalline anisotropy energy, and exchange integrals. The results feed into atomistic spin dynamics models for the computation of the magnetization, anisotropy constant, and exchange constant as a function of temperature. These temperature-dependent properties are then used as input for micromagnetic simulations. Numerical optimization tools help to tune the microstructure such that the coercive field or energy density product is maximized for a given set of intrinsic magnetic properties.

In addition, we computed the reduction of coercivity owing to thermal fluctuations [4]. Analyzing the results of the micromagnetic simulations, we can identify how much different effects such as misorientation, demagnetizing fields, and thermal fluctuations reduce the coercive field with respect to the anisotropy field of the material.

The main focus of this paper is to predict the potential for various rare-earth-free or rare-earth-reduced permanent magnetic phases with respect to expected extrinsic magnetic properties such as coercivity and energy density product. A sufficiently high coercive field and sufficiently high energy density product are the key for the application of a new phase. These properties result from the interplay between the intrinsic magnetic properties of the magnet, the magnet’s microstructure, and thermal fluctuations. Therefore, the main part of this paper covers micromagnetic results for the hysteresis properties, which will be presented for well-known magnetic phases (L1₀ FeNi, Nd_0.2Zr_0.8Fe₁₀Si₂, Sm_0.7Zr_0.3Fe₁₀Si₂) as well as for phases predicted by genetic algorithms and density functional theory (Fe₅Ge, CoFe₆Ta). For some of the phases, the intrinsic magnetic properties were computed by first principle simulations (Fe₅Ge, CoFe₆Ta, Fe₃Sn_0.75Sb_0.25) and atomistic spin dynamics (MnAl).

The results presented in this paper are centered on the micromagnetic computation of the expected performance of various hard magnetic phases. For details on the adaptive genetic algorithms (AGAs) used for the search for new magnetic phases, we refer the reader to recent articles applying this method to Fe₃Sn [5], CoFe₂P [6], and magnetic phases in the L1₀ structure [7]. First principle simulations of magnetic properties are reviewed in Ref. [8]. An overview of essential micromagnetic techniques to compute the influence of microstructure on the coercivity and energy density product is provided by Fischbacher et al. [9].

《2. Methods》

2. Methods

An AGA [7] in combination with the Vienna ab initio simulation package (VASP) [10] was used to scan the phase space for iron (Fe)- rich compounds that are non-cubic and stable. The magnetic properties were calculated with the help of the full-potential linear muffin-tin orbital method implemented in the relativistic spin polarized toolkit (RSPt) [8]. Synthetic microstructures were constructed with the open-source three-dimensional (3D) polycrystal generator tool Neper [11].

A Python script controlling the open-source computer-aided design (CAD) software Salome [12] introduces the grain boundary phase with a specific thickness and produces the finite element mesh. For these synthetic microstructures, the demagnetization curve is computed through minimization of the micromagnetic energy with a preconditioned nonlinear conjugate gradient method [13]. The search for higher coercive fields, 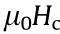, and energy density products, (BH )_max, is managed via the opensource optimization framework Dakota [14]. Thus, the optimal structure for a given hard magnetic phase can be found. To characterize the magnet, we use the M(H_ext)-loop, which gives the magnetization as a function of the external field. The demagnetization curve is then corrected by the demagnetizing field of the sample. A similar procedure is done in experiments when the hysteresis curves are not measured in a closed circuit. We then transform the magnetization to the magnetic induction, B, in order to obtain the B(H_int)-loop and the energy density product. Here, H_int is the internal field.

Finally, we consider the reduction of coercivity by thermal activation. We compute the critical value of the external field that reduces the energy barrier for nucleation to 25 k_BT, where k_B is the Boltzmann constant and T is the measurement temperature. The system is assumed to overcome this energy barrier within a waiting time of 1 s owing to thermal fluctuations [15]. We use a modified string method [16] to compute the energy barriers for different values of the external field for T = 300 K. Computation of the reduction of the coercive field through thermal activation gives the limits of the coercive field [4] of a certain hard magnetic phase.

《3. Results》

3. Results

《3.1. Rare-earth-free phases》

3.1. Rare-earth-free phases

Using an AGA [7], the crystal phase space of iron–cobalt–tanta lum (Fe–Co–Ta) was searched for non-cubic systems with high stability. For CoFe₆Ta, we performed two simulations starting from scratch with eight and 16 atoms per cell, respectively. Various non-cubic stable phases were identified. Some of the most stable non-cubic phases were tetragonal (space group 115), rhombohedral (space group 160), orthorhombic (space group 38), and orthorhombic (space group 63, where the and b lattice parameters are very similar), which had an enthalpy of formation of -0.07033, -0.06353, -0.06025, and -0.05929 eV per atom, respectively. Data and calculation details of these theoretical phases can be found in the Novamag database [17], and through Refs. [18–21]. The lowest ground-state energy was found for a monoclinic system (space group 8) with an enthalpy of formation of -0.07488 eV per atom [22]. These results correspond to highthroughput density functional theory calculations (at zerotemperature) using an AGA, where similar default settings were used for all of them with the generalized gradient approximation (GGA). To analyze the stability of these phases in more detail, it is recommended to compute the free energy at a finite temperature including the electronic, phononic, and magnetic terms [23]. In space groups 63 and 160, CoFe₆Ta shows a uniaxial magnetocrystalline anisotropy. The complete theoretical study of these phases is in progress and is planned to be reported in the near future, so here we just select and mention some preliminary results. Using the RSPt code [8], we calculated the anisotropy constant (K ) and the spontaneous magnetization () for CoFe6Ta in space group 63 to be K = 1 MJ·m^-3 and = 1.82 T, respectively.

Fig. 1 shows the micromagnetically computed B(H_int) loop for different nanostructures made of CoFe₆Ta. The grains have approximately the same volume of 34 nm × 34 nm × 146 nm, 56 nm × 56 nm × 56 nm, and 72 nm × 72 nm × 34 nm for the columns, equiaxed polyhedra, and platelets, respectively. The macroscopic shape of the magnet is cubical with an edge length of 300 nm. The volume fraction of a non-magnetic grain boundary phase is 18%, and the energy density product is 425 kJ·m^-3 .

《Fig. 1》

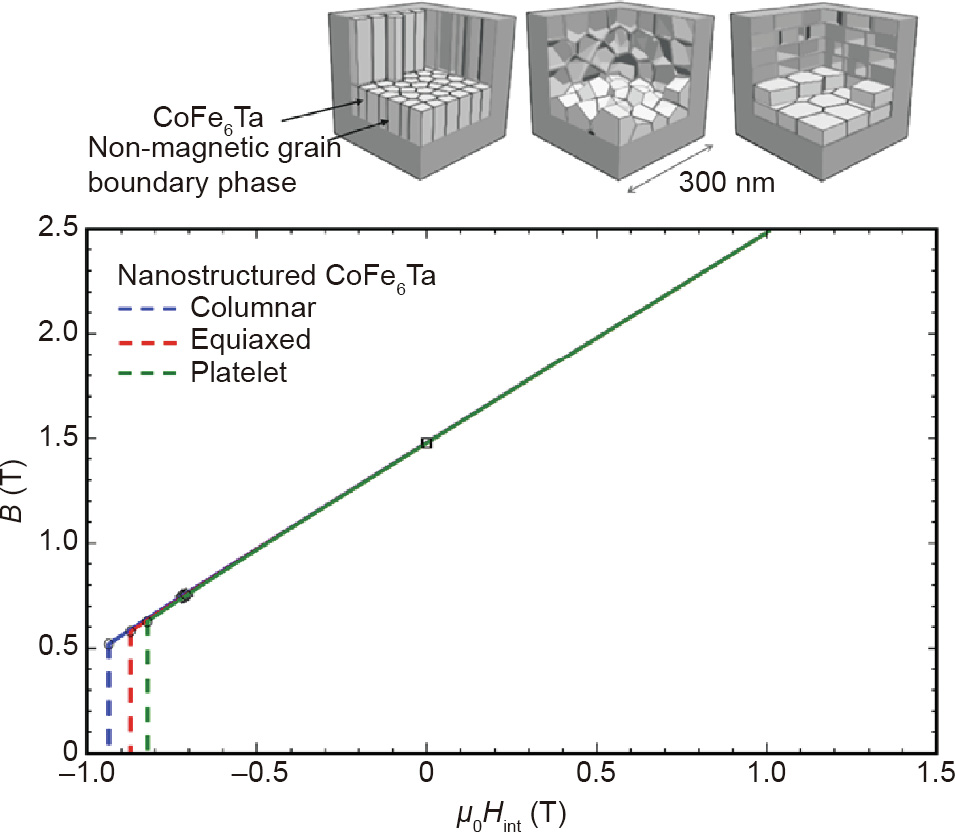
Fig. 1. Magnetic induction as a function of the internal field for nanostructured CoFe₆Ta. Nanostructuring is essential to obtain a high coercive field. The coercive field increases with an increasing aspect ratio of the grains. The aspect ratios of the columnar, equiaxed, and platelet-shaped grains are 4.3, 1, and 0.47, respectively.

Fe-rich materials with non-cubic uniaxial crystal structures are promising candidates for rare-earth-free permanent magnets. Because of their hexagonal crystal structure and high spontaneous magnetization, Fe₃Sn-based compounds were considered. However, Fe₃Sn shows an easy-plane anisotropy [24] in both simulations and experiment. Substituting tin (Sn) by antimony (Sb) changes the easy-plane anisotropy to uniaxial anisotropy. The results show a uniaxial anisotropy constant of K = 0.33 MJ·m^-3 and a spontaneous magnetization of = 1.52 T for Fe₃Sn_0.75Sb_0.25 [25]. These properties were assigned to the grains of a synthetically generated structure, where the average grain size was 50 nm. An exchange stiffness constant of A = 10 pJ·m^-1 was used. The grains were separated by a weakly ferromagnetic grain boundary (gb) phase with a magnetization of ,gb = 0.81 T and an exchange stiffness constant of Agb = 3.7 pJ·m^-1 . The micromagnetic simulation of the reversal process (Fig. 2 [25]) shows that the multi-domain states remain stable after irreversible switching due to domain wall pinning at the grain boundaries. The computed energy density product is coercivity limited. Its maximum value of 290 kJ·m^-3 may only be achieved for nanostructured systems with a grain size smaller than 50 nm. Unfortunately, Fe₃Sn_0.75Sb_0.25is not stable. Attempts to stabilize the phase by small additions of manganese (Mn) were successful. However, due to the change of the electronic structure and the number of valence electrons, the anisotropy flipped back to in-plane again [25].

《Fig. 2》

Fig. 2. Domain wall-microstructure interaction in an Fe₃Sn_0.75Sb_0.25 magnet. (a) Grain structure; (b) at an internal field of μ₀H_int = 0.49 T, the flower-like magnetic state ① breaks into a two-domain state ② with a domain wall pinned at the grain boundaries. Reproduced from Ref. [25] with permission of American Physical Society, ©2019.

《3.2. Microstructure optimization》

3.2. Microstructure optimization

To compute the influence of the microstructure on the hysteresis properties, we varied the grain size, grain shape, thickness of the grain boundary phase, and magnetization in the grain boundary phase. The design space was sampled with the help of the software tool Dakota [14].

In order to obtain a general trend for how microstructural features influence the coercive field, we used dimensionless units. The coercive field is given in the units of the anisotropy field, 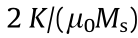. The grain boundary magnetization is measured in the units of the magnetization of the main hard magnetic phase, Ms, bulk. Grain size and grain boundary thickness are measured in the units of the Bloch parameter, , which is the characteristic length in hard magnetic materials. The results presented in Figs. 3 and 4 were obtained by varying the microstructure for magnets made of L1₀ FeNi (bulk), MnAl, and Nd_0.2Zr_0.8Fe₁₀Si₂ (Table 1) [25–30]. The granular structure used for the simulations is shown in Fig. 3(c). Because we used dimensionless units, the influence of the grain boundary phase, grain size, and grain aspect ratio on the coercivity for other hard magnetic phases can be derived from the presented data.

Fig. 3. (a) Coercive field and (b) energy density product as a function of grain boundary properties; (c) grain structure used for simulation.

Fig. 4. Influence of grain size and grain shape. The contours give the coercive field as a function of grain size and aspect ratio. The different panels refer to different saturation magnetization of the grain boundary phase with a thickness of .

The design space for the analysis of the influence of grain boundary properties on the coercivity and energy density product was spanned by the grain boundary thickness and the magnetization of the grain boundary. We varied the thickness of the grain boundary from 1.1 to 4.4, while keeping the size of the magnet constant. The magnetization of the grain boundary phase was varied from 0.05 M_s,bulk to 0.55 M_s,bulk. The exchange stiffness constant of the grain boundary phase is assumed to be proportional to its magnetization squared [31], according to 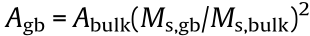. Thus, the grain boundary phase changes from almost nonmagnetic to ferromagnetic. The polycrystalline structure used for the simulations is shown in Fig. 3. The average grain size is 37.

Clearly, the maximum coercive field is reached for a thin, almost non-magnetic grain boundary phase. Both increasing the grain boundary thickness and increasing the grain boundary magnetization reduces the coercive field. The magnetization of the grain boundary phase contributes to the total magnetization. Therefore, the maximum energy density product occurs for thin grain boundaries and a moderately high magnetization in the grain boundary. We can conclude that excellent hysteresis properties can be achieved even for a ferromagnetic grain boundary, provided that its thickness is sufficiently small. For example, a coercive field of 0.4 × 2K/() is reached for a grain boundary thickness of 2, when the magnetization in the grain boundary phase is about half of its bulk value.

The weakly soft magnetic grain boundary phase acts as a soft magnetic defect. Detailed micromagnetic studies show that at such grain boundaries, magnetization reversal is initiated [32]. We see that the coercive field decreases with increasing spontaneous magnetization of the grain boundary phase. Furthermore, the coercive field decreases with increasing thickness of the grain boundary phase. Although the structure is more complicated for polycrystalline magnets with a weakly soft magnetic grain boundary phase, the effect is similar to that reported by Richter [33], who showed a similar dependence of the nucleation field on the size of a soft defect in a one-dimensional micromagnetic model. The energy to form the domain wall of the reversed nucleus increases with the decreasing thickness of the soft magnetic defect. In magnets with a thin grain boundary phase, the domain wall of the nucleus extends into the main hard magnetic phase, and the domain wall energy increases. Therefore, magnets with a thinner grain boundary phase show a higher coercive field.

Next, we modified the design space. We kept the grain boundary thickness at and varied the magnetization in the grain boundary phase, the size of the grains, and the aspect ratio of the grains. An aspect ratio greater than 1 refers to elongated, needlelike grains; an aspect ratio smaller than 1 refers to platelet-like grains.

The panels of Fig. 4 show the coercive field as a function of the grain size and the aspect ratio for different magnetizations in the grain boundary phase. For an almost non-magnetic grain boundary phase, the coercive field increases with an increasing aspect ratio. This means that magnets with needle-like grains show a higher coercive field than magnets with platelet-like grains. This effect diminishes when the magnetization of the grain boundary phase is increased. For M_s,gb = 0.4M_s,bulk, there is hardly any change of the coercive field with the aspect ratio. For large magnetization in the grain boundary phase, the trend is reversed and plateletshaped grains show a slightly higher coercive field than needlelike grains. The grain size effect on coercivity is more pronounced in platelet-shaped grains.

The results in Fig. 3 also show that the highest coercive field can be achieved for an almost non-magnetic grain boundary (0.05M_s,bulk). The coercive field is a factor of 4.5 higher than for a grain boundary phase with a spontaneous magnetization of 0.55M_s,bulk. Fig. 4 shows that the coercivity increases with decreasing grain size. We can conclude that magnets with small, exchange-decoupled grains show the highest coercive field. Indeed, the highest coercive field is found for the top left point on the top left subplot for Fig. 4 with M_s,gb = 0.02M_s,bulk: Here, we have a nanostructured system with exchange isolated grains with a grain size smaller than 20.

《3.3. Coercivity limits》

3.3. Coercivity limits

Using numerical micromagnetics, we can separate the effects that lead to a reduction of coercivity with respect to the anisotropy field of the magnet. We compute the demagnetization curve but switch off the magnetostatic field. When the computed coercive field is less than the anisotropy field, the reduction must be attributed to misalignment of the grains or secondary soft magnetic phases. In a second step, we switch on magnetostatic interactions and simulate the demagnetization curve again. The resulting decrease of the coercive field must be attributed to demagnetizing effects. Finally, we can simulate how the system escapes from a metastable state over the lowest energy barrier. This gives the temperature-dependent coercive field [4].

In the following analysis, we did not assume any soft magnetic secondary phases. The external field was oriented one degree off the easy axes of a small cube with an edge length of 40 nm. The computed effects that reduce the anisotropy fields are ① misorientation, ② demagnetizing effects, and ③ thermal fluctuations. Here, the coercive field was computed for an ideal structure: The grain size is very small (40 nm) and there are no defects. Thus, the computed coercive field is an upper limit for the coercivity for a given hard magnetic phase.

We applied this procedure to several candidate phases for rare-earth-free or rare-earth-reduced magnets. For each phase, we show the anisotropy field, the reduction owing to misorientation, the reduction by demagnetizing effects, and the reduction by thermal fluctuations (Fig. 5). The intrinsic magnetic properties used for the simulations are listed in Table 1. The anisotropy constant, spontaneous magnetization, and exchange constant for MnAl were obtained from the atomistic spin dynamics at a temperature of 300 K. Fe₅Ge is an Fe-rich binary phase predicted by an AGA. The anisotropy constant and spontaneous magnetization for Fe₅Ge, Fe₃Sn_0.75Sb_0.25, and CoFe₆Ta were obtained from first principle simulations at the temperature of 0 K. The exchange constant for Fe₅Ge and CoFe₆Ta was taken to be proportional to the spontaneous magnetization squared (A = ), where c was taken from Ms and A of a-Fe. The intrinsic material parameters for L1₀ FeNi, (Nd_0.2Zr_0.8)Fe₁₀Si₂, and (Sm_0.7Zr_0.3)Fe₁₀Si₂are experimental data for the temperature of 300 K that were taken from the literature. If no other source for the value of the exchange constant was available, we used A = 10 pJ·m^-1 [34].

The results clearly show that we cannot expect a coercive field greater than 1 T in most rare-earth-free magnets. For FeNi (bulk), a high degree of uniform chemical order was assumed. Experimentally synthesized L1₀ FeNi particles may contain patches in which the chemical order is reduced locally. The corresponding local reduction of magnetocrystalline anisotropy will deteriorate the coercivity. Similarly, crystal defects such as twins or antiphase boundaries reduce the coercive field in MnAl magnets [35]. Rare-earth magnets with the ThMn₁₂ structure with zirconium (Zr) substitution have a low rare-earth content. Moreover, the magnetocrystalline anisotropy—especially that of the (Sm,Zr)Fe₁₀- Si₂ magnet—is sufficiently high to support a reasonable coercive field. For (Nd_0.2Zr_0.8)Fe₁₀Si₂, and (Sm_0.7Zr_0.3)Fe₁₀Si₂, the coercive field computed with thermal activation (dots in Fig. 5) is 70% of the anisotropy field.

《Table 1》

Table 1 Anisotropy constant (K ), spontaneous magnetization (, and exchange constant (A ) used for the simulations presented in Fig. 5.

《Fig. 5.》

Fig. 5. Limits of coercivity. Effects that reduce the coercive field in permanent magnets for different candidate phases. The symbols give the coercive field. Star symbol: anisotropy field; X symbol: micromagnetics without magnetostatics; plus symbol: full micromagnetics; circle symbol: micromagnetics with thermal activation. Please note the different scale for the μ₀H axis for (Sm,Zr)Fe₁₀Si₂.

《4. Conclusions》

4. Conclusions

In this work, we showed how to exploit materials simulations for the computational design of next-generation rare-earthreduced permanent magnets. Based on the results presented above, we can draw the following conclusions.

(1) Nanostructuring is essential to achieve a high coercive field in rare-earth-free compounds with moderate magnetocrystalline anisotropy.

(2) Coercivity decreases with increasing magnetization in the grain boundary phase and with increasing thickness of the grain boundary phase.

(3) However, excellent permanent magnetic properties can be achieved even for moderately ferromagnetic grain boundary phases provided that the grain boundary is thin enough.

(4) The shape of the grains is only important for nearly nonmagnetic grain boundaries. For systems in which ferromagnetic Fe-containing grain boundaries are expected, the grain shape plays a minor role.

(5) Thermal fluctuations may considerably reduce the coercive field. Thus, even in perfect structures, the coercive field is well below the anisotropy field.

《Acknowledgements》

Acknowledgements

This work was supported by the EU H2020 project NOVAMAG (686056) and the Austrian Science Fund FWF (I3288-N36). Sergiu Arapan and Pablo Nieves acknowledge the European Regional Development Fund in the IT4Innovations National Supercomputing Center—path to exascale project (CZ 02.1.01/0.0/0.0/16-013/0001 791) within the Operational Programme Research, Development and Education, and IT4Innovations computational resources allocated within projects OPEN-11-33, OPEN-14-23, and OPEN-17-14.

《Compliance with ethics guidelines》

Compliance with ethics guidelines

Alexander Kovacs, Johann Fischbacher, Markus Gusenbauer, Harald Oezelt, Heike C. Herper, Olga Yu. Vekilova, Pablo Nieves, Sergiu Arapan, and Thomas Schrefl declare that they have no conflict of interest or financial conflicts to disclose.

Show More