《1. Introduction》

1. Introduction

In recent years, the coordination control of multi-agent-based cyber–physical systems has attracted considerable research attention due to theoretical breakthrough and wide-ranging engineering applications. Research topics in coordination control include consensus control [1], rendezvous control [2], flocking control, and formation control [3]. In addition, coordination control has a broad range of applications due to its efficiency and reliability, such as vehicle platooning, the formation of multiple unmanned aerial vehicles (UAVs), collaborative assembly systems [4], and sensor networks [5,6].

One central topic is the design of a distributed control law to stabilize a multi-agent system or reach a certain consensus, where each agent only uses local information from its neighbors for feedback [7]. Graph Laplacians play an important role in describing the interaction topologies and analyzing the stability of multi-agent systems [8,9]. The theoretical framework for proving the stability with graph Laplacians was introduced in the seminal work by Olfati-Saber et al. [10,11], where each agent of the multi-agent system is a single integrator. By extending this framework into double-integrator dynamics, Ren and colleagues [12,13] presented sufficient and necessary conditions for the stability of multi-agent systems from a graph-theoretic perspective, where the transformation of the Jordan normal form was applied to analyze the closedloop matrices. For high-order dynamics, Ni and Cheng [14] designed a stability algorithm based on the Riccati and Lyapunov inequality. Zheng et al. [15] proved the stability under interconnected topologies whose matrix has positive real eigenvalues using matrix decomposition and the Hurwitz criterion. Hong et al. [16] proposed a rigorous proof for the stability with an extension of LaSalle’s invariance principle. Beyond the abovementioned control law, Zheng et al. [17] also designed a distributed model predictive controller for multi-agent nonlinear systems and formulated a Lyapunov function to prove the asymptotic stability of a connected vehicle platoon. Wu et al. [18] presented a distributed sliding mode controller for multi-agent systems with positive definite topologies and exploited the asymptotic stability in the Lyapunov sense. Barooah et al. [19] introduced a mistuning-based control method to improve the stability margin of vehicular platoons. Ploeg et al. [20] developed an H-infinity control law to achieve the string stability of multi-agent systems.

The variation of interaction topologies is quite common due to link failures/creations in networks or obstruction between interactional agents. The stability of multi-agent systems under switching topologies has also attracted considerable research attention. For example, Tanner et al. [21] proposed a control law in combination with the attractive and alignment forces, which could stabilize the flocking system under dynamic topology. Olfati-Saber et al. [10] introduced a common Lyapunov function that could ensure the stability of single-integrator linear systems based on matrix theory and algebraic graph theory. Ren [12] considered a multi-agent system with double-integrator dynamics and showed that a set of connected, undirected, or directed topologies could stabilize the switching system by proving that the Lyapunov function is locally Lipschitz continuous. Ni and Cheng [14] expanded this study into a high-order integrator dynamic system and discussed the problem under the jointly connected undirected graph using Cauchy’s convergence criteria. Theoretically, the stability analysis of directed graphs is more challenging than the case of an undirected graph [10]. The methods for undirected topologies cannot naturally be applied to problems with directed topologies due to the lack of a positive definite property in directed topologies. In addition, it is more challenging to find a common Lyapunov function for switching directed topologies. Some pioneering studies have focused on the stability analysis of multi-agent systems with special switching directed topologies. For example, Qin et al. [22] analyzed a Lyapunov function of switching directed topologies systems and proved that system stability can be achieved under balanced directed graphs. Dong et al. [23] explored an explicit expression of the timevarying formation reference function and showed that the stability can be maintained if the dwell time is greater than a positive threshold.

This paper examines the stability and exponential convergence speed of general linear dynamic multi-agent systems under a class of directed switching topologies. A sufficient condition is presented by combining the transformation of the Jordan normal form and the common Lyapunov function. The unique contributions of this paper are two-fold. First, for the single- and double-integrator dynamics in Refs. [10,12], the Laplacian matrices of high-order dynamic systems are coupled with the number of agents, which causes the analysis methods used for single- and doubleintegrator systems to be non-applicable for general linear dynamics. In comparison, this paper considers the stability of a class of directed topologies whose eigenvalues are positive real numbers, and our result is applicable for multi-agent systems with general linear dynamic subsystems. Second, in comparison with the undirected topologies in Ref. [14], the positive definite property is more difficult to analyze because of the asymmetry in directed cases. The result in Ref. [22] cannot be applied to the directed topologies with positive real eigenvalues in this paper because the matrix （） is not always positive definite, in contrast to the balanced directed topologies discussed in Ref. [22]. The method proposed in this paper is suitable for topologies with positive real eigenvalues. The relationship between the topologies in this paper and balanced directed topologies is illustrated in Fig. 1.

《Fig. 1》

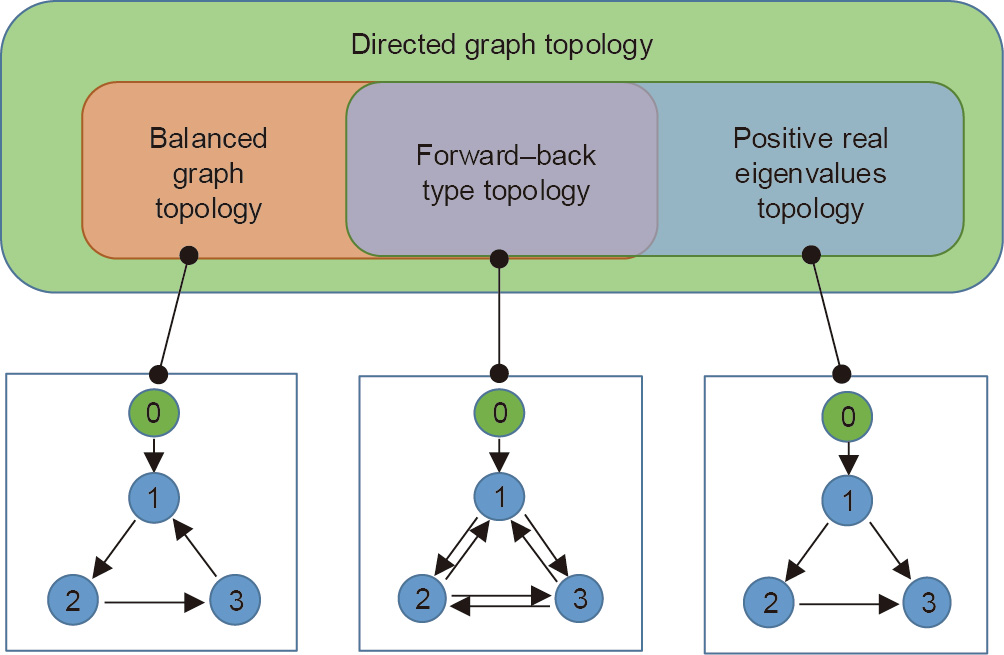
Fig. 1. A depiction of the relationship between the discussed topologies. Positive real eigenvalues topology has the property of all the eigenvalues of matrix （+P） being positive real. The followers in the forward–back topology can receive information from the same number of agents both forward and backward. It is clear that the forward–back type of topology is both a balanced graph and a positive real eigenvalues topology.

The rest of this paper is organized as follows: Section 2 introduces the algebraic graph theory. In Section 3, a class of positive real eigenvalues topologies is introduced and a linear controller designed with a common Lyapunov function and Riccati inequality is proposed. In Section 4, the stability and convergence speed of the closed-loop systems under switching topologies are proved. Section 5 illustrates the method through numerical simulation, and Section 6 concludes this paper.

《2. Preliminaries and problem statement》

2. Preliminaries and problem statement

This paper considers a multi-agent system that consists of one leader and N followers. The dynamics of each agent are homogeneous and linear. It is assumed that all the eigenvalues of the matrices describing the interaction topologies are positive and real numbers.

《2.1. Communication graph topology》

2.1. Communication graph topology

The information flow among agents is described by a directed graph topology 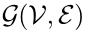with a set of N nodes  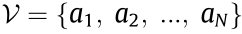, and a set of edges . The node ai denotes the ith agent, and each edge indicates a directed information flow between two agents.

The adjacency matrix is defined as E =  . with 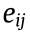 > 1 if 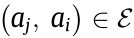; otherwise, 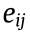=0 , where  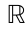denotes real number domain.  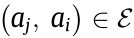means that agent j can obtain information from agent i . Self-edges   is not allowed, which means that =0 . Denote a neighbor set of node  as 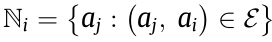. Define the Laplacian matrix  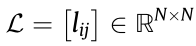as , .

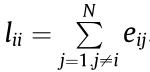To represent the information flow between the leader and followers, a pinning matrix   is defined as = diag , where = 1 if the agent can obtain the information from the leader; otherwise, =0. Based on the pinning matrix , a leader-reachable set could be defined as   if = 1; otherwise, 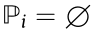. Then, an information-reachable set is defined as  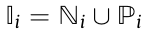to represent the nodes from which agent i can obtain information.

A directed path from to  is a sequence of edges in a directed graph of the form , where every edge  . A directed spanning tree is a directed graph, each node of which has exactly one parent except the root. A directed spanning tree 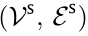  of the graph  is a subgraph of such that 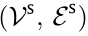 is a directed tree and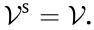 

《2.2. Agent dynamics》

2.2. Agent dynamics

The dynamics of each agent is:

where  denotes the state vector, 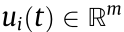 is the control input, n and m are the dimension of state and control variable respectively, A   and B  are the system matrix and input matrix, respectively. The system is assumed to be stable by choosing an appropriate value of the pair (A,B ).

The leader has the following linear dynamic:

where  is the state of the leader.

《2.3. Stability of multi-agent systems》

2.3. Stability of multi-agent systems

The objective of multi-agent consensus control is to make the state of each following agent consistent with that of the leader. For every agent 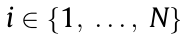, a distributed controller is required to realize

For the simplicity of the subsequent stability analysis, a new tracking error is defined as follows:

The state space function of the tracking error is

《3. Design of the controller》

3. Design of the controller

The interconnected topology of a multi-agent system varies with time due to some communication breakdown or obstacle between agents. In a switching topology problem, the information-reachable set of every agent varies with time. The notation 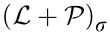is used to describe the time-dependence of information flow, in which is a switching signal at time t , and 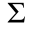is the index set of a group of graphs containing all the topologies. Consider an infinite sequence of nonempty time intervals 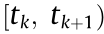; k = 0, 1, ... with  ; 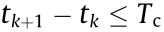for some constant Tc . It is assumed that 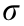is constant in each interval and the graph can be denoted as . In order to ensure stability under varying topologies, an appropriate controller and the graph set 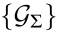are designed in this section.

《3.1. Linear control law》

3.1. Linear control law

For each agent, the controller is distributed and can only use the information from its information-reachable set . The following control law is used [24]:

where K 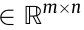 is a linear feedback gain. Substituting Eq. (6) to Eq. (5), the closed-loop dynamics of agent i can be obtained as follows:

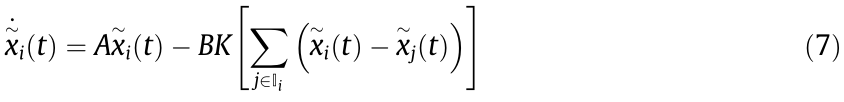
To describe the dynamic of the multi-agent system, the collective states of the system are defined as follows:

Recall the definition of Laplacian matrix and pinning matrix 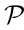; the closed-loop dynamics of the leader–follower multi-agent system are

where IN is the identity matrix and symbol is the Kronecker product. The overall closed-loop system matrix is defined as follows:

For a linear system, the stability is associated with the eigenvalues of the closed-loop system matrix. From Eq. (10), it can be seen that the eigenvalues of A c depend on . In other words, the interconnected topology influences the stability of the multi-agent system. In the following subsections, we will discuss a class of topologies that ensures that the eigenvalues of  are positive real numbers.

《3.2. Interconnected topologies with positive real eigenvalues》

3.2. Interconnected topologies with positive real eigenvalues

The method proposed in this paper is suitable for a topology with positive real eigenvalues that lacks an exact uniform mathe-matic description. Therefore, a specific type of topology with a positive real property is particularly focused on in this paper.

Lemma 1 [15]: Let ; 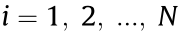, be the eigenvalues of , then all the eigenvalues are positive real numbers; that is, > 0; 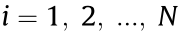, if there exists a directed spanning tree whose root is the leader and one of the following conditions holds:

(1) The interconnected topology of the following agents is the forward type; that is, 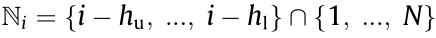, where hu and hl are the upper and lower bound of forward communication range respectively.

(2) The interconnected topology of the following agents is the forward–backward type; that is,  , where h is the communication range.

(3) The communication topology of the following agents is the undirected type; that is, j  .

Remark 1: For single-integrator or double-integrator dynamics, it is proved that switching directed topologies with a directed spanning tree is sufficient to stabilize the system; for example, see Refs. [10,12].

Remark 2: In Ref. [14], stability under the switching of jointly connected undirected topologies is discussed. Our paper considered directed topologies; disconnected conditions are not considered, and will be studied in further work.

Remark 3: The positive real eigenvalues and the positive definiteness of the matrix or matrices correlated with are important in analyzing the stability of multi-agent systems. In Ref. [22], balanced directed topologies are considered, whose Laplacian matrix has the property that is a positive definite matrix. A balanced and strongly connected graph can ensure that the spectral radius of is greater than zero [13], while the positive realness of the eigenvalues is not usually matched.

《3.3. Design of the coefficient matrix》

3.3. Design of the coefficient matrix

Since the pair (A, B ) is stabilizable, there exists a solution P > 0 for the following Riccati inequality:

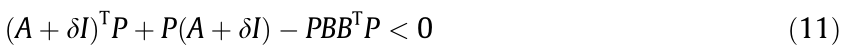
where δ is a positive number, which can be designed to influence the convergence of the system [25], and I is the identity matrix. The feedback matrix K can be constructed as follows:

where α is the scaling factor that satisfies the following:

where He (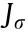)= 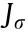+  ;  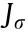is the Jordan canonical form of 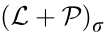, that is, = 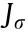; where  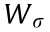is an invertible matrix and min  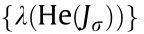denotes the minimum eigenvalue of He (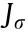) under all switching topologies. If the topology satisfies Lemma 1, it will be presented that He (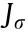) is a positive definite matrix. Before the theorem, the following lemmas will be introduced.

Lemma 2 [12]: Consider a matrix A = 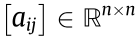. Then, all the eigenvalues of A are located within the union of n discs 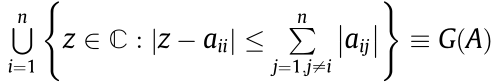, where denotes the complex number set and z is a complex number.

Lemma 2: is the well-known Gershgorin Disk Criterion.

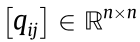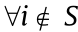Lemma 3 [26]: Consider a matrix Q =  and a set  . If there exists a nonzero sequence  for , and 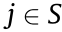, then Q is nonsingular.

Theorem 1: For the topology described in Lemma 1, is transformed to a Jordan diagonal canonical form J. Then He (J ) is a positive definite matrix.

Proof: For the topology defined as (2) and (3) in Lemma 1, matrix is real symmetric. It is obvious that He (J ) is positive definite, since J is a diagonal matrix. For the topology defined as (1) in Lemma 1, the eigenvalues of are larger than or equal to 1. J can be written as follows:

where 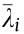 is the eigenvalue of , and 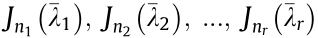 is the Jordan block of size . Then we have

For each block of He (J ), it has the following form:

According to the Gershgorin Disk Criterion, all the eigenvalues of He (J ) are not less than zero, since 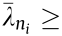1 and , where He (J ) = . According to Lemma 2, it can be determined that He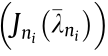 is nonsingular since  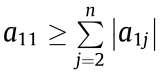and He 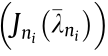is a triple diagonal matrix. Given that He (J ) is a quasi-diagonal matrix, He (J ) is also nonsingular. Then, all the eigenvalues of He (J ) are greater than zero. If He (J ) is symmetric, the result that He (J ) is a positive definite matrix can be proved. Table 1 presents the minimum eigenvalue of He (J ) for some typical topologies holding the conditions in Lemma 1. These topologies are described in Ref. [15], including: predecessor following (PF) topology, predecessor-leader following (PLF) topology, two predecessors following (TPF) topology, two predecessor-leader following (TPLF) topology, bidirectional (BD) topology, and bidirectionalleader (BDL) topology.

Remark 4: Theorem 1 shows that the minimum eigenvalue of He (J ) can influence the stability margin of the multi-agent system. It can be seen from Table 1 that the stability margin of the PF and BD topologies will get worse as the size N of followers increases, while the stability margin of the PLF, TPF, TPLF, and BDL topologies is independent of size N. The information from the leader is important for the stability margin of the system, and a suitable selection of topology, such as PLF and BDL, can improve the stability margin of the system. The result of the undirected topologies BD and BDL is the same as shown in Ref. [27]. A strict theoretical analysis will be conducted in future.

《Table 1 》

Table 1 min 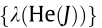of topologies.

《4. Stability under switching topologies》

4. Stability under switching topologies

It is obvious that for a finite switching system, stability can be realized if the final topology can stabilize the system with the control law proposed in Section 3. Under infinite switching conditions and under a class of topologies, the system will be stabilized with the control law shown in Eq. (6). The speed of convergence can also be ensured.

Lemma 4 [28]: Given a family of functions from to  , where 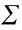is some index set. This can represent a family of systems . If all systems in the family share a common Lyapunov function, then the switching system 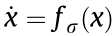is globally uniform asymptotically stable.

This theorem will be used to prove our main theoretical result. Before the proof, some lemmas in matrix theory will be introduced.

Lemma 5: Consider a positive definite real matrix M, and a positive real number < min 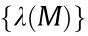, where 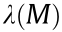denotes the eigenvalues of M. The matrix M – 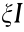is still positive definite.

Proof: If is an eigenvalue of M, there exists an eigenvector 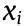 satisfying . Then, we have . Since 0 < < min 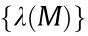, all the eigenvalues of M ? nI ð Þ are positive. It is obvious that (M – 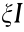) remains symmetric. Therefore, M – 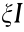is a positive definite matrix.

Lemma 6 [16]: Considering a stable linear constant system 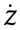=Hz, design its Lyapunov equation as 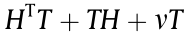= 0, where z is the state vector, H is the state matrix, 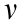is a positive real number and T is a positive defined solution of this equation. The Lyapunov function of this system is 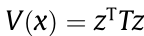, and the convergence speed of the system, 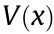, can be estimated by 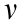; that is,  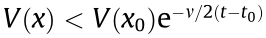, where t is the time of the system,  and 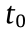 is the initial state and time of the system, respectively.

The main result of this paper is stated as follows.

Theorem 2: Consider a class of switching interconnected topologies , in which all the eigenvalues of  for every topology are positive real. For any 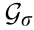, design the control parameters as shown in Eq. (12) and Inequality (13). Then, the switching system is globally uniform asymptotical stable with a common Lyapunov function 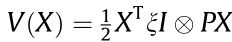. The convergence speed satisfies ,  where 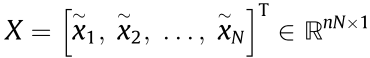 , N is the number of followers, n is the dimension of each agent, δ is the response coefficient, and .

Proof: Following the control law in Eq. (12) and Inequality (13), the following inequality can be obtained:

The closed-loop dynamics of the multi-agent system are

For a positive real topology, is transformed to a Jordan diagonal canonical form. The closed-loop dynamic matrix can also be transformed to a diagonal block matrix:

Substituting Inequality (13) into Eq. (19), we have

is still symmetric. He 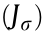is a positive definite matrix, according to Theorem 1.

According to the Lemma 5, the inequality can be derived as follows:

Multiplying 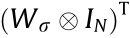and on the left and right parts of the left side of the inequality, respectively, yields a new inequality:

The following inequality can be derived according to Lemma 5:

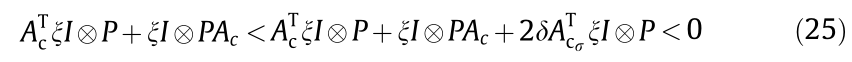
  is the common Lyapunov function of the system with a positive real topologies family. Inequality (25) ensures the stability of the switching systems. According to Lemma 6, the rapidness of the system can be estimated by δ ; that is, .

Remark 5: Compared with Ref. [22], the topologies discussed in Theorem 2 do not need to be a balanced graph, which expends the family of directed topology under the switching condition. A typical forward topology such as PF is not a balanced graph (e.g.,  in Fig. 2). Furthermore, the dwell time has no effect on the stability of the controller in Theorem 2, in contrast to the result in Ref. [23].

Remark 6: In practice, the switching topologies may be unknown, which makes the selection of α nontrivial. A larger α is helpful to stabilize the switching system in this situation. In fact, Inequality (13) is only a sufficient condition for the system stability, which ensures the stability in theory. In our simulation, an α inconsistent with this inequality can also stabilize the system.

《Fig. 2》

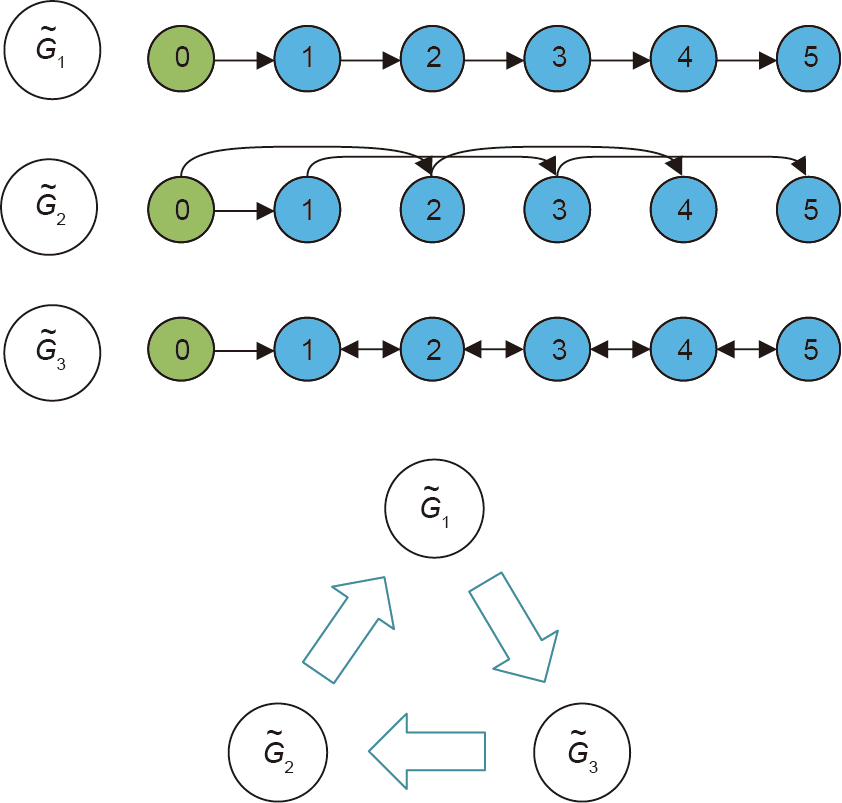
Fig. 2. Switching topologies , , and 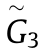are all positive real eigenvalue topologies.  and are the forward type and 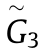is the forward-back type. In the simulations, the topology switches among these three topologies.5. Simulation results

The vehicle platoon is a typical multi-agent system, which has attracted increasing attention because of its benefit in traffic [24]. The matrices of typical topologies that describe the information flow among the vehicles in a platoon have positive real eigenvalues [15]. We conducted simulations of a homogeneous platoon with six identical vehicles (one leader and five followers) in order to validate the effectiveness. For platoon control, a thirdorder state space model is derived for each vehicle [17]:

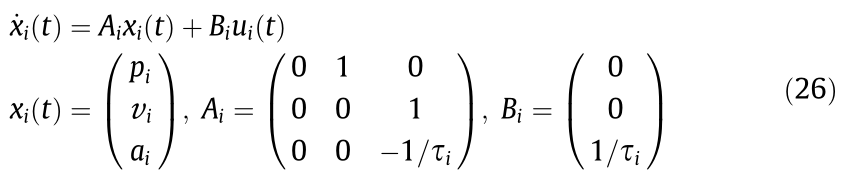
where denote the position, velocity, and acceleration of each vehicle; and is the inertial delay of the vehicle longitudinal dynamics, which is set as 0.4 s in the simulations. The information flow topologies are illustrated in Fig. 2, the matrices’ eigen-values of which are all positive real numbers. The topology of the system is set to switches every 2 s periodically from   to , , 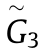and then  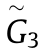to , as shown in Fig. 3. The initial speed of every vehicle is 20 m·s-1 , and the position error is randomly distributed in the interval [–10 m, 10 m]. The leader is set to continuously run at 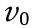= 20 m·s-1.

《Fig. 3》

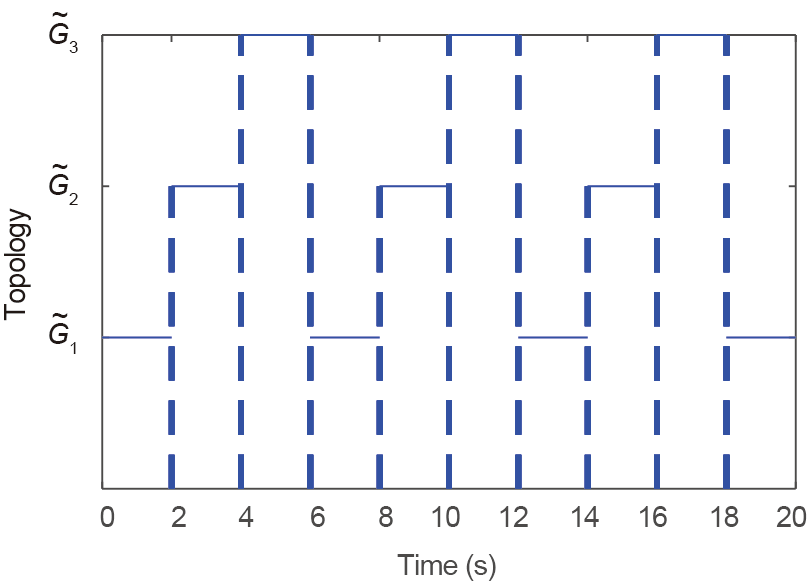
Fig. 3. Switching signal. The dwell time is set as 2 s.

The eigenvalues of He (J ) for the three topologies are listed in Table 2. All the eigenvalues are positive real and, considering their minimum value, the scaling factor α can be chosen to be 10. Three scenarios have been simulated, with two stable scenarios of differentresponsecoefficients δ andoneunstablescenario.Thecontroller parametersinScenarios1 and 2are designedasinTheorem2. However, the parameters in Scenario 3 do not satisfy the stability condition in Ref. [15]. All the parameters are listed in Table 3.

《Table 2》

Table 2 Eigenvalues of He (J ) for , , and .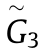

《Table 3》

Table 3 Controller parameters.

Fig. 4 shows the state error of the vehicle platoon under the switching topologies. The simulation result shows that the control law designed according to Eq. (12) and Inequality (13) can stabilize the vehicle platoon. Compared with Fig. 5, it demonstrates that a larger d tends to make the system converge to the stable state more quickly. Fig. 6 illustrates the performance of a controller whose parameters are chosen as the unstable region criterion in Ref. [15], which can show the effectiveness of our controller design method. It should be noted that Theorem 2 is only a sufficient condition for the system stability, which means that the selection of controller parameters—that is, if α does not meet the condition of Inequality (13)—may also stabilize the switching system.

《Fig. 4》

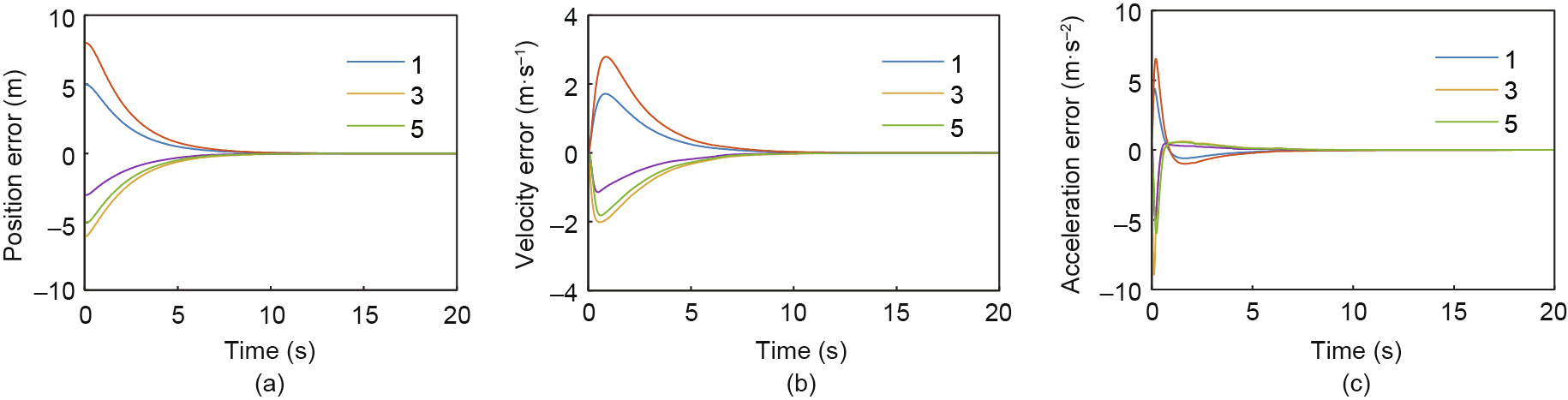
Fig. 4. Stability performance under switching topologies with δ = 0.5. (a), (b), and (c) show the tracking error of the position, velocity, and acceleration, respectively. The switching system achieved stability in 15 s.

《Fig. 5》

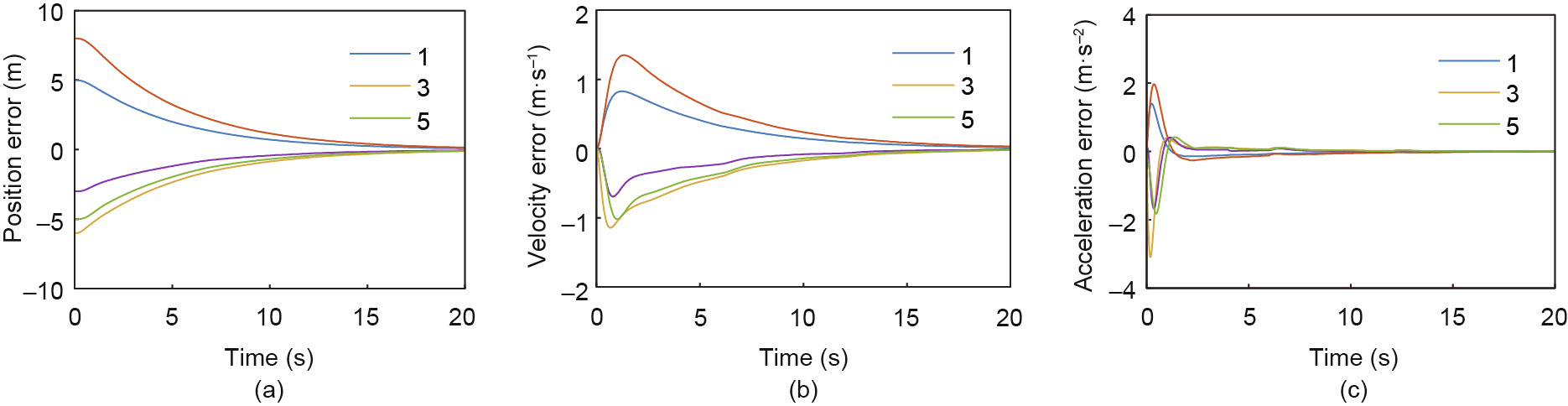
Fig. 5. Stability performance under switching topologies with δ = 0.2. (a), (b), and (c) show the tracking error of the position, velocity, and acceleration, respectively. Compared with the controller in Scenario 1, this controller tends to have a longer convergence time of about 25 s.

《Fig. 6》

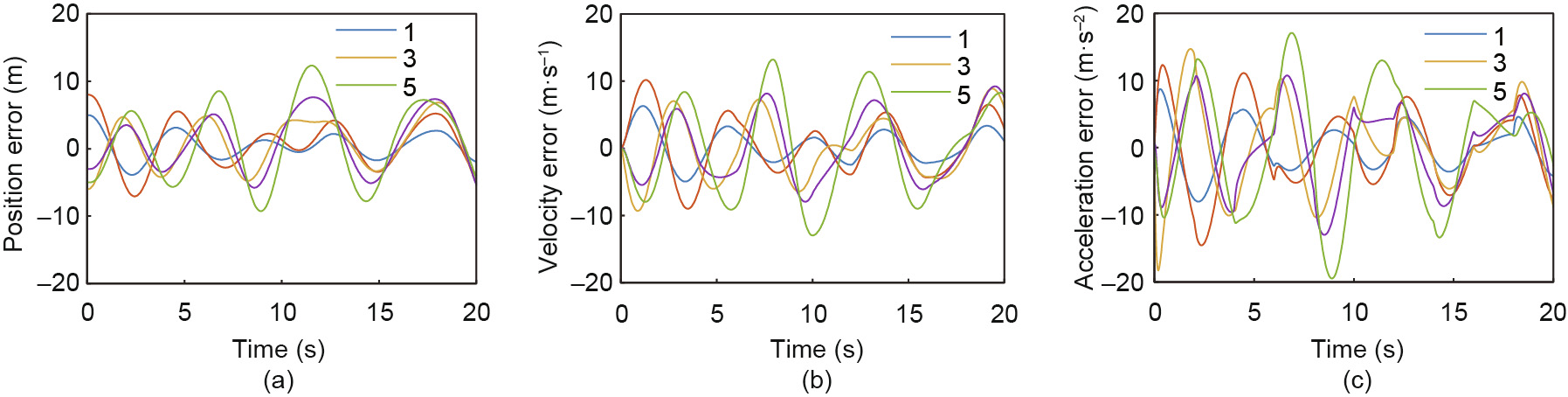
Fig. 6. Stability performance under switching topologies with an unstable controller. (a), (b), and (c) show the tracking error of the position, velocity, and acceleration, respectively. The parameters are designed from the unstable region presented in Ref. [15]. This illustrates the effectiveness of our controller design method.

《6. Conclusions》

6. Conclusions

This paper examines the stability of multi-agent systems under a class of switching topologies, where all the eigenvalues of  matrices are positive real numbers. Graph theory is used to describe the interconnected topology. The Hurwitz criterion and Riccati inequality are applied to design the control law in order to stabilize the multi-agent system and adjust the convergence speed of the system. By using the common Lyapunov function theorem, the stability of switching topology systems is proved. We have shown that stability can be achieved if the matrices’ eigenvalues of all the topologies are positive real numbers and present a sufficient condition for the switching system. The exponential stability and convergence speed can be influenced by the response coefficients d in our controller.

《Acknowledgements》

Acknowledgements

This work is supported by International Science and Technology Cooperation Program of China (2019YFE0100200) and Beijing Natural Science Foundation (JQ18010). It is also partially supported by Tsinghua University–Didi Joint Research Center for Future Mobility.

《Compliance with ethics guidelines》

Compliance with ethics guidelines

Shengbo Eben Li, Zhitao Wang, Yang Zheng, Diange Yang, and Keyou You declare that they have no conflict of interest or financial conflicts to disclose.