《1　前言》

1　前言

计算机辅助几何设计中有很多经典的曲线造型工具，如 Bezier 曲线、B 样条曲线等。此类经典的曲线模型具有许多优良的性质，在实际工程中也得到了广泛应用。但其有许多不足之处，如 B 样条曲线只能表示多项式曲线，对于 CAD/CAM 中常见的曲线如圆、摆线、双曲线等，它只能近似表示。且对于给定的控制点，均匀 B 样条曲线的位置是确定的。若调整曲线的形状，必须调整控制多边形。

为了克服这些局限，很多文献中提出了新的模型，如张纪文提出了由｛sin t，cos t，t，1｝的线性组合得到的 C - B 样条曲线[1,2]。C - B 样条曲线是三次均匀样条的一个推广，且可以精确地表示椭圆和圆弧段。Mainar 等人在空间 Span ｛sin t，cos t，t 2，t，1｝和 Span ｛1，t，cos t，sin t，t cos t，t sin t｝上给出正规 B 基[3,4]。文献 [5] 中构造了二次带形状参数的曲线，可以在控制多边形不变的情况下，调节参数的大小来调节曲线形状，形状参数的调整范围为［-1，1］。但是以上模型都是针对低阶情况，因此文献 [6] 给出了构造任意阶曲线的模型，构造了类拟 Bezier 曲线，文献 [7] 构造了任意阶的 NUAT 样条曲线，但它们存在的问题是对于固定的控制点，其样条曲线是固定的，必须调整控制多边形，才能调整曲线的形状。

笔者提出了更一般的 k 阶（ k 2） 指数多项式样条模型，它具有 G 2 连续、凸包性、局部性、归一性、对称性等 B 样条的优良性质，并且增加一个可调节的参数，它能生成不同位置的曲线，可在控制多边形不变的情况下，更好地逼近控制多边形，同时参数的取值范围大于［-1，1］。

《2　指数多项式样条基函数的构造性质》

2　指数多项式样条基函数的构造性质

记 ti  = ｛i ：i = 0，± 1，± 2，… ｝ 为对参数 t 轴作均匀分割得到的一组节点。记在节点处达到 k -2（ k 2）阶连续的分段 k 阶指数多项式的空间为 Ωk，Ωk 是一线性空间。在空间 Ωk （ k 3）上给出一组基，这组基具有与均匀 B 样条基相同的性质，如正性、归一性、对称性和局部支集性等，称为指数多项式均匀样条基。

考虑到正性、归一性、对称性等性质，首先定义二阶基函数为

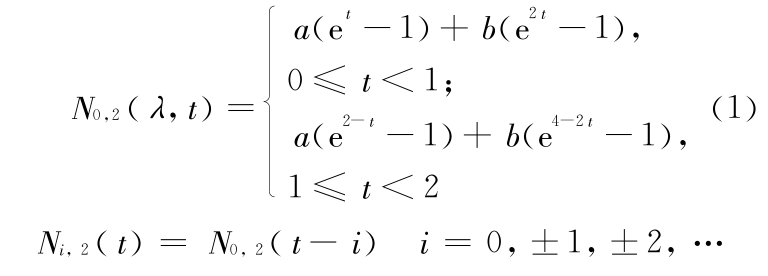
是 t ∈ ［0，2］ 内关于 t = 1 对称，且 C 0 连续（零阶点连续） 的分段二次函数，在区间端点间 N（ λ，0） = N（ λ，2） = 0。同时为满足 k 3 时 Ωk 上的基函数的归一性，须满足条件

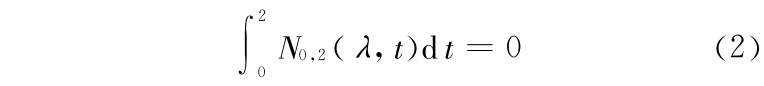
由式（1）和式（2）得到

若令 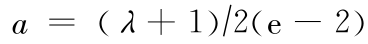，则 b = – λ /（e2- 3）。将 ，b 代入上式，得到公式

　当 k 3 时，定义下列递推公式

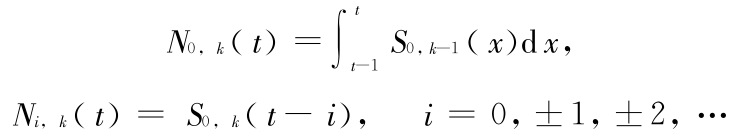
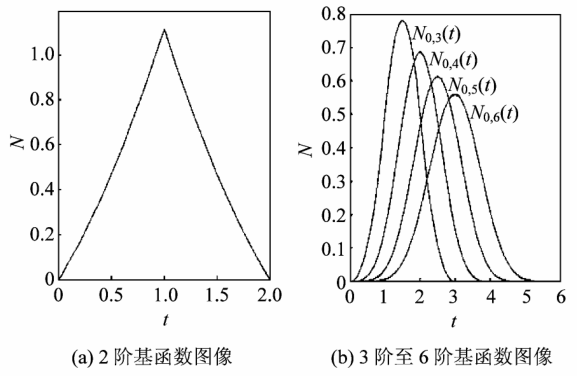
称 Ni,k （t） （ i = 0，± 1，± 2，… ） 为 k 阶指数多项式均匀样条的基函数，其中 为形状可调节的参数，其取值范围为［–（e2 – 3）/（e2 – 4e + 5），（e2– 3）/ （e2– 2e – 1）］。在实际应用中，可以根据需要确定其具体取值。当 k 3 时，根据上述定义可以得到 Ni,k （t） 所具有的性质，说明 Ni,k （t） 为空间 Ωk 的一组基。图 1 分别显示了 2 阶指数多项式均匀样条基函数和 3 ~ 6 阶的指数多项式均匀样条基函数图像，其中 = 0.3。

《图1》

图1　各阶指数多项式均匀 B 样条基函数的形状

Fig.1　Various figures of basis function of exponential polynominal uniform spline

定义中给出的形状参数 的取值范围，是指 Ni,2 （t） 中形状参数的取值范围。为满足 Ni,2（t） 非负性，需保证 t ∈ （0，1） 时，（et – 1） + b（e2t – 1）≥ 0，由此求得 的取值范围为 ［ –（e2– 3）/（e2– 4e+ 5），（e2– 3)/（e2– 2e – 1）］。际上随着阶数的增加，形状参数的取值范围还可以扩大。图 2 为形

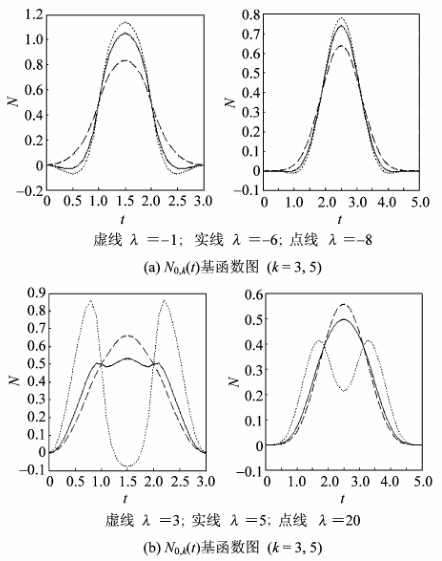
状参数 取不同值时，3 阶和 5 阶指数多项式基函数比较图。表 1 给出了 2 ~ 6 阶指数多项式的形状参数 取值范围。

《图2》

图2　 取不同值 N0,k 基函数图 （k = 3，5）

Fig.2　Figures of basis function of N0,k ( t ) with different values of   (k = 3,5)

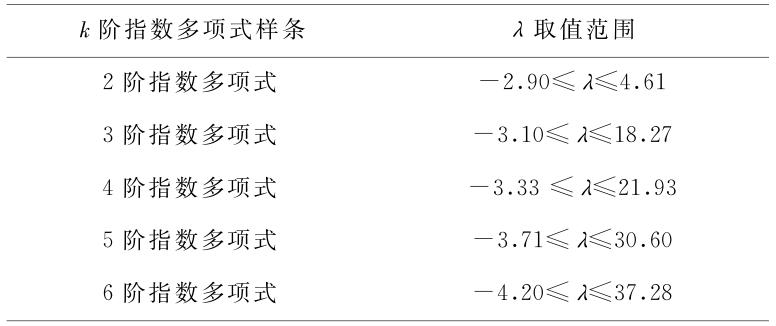
《表1》

表1　形状参数 的取值范围

Table 1　The range of the shape parameter

从图 2（a）可以看出对于固定的 k，当 ＜ 0 时，随着 λ 的减小，超出取值范围后基函数变为负数，但随着阶数 k 的增加，其函数图像最终变为非负。图 2（b）可以看出，对于固定的 k，当 ＞ 0 时，随着 λ 的增大，指数多项式均匀样条基函数出现多峰现象，最终出现负值，但随着阶数 k 的增加，其函数图像最终变为单峰和非负。

k 阶指数多项式均匀样条基函数具有如下性质。

性质 1　非负性

由定义知对于 t ∈ （- ∞，+ ∞ ），Si,2 （t） 0，由公式  可得

类推得 ，再由定义公式可得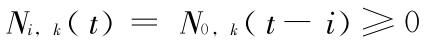 

性质 2　局部支集性

性质 3　归一性

证明　对于 t ∈ ［ i，i + 1］，

当 k = 3 时 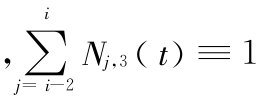 显然成立。

假设当 n = k  成立，即 。则当 n = k + 1 时，

性质 4　求导公式

即 。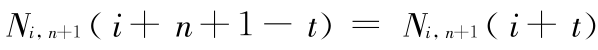

性质 5　对称性 Ni,k（i + k - t） = Ni,k （i +t）。

证明当 k = 2 时 Ni,k（i + k - t） = Ni,2（i + 2 - t） = N0,2（2 - t）Ni,k（i + t） = Ni,2（i + t） = N0,2（t）。

由定义构造条件 1 可知，N0,2（2 - t） = N0,2（t），故当 k = 2 时，Ni,k（i + k - t） = Ni,k（ i +t）。假设当 k = n 时，Ni,k（i + n - t） = Ni,k（i +t） 成立，故 N0,k（n - t） = N0,k（t） 则当 k = n + 1 时，t ∈ 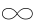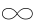（- ，+ ）上线性无关。当 t ∈ （ i，i + 1），同理可证。

性质 6　连续性 Ni,k（t） 在整个参数空间上为 k- 2 阶连续

证明由定义知 Ni,2（t） 零阶连续，则 Ni,3（t）一阶连续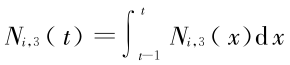，2 阶连续，由此可推出为 k - 2 阶连续。

性质 7　线性无关性

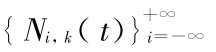 （ i ＝ 0 ， ± 1 ， ± 2 ， … ）在 t ∈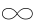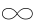（－ ，＋）上全局线性无关，特别地在 t ∈ （ i，i -1） 上 Ni -k + 1 （t），…，Ni,k （t） 局部线性无关。

证明　当 k = 2 时显然成立。假设当 k = n 时 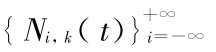（ i ＝ 0 ， ± 1 ， ± 2 ， … ）在 t ∈ 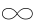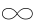（- ，+ ） 上线性无关，则当 k = n + 1 时，令 ，两边求导可得= 0，由性质 4 可得

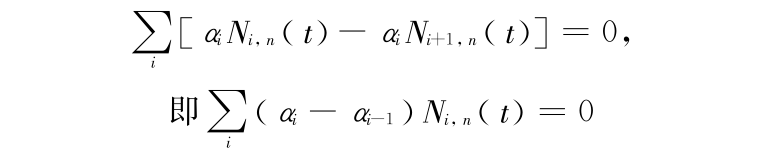
由于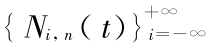在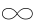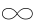（ - ，+ ） 上线性无关，所以 （i = 0，± 1，± 2，… ）

代入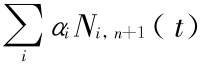= 0 ，得

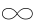= 0，故 α = 0。所以 （i = 0，± 1，± 2，… ）在 t ∈（- ，+ ） 上。

《3　指数多项式均匀样条曲线》

3　指数多项式均匀样条曲线

假设 ，m = 2，3，Ni,k （t） （ i =1，2，3，…，n） 是定义在［，b］上的 k 阶指数多项式均匀样条基函数，设 = k，b = n + 1，则 N1,k（t），N2,k（t），N3,k（t），…，Nn,k（t） （n k）是空间 Ωk ［，b］ 的一组基，如图 3 所示。空间 Ωk［，b］ 中的曲线为

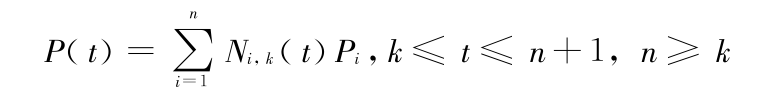
其中 ｛Pi∶i = 1，2，3，…，n｝ 为控制顶点，P1 P2 P3 … Pn 为控制多边形。图 4 为 n = 5 时，两条指数多项式均匀样条曲线。

《图3》

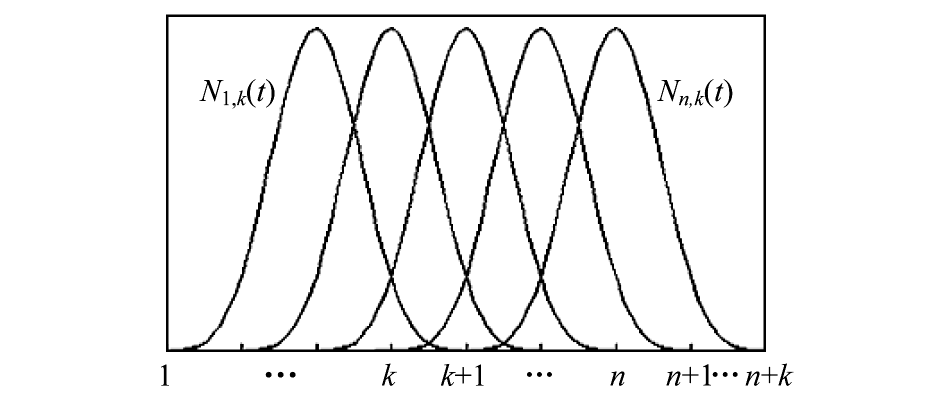
图3　N1,k（t），…，Nn,k（t）是空间 Ωk ［，b］的一组基

Fig.3　Set of basis N1,k（t），…，Nn,k （t） in Ωk ［，b］

《图4》

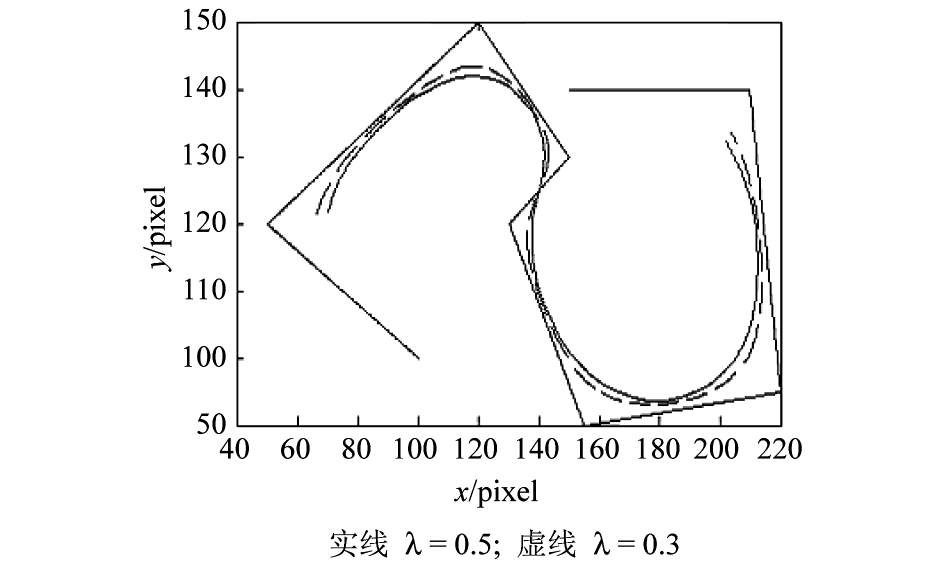
图4　4 阶指数多项式均匀样条曲线

Fig.4　4 order exponential polynomial uniform spline curves

性质 8　凸包性

由基函数的归一性，曲线 P（t） （ i t i + 1）位于 k 个控制点 Pi -k +1，…，Pi  的凸包 Hi  内，整条曲线 Pi  （ i t i + 1） 位于这些凸包 Hi  的并集 H  之内。

性质 9　保凸性

凸控制多边形 P1 P2  … Pn  定义的曲线 P（t） 为凸曲线。

性质 10　几何不变性和仿射不变性

曲线的形状、位置与坐标系的选择无关，曲线做仿射变换，只须把其控制多边形作此仿射变换。

性质 11　局部调整性

由曲线的表示公式，改动一个控制顶点  Pi （i t n），曲线上仅有点 Pi  参加的控制的那 L 段（ l k） 曲线的形状发生变化。同样，曲线 P（t） （ i t  i + 1） 上的点只与 k 个控制顶点 Pi -k +1，Pi -k +2，…，Pi 有关，便于交互设计。t ∈ ［ i，i + 1］ 区间内子曲线可以表示为

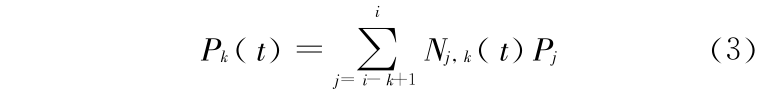
性质 12　曲线求导公式为

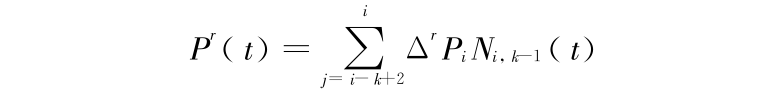
证明

对于曲线 P（t） 在 t  ∈ ［ i，i + 1］ 区间内子曲线，则

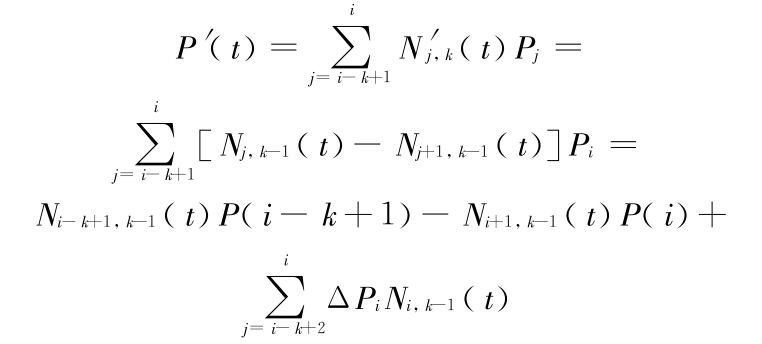
根据性质 2，t ∈ ［ i，i + 1］时，Ni -k+ 1,k -1（t） = Ni + 1,k - 1（t） = 0，故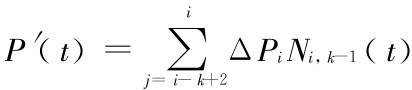，其中 Δ Pi = Pi  - Pi -1。则

其中 Δr Pi = Δr -1Pi  - Δr -1Pi -1。

性质 13　对称性

以 P1 P2  … Pn 为控制顶点的的 k 阶指数多项式均匀 B 样条曲线与 Pn，Pn-1，…，P1 为控制顶点的 k 阶指数多项式均匀 B 样条曲线为同一条曲线，但方向相反。即

《4　指数多项式样条曲线的逼近性》

4　指数多项式样条曲线的逼近性

以 3 阶指数多项式均匀样条为例，分析在参数 取不同值时，曲线与控制多边形的逼近关系。当 t ∈ ［0，1］时一般的根据式（3）得到曲线的在 t ∈［0，1］的子曲线，考虑到指数多项式均匀样条为 3 阶，控制顶点与曲线上对应点有

两边计算并取范数有

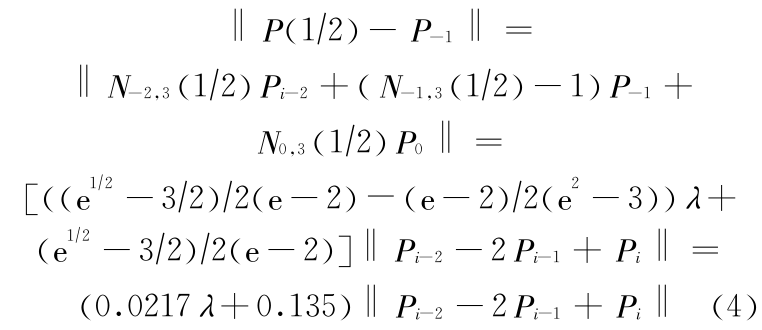
从式（4） 可以得知，当形状参数 越大，则 P（1/2） 和 P-1 的距离越大 ；反之 越小，两者距离越小。类似地可以得到，整个参数区间内，随着形状参数 减小，三阶指数均匀样条曲线更加逼近控制多边形顶点。

同样可以推导，随着形状参数 的减小，k（ k  3）阶指数均匀样条曲线更加逼近控制多边形顶点（证明过程略）。图 5 给出了形状参数 取值不同时，曲线与控制点的逼近情况。

《图5》

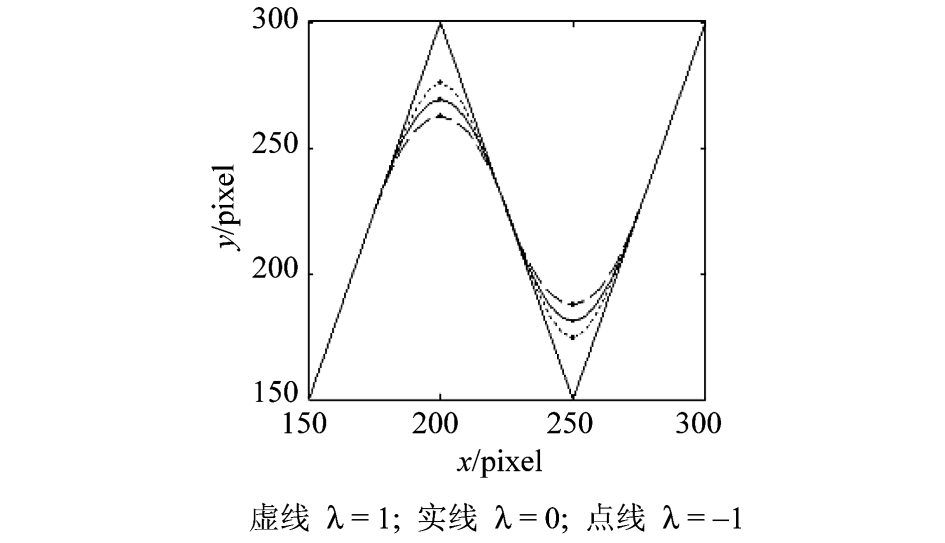
图5　三阶指数多项式均匀样条曲线逼近

Fig.5　Approach of 3 order exponential polynomial uniform spline curves

《5　指数多项式样条曲线的图形实例》

5　指数多项式样条曲线的图形实例

曲线设计中的一个基本的内容是开曲线和闭曲线的构造，了解开曲线的端点行为和闭曲线的构造具有重要意义。对于控制点列 Pi （ i = 1，2，…，n），其中 P0 = Pn，若要构造开曲线，只须增加 2 个控制点 P0 = 2P1 - P2，Pn+ 1 = 2Pn - Pn-1，即可构造两端插值于 P1，Pn，且在 t0 和 tn 处分别以 P1 -P2，Pn - Pn-1 为切向量的开曲线。若要构造闭曲线，只须增加 2 个控制点 Pn+1 = P2，Pn+2 = P3。图 6 给出了 取不同值时的开曲线和闭曲线。图 6（a）是 = -2，-1，0，2，4，6 时，按控制点列生成的花瓣开曲线图形 ；图 6（b）是 = -4，-2，-1，0，2，4，6，8 时，按控制点列生成的花纹闭曲线图形。不论是开曲线还是闭曲线，调整 的值可以得到不同的曲线。当 增大时，曲线逐渐远离控制多边形，当 减小时，曲线逐渐逼近控制多边形。

《图6》

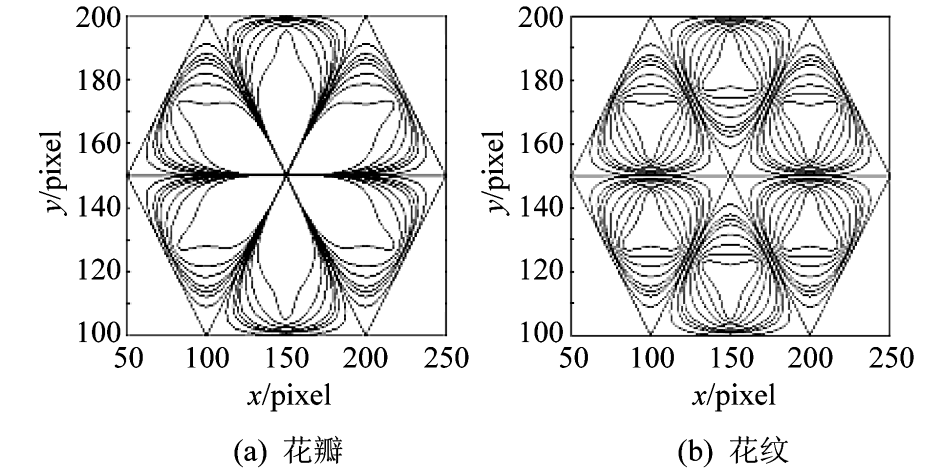
图6　4 阶指数多项式均匀样条曲线造型图

Fig.6　Figures of 4 order exponential polynomial uniform spline curves

《6　指数多项式均匀样条曲面构造》

6　指数多项式均匀样条曲面构造

给定 （ m + 1） × （ n + 1） 个控制顶点 di,j （ i =0，1，…，m ； j = 0，1，…，n）的阵列，构成一张控制网格。又分别给定指数多项式样条基函数阶数为 k 与 l，和 2 个节点矢量 U = ［ u0 u1 … um+k+1 ］ 与 V = ［ v0 v1 … vm+k+1 ］，则定义了 k × l 阶张量积指数多项式样条曲面。方程为

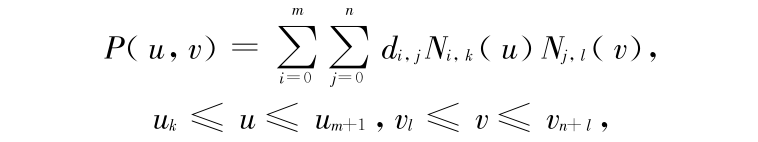
其中指数多项式均匀样条基 Ni，k，Nj,l 均由定义递推公式得到。当 m = n 时的特殊情况，得到双 n 阶的指数多项式样条曲面。指数样条曲线的局部性质可以推广到曲面。因此，vj v vj  定义在子矩形区域 ui u ui+1，vj v vj+1 上的那块子曲面片仅和控制点阵中的部分顶点 de,f （ e = i - k，i - k + 1，…，e ； f = j - l，j - l + 1，…，j） 有关，与其他顶点无关。相应上述曲面方程可以改写成为分片表示形式 ：

类似于 B 样条曲线性质向 B 样条曲面推广，指数均匀样条曲线的性质都可推广到指数均匀样条曲面。图 7 为 取不同值时，双 4 指数均匀样条曲面的造型图。

《图7》

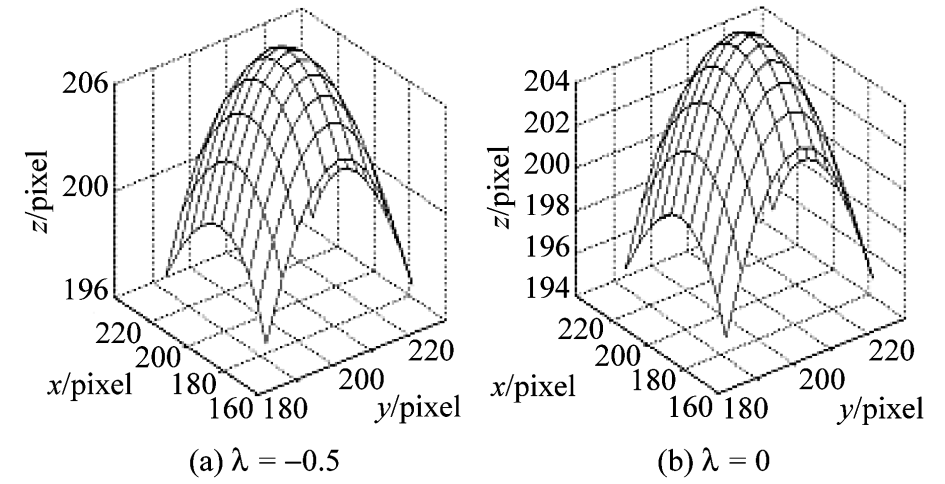
图7　双四阶指数多项式均匀样条曲面

Fig.7　Double 4 order exponential polynomial uniform spline surface

《7　结语》

7　结语

构造了 k（ k 3） 阶指数多项式的均匀样条基，并因此定义了指数多项式均匀样条曲线和曲面。该样条基具有与均匀 B 样条基相同的性质、结构，保持了均匀 B 样条曲线的一些实用的几何性质。并且该样条基带有一个形状参数，通过对形状参数取值的改变，可以调整曲线接近其控制多边形的程度。同时该样条曲线可以构造张量积曲面，通过选取形状参数的值，也可以得到不同程度地接近其控制多面体的曲面。指数多项式均匀样条定义线性空间 Ωk 上，又由于 Ωk 对于积分运算是封闭的，即对任意的 N（t） ∈ Ωk，有 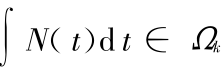，为相关的积分运算带来方便。以上分析说明指数多项式均匀样条模型是自由曲线曲面造型的一个有力工具，具有良好的应用价值。