Interaction Effects Between Wave and Two Connected Floating Bodies

Abstract

In this paper, boundary integral equation method is used to study the hydrodynamic interaction effects between wave and two connected floating structures. The hydrodynamic interaction between the two bodies is considered. The amplitudes of the body motions are determined according to the motion equations of the two bodies and the continuous conditions at the connection between the bodies. In order to verify this method, the heave amplitude at the hinged joint and the relative angular deflection of two floating barges, which connected by a hinge, are calculated and compared with the results from Newman. The comparison shows that the present calculation agrees well with Newman's result except at the nearby of the resonant frequency of the system. At the resonant frequency of the hinged system the present result changes quickly, but Newman did not mention the phenomenon.

Content

《1 前言》

1 前言

多体系统在固体结构中有较早的研究, 如机械和航空航天领域。与固体结构相比流体中的多体结构更为复杂, 主要体现在结构与流体间的耦合和结构之间的干涉上。

在2个物体水动力相互影响的问题上, Kodan^[1] 采用切片理论研究了斜向波浪作用下2个平行细长物体的水动力影响。Fang和 Kim^[2] 也采用切片理论将2个漂浮平台结构按二维问题处理, 然后应用奇点分布法计算了2个物体间的相互作用和影响。Kokkinowrachos等^[3] 用奇点分布法计算了2个物体上的漂移力, 并和实验数据进行了比较。Lee 和Choi^[4]也采用奇点分布的方法计算了波浪与漂浮的生产存储或装卸系统 (FPSO) ——运输油轮系统的相互作用问题。Chen和 Mahrenholtz^[5] 则运用了边界积分方法, 计算了二维情况下由弹簧连接的2个漂浮半圆柱的相互作用, 由于他们没对积分方程中的固角值做特别处理, 该方法仅适用于光滑物体, 在连接方式上缺少通用性。Newman^[6] 也采用边界积分的方法, 计算2个相同的漂浮方箱铰连接运动响应, 对于这一特殊的结构形式他把2个铰接方箱作为有7个自由度的系统来计算, 可以大量地降低计算机的计算量和存储量, 但也限制计算方法的通用性, 使其无法应用于以不同方式连接的不同尺寸、不同形状的多浮体问题。沈庆、陈徐均^[7] 在求多浮体系统的波浪运动响应时, 把铰连接的多浮体系统作为铰连接无根数系统, 用多刚体力学方法进行运动学分析, 这种方法主要考虑了浮体系统的运动学方程, 但没有考虑浮体间的水动力影响。此外Leonard等^[8] 、Chen等^[9] 也用有限元法来计算两物体系统。

笔者采用边界积分的方法, 计算2个浮体组成的浮体系统在规则波作用下运动响应的频域解。通过边界积分方程求出系统的辐射势, 进而求出物体运动时产生的附加质量和辐射阻尼。由于2个物体的相互作用, 所以作用在每个物体上的附加质量和辐射阻尼都由两部分组成。设系统内有A, B两物体, A物体受到的附加质量和辐射阻尼一部分是A物体自身运动产生的, 另一部分则是由系统内另一物体B运动而对A产生的。边界积分方程采用Teng和Eatock Taylor^[10] 的方法得到, 应用高阶边界元法并在物体内部增加积分方程以消除奇异积分和固体角, 这种方法可得到任意2个物体组成的系统在规则波作用下的水动力影响及运动响应的频域解, 适用于任意形状的物体及任意的连接方式。高阶边界元法可减少网格的划分数量, 节省计算时间, 提高计算精度。

《2 积分方程》

2 积分方程

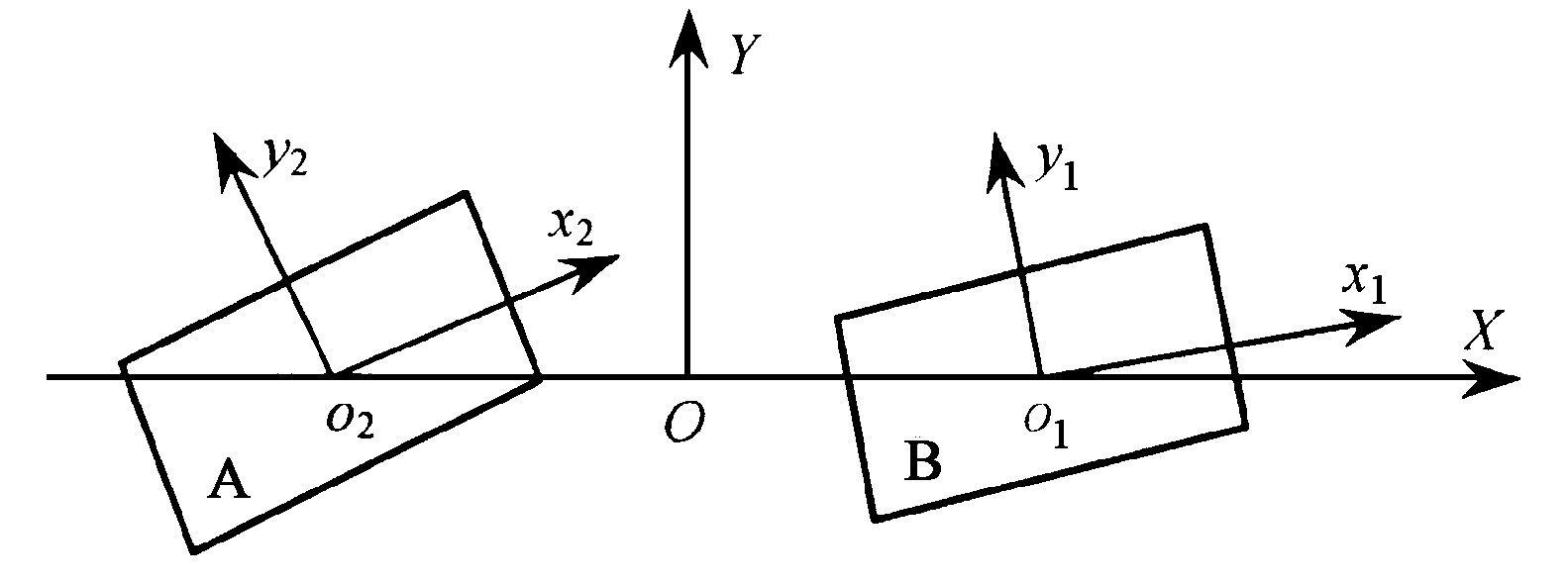
假定流体为无旋、无粘、不可压缩的理想流体, 流体满足势流理论, 入射势已知, 波高足够小, 波浪满足线性理论。考虑2个浮体通过某种方式连接在一起组成的系统 (见图1) , 整体坐标和2个局部坐标的选取见图2。

《图1》

图1两物体连接示意图

Fig.1 Sketch of two connected barges

《图2》

图2整体坐标和局部坐标示意图

Fig.2 Coordinate systems

对水深d中2个二次可导的函数u和v, 应用第二格林公式可得积分方程

$\underset{Ω}{\int \int \int} [u Δ^{2} v - v Δ^{2} u] d V = \underset{S}{\int \int} (u \frac{\partial v}{\partial n} - v \frac{\partial u}{\partial n}) d S (1)$ $\underset{Ω}{\int \int \int} [u Δ^{2} v - v Δ^{2} u] d V = \underset{S}{\int \int} (u \frac{\partial v}{\partial n} - v \frac{\partial u}{\partial n}) d S (1)$

其中S=S_B+S_F+S_D+S_∞, S_B为物面, S_F为自由水面, S_D为水底面, S_∞为无限远处水柱面, n为物面的单位法向量, 指出流体为正。

令ϕ=u为速度势函数, G=v为源点在 (x₀, y₀, z₀) 的格林函数, 满足下列控制方程和边界条件:

$\begin{array}{l} Δ G (x, x_{0}) = δ (x - x_{0}) δ (y - y_{0}) δ (z - z_{0}), \\ - d < z < 0 ‚ \\ G_{z} = ω^{2} G / g, z = 0 ‚ \\ G_{z} = 0, z = - d ‚ \\ G_{r} = 0, r \to \infty (2) \end{array}$ $\begin{array}{l} Δ G (x, x_{0}) = δ (x - x_{0}) δ (y - y_{0}) δ (z - z_{0}), \\ - d < z < 0 ‚ \\ G_{z} = ω^{2} G / g, z = 0 ‚ \\ G_{z} = 0, z = - d ‚ \\ G_{r} = 0, r \to \infty (2) \end{array}$

式中 $Δ^{2}$ $Δ^{2}$ 是拉普拉斯算子符, δ (*) 是狄拉克函数, 满足上述条件的格林函数G由John (1950) 导得

$\begin{array}{l} G = - \frac{1}{4 π} (\frac{1}{r} + \frac{1}{r_{31}}) + \\ \frac{1}{4 π} \int_{0}^{\infty} \frac{2 (v + μ) e^{- μ d} \cosh μ (z + d) \cosh μ (z_{0} + d)}{v c o s h μ d - μ \sinh μ d} \cdot \\ J_{0} (μ R) d μ \end{array}$ $\begin{array}{l} G = - \frac{1}{4 π} (\frac{1}{r} + \frac{1}{r_{31}}) + \\ \frac{1}{4 π} \int_{0}^{\infty} \frac{2 (v + μ) e^{- μ d} \cosh μ (z + d) \cosh μ (z_{0} + d)}{v c o s h μ d - μ \sinh μ d} \cdot \\ J_{0} (μ R) d μ \end{array}$

其中 r=[R²+ (z-z₀) ²]^1/2, r₃₁=[R² + (z+z₀+2d) ² ]^1/2, v=ω²/g, R=[ (x-x₀) ²+ (y-y₀) ²]^1/2, 则积分方程可写为

$\begin{array}{l} α ϕ (x_{0}) - \underset{S_{A} + S_{B}}{\int \int} \frac{\partial G (x, x_{0})}{\partial n} ϕ (x) d s = \\ - \underset{S_{A} + S_{B}}{\int \int} \frac{\partial ϕ (x)}{\partial n} G (x, x_{0}) d s (3) \end{array}$ $\begin{array}{l} α ϕ (x_{0}) - \underset{S_{A} + S_{B}}{\int \int} \frac{\partial G (x, x_{0})}{\partial n} ϕ (x) d s = \\ - \underset{S_{A} + S_{B}}{\int \int} \frac{\partial ϕ (x)}{\partial n} G (x, x_{0}) d s (3) \end{array}$

积分方程式 (3) 虽然应用简单, 但固体角α随着x₀的位置不同有不连续的值, 当x→x₀时, 格林函数及其空间导数还存在奇异性, 其直接积分很难得到精确值。采用Teng和Eatock Taylor^[10] 的方法, 对于漂浮物体在内域得到另一个积分方程

$(1 - α) ϕ (x_{0}) + \underset{S_{A} + S_{B}}{\int \int} \frac{\partial G_{0} (x, x_{0})}{\partial n} ϕ (x_{0}) d s = 0 (4)$ $(1 - α) ϕ (x_{0}) + \underset{S_{A} + S_{B}}{\int \int} \frac{\partial G_{0} (x, x_{0})}{\partial n} ϕ (x_{0}) d s = 0 (4)$

其中G₀=- (1/r+1/r₁) /4π, r₁=[R²+ (z+z₀) ²]^1/2。

将式 (3) 和式 (4) 相加, 得一新积分方程

$\begin{array}{l} ϕ (x_{0}) - \underset{S_{A} + S_{B}}{\int \int} [\frac{\partial G (x, x_{0})}{\partial n} ϕ (x) - \\ \frac{\partial G_{0} (x, x_{0})}{\partial n} ϕ (x_{0})] d s = - \underset{S_{A} + S_{B}}{\int \int} \frac{\partial ϕ (x)}{\partial n} G (x, x_{0}) d s (5) \end{array}$ $\begin{array}{l} ϕ (x_{0}) - \underset{S_{A} + S_{B}}{\int \int} [\frac{\partial G (x, x_{0})}{\partial n} ϕ (x) - \\ \frac{\partial G_{0} (x, x_{0})}{\partial n} ϕ (x_{0})] d s = - \underset{S_{A} + S_{B}}{\int \int} \frac{\partial ϕ (x)}{\partial n} G (x, x_{0}) d s (5) \end{array}$

方程式 (5) 中不存在固体角α, 所以不论源点在流体中、物面上或物体内部, 积分方程都是一致的。另外, 当场点与源点重合时, 物面上格林函数空间导数的奇异核可自动抵消掉, 可直接应用高斯积分公式求解。

《3 绕射势和辐射势》

3 绕射势和辐射势

在规则波作用下速度势ϕ可写成

$ϕ (x, t) = Re ϕ (x) e^{i ω t} ‚ (6)$ $ϕ (x, t) = Re ϕ (x) e^{i ω t} ‚ (6)$

复速度势ϕ可分解为入射势ϕ_I、绕射势ϕ_D和辐射势ϕ_R:

$ϕ = ϕ_{Ι} + ϕ_{D} + ϕ_{R} = ϕ_{Ι} + ϕ_{D} + \sum_{j = 1}^{12} - i ω ξ_{j} ϕ_{j} (7)$ $ϕ = ϕ_{Ι} + ϕ_{D} + ϕ_{R} = ϕ_{Ι} + ϕ_{D} + \sum_{j = 1}^{12} - i ω ξ_{j} ϕ_{j} (7)$

其中ϕ_j当j=1, …, 6时为A物体单位运动产生的辐射势, j=7, …, 12时为B物体单位运动产生的辐射势, ξ_j当j=1, …, 6时为A物体运动振幅, j =7, …, 12时为B物体运动振幅。当速度势满足边界条件时, A, B物体表面应用物面条件为

$\begin{array}{l} \frac{\partial ϕ_{D}}{\partial n} = - \frac{\partial ϕ_{Ι}}{\partial n} (8) \\ \frac{\partial ϕ_{j}}{\partial n} = {\begin{cases} [n_{j}^{A} 0], j = 1, 2, \dots, 6, \\ [0 n_{j - 6}^{B}], j = 7, 8, \dots, 12 \end{cases} (9) \end{array}$ $\begin{array}{l} \frac{\partial ϕ_{D}}{\partial n} = - \frac{\partial ϕ_{Ι}}{\partial n} (8) \\ \frac{\partial ϕ_{j}}{\partial n} = {\begin{cases} [n_{j}^{A} 0], j = 1, 2, \dots, 6, \\ [0 n_{j - 6}^{B}], j = 7, 8, \dots, 12 \end{cases} (9) \end{array}$

由式 (5) 、式 (8) 和式 (9) 可求出绕射势和辐射势。辐射势产生附加质量和辐射阻尼, 入射势和绕射势产生激振力。

《4 系统的运动响应》

4 系统的运动响应

物体的运动响应幅值需通过刚体运动方程确定:

$- ω^{2} Μ ξ - i ω B ξ + Κ ξ = f + f_{m} + f_{e} (10)$ $- ω^{2} Μ ξ - i ω B ξ + Κ ξ = f + f_{m} + f_{e} (10)$

式中M为物体的质量矩阵, B为物体的阻尼矩阵, K为系泊系统的刚度矩阵, f为流体作用力, f_m为物体的重力部分, 在Z方向上的分量为-Mgn₃, M为物体的质量, 其他分量为零, f_e为来自外部系泊系统的静力部分。流体作用力可通过物体湿表面上的流体压强积分求得。考虑到静水压力、重力、外部静系泊力作用下物体处于静止状态, 式 (10) 可改写为

$\begin{array}{l} (- ω^{2} (Μ + a) - i ω (B + b) + (Κ + C)) ξ = \\ f_{e x} + f_{e} (11) \end{array}$ $\begin{array}{l} (- ω^{2} (Μ + a) - i ω (B + b) + (Κ + C)) ξ = \\ f_{e x} + f_{e} (11) \end{array}$

其中f_ex为激振力, C为恢复力矩阵, a为附加质量矩阵, b为辐射阻尼矩阵。忽略系统的阻尼阵 (即B = 0) 、浮体不受到外部约束的束缚 (即K=0) , A, B两物体分别满足的运动方程为

$\begin{array}{l} (- ω^{2} (Μ_{A} + a_{A A}) - i ω b_{A A} + C_{A}) ξ_{A} + \\ (- ω^{2} a_{A B} - i ω b_{A B}) ξ_{B} = f_{e x A} + F_{L} (12) \\ (- ω^{2} (a_{B A} - i ω b_{B A}) ξ_{A} + (- ω^{2} (Μ_{B} + a_{B B}) - \\ i ω b_{B B} + C_{B}) ξ_{B} = f_{e x B} - F_{L} (13) \end{array}$ $\begin{array}{l} (- ω^{2} (Μ_{A} + a_{A A}) - i ω b_{A A} + C_{A}) ξ_{A} + \\ (- ω^{2} a_{A B} - i ω b_{A B}) ξ_{B} = f_{e x A} + F_{L} (12) \\ (- ω^{2} (a_{B A} - i ω b_{B A}) ξ_{A} + (- ω^{2} (Μ_{B} + a_{B B}) - \\ i ω b_{B B} + C_{B}) ξ_{B} = f_{e x B} - F_{L} (13) \end{array}$

其中f_exA, f_exB分别是物体A和B上受到的波浪力和力矩, M_A, M_B分别是物体A和B的质量矩阵, C_A, C_B分别是物体A和B的恢复力矩阵, a_AA, b_AA是物体A运动时物体A的附加质量和辐射阻尼, a_BB, b_BB是物体B运动时物体B的附加质量和辐射阻尼, a_AB, b_AB是物体A运动时对物体B产生的附加质量和辐射阻尼, a_BA, b_BA是物体B运动时对物体A产生的附加质量和辐射阻尼 (2个物体水动力的相互影响主要体现在附加质量和辐射阻尼上) , F_L是两物体间联系对物体产生的作用力和力矩。两物体所受的约束力和约束力矩大小相等方向相反, 不同的连接形式F_L的表达式不同, 对于铰连接或滑槽连接, 如果不能限制物体某一方向的运动, 则该项约束力或力矩就为零, 对于柔性的弹簧连接, F_L等于弹簧刚度矩阵与物体位移的乘积。

以刚性铰连接的两物体 (见图1) 为例。对于这两物体只有绕Y轴的相对自由转动, 对应地铰连接的约束力分量为

$F_{L} = (F_{L 1}, F_{L 2}, F_{L 3}, F_{L 4}, 0, F_{L 6})^{Τ} (14)$ $F_{L} = (F_{L 1}, F_{L 2}, F_{L 3}, F_{L 4}, 0, F_{L 6})^{Τ} (14)$

这样, 式 (12) 和式 (13) 中有17个未知数, 而方程数仅有12个。

考虑到铰连接处的位移连续条件, 通过2个局部坐标系分别求得连接点处位移和转角的方程为,

$\begin{array}{l} x_{L A} + ε [ξ_{A} + α_{A} \times (x_{L A} - x_{0 A})] = \\ x_{L B} + ε [ξ_{B} + α_{B} \times (x_{L B} - x_{0 B}], \\ α_{A x} = α_{B x}, α_{A z} = α_{B z} (15) \end{array}$ $\begin{array}{l} x_{L A} + ε [ξ_{A} + α_{A} \times (x_{L A} - x_{0 A})] = \\ x_{L B} + ε [ξ_{B} + α_{B} \times (x_{L B} - x_{0 B}], \\ α_{A x} = α_{B x}, α_{A z} = α_{B z} (15) \end{array}$

其中x_LA, x_LB是连接点分别在2个局部坐标中的坐标值, x_OA, x_OB分别是2个物体的转动中心在局部坐标中的坐标值, ξ_A, ξ_B是2个物体的平动位移, α_A, α_B是两物体的转动角位移, α_Ax, α_Bx, α_Az, α_Bz分别是A, B两物体角位移在X和Z方向上的分量。

式 (12) 、式 (13) 和式 (15) 共有17个未知量, 17个线性方程, 因此可求解两物体的运动响应和铰接约束力。如果物体间没有连接则由式 (12) 和式 (13) 即可求出物体的运动响应。

《5 数值分析》

5 数值分析

《5.1刚性连接》

5.1刚性连接

采用和Newman相同的算例, 在无限水深的情况下, 波浪入射角与X轴正向夹角为0°, 采用无因次化的方程计算。取2个相同的方箱组成的系统, 每个方箱长40 m, 宽10 m, 高10 m, 吃水深5 m, 质量均匀分布, 两方箱有绕Y轴的相对转动, 间距10 m, 如图3所示, 在每个方箱表面划分单元, 求解积分方程时采用高阶边界元方法, 为了保证方法的通用性, 不利用结构的几何对称简化。为了验证数值方法的收敛性, 划分了2种网格, 第一种为8×4×2个单元, 2个方箱共160个单元, 第二种划分为24×12×6个单元, 在垂向上为余弦网格, 2个方箱共1 400个单元。 Newman采用WAMIT计算, 每个方箱长、宽和水深方向划分32×16×8个单元, 2个方箱共2 560个单元, 利用结构的几何对称简化, 实际计算中仅在1/4物面上划分单元。

《图3》

图3铰连接方箱示意图

Fig.3 Sketch of the hinged barges

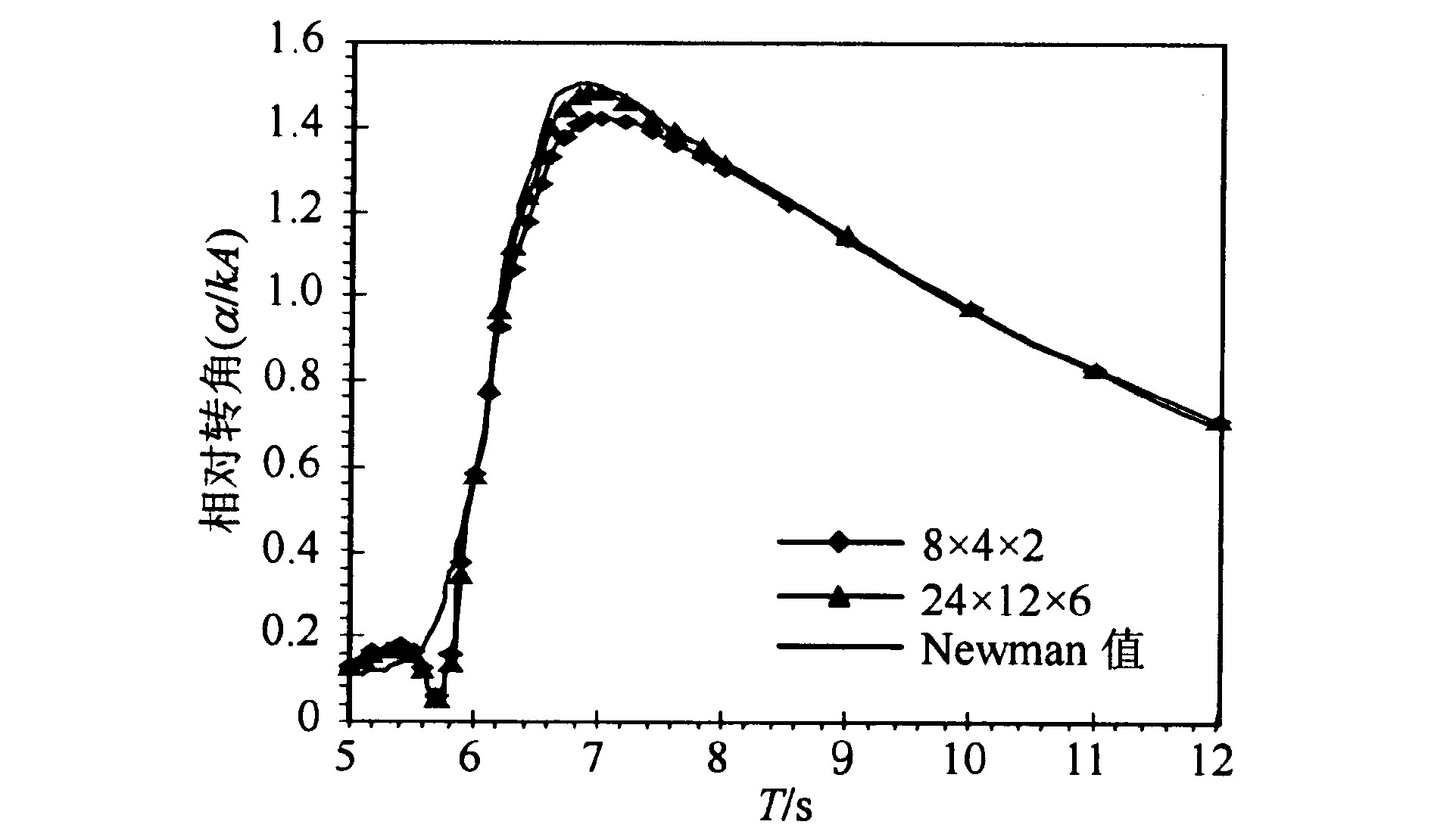
通过数值计算, 对2个方箱的相对转角和2个方箱在连接点处的升沉位移与Newman的结果进行了比较。图4纵坐标为2个方箱的相对转角, 它除以波陡kA使无因次化, T为周期, 图5纵坐标为两方箱连接点处的升沉位移, 它除以入射波幅A使无因次化。从图4和图5中可看出, 在低频部分的结果与Newman结果符合得很好, 随着单元划分数量的增加, 在高频部分曲线最高值逐渐逼近Newman的结果, 但是高频部分周期在5～6.2 s之间有一个波动, Newman的值则平滑上升, 增加单元划分数量后波动仍未消除。

《图4》

图4两个方箱的相对转角

Fig.4 Relative angular deflection

计算系统中2个方箱绕Y轴相对转动的自振频率, 公式为

$| - ω^{2} (Μ_{7 \times 7} + a_{7 \times 7}) + C_{7 \times 7} | = 0 (16)$ $| - ω^{2} (Μ_{7 \times 7} + a_{7 \times 7}) + C_{7 \times 7} | = 0 (16)$

式 (16) 中, 把系统作为一个整体, 共有7个自由度, 包括两物体刚性连接时的6个自由度和两物体相对转动的一个自由度。M_7×7为物体的质量矩阵, C_7×7为恢复力矩阵, a_7×7为相应入射周期的附加质量矩阵, 式 (16) 中忽略了附加阻尼的影响。由式 (16) 得出:当入射周期在5～6.2 s之间变化时, 自振角频率在1.0532～1.0545 s^-1之间变化, 对应的自振周期在5.9584～5.9658 s之间变化, 因此可得出, 图4和图5中的波动是由于入射波的周期与物体的自振周期接近而导致的。

《图5》

图5连接点处的升沉位移

Fig.5 Heave amplitude at the hinged joint

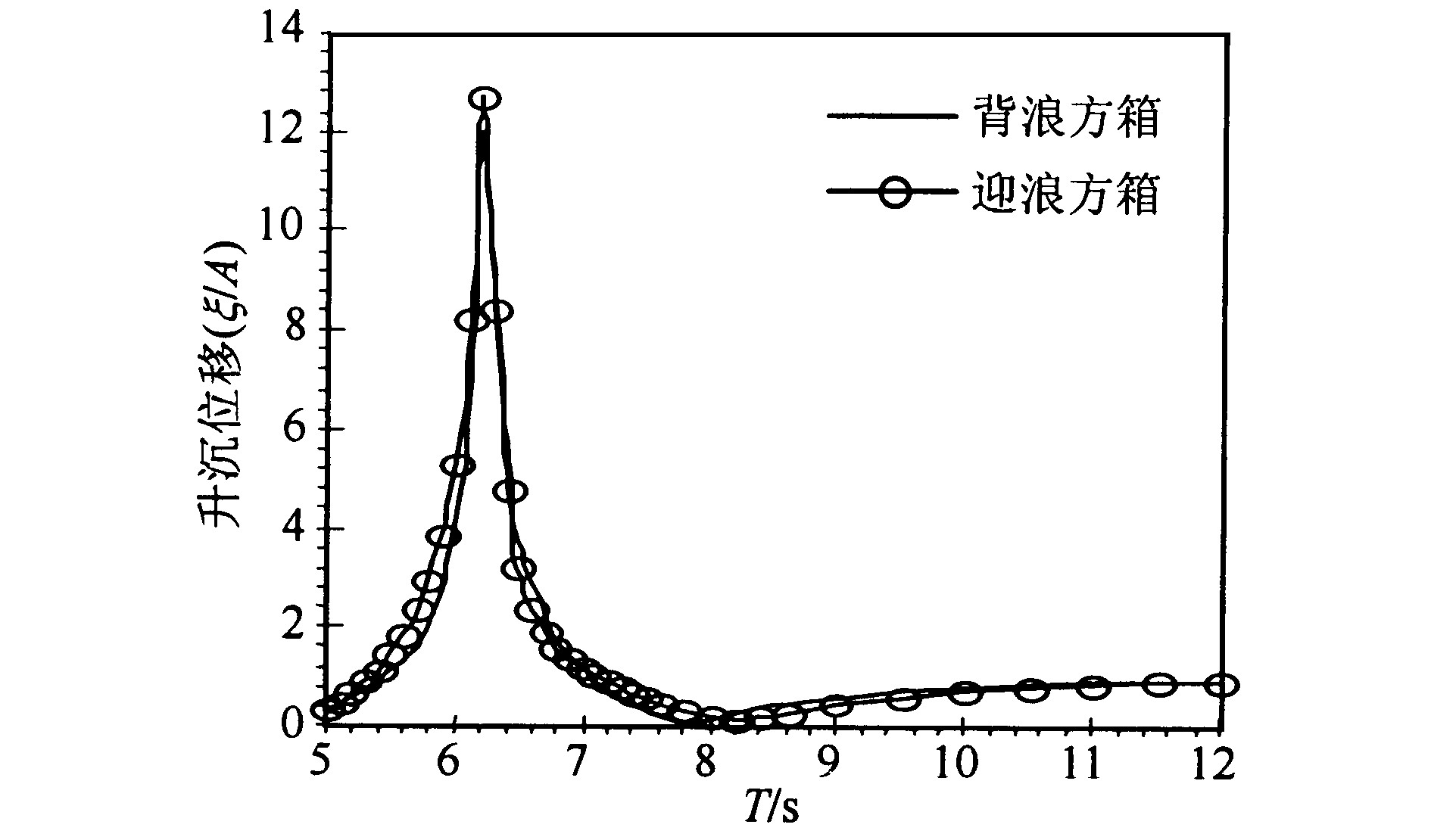
取单元划分为24×12×6的网格, 对于波浪的入射方向而言把两方箱分为迎浪方箱和背浪方箱。从图6和图7可看出, 两方箱无论是迎浪还是背浪, 它们的纵摇转角和升沉位移都相差不大, 但是相位角不同。

《图6》

图6两方箱纵摇角位移

Fig.6 Angular deflections of two barges

《图7》

图7两方箱升沉位移

Fig.7 Heave amplitudes of two barges

《5.2柔性连接》

5.2柔性连接

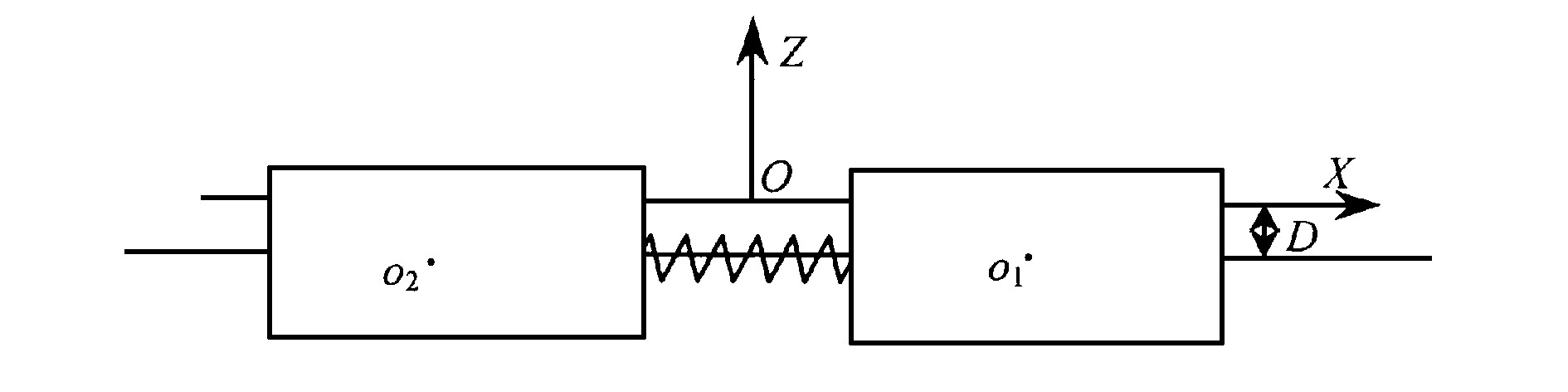
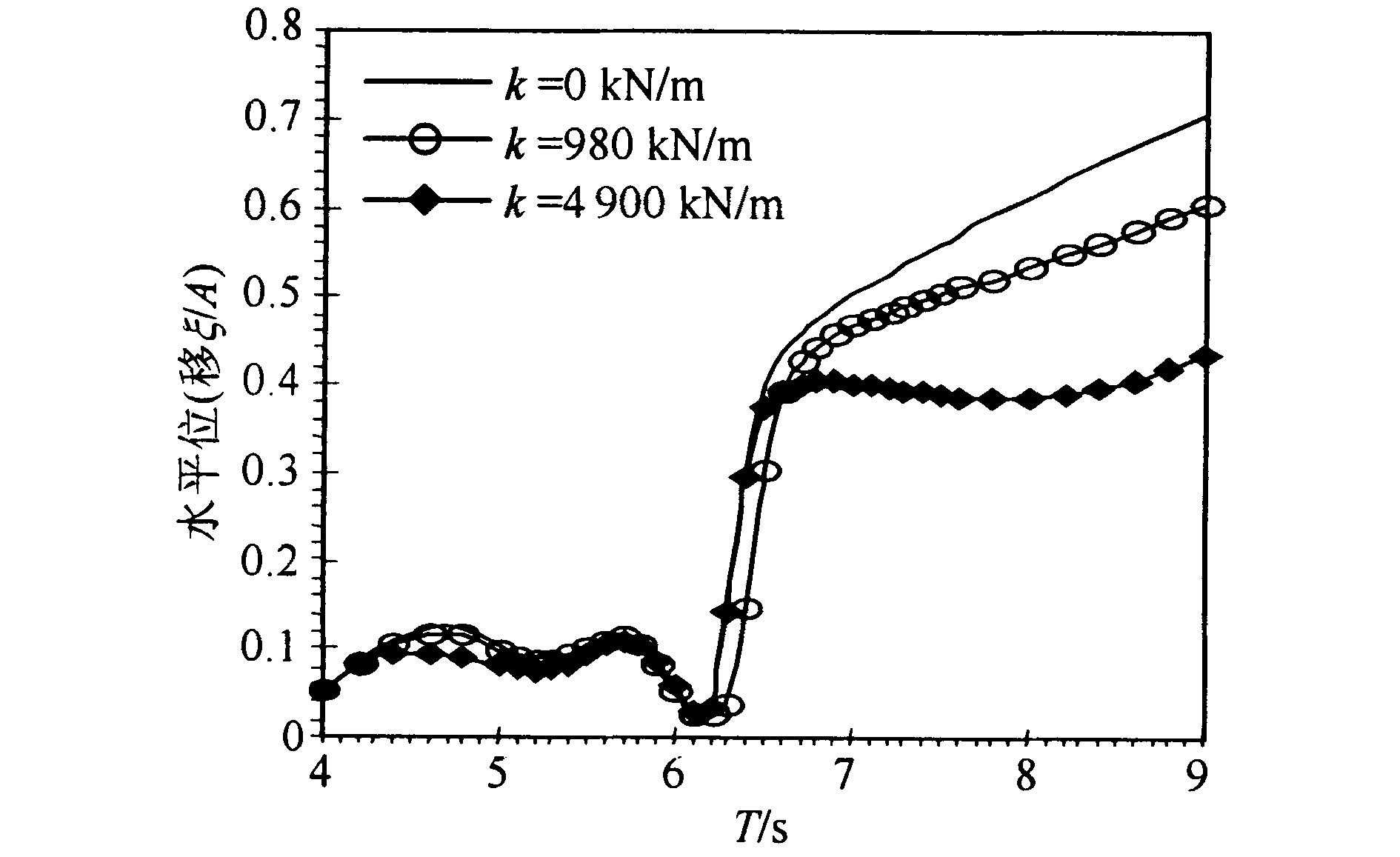
物体间采用弹簧连接, 如图8所示, 弹簧刚度K, D为弹簧连接点与物体转动中心的垂向距离。采用同上例相同的两个方箱, 单元划分为8×4×2, 方箱间采用弹簧连接, 弹簧刚度K分别取0, 980 kN/m, 4900 kN/m, 此例中D为零, 所以弹簧的影响主要体现在对水平位移产生的影响, 结果中比较了两个方箱的水平位移、纵摇角位移及弹簧力。

《图8》

图8弹簧连接方箱示意图

Fig.8 Sketch of two barges connected with spring floating on water

计算中弹簧的刚度矩阵取^[5]

$c = [\begin{matrix} Κ & 0 & 0 & 0 & Κ D & 0 & - Κ & 0 & 0 & 0 & - Κ D & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ Κ D & 0 & 0 & 0 & Κ D^{2} & 0 & - Κ D & 0 & 0 & 0 & - Κ D^{2} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}] (17)$ $c = [\begin{matrix} Κ & 0 & 0 & 0 & Κ D & 0 & - Κ & 0 & 0 & 0 & - Κ D & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ Κ D & 0 & 0 & 0 & Κ D^{2} & 0 & - Κ D & 0 & 0 & 0 & - Κ D^{2} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}] (17)$

则每个方箱受到的连接约束力为

$F_{L 6 \times 1} = c_{6 \times 12} ξ_{12 \times 1} 。$ $F_{L 6 \times 1} = c_{6 \times 12} ξ_{12 \times 1} 。$

从图9和图10中可看出在一定范围内弹簧刚度对水平位移的影响很小, 只有当弹簧的刚度很大时才在低频部分对水平位移产生明显的影响。因为此例中物体尺度较大, 弹簧对物体产生的作用力与物体受到的激振力相比很小, 在一定范围内可忽略弹簧对水平运动的影响。

《图9》

图9背浪方箱的水平位移

Fig.9 Sway response of the leeside barge

《图10》

图10迎浪方箱的水平位移

Fig.10 Sway response of the weather side barge

图11和图12分别为背浪方箱和迎浪方箱的纵摇角位移比较。弹簧连接点与物体转动中心的垂向距离为零, 因此弹簧对纵摇运动的影响很小, 从图中也可看出只有当周期较大时纵摇角位移才有很小的变化。图13为不同弹簧刚度时弹簧的受力图, 纵坐标为弹簧力, 它除以ρgabA使无因次化, a, b分别为方箱的长和宽。

《图11》

图11背浪方箱纵摇角位移

Fig.11 Pitch deflection of the leeside barge

《图12》

图12迎浪方箱纵摇角位移

Fig.12 Pitch deflection of the weather side barge

《图13》

图13弹簧受力

Fig.13 Tensile force of the spring

《6 结语》

6 结语

应用边界积分方程方法建立了波浪与两相连浮体相互作用的分析方法, 该方法考虑了物体间的水动力干涉问题, 物体运动量通过各物体的运动方程和之间联系的约束条件确定。用该方法对2个铰链接和弹簧连接的漂浮方箱做了计算, 结果表明:

1) 通过有效地选取积分范围, 计算波浪与单物体相互作用的边界积分方法可用于解决波浪与2个任意形式相连物体的相互作用上, 这一方法可推广到波浪与多个相连物体的相互作用中。

2) 对于波浪与两铰连接漂浮方箱组成系统, 在低频处的结果与Newman结果吻合良好, 随着频率的增加, 为得到收敛的结果需要更多单元。在方箱关于铰转动的自振频率处, 计算的铰接点处转角和垂向位移发生快速变化, 而Newman未提到这一现象。

3) 在一般频率下, 铰接处的垂向位移和方箱关于铰的转角不是很大, 但在方箱铰转动的自振频率处, 铰接处的垂向位移和方箱关于铰的转角迅速增大。

4) 对于弹簧相连的2个方箱, 当弹簧刚度较小时弹簧刚度对方箱水平位移的影响很小。随着弹簧刚度的增大, 低频区域对方箱水平位移产生明显的影响。

Show More