浅水动力模型应用实例有河道流量及洪水预报、洪水漫滩、近海风暴潮、溃坝决堤等，因此有关浅水波方程的求解近年来备受关注。有限体积法[1]是将计算区域划分为一系列不重复控制体，将待解的微分方程对每一个控制体进行积分。有限体积法的离散格式有很多种，其各自的区别主要是节点布置以及对控制体流出通量的计算方法不同。单元节点布置于网格节点上，尝试用有限差分法计算界面上的通量，使得差分法到达二阶精度。通过实例计算，比较一阶精度和二阶精度的差别，并验证该方法的适应性。

《1　数学模型》

1　数学模型

二维浅水波控制方程[2]的分量形式为

U = hu，V = hv，u，vU = hu，V = hv，u，v 分别是 x，y 方向的水速，h 是水深，υ 是运动黏滞系数，g 是重力加速度，（ Sox，Soy ）为河道的倾斜效应项，x，y 下标也是求导的意思，（S fx，S fy）为 x，y 方向摩阻底坡。

二维浅水波方程是一个对流 - 扩散方程，可以写成以下形式

上标 I，II 表示导数的阶数，方程式（）至式（1 c）的边界条件是常用的浅水波的边界条件。

《2　数值方法》

2　数值方法

采用有限体积法对方程式（1）进行离散求解，为了适应复杂几何形状流场的数值计算，网格采用任意三角形，节点为网格顶点。使用有限体积法时，把控制体的厚度看成是 1，可得

F 包含对流项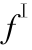（）和黏性扩散项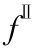（），S 为源项。

《2.1　时间离散》

2.1　时间离散

采用显式离散的方法，则速度对时间的偏导数可以离散成

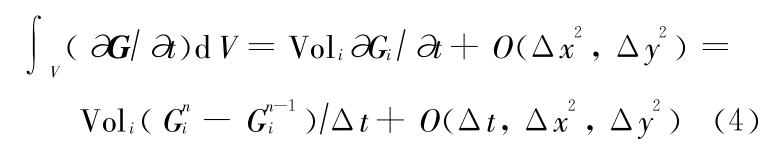
式中，Vol 是控制体的体积，下标 i  表示控制体单元号，G = （ U，V，h）。

《2.2　对流项离散》

2.2　对流项离散

对对流项进行离散，关键是计算控制体表面上的数值通量。在不同的离散格式中，差别最大的是对流项的处理。求控制体表面上的数值通量（对流项控制体如图 1 虚线包含的范围） 采用如下方法

《图1》

图1　对流项控制体

Fig.1　Control volume of convection term

式中，Δ yc1c2 = yc2 - yc1，Δ xc1c2 = xc2 - xc1。积分沿控制体边界逆时针方向，界面上的物理量等于界面上风侧节点上的值，即 fluxc1c2 ＞ 0 时，U c1c2 = Uv1 ；fluxc1c2 ＜ 0 时，Uc1c2 = Uv2。因此，一阶迎风的对流项可以写成通式

为构造一种二阶精度的迎风格式，首先把界面上的数值通量分解成正、负通量之和，得

式中，F += （fluxc1c2 + ｜fluxc1c2 ｜）/2，F – = （｜fluxc1c2 ｜– fluxc1c2）/2。可以看出，对流项的精度与界面上物理量的选取密切相关，例如，对一阶迎风格式，界面上的物理量 U 等于上风侧节点的值 ；对于中心差分格式，界面上 U 值等于界面两边节点上物理量的均值，中心差分格式的精度为二阶，但是不稳定。为了保证格式的迎风特性和格式的精度，在界面上对 U 作 Taylor 展开，可以得到

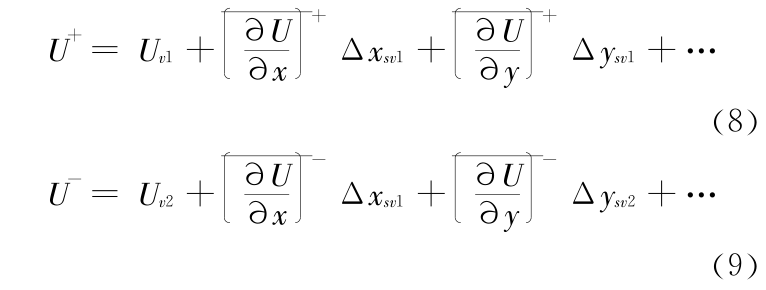
式中，Δ xsv1 = xs - xv1，Δ ysv1 = ys - yv1，Δ xsv2 = xs -xv2，Δ ysv2 = ys - yv2，（ xs，ys ）为界面中心点坐标。式（8）和式（9）中的梯度的选取为一侧梯度与两侧梯度的算术平均中的绝对值较小者，这种方法引入 NND 格式的优点。梯度项的公式的具体计算为

式中，函数 min mod 的定义为

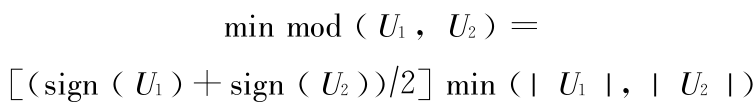
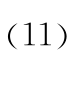
式中，U1 和 U2 是任意的两个变量。

考虑了一阶梯度项的影响，因此，此式的计算精度为二阶精度。将式（7）、式（8）、式（9）和式（10）代入对流项中，可得到二阶迎风的对流项计算公式

《2.3　粘性扩散项》

2.3　粘性扩散项

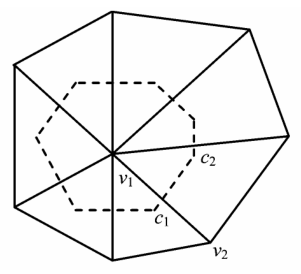
在非结构网格中扩散项的离散要比正交的结构化网格中复杂得多。对单元 v1 作扩散项离散的目的在于，获得能表示 v1 点受其邻点的扩散作用影响的代数关系式。为了计算扩散项中的速度偏导数，引入辅助控制体 v1，c1，v2，c2 （见图 2），并且假设在这控制体上速度的偏导数不变，即可以得到

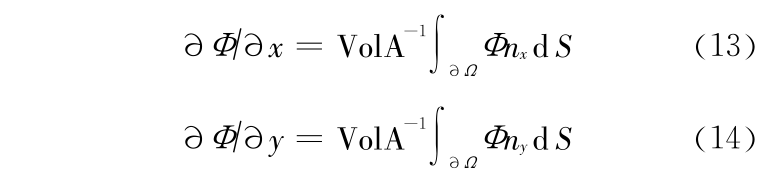
式中，VolA 是辅助控制体的体积，Φ = （ U，V）。

对于平面二维问题，可以得到

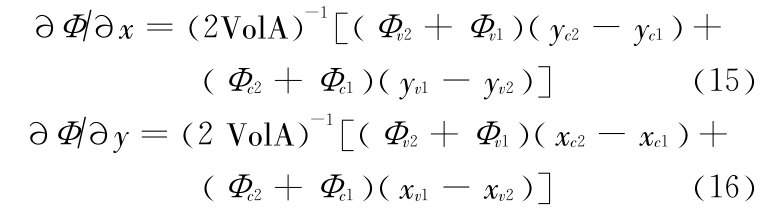
《图2》

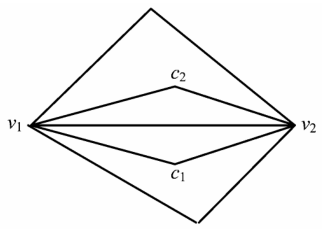
图2　辅助控制方程体积

Fig.2　Auxiliarycontrol volume

把式（4）、式（6）、式（15）和式（16）代入二维浅水波方程式（1），可以得到连续性方程为

ie 表示非结构网格的边数。

对流项为一阶的形式为

式中，

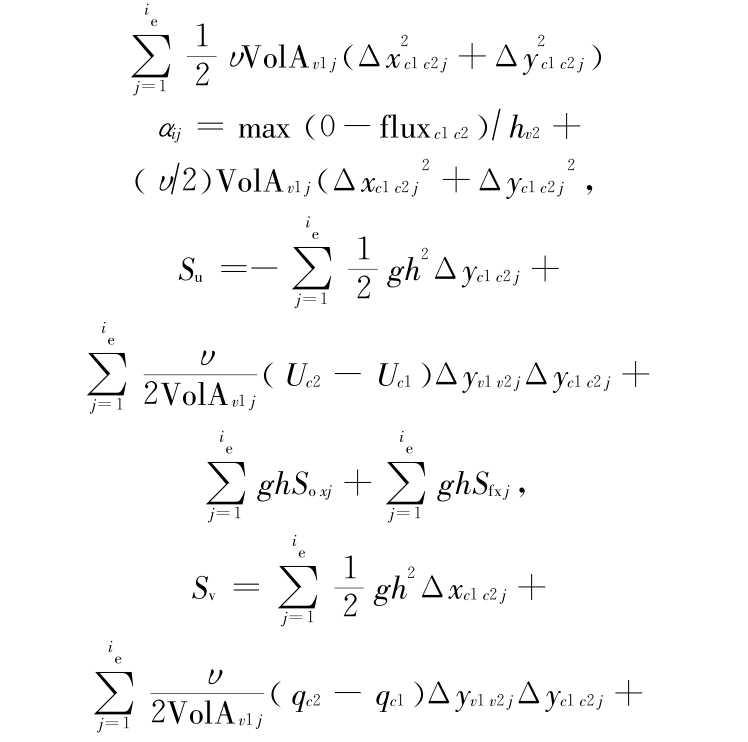
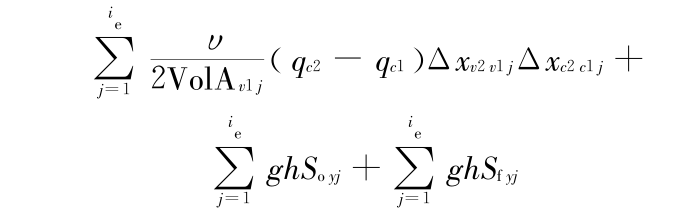
把式（12）、式（14）和式（15） 代入二维浅水方程式（1b）、式（1c）整理后得到对流项为二阶的形式

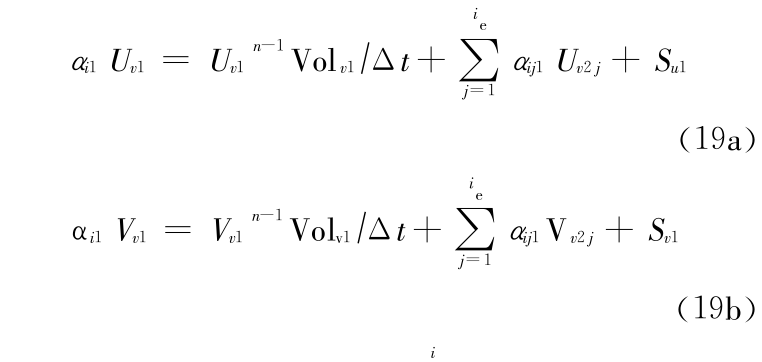
式中

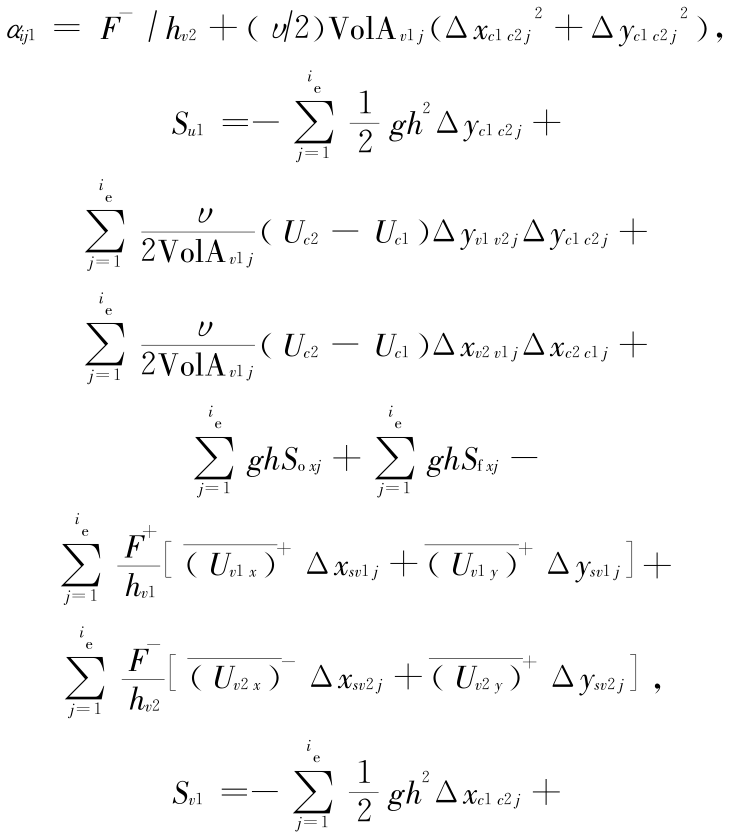
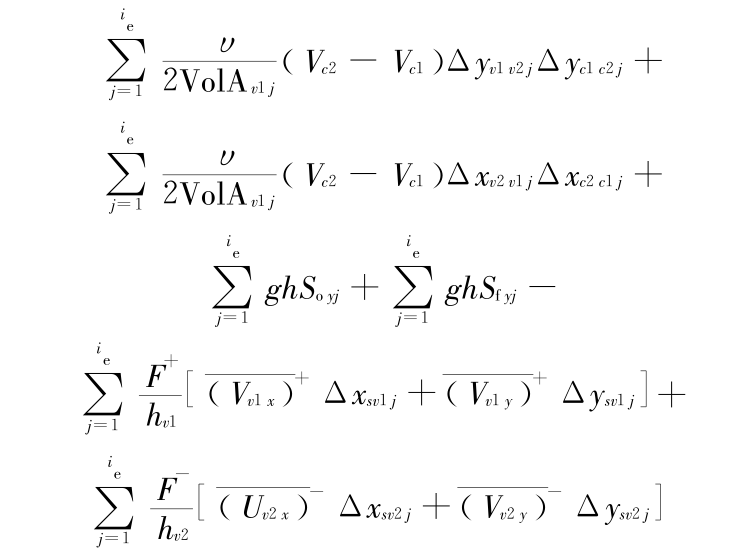
式（18）和式（19）就是建立的一阶、二阶离散格式。对流项的离散采用一阶迎风格式所得到的算法式称为一阶算法。相应地，对流项采用二阶迎风格式离散的算法式称为二阶算法。

《3　计算实例》

3　计算实例

《3.1　二维弯道流动》

3.1　二维弯道流动

弯曲渠道流场的数值模拟计算在许多流体力学研究课题中都作为模型验证实例之一。Rozovskii 于1957 年在一个弯曲弧度为 180° 的底面无坡度的明渠（见图 3）中做了一个实验，测量了水面高度的变化。明渠内岸半径为 0.4 m，外岸半径为 1.2 m。上游到弯管进口的长度为 0.4 m，下游到弯管出口的长度为 1.8 m。渠道截面为矩形。

《图3》

图3　几何尺寸（mm）

Fig.3　Physical dimension

边界条件与实验设为一致，初始进口水面高度为 0.06 m，出口水面高度为 0.057 5 m。进口速度只有沿 x 方向，y 和 z 方向速度为零。沿明渠深度方向速度按 1/7 率变化，水面上在渠道边壁处速度为 0.274 m/s，中心线上速度为 0.297 m/s。图 4 为计算网格。

《图4》

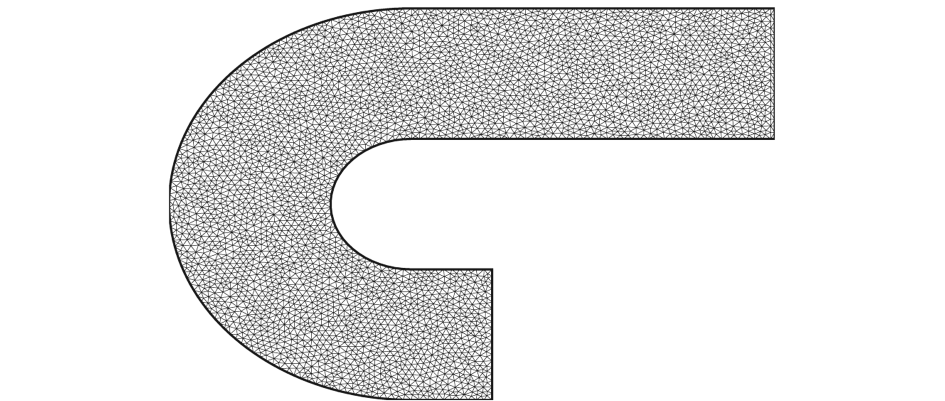
图4　计算网格

Fig.4　Graticule

从图 5 至图 8 和图 9 至图 12 可以看出，一阶算法和二阶算法计算得到的流速场总的趋势是一样的。并且得出这样的结论 ：在顺直进口段，纵向垂线平均流速沿河宽呈对称形分布，入弯后凸岸流速稍增而凹岸流速稍减 ；至某一部位后，又出现相反的调整，流速分布趋于均匀，随之最大垂线平均流速，又显现渐渐移向凹岸 ；出弯后的水流，在一段距离内，靠近外侧河岸的流速大一点。考虑的边界条件是具有粘性的，也就是固壁上的速度为零，这样最大速度不在固壁上。从这些现象来看，总趋势符合弯道的流态。

《图5》

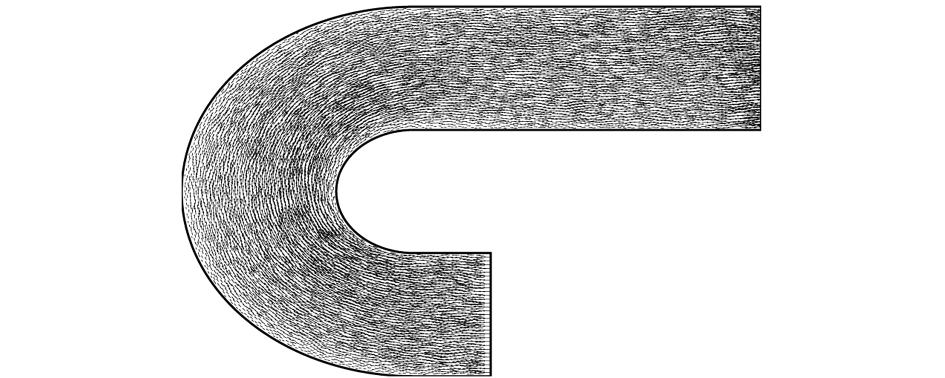
图5　用一阶算法的弯道流速场图

Fig.5　Velocity field of curved conduit by the first-order calculation

《图6》

图6　用一阶算法的弯道典型断面流速图

Fig.6　Typical cross-section velocity of curved conduit by the first-order calculation

《图7》

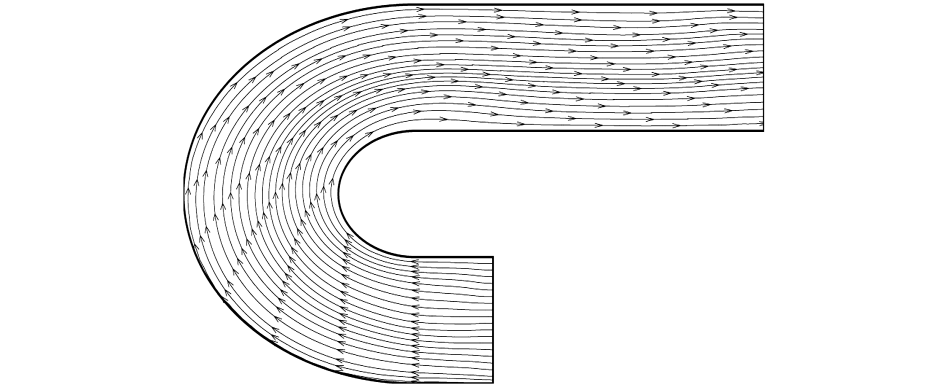
图7　用一阶算法的弯道流线图

Fig.7　Streamline of curved conduit by the first-order calculation

《图8》

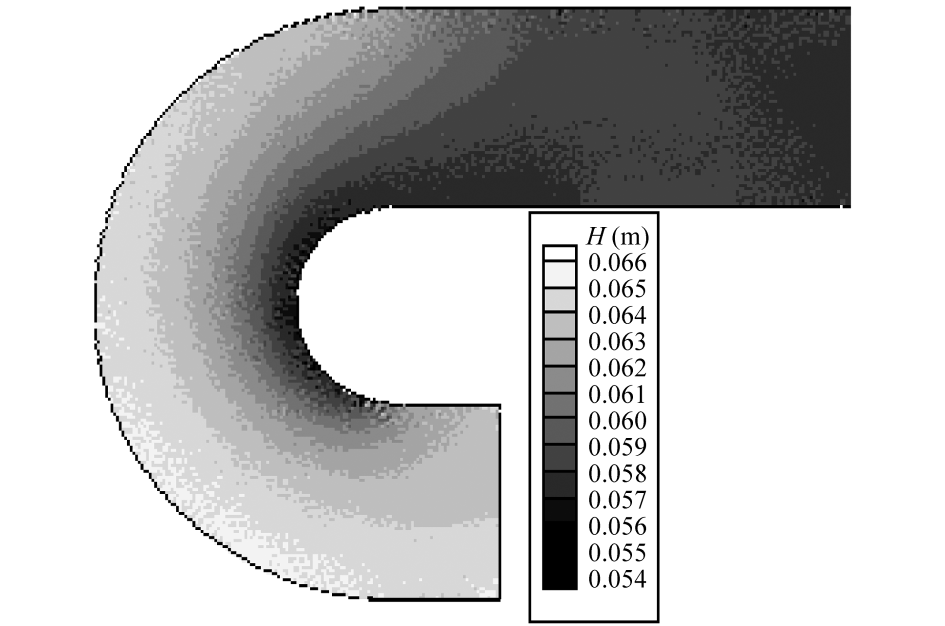
图8　用一阶算法的弯道水位 H 等势图

Fig.8　Potential line of curved conduit by the first-order calculation

《图9》

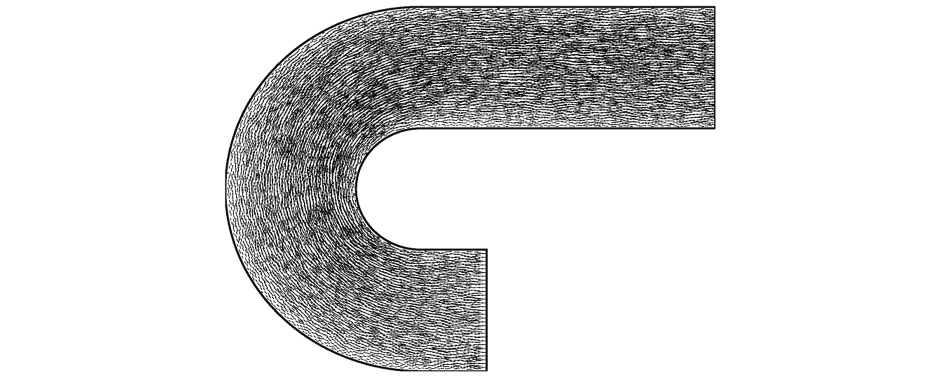
图9　用二阶算法的弯道流场图

Fig.9　Velocity field of curved conduit by the second-order calculation

《图10》

图10　用二阶算法的弯道典型断面流速图

Fig.10　Typical cross-section velocity of curved conduit by the second-order calculation

《图11》

图11　用二阶算法的弯道流线图

Fig.11　Streamline of curved conduit by the second-order calculation

《图12》

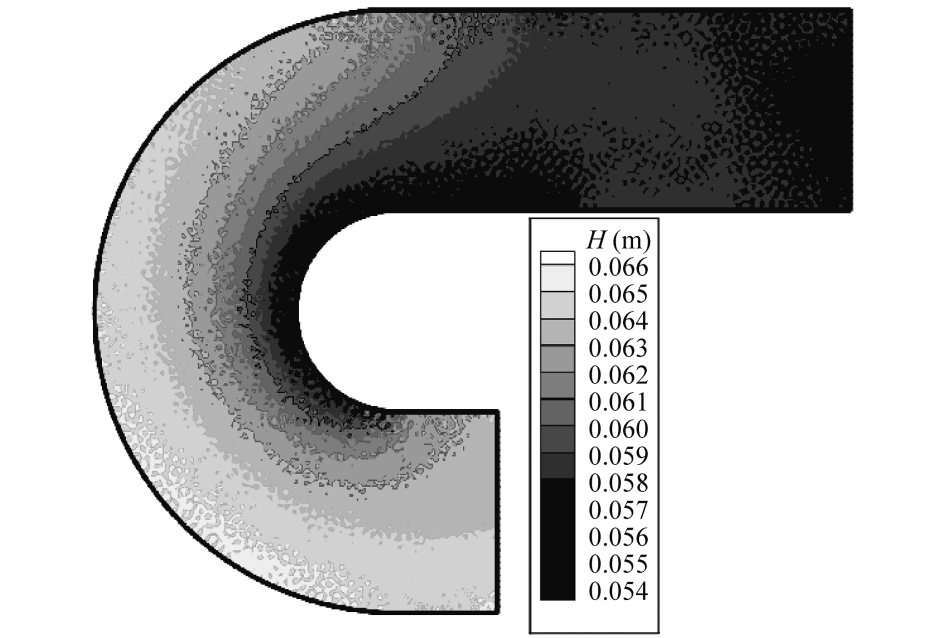
图12　用二阶算法的弯道水位 H 等势图

Fig.12　Potential line of curved conduit by the second-order calculation

图 13 为模型的计算值、Leschziner 的计算值与 Rozovskii 的实验值中明渠内岸、外岸水面超高比较。图中横坐标为明渠弯道的角度（θ ），纵坐标为水面超高，即 η = [ ( 水面高度 - 0.06) / 0.06 ] × 100 %。笔者进行平面二维的模拟计算，对上面的有限体积法进行验证。一阶算法计算结果和实验值比较最大的误差为 8 % ；二阶算法计算结果和实验值相比的最大误差只有 3.5 %。而且从变化趋势来看，一阶算法计算结果和二阶算法计算结果都比较符合水位的变化趋势。但是二阶算法计算结果，更接近实验值。

《图13》

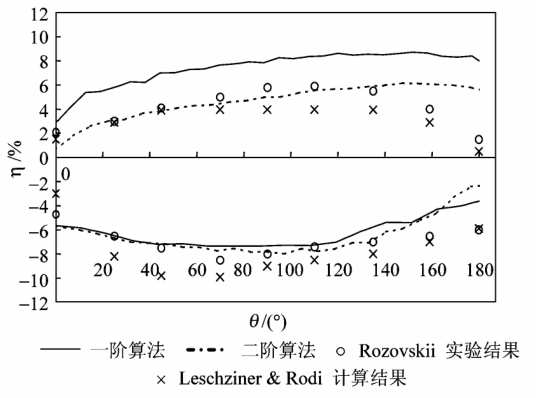
图13　计算值与实验值中明渠内岸、外岸水面超高比较

Fig.13　The comparison of the calculated results and experimental results

采用一阶、二阶有限体积法的离散格式，能较好地模拟出弯道的流场。从弯道的水位看，二阶算法比一阶算法的结果好一点。从图 8 上可以看出，一阶算法计算得到的水位会出现微小的锯形情况。比较一阶算法和二阶算法计算得到的水位等势图（见图 8 和图 12）可以看出，一阶算法计算得到的等势线明显没有二阶算法计算得到的那么光滑。但是从总的趋势来看，一阶算法和二阶算法计算得到的趋势都符合流体流动的规律。

《3.2　二维溃坝流动》

3.2　二维溃坝流动

实际工程中溃坝大多数出现局部、部分的溃决。在很多国内外的文章[3,4]中，特别是算法验证中，很多人使用部分溃坝来验证。研究的模型尺寸如图 14 所示，坝的中间有 75 m 的溃决口。在国内外很多的文章中，忽略坝的宽度，这样在网格的生成和节点编号时要进行特别处理。为了方便，把坝的宽度定义为 2 m。初始条件为，坝上游的水位为 10 m 坝的下游为 5 m。采用的网格如图 15 所示。网格中一共有 17 647 个点，34 766 个单元。

《图14》

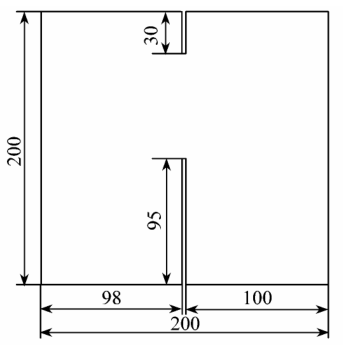
图14　溃坝模型示意和尺寸图（m）

Fig.14　Diagrammatic sketch and dimensional

《图15》

图15　溃坝模型计算的网格

Fig.15　Graticule of dam-break model calculation

图 16 给出的是溃坝 7.2 s 后的水面图，图 16（a） Sergio Fagherazzi 等[5]采用间断 Galerkin 方法计算得到的结果，图 16（b）一阶算法结果，图 16（c）二阶算法结果。从图 16 中可以看出，3 个图都有同样的规律，当坝体瞬间溃决消失后，产生的负波向上游传播，产生的正波向下游传播，波的传播是按弧形前进的，上游两边水向中间流动，水面就形成一个“漏斗”，同时下游的正波也在往下游传播，坝决口在坝下游拐点处产生回流，水波碰到岸边后会产生反射，水面会变得很陡。这些现象均符合水流流态。图17 是 3 种算法的水位等势图。比较图 16 和图 17 可以得到一阶算法、二阶算法计算得到结果和 Sergio Fagherazzi 等人采用间断 Galerkin 方法计算得到的结果很吻合，并且能够很好地捕捉溃坝波的前进的波峰。

《图16》

图16　溃坝后 7.2 s 的水面图

Fig.16　Dam-break’s water level （t = 7.2 s）

《图17》

图17　溃坝后 7.2 s 的水位等势图

Fig.17　Dam-break’s equipotential water level graph （t = 7.2 s）

《4　结语》

4　结语

通过算例可以看出，采用的有限体积法结合有限差分法建立的浅水波模型的一阶、二阶离散格式能很好地模拟二维浅水波方程，方法简单，且计算结果可靠。对于弯道恒定流，一阶和二阶算法都能很好地模拟流速场 ；而对于水位，一阶算法的模拟得到的水面没有二阶算法模拟得到的水面平滑，而且二阶算法结果得到的结果更加接近实验值。对于溃坝问题，有限体积法能很好地保持解在间断处的陡峭，有较高的间断分辨率，同时能对洪水波遇到障碍物的反射波进行捕捉。总之，所介绍的方法能模拟弯道流动和部分溃坝洪水波的演进过程，能很好地模拟出水流运动特性。