《1 前言》

1 前言

在概率论与随机过程的研究中，正态分布的地位举足轻重。正态分布的密度函数和分布函数具有比较简单的数学形式和一些很好的数学性质。正态分布是许多重要概率分布的极限分布，许多非正态的随机变量是正态随机变量的函数，这些都使得正态分布在理论和实际中应用非常广泛。

中心极限定理从理论上阐述了产生正态分布的条件，中心极限定理简单直观的阐述是：如果决定某一随机变量结果的是大量微小的、独立的随机因素之和，并且每一随机因素的单独作用相对均匀的小，没有一种因素可起到压倒一切的主导作用，那么这个随机变量一般近似服从于正态分布。正态分布广泛存在于自然现象、社会现象、科学技术以及生产活动中，在实际中遇到的许多随机现象都服从或者近似服从正态分布。例如，正常生产条件下的产品质量指标，随机测量误差，同一生物群体的某种特征，某地的年平均气温等。

通常在讨论有关概率问题时，分布函数 F（x）起着非常重要的作用，其尾分布函数 1－F（x）在实际中的应用尤为重要。 例如，在有关可靠性的分布中，可靠性与失效率等概念都同尾分布函数有关。 自 20 世纪 60 年代以来，国外出现了大量重尾分布的研究文献[1~3]。但是究竟什么是重尾分布？ 至今仍未有一个确切统一的定义来描述，甚至名称也没有完全统一。不同文献中，重尾分布（heavy-tailed distribution） 也 被称为胖尾( fat-tailed）、 厚尾( thick-tailed）或者长尾（long-tailed )分布。在文章中，笔者把这些名词当作同义词，在不引起混淆的情况下，统称为重尾分布。

重尾分布在分支过程、排队论和可靠性的研究中，特别是近年来在金融工程、数量经济和保险精算等研究领域都有广泛应用。特别是 1998 年 BA 模型的提出[4]，使全世界不同领域的众多学者对幂律分布产生了极大的兴趣和热情。 而幂律分布就是一类重尾分布。由于优胜劣汰的竞争机制在生物界、人类社会等诸多领域中都或多或少地存在，因此，越来越多的研究者倾向于重尾分布具有不亚于正态分布的意义。

无论从产生条件、数学形式还是物理意义而言，重尾分布都和正态分布截然不同。那么，二者之间到底有无内在联系？ 有无转换桥梁？ 这将是以下所要论述的中心问题。

《2 正态分布与重尾分布》

2 正态分布与重尾分布

定义1　若随机变量 X 的概率分布函数形式为：

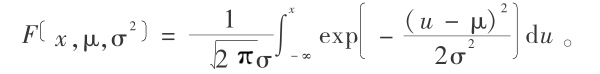
或者概率密度函数为：

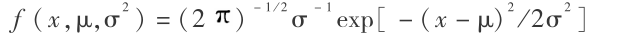
则称 X 为正态分布，记为 X ~ N ( μ，σ2 )。 其中，μ 和 σ2 分别是正态分布的期望和方差，分别表征随机变量的最可能取值以及一切可能取值的离散程度。

重尾分布则有很多等价的数学定义，其中 Em - brechts 的定义应用最为广泛[1]。

定义2　称随机变量 X 是重尾分布，如果它不存在指数阶矩， 即对任意 λ ＞ 0， 有 Ee λX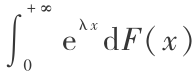＝ =  。其中 F（x）是 X 的分布函数。

还有一种定义是相对于正态分布而言，以四阶中心矩为基础。四阶中心矩具有峰度（kurtosis）的含义，峰度是统计中描述分布状态的一个重要特征值，用以判断概率密度函数曲线相比于正态分布的尖平程度。 如果将正态分布视为常峰态，密度函数曲线的形状比正态分布更高更瘦的称为高峰态，否则称为低峰态。

定义3[5]　随机变量 X 称为是重尾的，如果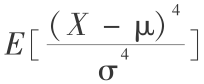  ＞ 3 ，其中 μ 、σ 分别为 X 的期望和标准差。

正态分布的峰度为 3，因此该性质被称为超过或大于峰度。但是，该定义只适用于四阶矩存在的情况。另一种是判断重尾分布较为直观的定义。

定义4[1]　如果密度函数是以幂指数衰减至 0 的，则该分布函数为重尾的；如果密度函数是以指数函数衰减至 0 的，称该分布函数为轻尾的。

形象而言，重尾分布就是密度函数“尾巴”比较长的分布。 在应用领域，它的物理意义可以解释为极端事件的概率不为 0 。如保险业的大额索赔问题，在 N 次索赔中有一次索赔的额度非常大，以至于其他 N －1 次索赔相对于这次索赔而言是微不足道的，这类大额索赔问题就需要用重尾分布来处理。这类问题就是所谓的极端事件问题，如地震、洪水、股灾等。这类问题研究在现实中有很强的应用价值，尤其是“911”事变后，大量保险公司破产，极端事件的研究更成为新的前沿研究热点。因此，重尾分布的研究也受到越来越多学者的关注。

《3 云模型——超熵与重尾分布》

3 云模型——超熵与重尾分布

云模型是利用 3 个数字特征，结合特定算法实现的定性概念及其定量表示之间的转换模型。其 3 个数字特征及具体算法定义如下[6]。

期望 Ex：云滴在论域空间分布的期望，即最能够代表定性概念的点。

熵 En：代表定性概念的粒度，熵越大，概念越宏观。

超熵 He：熵的不确定性度量，即熵的熵。

定义5  设 U 是一论域, C 是 U 上的定性概念，（Ex， En， He）为 C 的数字特征。若定量值 x∈U 是定性概念 C 的一次随机实现，x 满足：

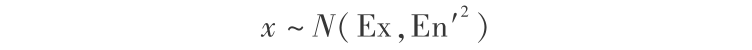
其中，En′ ~ N ( En，He2 )， N ( En， He2）表示期望为 En 、方差为 He2 的正态分布。

x 对 C 的确定度 y 根据下式计算： y = 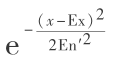，那么 x 在论域 U 上的分布 X 称为正态云。

容易计算，正态云 X 的概率密度函数为 f X (x ) = 。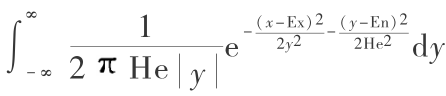

文献[6]已经证明，正态云模型的期望和方差分别为 Ex 和 En2 + He2 。其概率密度函数以 Ex 为中心左右对称。 接下来，我们将证明，正态云 X 还具有重尾特性。

定理 1：当 He > 0 时，正态云模型为重尾分布。

证明：正态云模型 X 的四阶中心矩为

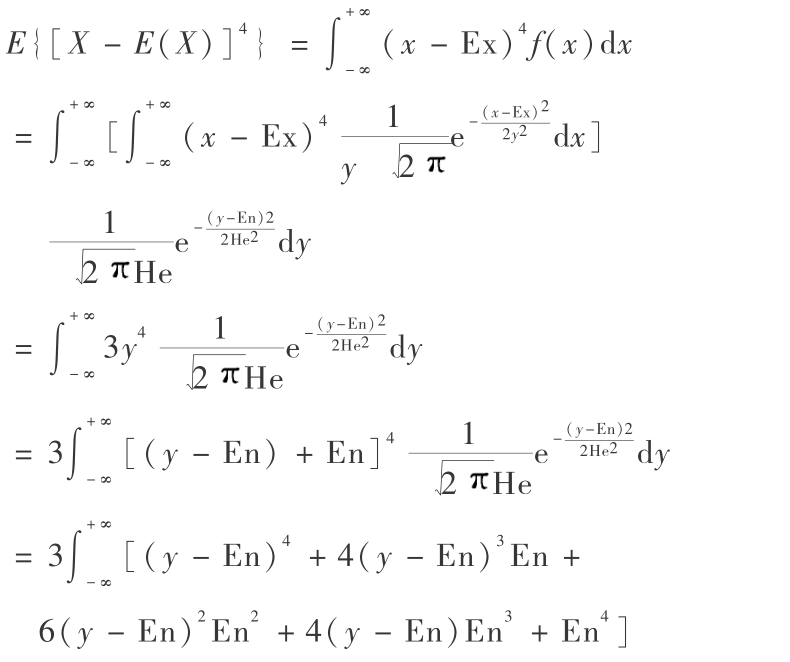
由于正态云 X 的方差 为 En2 + He2，故正态云模型的峰度为

故由定义 3，当 He > 0 时，正态云模型为重尾分布。

根据定理 1，很容易看出超熵 He 的物理意义。当 He = 0 时，正态云模型退化为正态分布。随着 He 的增大，云滴分布将由正态分布向重尾分布转换。可以说，正态云模型的数字特征超熵 He 是正态分布与重尾分布之间的桥梁。

《4 结语》

4 结语

大量的随机因素作用会导致正态分布，在自然界，完全由大量随机因素主导的现象会比较多，因此，在处理自然现象时，正态分布可能会发挥比较好的作用。而在人类社会或者有生命存在的地方，通常会存在不同程度的竞争、适者生存等因素，优先依附的准则在很多情况下适用，因此幂律分布这类重尾分布也受到了不同领域研究者的青睐。但是，人类社会中的诸多现象或者人类行为，不会完全由随机因素主宰，因为人类会理智思考，选择最利己的行动。也不会任由富者越富，大小通吃，因为会有类似国家政府的干预等因素。因此，真实的社会中，更多的现象是既存在极端事件，也有大量中间成分，是介于正态分布（平均主义）与幂律这样的重尾分布（完全不平衡） 之间的中间状态：有期望的重尾分布。可以说云模型，就是介于正态与重尾之间的中间分布。

通过笔者的研究，证明了正态云模型是一类有期望值的重尾分布。这类有平均值的重尾分布具有何种数学性质？ 其在数学领域的诸多性质证明，与其他重尾分布的比较研究，其内在形成机制的阐述证明，以及其在极端事件预测等领域的应用研究等，都将是下一步重点关注的问题。