Numerical Simulation of Static Behavior of the Single Anchor Cable

Abstract

The piecewise extrapolating method is applied to study the single anchor cable in this paper. The results are compared with the analytical results and the agreement is good. The polynomials are used to approximate the functional relations between the loads of the anchor cable and the displacement at the top of anchor cable, the water depth, and the velocity of flow on the different conditions.

Content

《1 引言》

1 引言

为了满足海上资源开发利用的需要, 海上作业平台、过驳趸船、海上浮桥及浮游码头的应用日益增加, 这些海上漂浮结构物的海上定位需要锚泊系统的约束来实现 ^[1]。在海洋和海岸工程中锚泊系统的应用十分广泛, 形式也多种多样, 但其基础为锚链顶端位置与其拉力关系和浮体运动理论。

锚链形式各种各样, 受力情况十分复杂, 通常情况下无法得出解析的表达形式, 而不得不采用数值分析的方法来实现 ^[2,3,4]。目前研究中, 对锚链系统静力分析的方法很多, 也给出了很多应用程序, 这些应用程序可以用于求解锚链系统的受力和变形, 其计算过程均需采用多次迭代的方法, 最终找到锚链顶端受力与锚链顶端位置的关系, 计算过程十分耗费机时。而在锚泊-浮体系统的实时分析中, 需要计算每一时刻物体的空间位置和锚链的拉力。这样, 在每一时刻均分析计算锚链的张力大小, 将限制分析方法的效率。

鉴于这一问题, 应用Chebyshev多项式对数值分析的锚链顶端位置和顶端拉力函数进行拟合, 求得了用于计算锚链顶端位移与受力关系的拟合公式。应用这一拟合公式可以根据锚链的顶端位置和水流速度, 方便、快速地求得锚链顶端的拉力, 从而用于波浪、水流作用下锚泊-浮体系统运动的实时模拟中。

《2 锚链系统静力分析的基本方程》

2 锚链系统静力分析的基本方程

为了说明Chebyshev多项式在锚链-浮体系统计算中的应用, 考虑一底端固定于海底, 顶端与一漂浮结构物相连的锚链为例加以说明, 对于其他的锚链形式可采用同样方法处理。

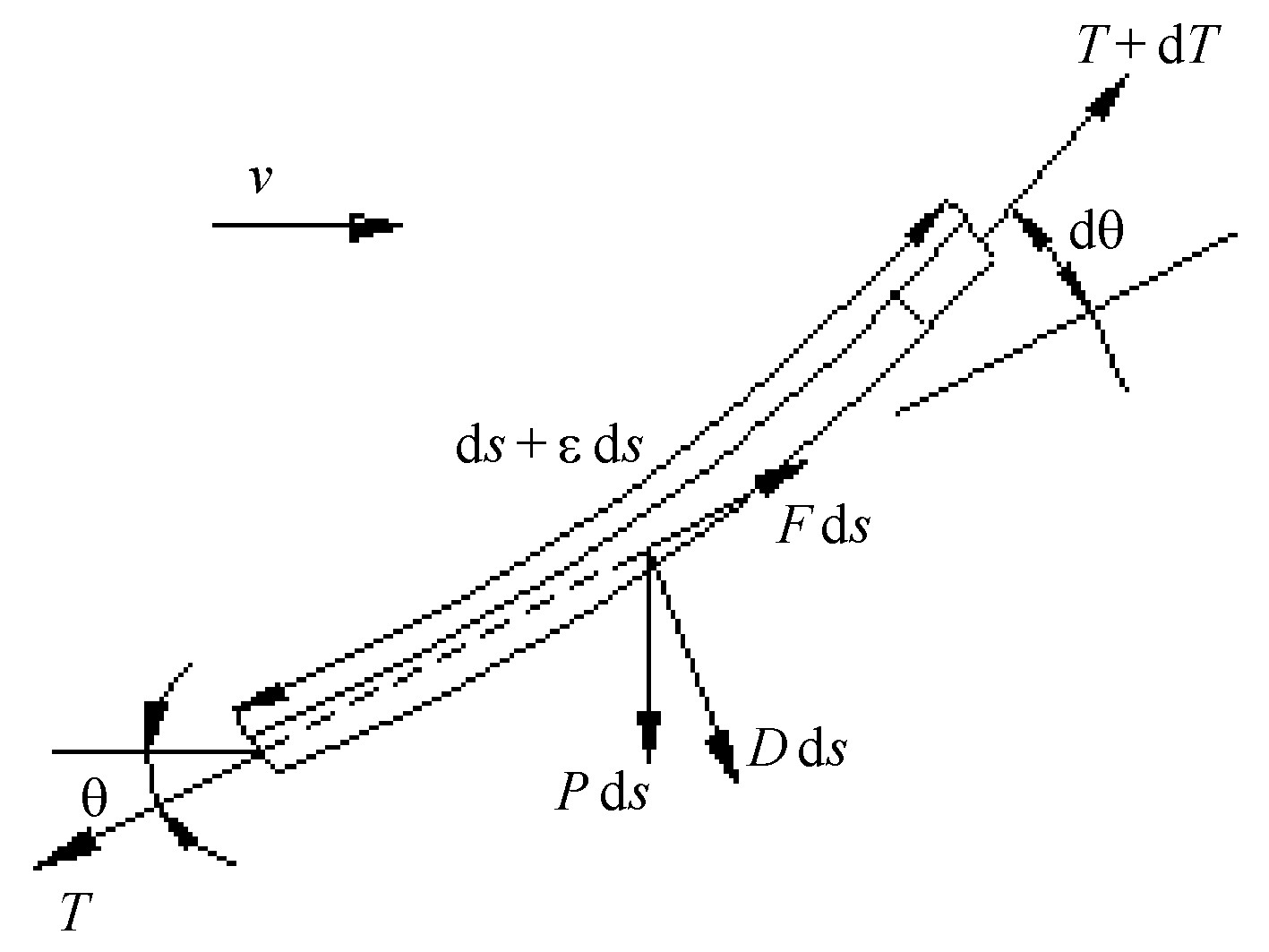
当浮体受到波浪或水流作用时, 浮体将偏离它的平衡位置, 并对锚链施加一拉力 (图1) 。如在锚链上任取一微段, 可得到这一微段在工作状态时的受力图 (图2) 。

由此可建立单元的静力平衡方程:

$\begin{array}{l} (Τ + d Τ) \cos d θ - Τ - Ρ d s s i n θ + F (1 + ε) d s = 0 (1) \\ (Τ + d Τ) \sin d θ - Ρ d s c o s θ - E (1 + ε) d s = 0 (2) \end{array}$ $\begin{array}{l} (Τ + d Τ) \cos d θ - Τ - Ρ d s s i n θ + F (1 + ε) d s = 0 (1) \\ (Τ + d Τ) \sin d θ - Ρ d s c o s θ - E (1 + ε) d s = 0 (2) \end{array}$

《图1》

图1 锚泊系统示意图

Fig.1 Sketch of mooring system

《图2》

图2 锚链上微段的受力图

Fig.2 Forces on a cable segment

其中, T为锚链受到的拉力;P为单位长度锚链的重量与浮力的合力;θ为拉力T与水平方向的夹角;E和F分别为单位长度上锚链所受的法向和切向水流力;ds为微段的长度;dT和dθ分别为拉力和角度的变化量;ε为单位长度锚链的伸长量, 定义为

$ε = \frac{Δ S}{S} = \frac{Τ}{E A} (3)$ $ε = \frac{Δ S}{S} = \frac{Τ}{E A} (3)$

E为锚链的弹性模量, A为锚链的横截面积。

忽略二阶无穷小量后可得 ^[2]

$\begin{array}{l} \frac{d Τ}{d s} = Ρ \sin θ - F (1 + ε) (4) \\ \frac{d θ}{d s} = \frac{1}{Τ} [Ρ \cos θ + E (1 + ε)] (5) \end{array}$ $\begin{array}{l} \frac{d Τ}{d s} = Ρ \sin θ - F (1 + ε) (4) \\ \frac{d θ}{d s} = \frac{1}{Τ} [Ρ \cos θ + E (1 + ε)] (5) \end{array}$

式 (1) 和式 (2) 中锚链所受的法向水流力E和切向水流力F按下列公式计算:

$\begin{array}{l} E = \frac{1}{2} ρ C_{n} D v^{2} \sin^{2} θ (6) \\ F = \frac{1}{2} ρ C_{t} π D v^{2} \cos^{2} θ (7) \end{array}$ $\begin{array}{l} E = \frac{1}{2} ρ C_{n} D v^{2} \sin^{2} θ (6) \\ F = \frac{1}{2} ρ C_{t} π D v^{2} \cos^{2} θ (7) \end{array}$

其中, v为水流速度;D为锚链直径;C_n和C_t分别为法向和切向阻力系数;ρ为水的密度。式 (4) 和式 (5) 即为所要求解的控制方程。

由微元的几何关系, 可以得到:

$\begin{array}{l} d x = (1 + ε) \cos θ d s (8) \\ d y = (1 + ε) \sin θ d s (9) \end{array}$ $\begin{array}{l} d x = (1 + ε) \cos θ d s (8) \\ d y = (1 + ε) \sin θ d s (9) \end{array}$

根据式 (8) 和式 (9) 就可以求出锚链上任意一点的坐标值 (x, y) 。

《3 锚链微分方程的求解》

3 锚链微分方程的求解

对于静水中均质锚链, 锚链微分方程可采用解析方法求解。当锚链材质不均匀且受到水流和波浪作用时, 解析解将无法找到, 因而数值方法被广泛地应用于锚链的分析计算中。采用分段外推-校正法求解锚链在各种工况下的受力特性。

《图3》

图3 锚链单元划分图

Fig.3 Descritization of mooring cable

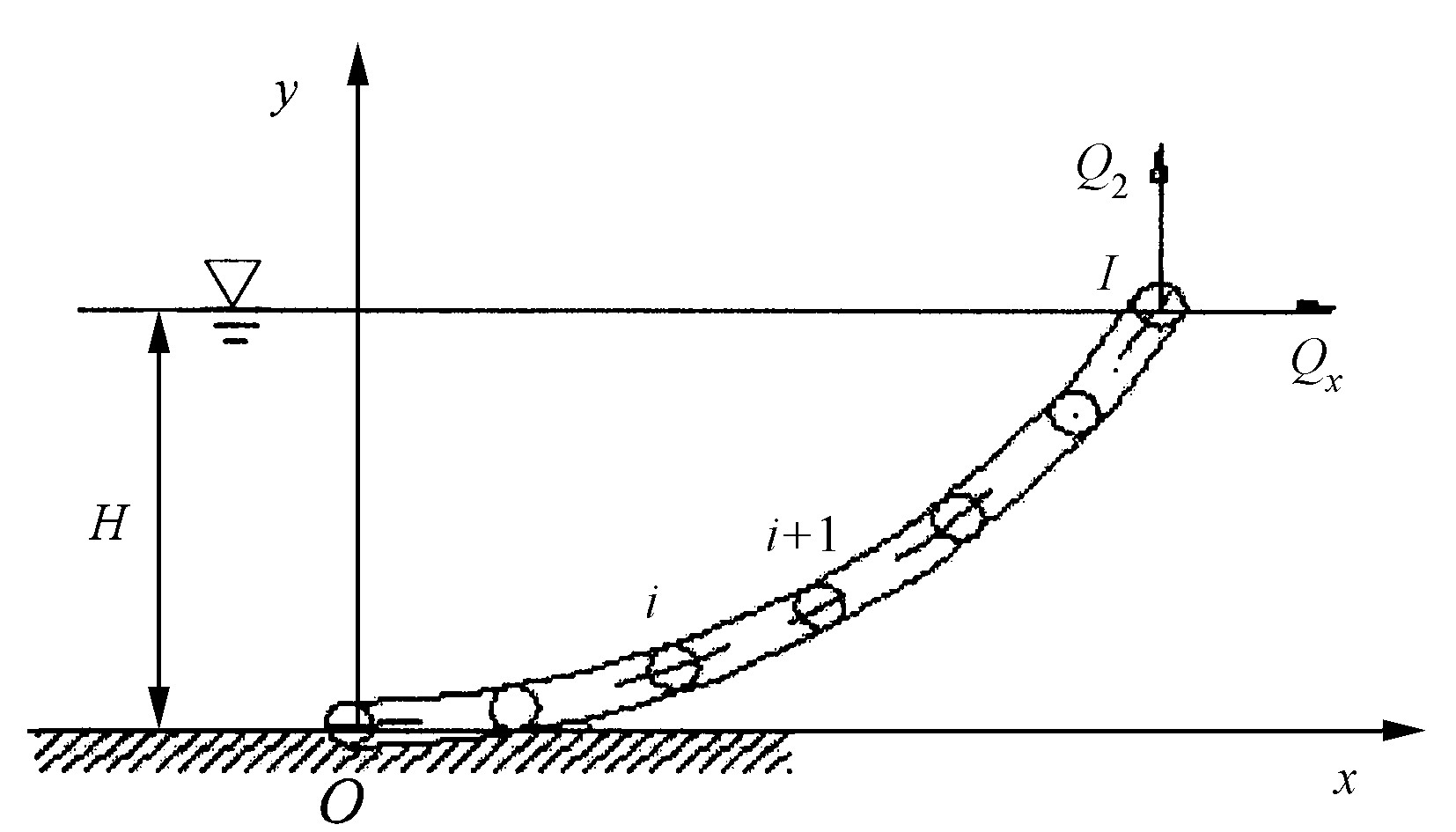
如图3所示取坐标原点在锚链与海底相交处, 并将锚链分成I个单元, 单元i左右节点的编号分别为i和i +1。作用于单元上的外力有水流力和重力 ^[3], 以及单元两端受到锚链张力, 计算中将单元重量及外荷载均集中在单元的中心上。对任意单元i进行受力分析, 如图2所示, 根据式 (4) 和式 (5) 可得到单元i上作用力的平衡方程:

$\begin{array}{l} Τ_{X ‚ i + 1} = Τ_{X ‚ i} - F_{i} \cos θ_{i} (d s + ε d s) - \\ E_{i} \sin θ_{i} (d s + ε d s) (10) \\ Τ_{Ζ ‚ i + 1} = Τ_{Ζ ‚ i} - F_{i} \sin θ_{i} (d s + ε d s) + \\ E_{i} \cos θ_{i} (d s + ε d s) + Ρ_{i} d s (11) \\ Τ_{i + 1} = (Τ_{X ‚ i + 1}^{2} + Τ_{Ζ ‚ i + 1}^{2})^{1 / 2} (12) \end{array}$ $\begin{array}{l} Τ_{X ‚ i + 1} = Τ_{X ‚ i} - F_{i} \cos θ_{i} (d s + ε d s) - \\ E_{i} \sin θ_{i} (d s + ε d s) (10) \\ Τ_{Ζ ‚ i + 1} = Τ_{Ζ ‚ i} - F_{i} \sin θ_{i} (d s + ε d s) + \\ E_{i} \cos θ_{i} (d s + ε d s) + Ρ_{i} d s (11) \\ Τ_{i + 1} = (Τ_{X ‚ i + 1}^{2} + Τ_{Ζ ‚ i + 1}^{2})^{1 / 2} (12) \end{array}$

式中, T_{X, i}和T_{Z, i}为第i单元的左端水平和垂向张力;F_i和D_i分别为第i单元的切向和垂向上单位长度的水流力。根据式 (8) 和式 (9) 可得到单元节点坐标的空间关系为

$\begin{array}{l} x_{i + 1} = (d s + ε d s) \cos θ_{i} + x_{i} (13) \\ y_{i + 1} = (d s + ε d s) \sin θ_{i} + y_{i} (14) \end{array}$ $\begin{array}{l} x_{i + 1} = (d s + ε d s) \cos θ_{i} + x_{i} (13) \\ y_{i + 1} = (d s + ε d s) \sin θ_{i} + y_{i} (14) \end{array}$

以上公式可以变换成下面的形式:

$\begin{array}{l} Τ_{X ‚ i} = Q_{X} - \sum_{k = i}^{Ι} F_{x, k} (15) \\ Τ_{Ζ ‚ i} = Q_{Ζ} - \sum_{k = i}^{Ι} (F_{z, k} - Ρ_{Κ}) (16) \\ Τ_{i} = ((Q_{X} - \sum_{k = i}^{Ι} F_{x, k})^{2} + \\ (Q_{Ζ} - \sum_{k = i}^{Ι} (F_{(z, k)} - Ρ_{k}))^{2})^{1 / 2} (17) \end{array}$ $\begin{array}{l} Τ_{X ‚ i} = Q_{X} - \sum_{k = i}^{Ι} F_{x, k} (15) \\ Τ_{Ζ ‚ i} = Q_{Ζ} - \sum_{k = i}^{Ι} (F_{z, k} - Ρ_{Κ}) (16) \\ Τ_{i} = ((Q_{X} - \sum_{k = i}^{Ι} F_{x, k})^{2} + \\ (Q_{Ζ} - \sum_{k = i}^{Ι} (F_{(z, k)} - Ρ_{k}))^{2})^{1 / 2} (17) \end{array}$

式中, Q_X, Q_Z为锚链顶端在x, z方向受到的拉力分量。

在求解过程中采用迭代方法, 计算过程如下:

Step 1 已知顶端高度H、锚链顶端的水平拉力Q_X和水流速度v,

Step 2 把锚链划分成若干个单元,

Step 3 假设锚链顶端切线与水平方向的夹角θ已知;

Step 4 计算每个单元上的重力和水流力;

Step 5 根据式 (13) 、式 (14) 、式 (17) 求出锚链上各段的受力T和各点的坐标值 (x, y) ;

Step 6 最后验证水深边界条件 (也就是最后一点坐标y = H, H为水深) , 如果满足这个边界条件, 则计算结束, 否则返回步骤Step 3, 调整锚链顶端切线与水平方向的夹角, 重复计算, 直到满足一定精度为止。

首先对锚链分段, 对每一段进行求解, 然后外推, 经多次校正后求得最终的精确结果, 因此称为分段外推-校正法。

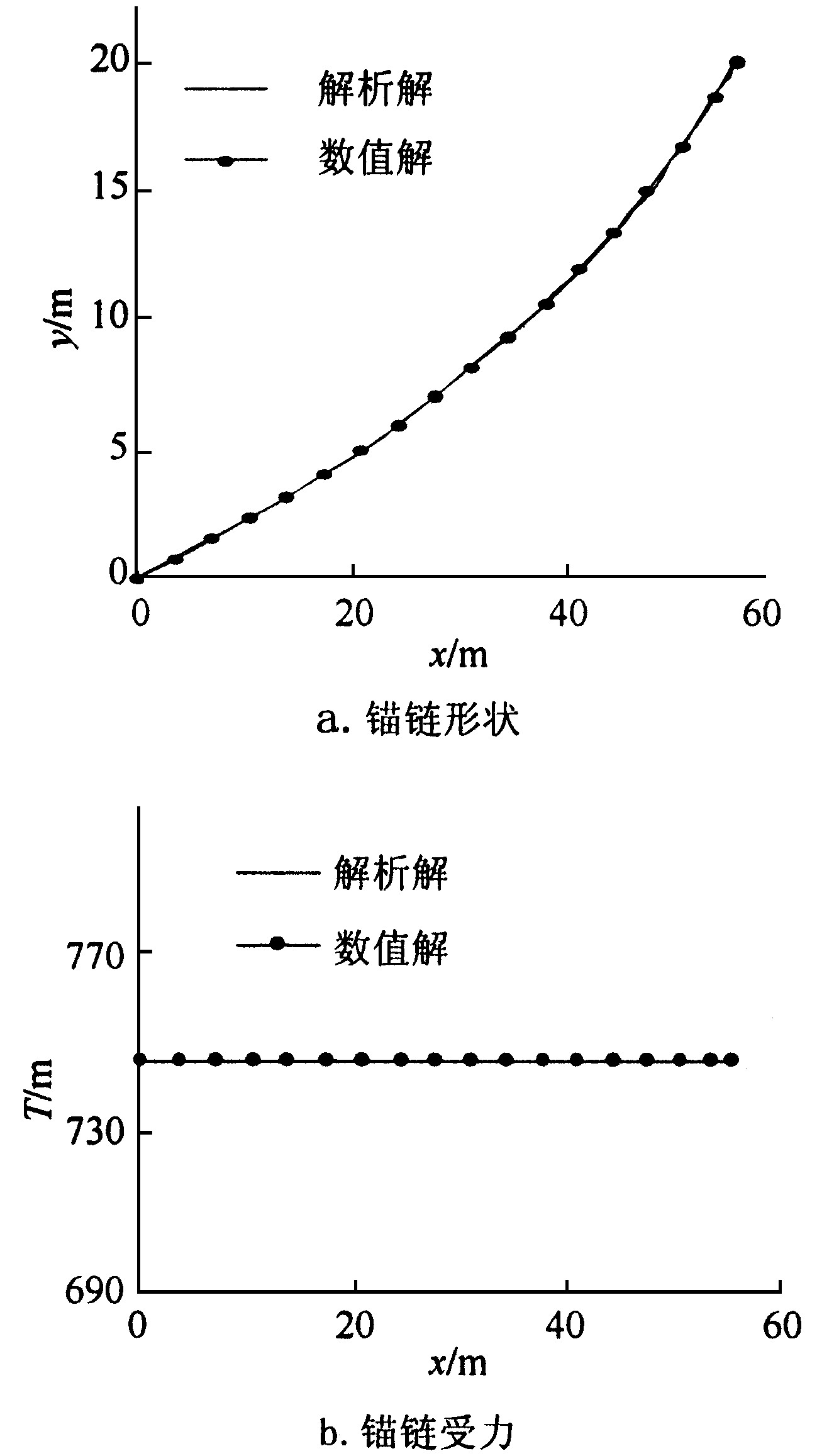
图4为关于静水中一均匀锚链, 应用分段外推-校正法所计算的锚链形状和锚链张力力曲线和解析解的比较。锚链长59.2 m, 直径0.05 m, 锚链顶端高度20 m, 顶端受到拉力的水平分量为0.6 kN, 水流速度v=0 m/s。从图4可见, 数值方法计算的锚链张力和形状曲线与解析解吻合得很好, 表明分段外推-校正法的计算结果很精确, 可用于求解锚链受力和锚链顶端所固定物体的位移。

《4 锚链函数的Chebyshev多项式拟合》

4 锚链函数的Chebyshev多项式拟合

运用分段外推-校正法对锚链进行分析时, 已知条件为锚链的顶端高度和锚链顶端的水平拉力, 坐标原点为锚链与地面的接触点。而在浮体-锚链系统的实时模拟中需要根据浮体的空间位置, 确定锚链对浮体的作用力, 然后根据牛顿定律计算浮体的加速度, 依据时间步进技术计算浮体的运动速度和浮体的新的空间位置。当应用上述分段外推- 校正法计算锚链拉力时, 需先假设锚链的水平拉力, 经过迭代得到正确的锚链曲线, 然后判断锚链顶端的水平位置是否与浮体上的连接位置一致, 不一致时需迭代求解以得到收敛结果。这样, 当浮体每运动到一新的空间位置, 就需要对锚链做两重迭代计算, 需要大量的计算时间。为了满足工程中的实际应用, 利用了多项式拟合方法, 根据分段外推-校正法得出锚链受力与顶端位置的多项式表达关系, 应用该多项式表达式可根据浮体的空间位置直接内插求解确定锚链的张力。

《图4》

图4 数值结果与解析解的对比

Fig.4 Comparison between numerical results and analytic solution

《4.1 Chebyshev多项式拟合》

4.1 Chebyshev多项式拟合

Chebyshev多项式是在区间[-1, 1]上逼近任一函数的一种重要工具, 被称为最大最小逼近函数, 与其他函数相比它可以保证在插值区间内最大误差为最小。对于一维函数f (x) , 可计算其近似值为 (William ^[5])

$f (x) = [\sum_{j = 1}^{Ν} c_{j} Τ_{j - 1} (x)] - \frac{1}{2} c_{1} (18)$ $f (x) = [\sum_{j = 1}^{Ν} c_{j} Τ_{j - 1} (x)] - \frac{1}{2} c_{1} (18)$

式中c_j为Chebyshev多项式的展开系数 (j = 1, 2, …, N) 。

其中n次Chebyshev多项式用T_n (x) 表示。T_n (x) 定义为

$Τ_{n} (x) = \cos (n a r c c o s x) = \sum_{i = 0}^{n} a_{n i} x^{i} (19)$ $Τ_{n} (x) = \cos (n a r c c o s x) = \sum_{i = 0}^{n} a_{n i} x^{i} (19)$

a_ni为Chebyshev多项式系数, 其定义见文献[6]。

当自变量范围为[a, b] 时, 可采用线性变换将其转化到[-1, 1] 内, 最后利用Chebyshev多项式的正交性计算出Chebyshev展开系数

$c_{j} = \frac{ε_{k}}{Ν} \sum_{k = 0}^{Ν} f (x_{k}) Τ_{j - 1} (x_{k}) i = 1, 2, \dots, Ν (20)$ $c_{j} = \frac{ε_{k}}{Ν} \sum_{k = 0}^{Ν} f (x_{k}) Τ_{j - 1} (x_{k}) i = 1, 2, \dots, Ν (20)$

式中x_k为Chebyshev插值基点,

$ε_{k} = {\begin{cases} 1 k = 0 ‚ \\ 2 k > 0 。 \end{cases}$ $ε_{k} = {\begin{cases} 1 k = 0 ‚ \\ 2 k > 0 。 \end{cases}$

《4.2 转换成普通多项式》

4.2 转换成普通多项式

为了进一步提高计算效率, 可将Chebyshev多项式 (18) 转换成普通多项式的情况

$f (x) = \sum_{i = 1}^{Μ} p_{i} x^{i - 1} (21)$ $f (x) = \sum_{i = 1}^{Μ} p_{i} x^{i - 1} (21)$

上式中的系数p_i由Chebyshev多项式系数a_i和多项式展开系数c_j转化而来

$p_{i} = \sum_{m = i}^{Ν} c_{m} a_{m i} (22)$ $p_{i} = \sum_{m = i}^{Ν} c_{m} a_{m i} (22)$

对于二维情形有

$f (x, y) = \sum_{i = 1}^{Μ} \sum_{j = 1}^{Ν} p_{i j} x^{i - 1} y^{j - 1} (23)$ $f (x, y) = \sum_{i = 1}^{Μ} \sum_{j = 1}^{Ν} p_{i j} x^{i - 1} y^{j - 1} (23)$

式中的系数p_ij为

$p_{i j} = \sum_{m = i}^{Μ} \sum_{n = j}^{Ν} c_{m n} a_{m i} a_{n j} (24)$ $p_{i j} = \sum_{m = i}^{Μ} \sum_{n = j}^{Ν} c_{m n} a_{m i} a_{n j} (24)$

对于三维情形有

$f (x, y, z) = \sum_{i}^{L} \sum_{j}^{Μ} \sum_{k}^{Ν} p_{i j k} x^{i - 1} y^{j - 1} z^{k - 1} (25)$ $f (x, y, z) = \sum_{i}^{L} \sum_{j}^{Μ} \sum_{k}^{Ν} p_{i j k} x^{i - 1} y^{j - 1} z^{k - 1} (25)$

式中的系数p_ijk为

$p_{i j k} = \sum_{l = i}^{L} \sum_{m = j}^{Μ} \sum_{n = k}^{Ν} c_{l m n} a_{l i} a_{m j} a_{n k} (26)$ $p_{i j k} = \sum_{l = i}^{L} \sum_{m = j}^{Μ} \sum_{n = k}^{Ν} c_{l m n} a_{l i} a_{m j} a_{n k} (26)$

《图5》

图5 坐标系选取示意图

Fig.5 Definition of Coordinate System

《4.3 锚链张力函数的多项式展开》

4.3 锚链张力函数的多项式展开

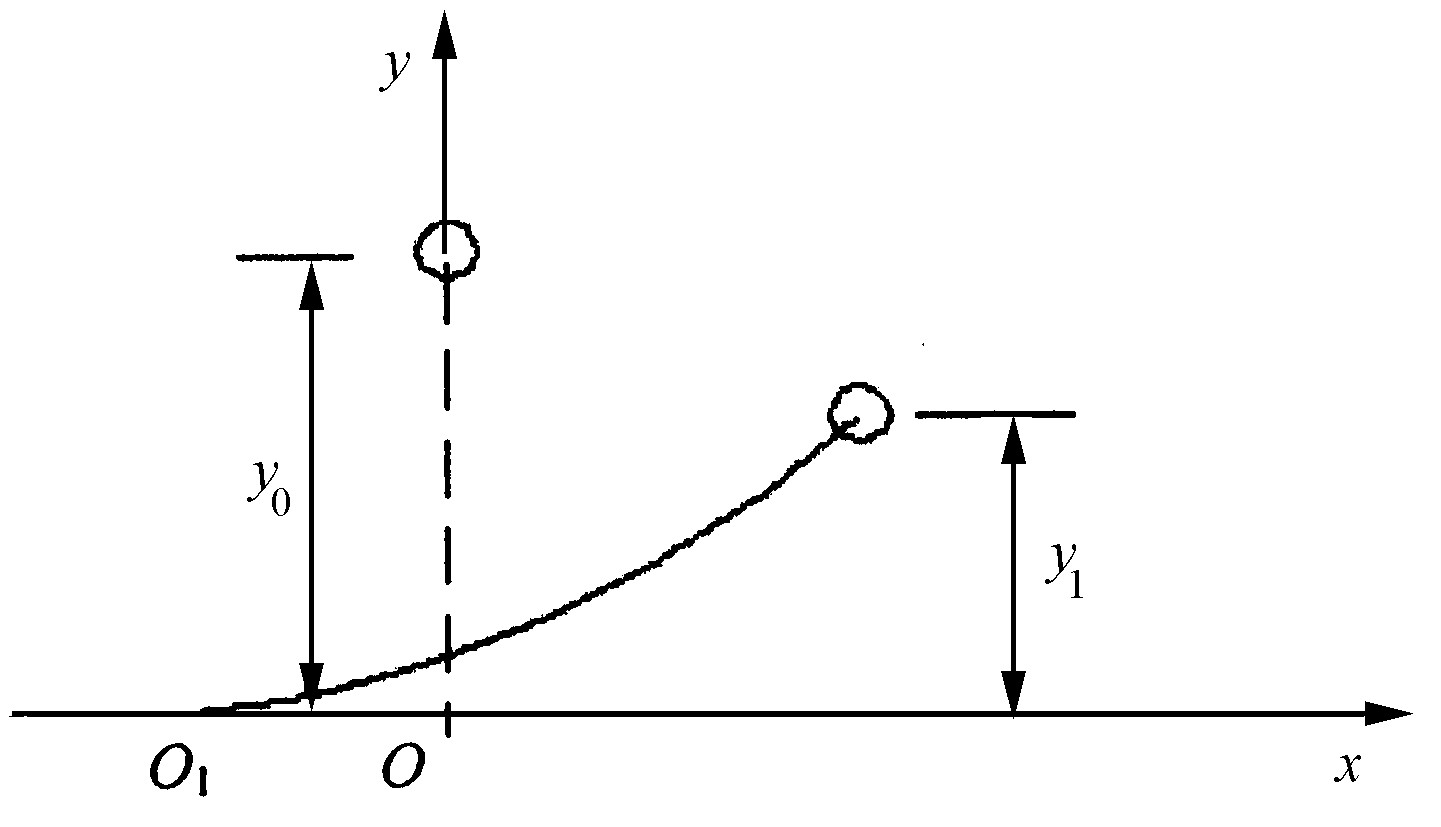
对锚链受力函数进行拟合时的坐标系选取如图5所示。坐标原点O取在锚链顶端高度为y₀且自然下垂时与海底的交点。O₁为锚链顶端高度为y₁, 且收到拉力拉起时锚链与海底的交点, 该坐标系随锚链顶端位置的变化而变化。在锚链张力函数的建立中统一采用空间固定的Oxy坐标体系。

1) 无水流作用

无流作用时, 锚链顶端受力是锚链顶端水平坐标x和高度y的函数。采用Chebyshev多项式对锚链顶端水平和垂向拉力对x和y进行拟合, 最终把锚链顶端水平和垂向拉力表示为锚链顶端位置x, y的函数。这样对锚链顶端固定的结构物处于任意水深和水平坐标x时, 都可以应用系数表直接进行插值求解。

2) 有水流作用

当考虑水流作用时, 锚链受力的大小取决于水平坐标x、纵坐标y和水流流速v。同样用多项式对有流作用下的锚链受力进行拟合, 最终把锚链顶端水平和垂向拉力表示为x, y和v的函数, 这样对于流速v中锚链顶端处于任意的水平坐标x、高度y时, 就可以直接进行内插求解。

《5 数值结果》

5 数值结果

利用上述提出的方法, 研究了无水流和有水流作用的两种情况下, 不同顶端高度、不同流速对锚链顶端水平和竖直方向受力的影响, 锚链坐标原点取顶端高度y=30 m且自由下垂时与海床的交点。

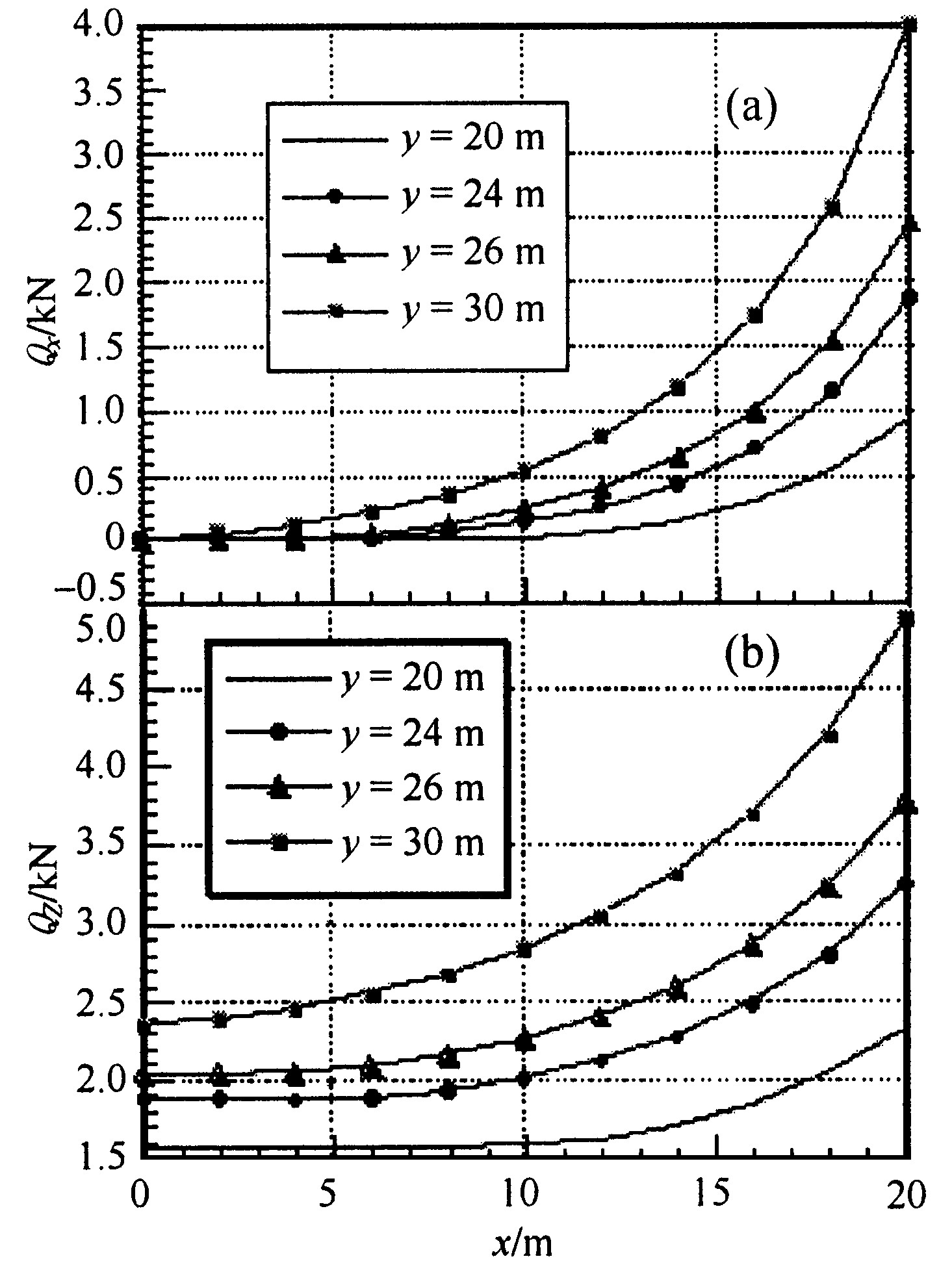
图6为锚链足够长情况下, 没有水流作用时, 在不同顶端高度情况下, 锚链顶端所受水平力、竖直力与其水平坐标的关系图。锚链单位长重力与浮力的差值为P=7.796 kg/m³。从计算结果中可以看出, 随着水深的增加锚链顶端受力也随之增加。另外, 随着水平坐标的增大锚链顶端受力也随之增大, 但两者呈非线性关系。

《图6》

图6 水深不同时锚链顶端水平坐标与受力关系图

Fig.6 Forces of different water depth

a.水平方向;b.竖直方向

图7为有水流作用下, 水流流速分别为0.1 m/s和0.3 m/s时, 不同锚链顶端高度的锚链顶端受力图。锚链单位长重力与浮力的差值为P=7.796 kg/m³, 直径0.038 m。从图7中可以看到随着水深的增加锚链顶端的受力也随之增大。

《图7》

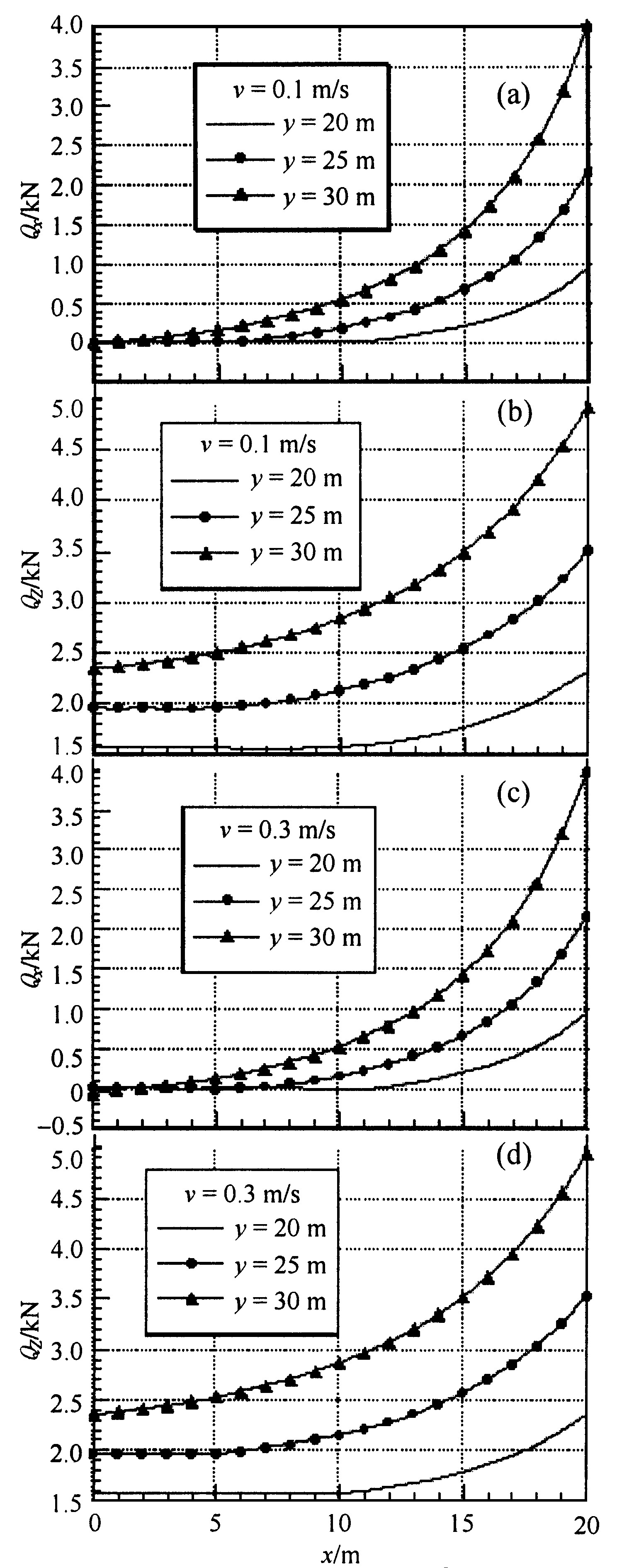
图7 水流作用下水深不同时锚链顶端受力图

Fig.7 Forces of anchor cable different water depth under the effect of water flow

a.水平方向受力图;b.竖直方向受力图;c.水平方向受力图;d.竖直方向受力图

图8是锚链顶端高度20 m, 流速分别为0 m/s, 0.1 m/s, 0.3 m/s时, 顶端固定结构物, 直径为0.038 m锚链顶端的受力结果图。锚链单位长重力与浮力的差值为P=7.796 kg/m³。从图8中可以看到, 随着水平坐标的增大锚链顶端受力也随之增大, 两者呈非线性关系。当流速很小时, 锚链顶端受力随着流速的增大变化不明显。

《图8》

图8 不同流速作用下锚链顶端受力图

Fig.8 Forces of anchor cable under the effect of water flow

a.水平方向受力图;b.竖直方向受力图

《6 结语》

6 结语

依据Chebyshev多项式拟合和分段外推-校正的数值计算方法, 对静水和水流中锚链, 建立了锚链张力与锚链顶端位置的多项式函数表达关系, 该多项式表达关系可方便、快速地用于波浪、水流与锚链-浮体系统相互作用的实时模拟中。

应用锚链拉力与顶端位置的多项式函数, 对静水和水流中的单根锚链做了计算, 计算结果表明:

1) 无水流作用时, 锚链顶端受力随着锚链顶端水平位置的增加呈非线性增大, 锚链顶端受力随着顶端高度的增加而增大。

2) 有水流作用下, 锚链顶端的受力随着锚链顶端水平坐标的增大呈非线性增大, 锚链顶端受力随着水深的增大而增大。

3) 当流速比较小时, 流速的变化对锚链顶端水平和竖直力的影响不明显。

《图9》

Show More