《1 引言》
1 引言
直立防波堤和码头是海岸工程中常见的结构 形式。近年来透空结构引起了人们的注意,并被应 用在防波堤和码头的建设中,在二维透空结构方面 进行了大量研究。Yang, [1]Twu和Lin[2]等研究了 多块透空板对波浪的反射和透射问题;Madsen[3], Zhu和Chwang [4]等研究了波浪与前壁开孔沉箱的 作用问题;Chwang[5]还研究了透水推板的造波原 理和特性;Dalrymple和Martini[6], Yu[7] 研究了 波浪对透水半无限防波堤的绕射作用;吴建华 等[8]研究了直墙上水平渗透横板对波浪反射的影响。
应用多块透空板或前壁开孔沉箱作为防波堤有两点好处。首先,不透水堤前的波浪力被分解为分别作用在前后壁上,并具有相位差的两个部分,前后壁上波浪力相位差的大小,取决于前后壁间的距 离和波浪长度。适当选择两壁间的距离,可以使作 用在两壁上的波浪力相互减弱,从而减小作用在整 个建筑物上的作用力。其次,波浪穿过透空板时产率 和波面高度。
在二维透空式结构的研究中,通常假定透空壁 为不变型的均匀“海绵”式透空体。波浪运动通过 “海绵”体时,假定流体的运动速度与“海绵”体 两边的压力差成正比,比例系数由流体的粘性、惯 性和开孔率等因素决定[3,9~11]。
相对于二维问题而言,对三维问题的研究较少。在这方面的工作,只见到了 Wang和Ren[12], Darwiche等[13]和 Williams等[14]的研究成果。 Wang和Ren研究了外筒为均匀透空的双筒柱问题,Darwiche等研究了外壁上部为透空壁的双筒柱问题;Williams等研究了上部和下部分别开孔的漂浮直立圆柱问题。他们的研究对象都是在环向均匀开孔的圆柱。
实际工程应用中,透空式墩柱常常设计成迎浪 侧开孔,而背浪侧不开孔。对于这样的问题,本文 建立了波浪与外壁部分透空双蚪柱绕射的线性解析 解。透空部分沿环向占一部分或几个部分,但沿水 深方向均匀分布。研究中,应用了透水壁内流速与其壁两侧间压力差成正比的线性假设。圆柱外流域中和内外柱间的速度势展开成特征函数的表达式,展开系数由内外圆柱表面条件和外壁匹配条件确定。应用该模型开展了数值计算,检验了不同孔隋系数和内外半径之比对作用在双筒柱上波浪力和波面升高的影响。数值结果表明在一定频率范围内,外壁的开孔率和孔隙大小对冶小波浪荷载和波面升高有显著作用,而在其他一些频率下,波面的升高和波浪荷载较实体圆柱为大。
《2 控制方程和边界条件》
2 控制方程和边界条件
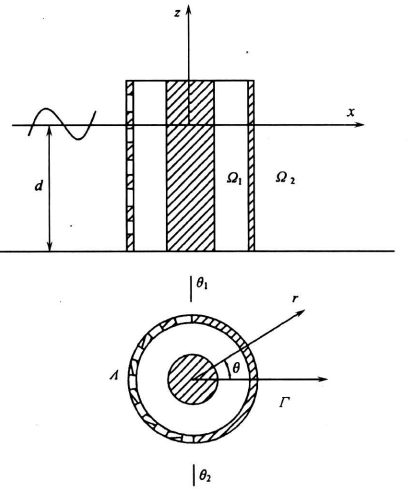
考虑波濒与同轻直立双筒柱的作用问题(见图1)。内柱密实不透水,半径为b,外壁半径为a,在环向ω(θ1到θ2)区段为透空结构,而在工区段为密实不透水,外壁透空部分在水深方向均匀分布,且厚度与波长相比很小,可以忽略。采用柱坐标系(r,θ,z),坐标原点位于柱轴线与静水面交汇处。
《图1》

图1 结构定义图
Fig.1 Definition sketch
圆柱受到一列波幅为A、频率为ω、沿z轻正向传播的小波幅规则波的作用。在流域内,忽略水体粘性并假设流体做无旋运动,因此速度势漾足拉普拉斯方程。对于入射频率为ω。的规则波,分离出时间因子e-iwt仪,而将速度势写为
\(\Phi(x, t)=\operatorname{Re}\left[\phi(x) e^{-\mathrm{i} \omega t}\right] \)。 (1)
为研究方便,将流域分为内域\(\Omega_{1}\)和外域\(\Omega_{2}\)两个子域,复速度势\(\phi_{j}\)满足拉普拉斯方程:
\(\nabla^{2} \phi_{j}=0 ; j=1,2,\), (2)
下标j表示流域\(\Omega_{j}\)内的物理量。速度势还应满足自由水面、海底、柱面及无限远处的边界条件。
在自由水面上,满足的自由水面条件为
\(\frac{\partial \phi_{j}}{\partial z}=\frac{\omega^{2}}{g} \phi_{j} ; z=0, j=1,2\)。 (3)
在水平不透水海床上,满足的不透水条件为
\(\frac{\partial \phi_{j}}{\partial z}=0 ; z=-d, j=1,2\)。 (4)
在不透水内柱上,满足
\(\frac{\partial \phi_{1}}{\partial r}=0 ; r=b\)。 (5)
在外柱上,满足的边界条件和匹配条件为
\(\frac{\partial \phi_{1}}{\partial r}=\frac{\partial \phi_{2}}{\partial r} ; r=a\)。 (6)
\(\frac{\partial \phi_{1}}{\partial r}=\left\{\begin{array}{clrl}0 ; & r & =a, \quad \theta \in \Gamma \\i k G\left(\phi_{1}-\phi_{2}\right) ; & r & =a, \quad \theta \in \Lambda_{0}\end{array}\right.\)。 (7)
式中g表示重力加速度,k为波数,系数G=GR+iGI取决于流体的粘性,外柱壁的厚度和柱壁上开孔率等因素。波数k与波浪角频率ω,满足弥散关系
\(\omega^{2}=g k \tanh k d\)。 (8)
《3 解析分析》
3 解析分析
在外部区域\(\Omega_{2}\)上,将速度势\(\phi_{2}\)分解为入射势\(\phi_{I}\)和绕射势\(\phi_{D}\)两个部分。在柱坐标系下,θ=0轴与波浪入射方向一致,入射势可以写为
\(\phi_{I}=-\frac{\mathrm{igA}}{\omega} Z(z) \sum_{m=0}^{\infty} \varepsilon_{m} \mathrm{i}^{m} J_{m}(k r) \cos m \theta\)。 (9)
式中A为入射波波帽,为Neumman系数(当m=0时,εm=1;当m>0时,εm=2),垂向特征函数为\(Z(z)=\cosh k(z+d) / \cosh k d \),对于外柱面边界条件式(6)和式(7),外域上的绕射势将不包括局部非传播模态。考虑到散射波向外传播的远场条件,外域的绕射势可写为
\(\phi_{\mathrm{D}}=-\frac{\mathrm{i} g A}{\omega} Z(z) \sum_{m=0}^{\infty} \varepsilon_{m} \mathrm{i}^{m} A_{m} \mathrm{H}_{m}^{(1)}(k r) \cos m \theta\)。 (10)
式中Hm(1)(x)为第一类Hankel函数,对应于向外传播的波浪。在内部区域\(\Omega_{1}\)中,速度势可以写为\(\begin{array}{l}\phi_{1}=-\frac{\mathrm{igA}}{\omega} Z(z) \sum_{m=0}^{\infty} \varepsilon_{m} \mathrm{i}^{m} \dot\\{\left[C_{m} \mathrm{H}_{m}^{(1)}(k r)+D_{m} \mathrm{H}_{m}^{(2)}(k r)\right] \cos m \theta } \\\end{array}\)。 (11)
式中Hm(2)(x)表示第二类Hankel函数,对应于向轴心方向传播的波浪。将内部区域的速度势代入边界条件式(5),有
\(\begin{array}{l}\quad \sum_{m=0}^{\infty} \varepsilon_{m} \mathrm{i}^{m} \cos m \theta\left[C_{m} \mathrm{H}_{m}^{(1) \prime}(k b)+D_{m} \mathrm{H}_{m}^{(2) \prime}(k b)\right]=0 \end{array}\)。 (12)
由此可得到:
\(D_{m}=-C_{m} \frac{\mathrm{H}_{m}^{(1)^{\prime}}(k b)}{\mathrm{H}_{m}^{(2)^{\prime}}(k b)} \quad m=0,1,2, \cdots_{\circ}\) (13)
当内柱半径趋于0时,Dm趋于Cm。
定义Fm(x)为
\(F_{m}(x)=\mathrm{H}_{m}^{(1)}(x)-\frac{\mathrm{H}_{m}^{(1) \prime}(k b)}{\mathrm{H}_{m}^{(2)^{\prime}}(k b)} \mathrm{H}_{m}^{(2)}(x)\)。 (14)
这样,内部区域\(\Omega_{1}\)上的速度势可写为
\(\phi_{1}=-\frac{\mathrm{i} g A}{\omega} Z(z) \sum_{m=0}^{\infty} \varepsilon_{m} \mathrm{i}^{m} C_{m} F_{m}(k r) \cos m \theta\)。 (15)
分别将内、外域上的速度势代人边界条件式(6)和式(7),得到:
\(\begin{array}{c}\sum_{m=0}^{M} m \mathrm{i}^{m} \cos m \theta\left[J_{m}^{\prime}(k a)+A_{m} \mathrm{H}_{m}^{(1) \prime}(k a)\right]= \\\sum_{m=0}^{M} \varepsilon_{m} \mathrm{i}^{m} \cos m \theta C_{m} F_{m}^{\prime}(k a) ;\end{array}\) (16)
\(\begin{array}{l}k \sum_{m=0}^{M} \varepsilon_{m} \mathrm{i}^{m} \cos m \theta\left[J_{m}^{\prime}(k a)+A_{m} \mathrm{H}_{m}^{(1)}(k a)\right]= \\\left\{\begin{array}{l}0, \quad \theta \in \Gamma, \\\mathrm{i} k G \sum_{m=0}^{M} \varepsilon_{m} \mathrm{i}^{m} \cos m \theta\left[C_{m} F_{m}(k a)-\right. \\\left.J_{m}(k a)-A_{m} \mathrm{H}_{m}^{(1)}(k a)\right], \quad \theta \in \Lambda_{\circ}\end{array}\right.\end{array}\)。 (17)
由此,得到联立线性方程组
\(A_{m} \mathrm{H}_{m}^{(1) \prime}(k a)-C_{m} F_{m}^{\prime}(k a)=-J_{m}^{\prime}(k a)\) (18)
\({\left[a_{n m}\right]\left\{A_{m}\right\}-\left[c_{n m}\right]\left\{C_{m}\right\}=} \\-\left[d_{n m}\right]\left\{J_{m}(k a)\right\}-\left\{2 \pi \mathrm{i}^{n} J_{n}^{\prime}(k a)\right\}\), (19)
式中
\(\begin{array}{l}d_{n m}=\varepsilon_{m} \mathrm{i}^{m+1} G E_{n m}, \\a_{n m}=\left\{\begin{array}{lr}d_{n m} \mathrm{H}_{m}^{(1)}(k a), \\d_{n m} \mathrm{H}_{m}^{(1)}(k a)+2 \pi \mathrm{i}^{m} \mathrm{H}_{m}^{(1) \prime}(k a), m=n,\end{array}\right. \\c_{n m}=d_{n m} F_{m}(k a), \\E_{n m}=\int_{\Lambda} \cos n \theta \cos m \theta \mathrm{d} \theta \circ\end{array}\)
由联立方程组式(18)和式(19),可求得系数Am和Cm,最终确定桩柱内部和外部的速度势。
《4 波浪荷载和波面高度》
4 波浪荷载和波面高度
求得了速度势之后,桓柱表面上的波动压力可由贝努力方程计算,圆柱上的波浪荷载可由壁面上的压力积分得到。在一阶波陡的近似下,内柱上的波浪力可写为:
\(f_{\mathrm{b}}=-\int_{s_{b}^{+}} p_{1} \cos \theta \mathrm{d} s=-2 \pi \mathrm{i} \rho g A b \frac{\tanh k d}{k} C_{1} F_{1}(k b)\) (20)
式中ρ为流体密度,Sb+表示内柱壁的外表面。外柱上的波浪力可写为
\(\begin{array}{c}f_{a}=-\int_{s_{a}^{+}} p_{2} \cos \theta \mathrm{d} s \int_{s_{a}^{-}} p_{1} \cos \theta \mathrm{d} s= \\-2 \pi \mathrm{i} \rho g A a \frac{\tanh k d}{k}\left[J_{1}(k a)+\cdot\right. \\\left.A_{1} \mathrm{H}_{1}^{(1)}(k a)-C_{1} F_{1}(k a)\right]\end{array}\), (21)
\(S_{a}^{-}\)和\(S_{a}^{+}\)表示外柱的内、外表面。作用在圆柱上总的波浪力为:
\(f_{\mathrm{T}}=f_{\mathrm{a}}+f_{\mathrm{b}}\)。 (22)
在一阶波降近似下,柱内波面高度为
\(\eta_{1}=A \sum_{m=0}^{\infty} \varepsilon_{m} \mathrm{i}^{m} C_{m} F_{m}(k r) \cos m \theta\) (23)
柱外波面高度为:
\(\eta_{2}=A \sum_{m=0}^{\infty} \varepsilon_{m} \mathrm{i}^{m}\left[J_{m}(k r)+A_{m} \mathrm{H}_{m}^{(1)}(k r)\right] \cos m \theta\) (24)
《5 数值结果》
5 数值结果
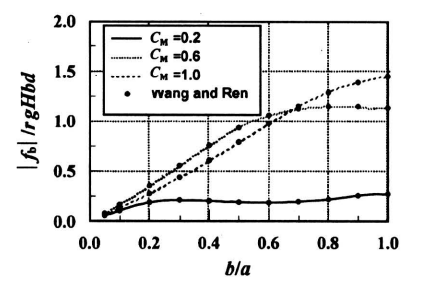
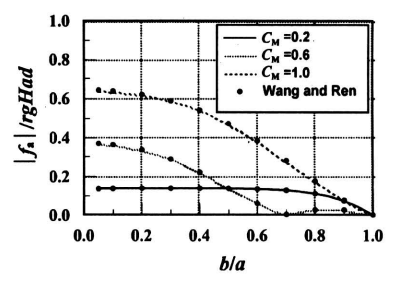
为了验证本方法和数值模型的正确性,首先取一外柱为全部透空的双筒圆柱作了计算,并与Wang和Ren[12]的结果作了对比,计算水深为d/a=1.5,波浪参数Cw=g/ω2d,外壁透空系数取G=1.0,图2和图3分别为内外柱上波浪作用力,从中可以看到本文结果与Wang和Ren的结果吻合良好。
为了检验透空壁对作用在圆柱上波浪荷载和波浪爬高的影响,取两种类型的圆柱作了计算。国柱A的外简从θ=π/2到θ=3π/2段为透空壁,即外壁的一半为透空结构;国柱B的外简从θ=0到θ=2π段为透空壁,即整个外壁全为透空结构,水深都为d/a=1.0。
《图2 》

图2 双筒柱内筒上波浪力随内筒半径的分布d/a = 1.0, G = 1.0
Fig.2 Wave force on the interior column of a two-column porous cylinder at d/a = 1.0 and G = 1.0
《图3》

图3 双筒柱外筒上波浪力随内筒半径的分布 d/a = 1.0, G = 1.0
Fig.3 Wave force on the exterior column of a two-column porous cylinder at d/a = 1.0 and G= 1.0
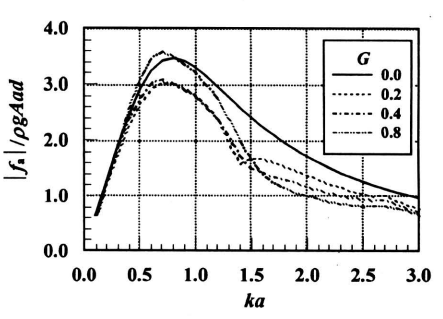
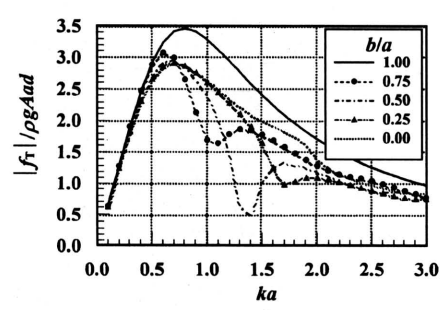
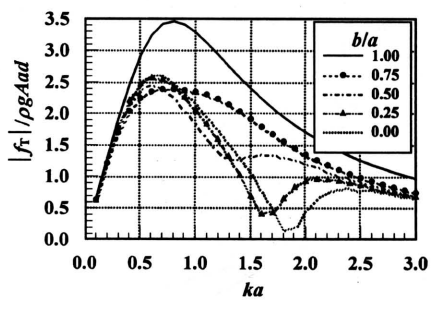
图4为作用在A柱外简上的波浪力,圆简内径为d/a=0.5,孔随系数的形式为G=GR。在低频区,波浪力随孔隙系数GR的增加而略微减小,然后随GR的增加而增大;在高频区,波浪力随GR的增加而减小。图5为相应内筒上的波浪力,内简上的波浪力随孔隙系数GR的增加而增大,在波数ka=1.4附近出现最大值。图6为整个圆柱上的波浪力,在低频区透空壁对冶小波浪力的作用不明显,在高频区波浪力随孔歌系数的增加而明显减小。在ka=1.4附近,波浪荷载分布忽然下降。图7为作用在圆柱B上的总波浪力。对于外简全部透空的圆柱,无论在较低或较高频率下,整个国柱上的波浪力都随外壁孔隙系数的增加而减小。
《图4 》

图4 双筒柱A外筒上的波浪力随波数ka的分布
Fig.4 Wave force on the exterior column of cylinder A
《图5 》

图5 双筒柱A内筒上的波浪力 随波数ka的分布
Fig.5 Wave force on the interior column of cylinder A
图8为具有不同尺寸内简A柱上的总的波浪力,外壁孔隙系数为G=0.4,可以看出,内柱半径的大小对作用在双筒柱上的最大波浪力的影响并不显著,而只对总波浪力的衰减区的位置有影响。对于较细内柱的双筒柱,衰减区位于较高频率。图9为作用在具有不同尺寸内柱的B柱上的总波浪力。对于这种形式的圆柱,内柱半径的大小对最大波浪力的影响也不显著,随内柱半径得减小,衰减区的位置也深移至较高频区。第10期膏
《图6》

图6 双筒柱A上总波浪力随波数Aa的分布
Fig.6 Total wave force on cylinder A
《图7》

图7 双筒柱B上总波浪力随波数版的分布
Fig. 7 Total wave force on cylinder B
《图8》

图8 带不同内柱的双筒柱A上总波浪力 随波数ka的分布
Fig.8 Total wave force on cylinder A at G = 0.4
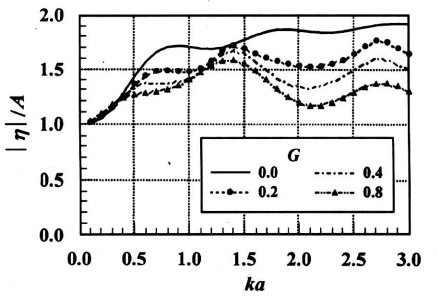
图10和图11是波浪在双筒柱A、B迎浪端的爬高随波数的分布,圆柱的儿何条件与图4和图5相同,孔隙系数的形式为G=Gx。波浪爬高随波数的变化而波动,B柱外的波面高度随外壁孔隙系数的增加而减小,A柱外的波浪爬高在谷值范围内下降很剧烈,而在峰值范围内,透空圆柱外的波浪爬高要比实体圆柱为大。
《图9》

图9 带不同内柱的双筒柱B上总波浪力 随波数ka的分布
Fig.9 Total wave force on cylinder B at G = 0.4
《图10》

图10双筒柱A迎浪端波浪爬高 随波数ka的分布
Fig. 10 Wave run-up at the wave-side of cylinder A
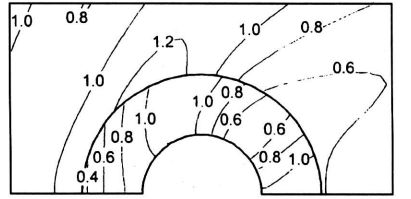
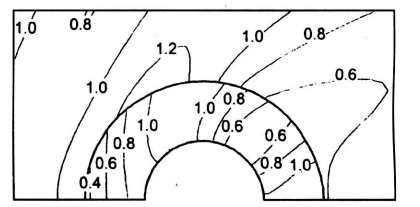
图12和图13是A柱和B柱周围波高的等值分布线,株柱特性与图10和图11中的相同,波数为ka=1.4,即对应于迎浪端波高很大的频率。从图中可以看到,在这一频率下,A柱迎浪端和桂柱内部的波高明显大于B柱的对应波高,在A柱内部,最大波高可达到入射波高的2.6倍。
图14和图15是波数为ka=2.2下,上述圆柱周围波高的等值分布线,即对应与迎浪端波高较小
《图11》

图11 双筒柱B迎浪端波浪爬高 随波数ka的分布
Fig. 11 Wave run-up at the wave-side of cylinder B at b/a =0.5 and G = GR
《图12》

图12 波数h=1.4下波浪对双筒柱A绕射 的波高等高线
Fig. 12 . The contour of wave elevation around cylinder A at ka = 1.4, b/a =0.5, G = 0.4
《图13》

图13 波数版=1.4下波浪对双筒柱 B绕射的波高等高线
Fig. 13 The contour of wave elevation around cylinder B at 左a = 1.4, b/a =0.5, G = 0.4
的频率。从图中可以看到,在这一频率下,A柱外部的波浪高度与B柱外的波高基本相同,而A柱内的波高可达到入射波的1.4借,而B柱内的波高仅为1.0倍。
《图14》

图14 波数Aa = 2.2下波浪对双筒柱 B绕射的波高等高线
Fig. 14 The contour of wave elevation around cylinder B at ka =2.2, b/a =0.5, G = 0.4
《图15 》

图15 波数版= 2.2下波浪对双筒柱 B绕射的波高等高线
Fig. 15 The contour of wave elevation around cylinder B at ka= 2.2, b/a =0.5, G = 0.4
《6 结语》
6 结语
本文建立了波浪关于透空外壁双筒柱绕射的解析解,通过数值研究可得到以下结论:
1) 对于全透空外壁双筒柱,在整个频率范图内,波浪力随孔隙系数的增加而显著减小。对于半透空外壁双筒柱,在较低频率下,孔隙系数对作用在外壁和整个圆柱上的波浪荷载影响并不显著,在较高频率下,波浪力随孔隙系数的增加而迅速减小。
2) 双筒柱外波浪爬高随波浪频率而上下波动。对于外壁全透空的双筒柱,在整个波浪频率范图内,波浪高度随外壁孔隘系数的增加而减小。对于外壁半透空的双筒柱,波面高度的波动幅值比全透空圆柱要大。在一定波浪频率范围内,半透空外壁双筒柱外的波面高度比全透空外壁双筒柱外的波面高度低;在其它一些频率范围内,半透空外壁双筒柱外波面高度要比相当的实体圆柱外波高还要大;在半透空外壁双筒柱内部波浪高度可达到入射波高的2.6倍。



















 京公网安备 11010502051620号
京公网安备 11010502051620号




