《1 引言 　 》

1 引言 　 　

通常区间数只用上下限来表示，有时称为两参数区间。在两参数区间数中，上、下限间的各个数值可以认为取值机会均等。用两参数区间数表示一个参量时，有时为了覆盖整个取值范围，区间可能会取得过大，这时如果再认为整个区间内取值机会均等，得出的结果就会出现大的误差。为了解决这个问题，使用三参数区间数进行决策，不仅保持了参数的取值区间，而且还能突出取值可能性最大的重心（即在区间内取值可能性最大的那个数），以弥补两参数区间数的不足。笔者在引用参考文献 [1 ~ 3]的一些定义的基础上，引入了三参数区间数，讨论了三参数区间数的性质、运算关系及排序指标等。最后根据逼近理想点法，提出了关于多指标决策问题的三参数区间数逼近理想点法，并予以实际应用。

《2 三参数区间数》

2 三参数区间数

《2.1 三参数区间数基本定义》

2.1 三参数区间数基本定义

定义 1   三参数区间数是用三个参数来表示一个区间数，记为 α＝且 ，其中 分别表示区间数取值的上限、下限，称为区间数的上限、下限； 表示在此区间中取值可能性最大的数，称为区间数的重心或理想值[3] 。

在三参数区间数中，重心 的取值机会最大，由 向上限或向下限取值可能性递减。对于区间数可以用分布函数的形式表示其在区间取值机会的大小，如图１所示[3] 。

《图 1》

图 1 三参数区间数

Fig.1 Interval numbers of three parameters

三参数区间数

若 时，称 α 为正三参数区间数；若 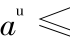０时，称 α 为负三参数区间数。特别是当 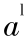＝ ＝ 时，三参数区间数 α 退化为普通实数。

定义 2 　设有两个灰色模糊数 C 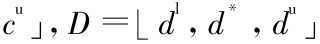＝，且它们的分布函数分别为 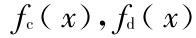，则

当 同时成立时，称 C 与 D 相等，记为C ＝ D 。

设 ，当 ＞０.５时，认为 C 大于 D ；当 ＝ 0.5 时，认为 C 等价于 D [3] 。

设 ，当 ＜ 0.5 时，认为 D 大于 C [3] 。

《2.2 三参数区间数运算关系》

2.2 三参数区间数运算关系

设有两个三参数区间数 α＝，，则

加法运算＋＝；

减法运算 - ＝

乘法运算 • ＝

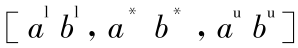
除法运算/ ＝

倍数运算

当 k 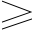０ 时 ，

当 k < ０ 时，

极值运算

指数运算 ，c 为正实数；

方次运算 = 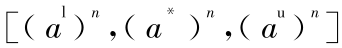，0 ，n 为正实数；

距离运算

范数运算

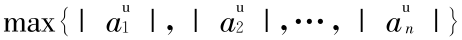设 是任意三参数区间数列向量，则称= 为 X 的范数。

《3 三参数区间数的逼近理想点法》

3 三参数区间数的逼近理想点法

《3.1 建立标准决策矩阵》

3.1 建立标准决策矩阵

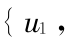
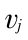对于多目标决策问题，设备择集 U ＝ ，因素集 V ＝。因素集中 的权重 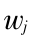不能完全确定，但却知 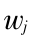∈ 且趋向于 。其中  ， j ＝ 1 ，2 ，…， n ，且 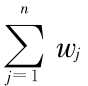=１。根据某个因素给出评判对象对备择集中各元素的隶属度，用三参数区间数表示的决策矩阵为 A 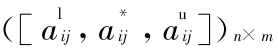＝，其中，（ i ＝ 1 ，2 ，…，n ；j ＝ 1 ，2 ，…，m）为备择 对因素 的属性值。

由于各指标的含义不同，指标值的计算方法也不同，造成各个指标的量纲各异，因此为了使各指标有公度性，必须对决策矩阵进行标准化处理。令 J＋＝｛效益型指标｝，J -＝｛成本型指标｝，J fixed ＝｛固定型指标｝。则将决策矩阵 A ＝ 标准化处理，令

效益型指标：

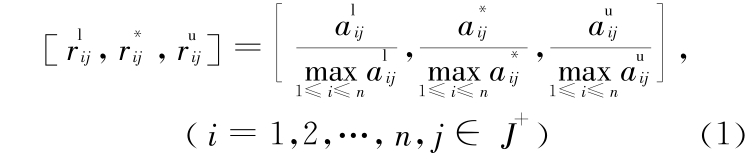
成本型指标：

固定型指标：

式中  ；，（ i ＝1 ，2 ，… ，n ；j ＝ 1 ，2 ，… ，m） ，且 为固定值。

所以标准化决策矩阵

即

《3.2 确定权重向量》

3.2 确定权重向量

权重向量表示的是各影响因素在评判过程中所占的重要性程度，为了减少决策中的主观因素，用标准差法确定权重向量[4 ,5] 。用三参数区间数的形式表示为

归一化处理得到规范化权重：

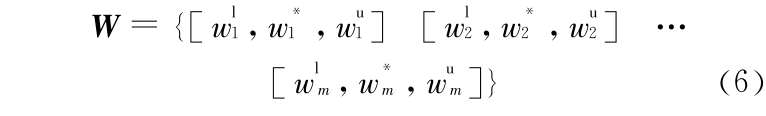
其中 ,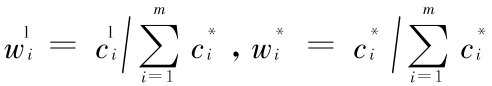

《3.3 三参数区间数的加权标准决策矩阵》

3.3 三参数区间数的加权标准决策矩阵

三参数区间数的加权标准决策矩阵为

其中

《3.4 定义理想方案 A + 和负理想方案 A -》

3.4 定义理想方案 A + 和负理想方案 A -

令正理想方案：

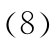
其中

负理想方案：

其中

《3.5 计算距离和相对贴近度》

3.5 计算距离和相对贴近度

令方案 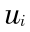（ i ＝ 1 ，2 ，…，n）到正理想方案的距离为 ，到负理想方案的距离为 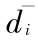，则

其中

其中 。

定义方案 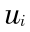（ i ＝ 1 ，2 ，…，n）到正理想方案的贴近度为 ，则 0 ＜ ＜ 1 。按 （ i ＝ 1 ，2 ，…，n）由大到小的次序排列，其中值最大的对应的方案最优。

《4 应用举例 》

4 应用举例 　 　

2005 年根据某市现有公交线路网络，考虑到城市的发展，有关部门提出 5 种公交线网的优化调整方案，要求有关部门在这 5 种方案中选出一种最佳的优化方案。其中考察的指标有：乘客出行时间、线网覆盖率、乘客直达率、线网重复系数和线网日均满载率[6 ,7] 。 5 种优化方案记为方案 1 、方案 2 、方案 3 、方案 4 和方案 5 。各方案对指标的考察值如表 1 所示。

《表 1》

表 1 指标考察值

Table 1 The observe values of indexes

表中数据由交通规划部门提供

步骤 1 　建立决策矩阵

。

步骤 2 　决策矩阵标准化处理

。

步骤 3 　由式（5）知权重向量

。

由式（6）归一化：

。

步骤 4 　由式（7）三参数区间数的加权标准决策矩阵

。

步骤 5 　于是由式（8）、式（9）知：

正理想方案 A +＝{ [0.15 ,0.17 ,0.19]  [0.18 ,0.21 ,0.22]  [0 ,0 ,0]  [0.19 ,0.22 ,0.25]  [0 ,0 ,0] } ;

负理想方案 A -＝｛[0 ,0 ,0]  [0 ,0 ,0]  [0.14 ,0.16 ,0.19]  [0 ,0 ,0]  [0.21 ,0.22 ,0.27]｝ 。

步骤 6   由式（10）、式（11）知：

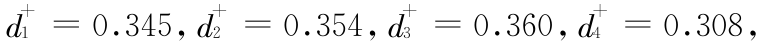
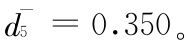
所以贴近度 e1 = 0.496 ，e2 = 0.463 ， e3 = 0.492 ，e4 = 0.498 , e5 = 0.534 ，即：

1 > e5 > e4 > e1 > e3 > e2 > 0 ，方案 5 为最佳方案。

《5 结语 》

5 结语 　 　

1）笔者利用区间数的知识，探讨了三参数区间数的定义及运算关系，然后结合逼近理想点法提出了三参数区间数的逼近理想点法。目前对区间数多指标决策问题的研究已经引起广泛的重视[1 ~ 5] ，其研究方法有两类：主观类和客观类。主观类优缺点：解释性较强，但客观性较差；客观类优缺点：客观性较强，但解释性较差，甚至与实际情况相悖。在引入三参数区间数的情况下，给出了区间数多指标决策的一种新方法。该法以逼近理想点法和标准差法为依据，建立了区间数多指标决策的数学模型，并给出了模型的精确解。最后通过实例说明了此方法的合理性。

2）笔者在定义三参数区间数运算关系的基础上，对三参数区间数多指标决策问题的决策矩阵进行规范化处理，将三参数区间数多指标问题转化为指标取值为三参数区间数的多指标决策问题，然后在用标准差法确定权重向量的情况下，建立了三参数区间数的逼近理想点法。在实际应用中，该方法简单实用、所需信息少。与其他方法（如灰色决策法 [2] 、模糊决策法[3] 等）相比较，主观性小，计算过程科学合理，适用性强。

3）借助逼近理想点给出的三参数区间数的逼近理想点法，既适用于区间数多指标决策问题，又适合于指标取值为区间数的多指标问题，具有广泛的实用性。国内外对区间数及排序方法的研究比较多，对三参数区间数的研究比较少。关于三参数区间数的运算关系及排序方法目前还没有一种能够被普遍接受，尚需做进一步的探讨和研究。